Normal Modes
- Page ID
- 1856
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Normal modes are used to describe the different vibrational motions in molecules. Each mode can be characterized by a different type of motion and each mode has a certain symmetry associated with it. Group theory is a useful tool in order to determine what symmetries the normal modes contain and predict if these modes are IR and/or Raman active. Consequently, IR and Raman spectroscopy is often used for vibrational spectra.
Overview of Normal Modes
In general, a normal mode is an independent motion of atoms in a molecule that occurs without causing movement to any of the other modes. Normal modes, as implied by their name, are orthogonal to each other. In order to discuss the quantum-mechanical equations that govern molecular vibrations it is convenient to convert Cartesian coordinates into so called normal coordinates. Vibrations in polyatomic molecules are represented by these normal coordinates.
There exists an important fact about normal coordinates. Each of these coordinates belongs to an irreducible representation of the point the molecule under investigation. Vibrational wavefunctions associated with vibrational energy levels share this property as well. The normal coordinates and the vibration wavefunction can be categorized further according to the point group they belong to. From the character table predictions can be made for which symmetries can exist. The irreducible representation offers insight into the IR and/or Raman activity of the molecule in question.
Degrees of Freedom
3N where N represents the number of nuclei present in the molecule is the total number of coordinates needed to describe the location of a molecule in 3D-space. 3N is most often referred to as the total number of degrees of freedom of the molecule being investigated. The total number of degrees of freedom, can be divided into:
- 3 coordinates to describe the translational motion around the center of mass; these coordinates are called the translational degrees of freedom
- 3 coordinates to describe the rotational motion in non-linear molecules; for linear molecules only 2 coordinates are required; these coordinates are called the rotational degrees of freedom
- the remaining coordinates are used to describe vibrational motion; a non-linear molecule has 3N - 6 vibrational degrees of freedom whereas a linear molecule has 3N -5 degrees of freedom.
| Total Degree of Freedom | Translational degrees of freedom | Rotational degrees of freedom | Vibrational degrees of freedom | |
|---|---|---|---|---|
| Nonlinear Molecules | 3N | 3 | 3 | 3N -6 |
| Linear Molecules | 3N | 3 | 2 | 3N - 5 |
Ethane, \(C_2H_6\) has eight atoms (\N=8\) and is a nonlinear molecule so of the \(3N=24\) degrees of freedom, three are translational and three are rotational. The remaining 18 degrees of freedom are internal (vibrational). This is consistent with:
\[3N -6 =3(8)-6=18\]
Carbon Dioxide, \(CO_2\) has three atoms (\(N=3\) and is a linear molecule so of the \(3N=9\) degrees of freedom, three are translational and two are rotational. The remaining 4 degrees of freedom are vibrational. This is consistent with:
\[3N - 5 = 3(3)-5 = 4\]
Mathematical Introduction to Normal Modes
If there is no external field present, the energy of a molecule does not depend on its orientation in space (its translational degrees of freedom) nor its center of mass (its rotational degrees of freedom). The potential energy of the molecule is therefore made up of its vibrational degrees of freedom only of \(3N-6\) (or \(3N-5\) for linear molecules).
The difference in potential energy is given by:
\[\begin{align} \Delta V &= V(q_1,q_2,q_3,...,q_n) - V(0,0,0,...,0) \tag{1} \\[4pt] &= \dfrac{1}{2} \sum_{i=1}^{N_{vib}} \sum_{j=1}^{N_{vib}} \left(\dfrac{\partial^2 V}{\partial q_i\partial q_j} \right) q_iq_j \tag{2} \\[4pt] &= \dfrac{1}{2}\sum_{i=1}^{N_{vib}} \sum_{j=1}^{N_{vib}} f_{ij} q_iq_j \tag{3} \end{align}\]
where
- \(q\) represents the equilibrium displacement and
- \(N_{vib}\) the number of vibrational degrees of freedom.
For simplicity, the anharmonic terms are neglected in this equation (consequently there are no higher order terms present). A theorem of classical mechanics states that the cross terms can be eliminated from the above equation (the details of the theorem are very complex and will not be discussed in detail). By using matrix algebra a new set of coordinates {Qj} can be found such that
\[\Delta{V} = \dfrac{1}{2} \sum_{j=1}^{N_{vib}}{F_jQ_j^2} \tag{4}\]
Note that there are no cross terms in this new expression. These new coordinates are called normal coordinates or normal modes. With these new normal coordinates in hand, the Hamiltonian operator for vibrations can be written as follows:
\[\hat{H}_{vib} = -\sum_{j=1}^{N_{vib}} \dfrac{\hbar^2}{2\mu_i} \dfrac{d^2}{dQ_j^2} + \dfrac{1}{2} \sum_{j=1}^{N_{vib}}F_jQ_j^2 \tag{5}\]
The total wavefunction is a product of the individual wavefunctions and the energy is the sum of independent energies. This leads to:
\[ \hat{H}_{vib} = \sum_{j=1}^{N_{vib}} \hat{H}_{vib,j} = \sum_{j=1}^{N_{vib}} \left( \dfrac{-\hbar^2}{2 \mu_j}\dfrac{d^2}{dQ_i^2} + \dfrac{1}{2}\sum_{j=1}^{N_{vib}} F_jQ_j^2 \right) \tag{6}\]
and the wavefunction is then
\[ \psi_{vib} = Q_1,Q_2, Q_3 ..., Q_{vib} = \psi_{vib,1}(Q_1) \psi_{vib,2}(Q_2) \psi_{vib,3}(Q_3) , ..., \psi_{vib,N_{vib}}(Q_{N_{vib}}) \tag{7}\]
and the total vibrational energy of the molecule is
\[E_{vib} = \sum_{j=1}^{N_{vin}} h\nu_j \left (v_j + \dfrac{1}{2}\right) \tag{8}\]
where \(v_j= 0,1,2,3...\)
The consequence of the result stated in the above equations is that each vibrational mode can be treated as a harmonic oscillator approximation. There are \(N_{vib}\) harmonic oscillators corresponding to the total number of vibrational modes present in the molecule.
In the ground vibrational state the energy of the molecule is equal to (1/2)hνj. The ground state energy is referred to as zero point energy. A vibration transition in a molecule is induced when it absorbs a quantum of energy according to E = hv. The first excited state is separated from the ground state by Evib = (3/2)hν since vj = 1, the next energy level separation is (5/2)hν, etc...
The harmonic oscillator is a good approximation, but it does not take into account that the molecule, once it has absorbed enough energy to break the vibrating bond, does dissociate. A better approximation is the Morse potential which takes into account anharmonicity. The Morse potential also accounts for bond dissociation as well as energy levels getting closer together at higher energies.
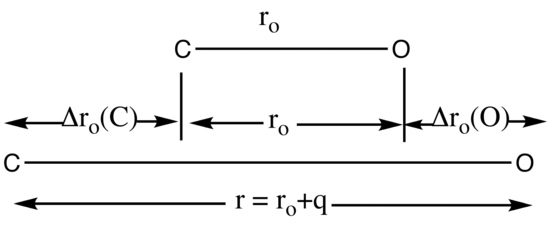
Pictorial description of normal coordinates using CO
The normal coordinate q is used to follow the path of a normal mode of vibration. As shown in Figure 2 the displacement of the C atom, denoted by Δro(C), and the displacement of the O atom, denoted by Δro(O), occur at the same frequency. The displacement of atoms is measured from the equilibrium distance in ground vibrational state, ro.
Description of vibrations
- ν = stretching is a change in bond length; note that the number of stretching modes is equal to the number of bonds on the molecule
- δ = bending is a change in bond angle
- ρr = rocking is change in angle between a group of atoms
- ρw = wagging is change in angle between the plane of a group of atoms
- ρt = twisting is change in angle between the planes of two groups of atoms
- π= out of plane
In direct correlation with symmetry, subscripts s (symmetric), as (asymmetric) and d (degenerate) are used to further describe the different modes.
A normal mode corresponding to an asymmetric stretch can be best described by a harmonic oscillator: As one bond lengthens, the other bond shortens. A normal mode that corresponds can be best described by a Morse potential well: As the bond length increases the potential energy increases and levels off as the bond length gets further away from the equilibrium.
The use of Symmetry and Group Theory
Symmetry of normal modes
It is important to realize that every normal mode has a certain type of symmetry associated with it. Identifying the point group of the molecule is therefore an important step. With this in mind it is not surprising that every normal mode forms a basis set for an irreducible representation of the point group the molecule belongs to. For a molecule such as water, having a structure of XY2, three normal coordinates can be determined. The two stretching modes are equivalent in symmetry and energy. The figure below shows the three normal modes for the water molecule:
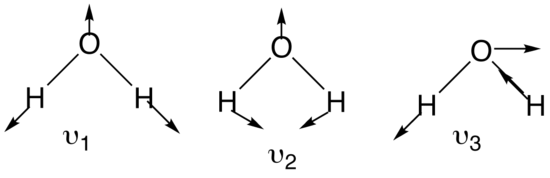
Figure 3: Three normal modes of water
By convention, with nonlinear molecules, the symmetric stretch is denoted v1 whereas the asymmetric stretch is denoted v2. Bending motions are v3. With linear molecules, the bending motion is v2 whereas asymmetric stretch is v3.
The water molecule has C2v symmetry and its symmetry elements are E, C2, σ(xz) and σ(yz). In order to determine the symmetries of the three vibrations and how they each transform, symmetry operations will be performed.
As an example, performing C2 operations using the two normal mode v2 and v3 gives the following transformation:

Once all the symmetry operations have been performed in a systematic manner for each modes the symmetry can be assigned to the normal mode using the character table for C2v:
| C2v | E | C2 | σ (xz) | σ (yz) | |
|---|---|---|---|---|---|
| ν1 | 1 | 1 | 1 | 1 | = a1 |
| ν2 | 1 | 1 | 1 | 1 | = a1 |
| ν3 | 1 | -1 | -1 | 1 | = b2 |
Water has three normal modes that can be grouped together as the reducible representation
\[Γ_{vib}= 2a_1 + b_2.\]
Determination of normal modes becomes quite complex as the number of atoms in the molecule increases. Nowadays, computer programs that simulate molecular vibrations can be used to perform these calculations.
The example of [PtCl4]2- shows the increasing complexity. The molecule has five atoms and therefore 15 degrees of freedom, 9 of these are vibrational degrees of freedom. The nine normal modes are exemplified below along with the irreducible representation the normal mode belongs to (D4h point group).
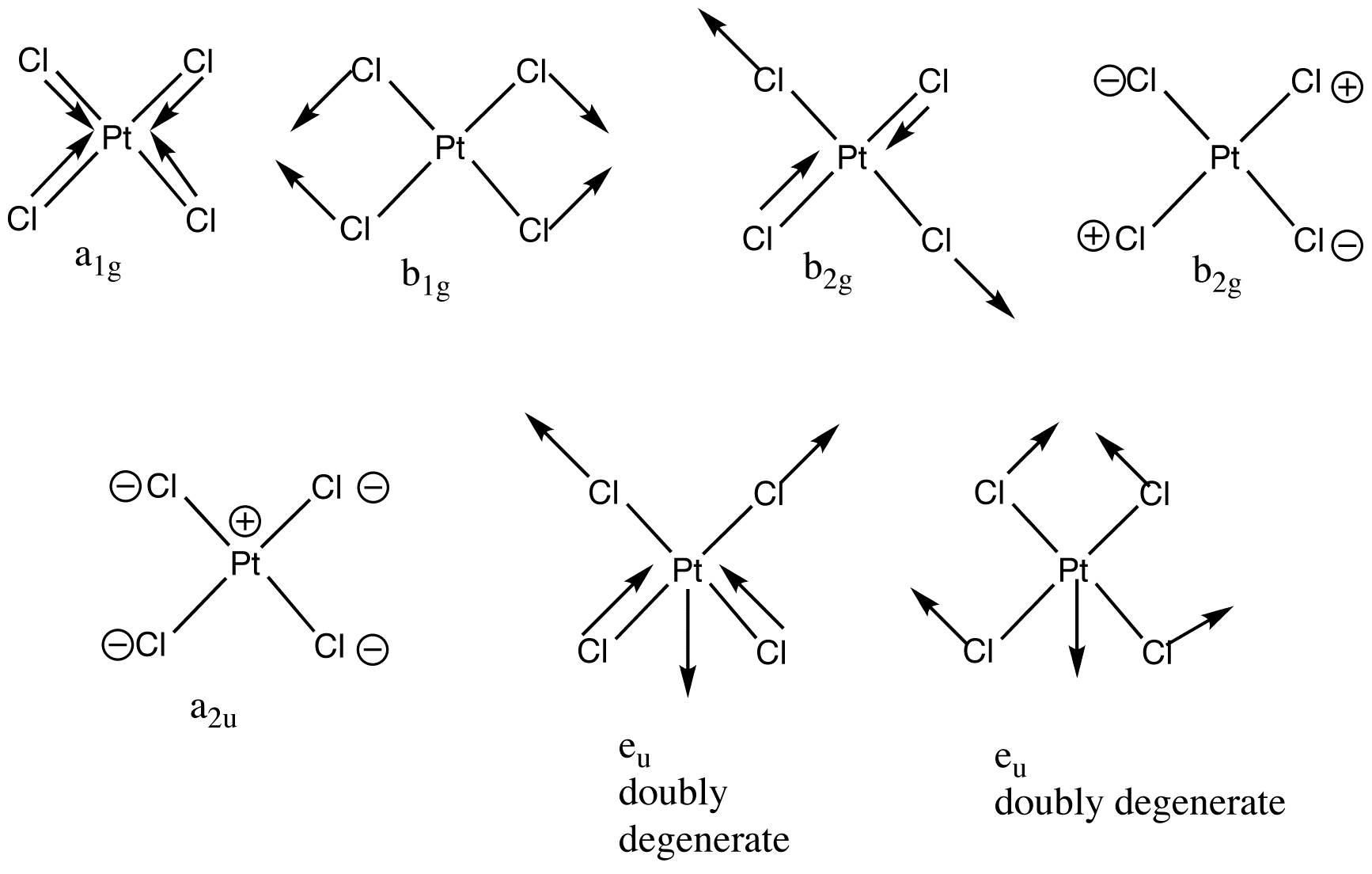
A1g, b1g and eu are stretching vibrations whereas b2g, a2u, b2u and eu are bending vibrations.
Determining if normal modes are IR and/or Raman active
Transition Moment Integral
A transition from \(\ce{v -> v'}\) is IR active if the transition moment integral contains the totally symmetric irreducible representation of the point group the molecule belongs to.
The transition moment integral is derived from the one-dimensional harmonic oscillator. Using the definition of dipole moment the integral is:
\[M\left(v \rightarrow v^{\prime}\right)=\int_{-\infty}^{\infty} \psi^{*}\left(v^{\prime}\right) \mu \psi(v) d x\]
If μ, the dipole moment, would be a constant and therefore independent of the vibration, it could be taken outside the integral. Since v and v' are mutually orthogonal to each other, the integral will equal zero and the transition will not be allowed. In order for the integral to be nonzero, μ must change during a vibration. This selection rule explains why homonuclear diatomic molecules do not produce an IR spectrum. There is no change in dipole moment resulting in a transition moment integral of zero and a transition that is forbidden.
For a transition to be Raman active the same rules apply. The transition moment integral must contain the totally symmetric irreducible representation of the point group. The integral contains the polarizability tensor (usually represented by a square matrix):
\[M\left(v \rightarrow v^{\prime}\right)=\int_{-\infty}^{\infty} \psi^{*}\left(v^{\prime}\right) \alpha \psi(v) d x\]
\(α\) must be nonzero in order for the transition to be allowed and show Raman scattering.
Character Tables
For a molecule to be IR active the dipole moment has to change during the vibration. For a molecule to be Raman active the polarizability of the molecule has to change during the vibration. The reducible representation Γvib can also be found by determining the reducible representation of the 3N degrees of freedom of H2O, Γtot. By applying Group Theory it is straightforward to find Γx,y,z as well as UMA (number of unmoved atoms). Again, using water as an example with C2v symmetry where 3N = 9, Γtot can be determined:
| C2v | E | C2 | σ (xz) | σ (yz) | |
|---|---|---|---|---|---|
| Τx,y,z | 3 | -1 | 1 | 1 | |
| UMA | 3 | 1 | 1 | 3 | |
| Γtot | 9 | -1 | 1 | 3 | =3a1 + a2 + 2b1 + 3b2 |
|
Note that Γtot contains nine degrees of freedom consistent with 3N = 9. |
|||||
Γtot contains Γtranslational, Γrotational as well as Γvibrational. Γtrans can be obtained by finding the irreducible representations corresponding to x,y and z in the right side of the character table, Γrot by finding the ones corresponding to Rx, Ry and Rz. Γvib can be obtained by Γtot - Γtrans - Γrot.
Γvib (H2O) = (3a1 + a2 + 2b1+ 3b2) - (a1 + b1 + b2) - (a2 + b1 + b2) = 2a1 + b2
In order to determine which modes are IR active, a simple check of the irreducible representation that corresponds to x,y and z and a cross check with the reducible representation Γvib is necessary. If they contain the same irreducible representation, the mode is IR active.
For H2O, z transforms as a1, x as b1 and y as b2. The modes a1 and b2 are IR active since Γvib contains 2a1 + b2.
In order to determine which modes are Raman active, the irreducible representation that corresponds to z2, x2-y2, xy, xz and yz is used and again cross checked with Γvib. For H2O, z2 and x2-y2 transform as a1, xy as a2, xz as b1 and yz as b2.The modes a1 and b2 are also Raman active since Γvib contains both these modes.
The IR spectrum of H2O does indeed have three bands as predicted by Group Theory. The two symmetric stretches v1 and v2 occur at 3756 and 3657 cm-1 whereas the bending v3 motion occurs at 1595 cm-1.
In order to determine which normal modes are stretching vibrations and which one are bending vibrations, a stretching analysis can be performed. Then the stretching vibrations can be deducted from the total vibrations in order to obtain the bending vibrations. A double-headed arrow is drawn between the atom as depicted below:
Then a determination of how the arrows transform under each symmetry operation in C2v symmetry will yield the following results:
| C2v | E | C2 | σ (xz) | σ (yz) | |
|---|---|---|---|---|---|
| Γstretch | 2 | 0 | 0 | 2 | = a1 + b2 |
Γbend = Γvib - Γstretch = 2a1 + b2 -a1 - b2 = a1
H2O has two stretching vibrations as well as one bending vibration.
This concept can be expanded to complex molecules such as PtCl4-. Four double headed arrows can be drawn between the atoms of the molecule and determine how these transform in D4h symmetry. Once the irreducible representation for Γstretch has been worked out, Γbend can be determined by Γbend = Γvib - Γstretch.
Fundamental transition, overtones and hot bands
The transition from v=0 (ground state) -> v=1 (first excited state) is called the fundamental transition. This transition has the greatest intensity. The transition from v=0 --> v=2 is is referred to as the first overtone, from v=0 --> v=3 is called the second overtone, etc. Ovetones occur when a mode is excited above the v = 1 level. The harmonic oscillator approximation supports the prediction that the transition to a second overtone will be twice as energetic as a fundamental transition.
Most molecules are in their zero point energy at room temperature. Therefore, most transitions do originate from the v=0 state. Some molecules do have a significant population of the v=1 state at room temperature and transitions from this thermally excited state are called hot bands. Combination bands can occur if more than one vibration is excited by the absorption of a photon. The overall energy of a combination band is the result of the sum of individual transitions.
References
- Merlin, J.C., Cornard, J.P., J. Chem. Educ., 2006, 83 (9), p 1383. DOI: 10.1021/ed083p1393
- McGuinn, C.J., J. Chem. Educ., 1982, 59 (10), p 813. DOI: 10.1021/ed059p813
- Harris, D.C., Bertolucci, M.D., Symmetry and Spectroscopy: An introduction to Vibrational and Electronic Spectroscopy. Dover Publocations, Inc., New York, 1989.
- McQuarrie, D. A., Simon, J.D., Physical Chemistry: A Molecular Approach, University Science Books, Sausalito, California, 1997; 518-521.
- Housecroft, C.E., Sharpe, A.G., Inorganic Chemistry. Pearson Education Limited, England, 2008, 107.
- Atkins, P., dePaula, J., Physical Chemistry, W.H. Freeman and Company, New York, 2002, 520-523.
- Bishop, D.M., Group Theory and Chemistry, Dover Publications, Inc, New York, 1973, 166.
Problems
- Chlorophyll a is a green pigment that is found in plants. Its molecular formula is C55H77O5N4Mg. How many degrees of freedom does this molecule possess? How many vibrational degrees of freedom does it have?
- CCl4 was commonly used an as organic solvent until its severe carcinogenic properties were discovered. How many vibrational modes does CCl4 have? Are they IR and/or Raman active?
- The same vibrational modes in H2O are IR and Raman active. WF6- has IR active modes that are not Raman active and vice versa. Explain why this is the case.
- How many IR peaks do you expect from SO3? Estimate where these peaks are positioned in an IR spectrum.
- Calculate the symmetries of the normal coordinates of planar BF3.
Answers to Problems
- chlorophyll has 426 degrees of freedom, 420 vibrational modes
- The point group is Td, Tvib = a1 + e + 2t2, a1 and e are Raman active, t2 is both IR and Raman active
- For molecules that possess a center of inversion i, modes cannot be simultaneously IR and Raman active
- Point group is D3h, one would expect three IR active peaks. Asymmetric stretch highest (1391 cm-1), two bending modes (both around 500 cm-1). The symmetric stretch is IR inactive
- T3N = A1' + A2' + 3E' + 2 A2" + E" and Tvib= A1' + 2E' + A2"