Combination Bands, Overtones and Fermi Resonances
- Page ID
- 1853
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Combination bands, overtones, and Fermi resonances are used to help explain and assign peaks in vibrational spectra that do not correspond with known fundamental vibrations. Combination bands and overtones generally have lower intensities than the fundamentals, and Fermi resonance causes a spilt and shift in intensity of peaks with similar energies and identical symmetries. Hot bands will also be briefly addressed.
Introduction
Fundamental vibrational frequencies of a molecule corresponds to transition from v=0 to v=1. For a non-linear molecule there will by 3N-6 (where N is the number of atoms) number vibrations. The same holds true for linear molecules, however the equations 3N-5 is used, because a linear molecule has one less rotational degrees of freedom. (For a more detailed explanation see: Normal Modes). Figure 1 shows a diagram for a vibrating diatomic molecule. The levels denoted by vibrational quantum numbers v represent the potenital energy for the harmonic (quadratic) oscillator. The transition \( 0 \rightarrow 1 \) is fundamental, transitions \( 0 \rightarrow n \) (n>1) are called overtones, and transitions \( 1 \rightarrow n\) (n>1) are called hot transitions (hot bands).
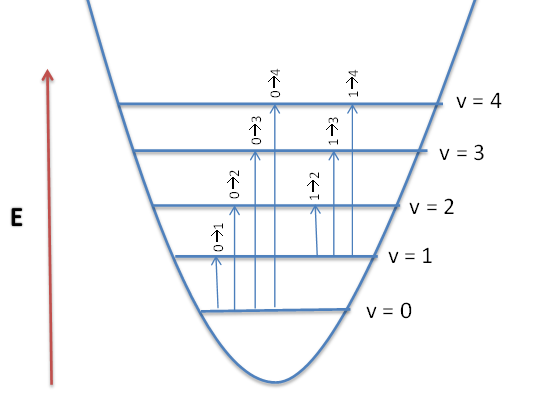
Symmetry Requirements
The symmetry requirement of vibrational transisition is given by the transition moment integral,
\[ \mu =\int \psi ^{\ast } \boldsymbol{\mathbf{}\mu} \psi d\tau \neq 0 \]
where,
\[ \boldsymbol{\mu }=\textbf{i}\mu _{x}+\textbf{j}\mu _{y}+\textbf{k}\mu _{z} \]
These integrals can be separated into each component: x,y, and z. Because the ground state contains the totally symmetric representation, the coordinate x, y, or z and ψ* must belong to the same representation so that the direct product will contain the totally symmetric representation.
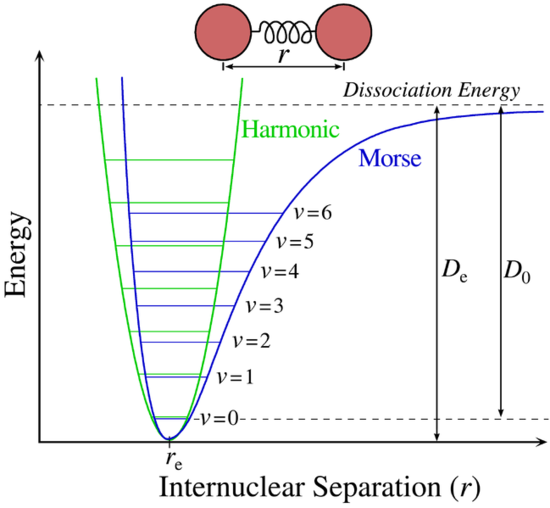
Harmonic Oscillator Breakdown
The harmonic oscillator approximation is convenient to use for diatomic molecules with quantized vibrational energy levels given by the following equation:
\[ E_{v}(cm^{-1}) = \left (v + \frac{1}{2} \right) \omega_{e} \]
A more accurate description of the vibrational energies is given by the anharmonic oscillator (also called Morse potential) with energy of
\[ E_{v}(cm^{-1}) = \omega_{e} \left (v + \frac{1}{2} \right) - \omega_{e}x_{e} \left (v + \frac{1}{2} \right)^2 + \omega_{e}y_{e} \left (v + \frac{1}{2} \right)^3 +...\]
where ωe is the vibrational frequency for the re internuclear separation and ωe >> ωexe >> ωeye. This accounts for the fact that as the higher vibrational states deviate from the perfectly parabolic shape, the level converge with increasing quantum numbers. It is because of this anharmoniticity that overtones can occur.
While it may seem that the harmonic oscillator and the anharomic oscillator are closely related, this is in fact not the case. The differences in the wavefunctions lead to a breakdown of selection rules, specifically, Δv=±1 selection rule can not be applied, and higher order terms must be accounted in the energy calculations.
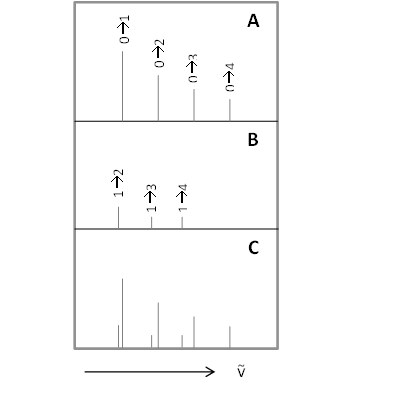
There is only a small correction from the ground state to the first excited state for the anharmonic correction, but it becomes much larger for more highly excited states which are populated as the temperature increases. The deviation from the harmonic oscillator to the anharmonic oscillator results in expanding the energy function with additional terms and treating these terms with perturbation theory. The results in the correct vibrational energies and also relaxes the selection rules. A Δv=±1 is still most predominant, however, weaker overtones with Δv=±2, ±3,… can occur. It should be noted that a Δv=2 transition does not occur at twice the frequency of the fundamental transition, but at a lower frequency. Overtone transitions are not always observed, especially in larger molecules, because the transitions become weaker with increasing Δv.
Overtones
Overtones occur when a vibrational mode is excited from \(v=0\) to \(v=2\), which is called the first overtone, or v=0 to v=3, the second overtone. The fundamental transitions, \(v=±1\), are the most commonly occurring, and the probability of overtones rapid decreases as the number of quanta (\(Δv=±n\)) increases. Based on the harmonic oscillator approximation, the energy of the overtone transition would be n times larger than the energy of the fundamental transition frequency, but the anharmonic oscillator calculations show that the overtones are less than a multiple of the fundamental frequency. This is demonstrated with the vibrations of the diatomic \(\ce{HCl}\) in the gas phase:
| Transition | Term | ṽobs [cm-1] | ṽHarmonic [cm-1] | ṽAnharmonic [cm-1] |
|---|---|---|---|---|
| \( 0 \rightarrow 1 \) | fundamental | 2,885.9 | 2,885.9 | 2,885.3 |
| \( 0 \rightarrow 2 \) | first overtone | 5,668.0 | 5,771.8 | 5,665.0 |
| \( 0 \rightarrow 3 \) | second overtone | 8,347.0 | 8,657.7 | 8,339.0 |
| \( 0 \rightarrow 4\) | third overtone | 10,923.1 | 11,543.6 | 10,907.4 |
| \( 0 \rightarrow 5\) | fourth overtone | 13,396.5 | 14,429.5 | 13,370 |
We can see from Table 1, that the anharmonic frequencies correspond much better with the observed frequencies, especially as the vibrational levels increase.
Special case
If one of the symmetries is doubly degenerate in the excited state, a recursion formula is required to determine the symmetry of the vth wave function, given by,
\[ \chi _{v}(R) = \frac{1}{2} \left [\chi (R) \chi_{v-1}(R) + \chi (R^{v}) \right] \]
Where χv(R) is the character under the operation R for the vth energy level; χ(R) is the character under R for the degenerate irreducible representation; χv-1(R) is the character of the (v-1)th energy level; and χ(Rv) is the character of the operation Rv. This is demonstrated for the D3h point group below.
Combination Bands
Combination bands are observed when more than two or more fundamental vibrations are excited simultaneously. One reason a combination band might occur is if a fundamental vibration does not occur because of symmetry. This is comparable to vibronic coupling in electronic transitions in which a fundamental mode can be excited and allowed as a “doubly excited state.” Combination implies addition of two frequencies, but it also possible to have a difference band where the frequencies are subtracted.
To determine if two states can be excited simultaneous the transition moment integral must be evaluated with the appropriate excited state wavefunction. For example, in the transition,
\[ \psi ^{_{1}}\left( 0 \right )\psi ^{_{2}}\left ( 0 \right )\psi ^{_{3}}\left ( 0 \right )\rightarrow \psi ^{_{1}}\left ( 2 \right )\psi ^{_{2}}\left ( 0 \right )\psi ^{_{3}}\left ( 1 \right ) \]
the symmetry of the excited state will be the direct product of the irreducible representation for ψ1(2) and ψ3(1).
For example, in the point group C4v, v1 has symmetry e and v3 has symmetry a2. By performing the calculations listed above, it is determined that ψ1(2) has (a1 + b1 + b2) symmetry:
\[ \Gamma [\psi_{es}] = \Gamma [\psi _{1}(2)] \otimes \Gamma [\psi _{3}(1)] = (a_{1} + b_{1} + b_{2})\times a_{2} = a_{2} + b_{2} + b_{1} \]
A practical use for understanding overtones and combination bands is applied to organic solvents used in spectroscopy. Most organic liquids have strong overtone and combination bands in the mid-infrared region, therefore, acetone, DMSO, or acetonitrile should only be used in very narrow spectral regions. Solvents such at CCl4, CS2 and CDCl3 can be used above 1200 cm-1.
Hot Bands
Hot bands are observed when an already excited vibration is further excited. For example an v1 to v1' transition corresponds to a hot band in its IR spectrum. These transitions are temperature dependent, with lower signal intensity at lower temperature, and higher signal intensity at higher temperature. This is because at room temperature only the ground state is highly populated (kT ~ 200 cm-1), based on the Boltzmann distribution. The Maxwell-Boltzmann distribution law states that if molecules in thermal equilibrium occupy two states of energy εj and εi, the relative populations of molecules occupying these states will be,
\[ \large \dfrac{n_{j}}{n_{i}}=\dfrac{e^{-\varepsilon _{j}/RT}}{e^{-\varepsilon _{i}/RT}}=e^{-\Delta \varepsilon /RT} \]
where, k is the Boltzmann constant and T is the temperature in Kelvin.
In the harmonic oscillator model, hot bands are not easily distinguished from fundamental transitions because the energy levels are equally spaced. Because the spacing between energy levels in the anharmonic oscillator decrease with increasing vibrational levels, the hot bands occur at lower frequencies than the fundamentals. Also, the transition moment integrals are slightly different since the ground state will not necessarily be totally symmetric since it is not in v=0.
\[ \psi ^{_{1}} \left( 0 \right )\psi ^{_{2}}\left ( 0 \right )\psi ^{_{3}}\left ( 1 \right )\rightarrow \psi ^{_{1}}\left ( 0 \right )\psi ^{_{2}}\left ( 0 \right )\psi ^{_{3}}\left ( 2 \right ) \]
Fermi Resonances
Fermi resonance results in the splitting of two vibrational bands that have nearly the same energy and symmetry in both IR and Raman spectroscopies. The two bands are usually a fundamental vibration and either an overtone or combination band. The wavefunctions for the two resonant vibrations mix according to the harmonic oscillator approximation, and the result is a shift in frequency and a change in intensity in the spectrum. As a result, two strong bands are observed in the spectrum, instead of the expected strong and weak bands. It is not possible to determine the contribution from each vibration because of the resulting mixed wave function.
If the symmetry requirements are fulfilled and the energies of the two states are similar, mixing occurs, and the resulting modes can be described by a linear combination of the two interacting modes. The effect of this interaction is to increase the splitting between the engery levels. The splitting will be larger if the original energy difference is small and the coupling energy is large. The mixing of the two states also equalized the intensities of the vibrations which allows a weak overtone or combination band to show significant intensity from the fundamental with which it has Fermi resonance with.
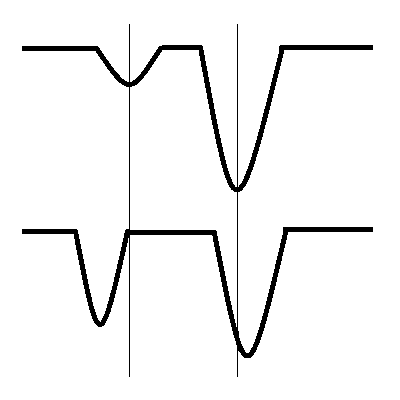
Because the vibrations have nearly the same frequency, the interaction will be affected if one mode undergoes a frequency shift from deuteration or a solvent effect while the other does not.The molecule most studied for this type of resonance (even what Fermi himself used to explain this phenomena), is carbon dioxide, CO2. The three fundamental vibrations are v1= 1337 cm-1, v2=667 cm-1, v3=2349 cm-1. The first overtone of v2 is v1 + 2v2 with symmetries σg+ and (σg+ + δg+), respectively, and frequencies of 1337 cm-1 (v1) and 2(667) = 1334 cm-1 (v2). According to group theory calculations, CO2 belongs to the point group D∞h and should only have one Raman (symmetric stretching vibrations) and two IR active modes (asymmetric stretching and bending vibrations). CS2 is an analog to this system.
Another typical example of Fermi resonance is found in the vibrational spectra of aldehydes, where the C-H bond in the CHO group interacts with the second harmonic level, 2δ(CHO), derived from the fundamental frequency of the deformation vibration of the CHO group (2*1400 cm-1). The result is a Fermi doublet with branches around 2830 and 2730 cm-1. It is important for Fermi resonance that the vibrations connected with the two interacting levels be localized in the same part of the molecule.
When bands have non-negligible widths, Fermi resonance perturbation of localized levels cannot be applied. This broadening can be the result of a number of things, such as, intermolecular interaction, shortened excited state lifetimes, or interaction of vibrational modes with phonons. In place of perturbation theory, the distribution of interacting vibrational states can be approximated as a collection of discrete level. The influence from each level can be calculated.
It is useful to understand Fermi resonance because it helps assign and identify peaks within vibrational spectra (ie. IR and Raman) that may not otherwise be accounted for, however it should not be used lightly when assigning spectra.It is easy to jump to the conclusion that an unidentifiable band is the result of Fermi resonance, however this explanation may not fully account for the inconsistency and further characterization may be required for the system being investigated. It is important to assign spectra before doing the normal mode (coordinate) calculations because doing these calculations beforehand often leads to incorrect assignments of the peaks in the spectra.
References
- Atkins, P. W. Molecular Quantum Mechanics. Oxford University Press, 1970.
- Guillory, William. Introduction to Molecular Structure and Spectroscopy. Boston, MA: Allyn & Bacon, Inc. , 1977.
- Struve, Walter. Fundamentals of Molecular Spectroscopy. Wiley, 1989.
- Harris, Daniel, and Michael Bertolucci. Symmetry and Spectroscopy . Oxford University Press, 1978.
- Cotton, F. Albert. Chemical Applications of Group Theory . 3rd. Wiley, 1990.
- Horak, M., and Antonin Vitek. Interpretations and Processing of Vibrational Specta. Wiley, 1978.
- Diem, M. Introduction to Modern Vibrational Spectroscopy. Wiley, 1993.
- Kondratyuk, P. "Analytical Formulas for Fermi Resonance Interactions in Continuous Distributions of States." Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy 61.4 (2005): 589-93. Web.
Problems
Q1. Given ν1 = 1151 cm-1, ν2 = 1361 cm-1, ν3 = 519 cm-1 for SO2, and the fact that there are 4 overtones and/or combination bands, predict the vibrational spectra and calculations.
A1.
| v [cm-1] | Assignment |
|---|---|
| 519 | v2 |
| 606 | ν1 - v2 |
| 1151 | v1 |
| 1361 | v3 |
| 1871 | v2 + v3 |
| 2305 | 2v1 |
| 2499 | v1 + v3 |
Q2. What are the two main effects of Fermi resonance?
A2. An overtone band can gain intensity from a nearby fundamental frequency with similiar symmetry. The energy levels of both bands are shifted away from one another.
Q3. Explain the difference between a combination band and an overtone.
An overtone is the result of Δv>1 from the ground state. A combination band is the result of a 2 fundamental frequencies being excited simultaneously so that the excitation is allowed by symmetry. The overtone is not subject to a symmetry requirement.
Q4. Why are hot bands temperature dependent?
A4. For a hot band to occur, a state other than the ground state must already be populated, and this requires >200cm-1 to over come the thermal energy of kT (Boltzmann constant times temperature). The more heat that it put into the system, the more likely a hot band is to occur, and the stronger the signal it will produce.
Q5. Show the calculations for the values in Figure 1 for both the harmonic and anharmonic oscillators.
A5. Equations to use: ṽ = 2885.90v, for harmonic and ṽ = 2990.9v – 52.82v(v+1) for anharmonic.
For v=3, ṽH = 2885.90(3) = 8657.7 ṽAH = 2990.9(3) – 52.82(3)(3+1) = 8339.0

