Number of Vibrational Modes in a Molecule
- Page ID
- 1857
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Heisenberg uncertainty principle argues that all atoms in a molecule are constantly in motion (otherwise we would know position and momentum accurately). For molecules, they exhibit three general types of motions: translations (external), rotations (internal) and vibrations (internal). A diatomic molecule contains only a single motion., while polyatomic molecules exhibit more complex vibrations, known as normal modes.
Molecular Vibrations
A molecule has translational and rotational motion as a whole while each atom has it's own motion. The vibrational modes can be IR or Raman active. For a mode to be observed in the IR spectrum, changes must occur in the permanent dipole (i.e. not diatomic molecules). Diatomic molecules are observed in the Raman spectra but not in the IR spectra. This is due to the fact that diatomic molecules have one band and no permanent dipole, and therefore one single vibration. An example of this would be \(\ce{O2}\) or \(\ce{N2}\). However, unsymmetric diatomic molecules (i.e. \(\ce{CN}\)) do absorb in the IR spectra. Polyatomic molecules undergo more complex vibrations that can be summed or resolved into normal modes of vibration.
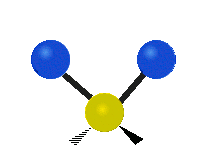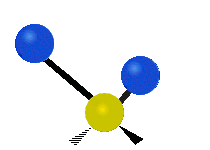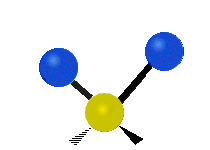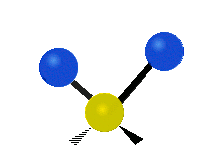
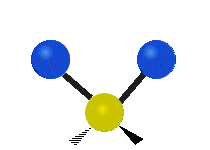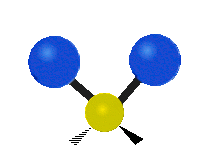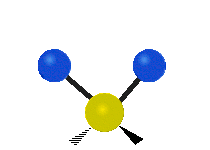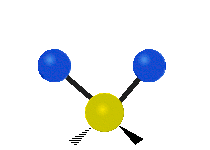
The normal modes of vibration are: asymmetric, symmetric, wagging, twisting, scissoring, and rocking for polyatomic molecules.
| Symmetric Stretching | Asymmetric Stretching | Wagging |
|---|---|---|
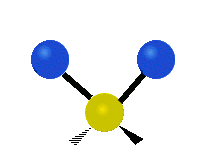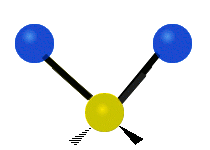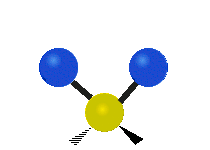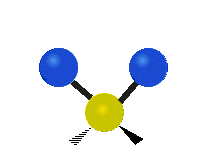 |
 |
 |
| Twisting | Scissoring | Rocking |
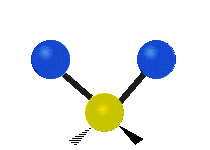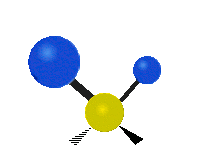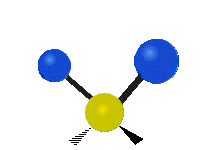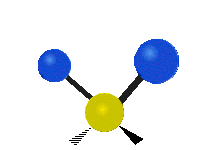 |
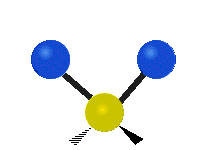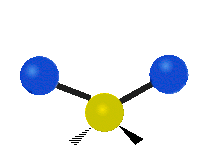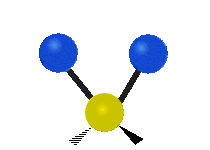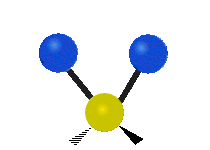 |
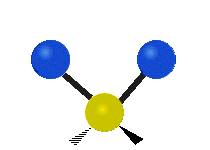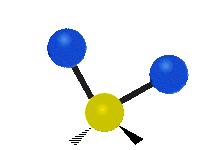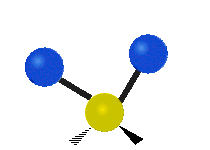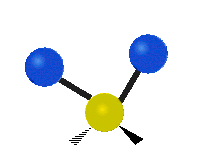 |
Figure \(\PageIndex{1}\): Six types of Vibrational Modes. Images used with permission (Public Domain; Tiago Becerra Paolini).
Calculate Number of Vibrational Modes
Degree of freedom is the number of variables required to describe the motion of a particle completely. For an atom moving in 3-dimensional space, three coordinates are adequate so its degree of freedom is three. Its motion is purely translational. If we have a molecule made of N atoms (or ions), the degree of freedom becomes 3N, because each atom has 3 degrees of freedom. Furthermore, since these atoms are bonded together, all motions are not translational; some become rotational, some others vibration. For non-linear molecules, all rotational motions can be described in terms of rotations around 3 axes, the rotational degree of freedom is 3 and the remaining 3N-6 degrees of freedom constitute vibrational motion. For a linear molecule however, rotation around its own axis is no rotation because it leave the molecule unchanged. So there are only 2 rotational degrees of freedom for any linear molecule leaving 3N-5 degrees of freedom for vibration.
The degrees of vibrational modes for linear molecules can be calculated using the formula:
\[3N-5 \label{1}\]
The degrees of freedom for nonlinear molecules can be calculated using the formula:
\[3N-6 \label{2}\]
\(n\) is equal to the number of atoms within the molecule of interest. The following procedure should be followed when trying to calculate the number of vibrational modes:
- Determine if the molecule is linear or nonlinear (i.e. Draw out molecule using VSEPR). If linear, use Equation \ref{1}. If nonlinear, use Equation \ref{2}
- Calculate how many atoms are in your molecule. This is your \(N\) value.
- Plug in your \(N\) value and solve.
How many vibrational modes are there in the linear \(\ce{CO_2}\) molecule ?
- Answer
-
There are a total of \(3\) atoms in this molecule. It is a linear molecule so we use Equation \ref{1}. There are \[3(3)-5 = 4 \nonumber\] vibrational modes in \(\ce{CO_2}\).
Would \(\ce{CO_2}\) and \(\ce{SO_2}\) have a different number for degrees of vibrational freedom? Following the procedure above, it is clear that \(\ce{CO_2}\) is a linear molecule while \(\ce{SO_2}\) is nonlinear. \(\ce{SO_2}\) contains a lone pair which causes the molecule to be bent in shape, whereas, \(\ce{CO_2}\) has no lone pairs. It is key to have an understanding of how the molecule is shaped. Therefore, \(\ce{CO_2}\) has 4 vibrational modes and \(\ce{SO_2}\) has 3 modes of freedom.
- Followup (\(\ce{SO_2}\))
-
Would \(\ce{CO_2}\) and \(\ce{SO_2}\) have a different number for degrees of vibrational freedom? Following the procedure above, it is clear that \(\ce{CO_2}\) is a linear molecule while \(\ce{SO_2}\) is nonlinear. \(\ce{SO_2}\) contains a lone pair which causes the molecule to be bent in shape, whereas, \(\ce{CO_2}\) has no lone pairs. It is key to have an understanding of how the molecule is shaped. Therefore, \(\ce{CO_2}\) has 4 vibrational modes and \(\ce{SO_2}\) has 3 modes of freedom.
How many vibrational modes are there in the tetrahedral \(\ce{CH_4}\) molecule ?
- Answer
-
In this molecule, there are a total of 5 atoms. It is a nonlinear molecule so we use Equation \ref{2}. There are \[3(5)-6 = 9\nonumber\] vibrational modes in \(\ce{CH_4}\).
How many vibrational modes are there in the nonlinear \(\ce{C_{60}}\) molecule ?
- Answer
-
In this molecule, there are a total of 60 carbon atoms. It is a nonlinear molecule so we use Equation \ref{2}. There are \[3(60)-6 = 174\nonumber\] vibrational modes in \(\ce{C_60}\).
References
- Harris, Daniel C., and Michael D. Bertolucci. Symmetry and Spectroscopy: an Introduction to Vibrational and Electronic Spectroscopy. New York: Dover Publications, 1989. Print.
- Housecroft, Catherine E., and Alan G. Sharpe. Inorganic Chemistry. Harlow: Pearson Education, 2008. Print.

