Selection rules and transition moment integral
- Page ID
- 1784
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In chemistry and physics, selection rules define the transition probability from one eigenstate to another eigenstate. In this topic, we are going to discuss the transition moment, which is the key to understanding the intrinsic transition probabilities. Selection rules have been divided into the electronic selection rules, vibrational selection rules (including Franck-Condon principle and vibronic coupling), and rotational selection rules.
Introduction
The transition probability is defined as the probability of particular spectroscopic transition to take place. When an atom or molecule absorbs a photon, the probability of an atom or molecule to transit from one energy level to another depends on two things: the nature of initial and final state wavefunctions and how strongly photons interact with an eigenstate. Transition strengths are used to describe transition probability. Selection rules are utilized to determine whether a transition is allowed or not. Electronic dipole transitions are by far the most important for the topics covered in this module.
Transition Moment
In an atom or molecule, an electromagnetic wave (for example, visible light) can induce an oscillating electric or magnetic moment. If the frequency of the induced electric or magnetic moment is the same as the energy difference between one eigenstate Ψ1 and another eigenstate Ψ2, the interaction between an atom or molecule and the electromagnetic field is resonant (which means these two have the same frequency). Typically, the amplitude of this (electric or magnetic) moment is called the transition moment. In quantum mechanics, the transition probability of one molecule from one eigenstate Ψ1 to another eigenstate Ψ2 is given by |\(\vec{M}_{21}\)|2, and \(\vec{M}_{21}\) is called the transition dipole moment, or transition moment, from Ψ1 to Ψ2. In mathematical form it can be written as
\[\vec{M}_{21}=\int \Psi_2\vec{\mu}\Psi_1d\tau\]
The Ψ1 and Ψ2 are two different eigenstates in one molecule, \(\vec{M}_{21}\) is the electric dipole moment operator. If we have a system with n molecules and each has charge Qn, and the dipole moment operator is can be written as
\[ \vec{\mu}=\sum_{n}Q_n\vec{x}_n\]
the \(\vec{x}_{n}\) is the position vector operator.
Transition Moment Integral
Based on the Born-Oppenheimer approximation, the fast electronic motion can be separated from the much slower motion of the nuclei. As a result, the total wavefunction can be separated into electronic, vibrational, and rotational parts:
\(\Psi (r,R) = \psi _e (r,R_e )\psi _v (R)\psi _r (R)\)
The Born-Oppenheimer approximation assumes that the electronic wavefunction, \(\psi _e\), is approximated in all electronic coordinates at the equilibrium nuclear coordinates (Re). Since mass of electrons is much smaller than nuclear mass, the rotational wavefunction, \(\psi _r\), only depends on nuclear coordinates. The rotational wavefunction could provide important information for rotational selection rules, but we will not consider the rotational wavefuntion any further for simplicity because most of the spectra are not rotationally resolved. With the rotational part removed, the transition moment integral can be expressed as
\(\ M = \iint {\psi _e '(r,R_e )}\cdot \psi _v '(R)(\mu _e + \mu _n )\psi _e ''(r,R_e ) \cdot \psi _v ''(R)drdR\)
where the prime and double prime represent the upper and lower states respectively. Both the nuclear and electronic parts contribute to the dipole moment operator. The above equation can be integrated by two parts, with \(\mu _n\) and \(\mu _e\) respectively. A product of two integral is obtained:
\(\ M = \int {\psi _e '(r,R_e )} \cdot \mu _e \cdot \psi _e ''(r,R_e )dr\int {\psi _v '(R)} \cdot \psi _v ''(R)dR + \int {\psi _v '(R)} \cdot \mu _n \cdot \psi _v ''(R)dR\int {\psi _e '(r,R_e )} \psi _e ''(r,R_e )dr\)
Because different electronic wavefunctions must be orthogonal to each other, hence \(\int {\psi _e '(r,R_e )} \psi _e ''(r,R_e )dr\) is zero, the second part of the integral should be zero.
The transition moment integral can be simplified as
\(\ M = \int {\psi _e '(r,R_e )} \cdot \mu _e \cdot \psi _e ''(r,R_e )dr\int {\psi _v '(R)} \cdot \psi _v ''(R)dR\)
The above equation is of great importance because the first integral defines the electronic selection rules, while the second integral is the basis of vibrational selection rules.
Electronic Selection Rules
In atoms
Atoms are described by the primary quantum number n, angular momentum quantum number L, spin quantum number S, and total angular momentum quantum number J. Based on Russell-Saunders approximation of electron coupling, the atomic term symbol can be represented as 2S+1LJ.
- The total spin cannot change, ΔS=0;
- The change in total orbital angular momentum can be ΔL=0, \(\pm\)1, but L=0 \(\leftrightarrow\) L=0 transition is not allowed;
- The change in the total angular momentum can be ΔJ=0, \(\pm\)1, but J=0 \(\leftrightarrow\) J=0 transition is not allowed;
- The initial and final wavefunctions must change in parity. Parity is related to the orbital angular momentum summation over all elections Σli, which can be even or odd; only even \(\leftrightarrow\) odd transitions are allowed.
In molecules
The electronic-state configurations for molecules can be described by the primary quantum number n, the angular momentum quantum number Λ, the spin quantum number S, which remains a good quantum number, the quantum number Σ (S, S-1, ..., -S), and the projection of the total angular momentum quantum number onto the molecular symmetry axis Ω, which can be derived as Ω=Λ+Σ. The term symbol for the electronic states can be represented as
\[^{2S+1} \Lambda_{\Omega,(g/u)}^{(+/-)}\]
Group theory makes great contributions to the prediction of the electronic selection rules for many molecules. An example is used to illustrate the possibility of electronic transitions via group theory.
1. The total spin cannot change, ΔS=0; the rule ΔΣ=0 holds for multiplets;
If the spin-orbit coupling is not large, the electronic spin wavefunction can be separated from the electronic wavefunctions. Since the electron spin is a magnetic effect, electronic dipole transitions will not alter the electron spin. As a result, the spin multiplicity should not change during the electronic dipole transition.
2. The total orbital angular momentum change should be ΔΛ=0, \(\pm\)1;
For heteronuclear diatomic molecules with \(\ C_{\infty v} \) symmetry, a Σ+ \(\leftrightarrow\) \(\Pi\) transition is allowed according to ΔΛ selection rule. In order to prove the allowance of this transition, the direct product of \(\Sigma ^ + \otimes \Pi\) yields \(\Pi\) irreducible representation from the direct product table. Based on the \(\ C_{\infty v} \) character table below, the operator in the x and y direction have doubly degenerate \(\Pi\) symmetry. Therefore, the transition between Σ+ \(\leftrightarrow\) \(\Pi\) must be allowed since the multiplication of any irreducible representation with itself will provide the totally symmetric representation. The electronic transition moment integral can be nonzero. We can use the same kind of argument to illustrate that \(\Sigma ^ - \leftrightarrow \Phi\) transition is forbidden.
\(C_{\infty v}\) character table
| \( C_{\infty v}\) | E | \(2C_{\infty ^\Phi}\) | ... | \(\infty \sigma_v\) | ||
|---|---|---|---|---|---|---|
| Σ+ | 1 | 1 | ... | 1 | z | (x2+y2), z2 |
| Σ- | 1 | 1 | ... | -1 | Rz | |
| \(\Pi\) | 2 | \(2\cos (\Phi )\) | ... | 0 | (x, y), (Rx, Ry) | xz, yz |
| \(\Delta\) | 2 | \(2\cos (2 \Phi )\) | ... | 0 | (x2-y2), xy | |
| \(\Gamma\) | 2 | \(2\cos (3 \Phi )\) | ... | 0 | ||
| ... | ... | ... | ... | ... |
3. Parity conditions are related to the symmetry of the molecular wavefunction reflecting against its symmetry axis. For homonuclear molecules, the g \(\leftrightarrow\) u transition is allowed. For heteronuclear molecules, + \(\leftrightarrow\) + and - \(\leftrightarrow\) - transitions apply;
- For hetero diatomic molecules with \(\ C_{\infty v} \) symmetry, we can use group theory to reveal that \(\Sigma ^ + \leftrightarrow \Sigma ^ +\) and \(\Sigma ^ - \leftrightarrow \Sigma ^ -\) transitions are allowed, while \(\Sigma ^ + \leftrightarrow \Sigma ^ -\) transitions are forbidden. The direct product of either \(\Sigma ^ + \otimes \Sigma ^ +\) or \(\Sigma ^ - \otimes \Sigma ^ -\) yields the same irreducible representation Σ+ based on the direct product table. The z component of the dipole operator has Σ+ symmetry. The transition is allowed because the electronic transition moment integral can generate the totally symmetric irreducible representation Σ+. We can use the same method to prove that \(\Sigma ^ + \leftrightarrow \Sigma ^ -\) transitions are forbidden.
- Similarly, for a molecule with an inversion center, a subscript g or u is used to reveal the molecular symmetry with respect to the inversion operation, i. The x, y, and z components of the transition dipole moment operator have u inversion symmetry in molecule with inversion center (g and u are short for gerade and ungerade in German, meaning even and odd). The electronic transition moment integral need to yield totally symmetric irreducible representation Ag for allowed transitions. Therefore, only g \(\leftrightarrow\) u transition is allowed.
Vibrational Selection rules
- Transitions with Δv=\(\pm\)1, \(\pm\)2, ... are all allowed for anharmonic potential, but the intensity of the peaks become weaker as Δv increases.
- v=0 to v=1 transition is normally called the fundamental vibration, while those with larger Δv are called overtones.
- Δv=0 transition is allowed between the lower and upper electronic states with energy E1 and E2 are involved, i.e. (E1, v''=n) \(\to\) (E2, v'=n), where the double prime and prime indicate the lower and upper quantum state.
The geometry of vibrational wavefunctions plays an important role in vibrational selection rules. For diatomic molecules, the vibrational wavefunction is symmetric with respect to all the electronic states. Therefore, the Franck-Condon integral is always totally symmetric for diatomic molecules. The vibrational selection rule does not exist for diatomic molecules.
For polyatomic molecules, the nonlinear molecules possess 3N-6 normal vibrational modes, while linear molecules possess 3N-5 vibrational modes. Based on the harmonic oscillator model, the product of 3N-6 normal mode wavefunctions contribute to the total vibrational wavefunction, i.e.
\[\psi _{vib} = \prod\limits_{3N - 6} {\psi _1 \psi _2 } \psi _3 ...\psi _{3N - 6}\]
where each normal mode is represented by the wavefunction \(\psi_i\). Comparing to the Franck-Condon factor for diatomic molecules with single vibrational overlap integral, a product of 3N-6 (3N-5 for linear molecules) overlap integrals needs to be evaluated. Based on the symmetry of each normal vibrational mode, polyatomic vibrational wavefunctions can be totally symmetric or non-totally symmetric. If a normal mode is totally symmetric, the vibrational wavefunction is totally symmetric with respect to all the vibrational quantum number v. If a normal mode is non-totally symmetric, the vibrational wavefunction alternates between symmetric and non-symmetric wavefunctions as v alternates between even and odd number.
If a particular normal mode in both the upper and lower electronic state is totally symmetric, the vibrational wavefunction for the upper and lower electronic state will be symmetric, resulting in the totally symmetric integrand in the Franck-Condon integral. If the vibrational wavefunction of either the lower or upper electronic state is non-totally symmetric, the Franck-Condon integrand will be non-totally symmetric.
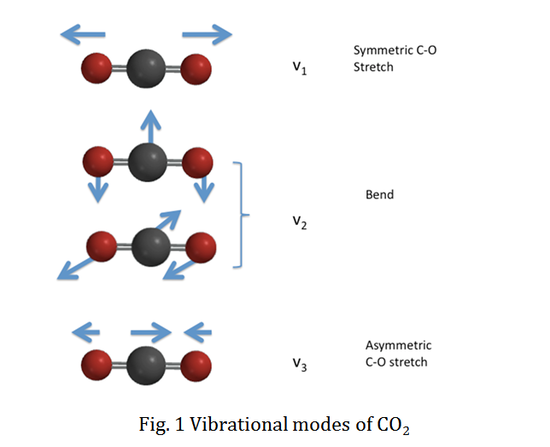
We will use CO2 as an example to specify the vibrational selection rule. CO2 has four vibrational modes as a linear molecule. The vibrational normal modes are illustrated in the figure below:
The vibrational wavefunction for the totally symmetric C-O stretch, v1, is totally symmetric with respect to all the vibrational quantum numbers. However, the vibrational wavefunctions for the doubly degenerate bending modes, v2, and the antisymmetric C-O stretch, v3, are non-totally symmetric. Therefore, the vibrational wavefunctions are totally symmetric for even vibrational quantum numbers (v=0, 2, 4...), while the wavefunctions remain non-totally symmetric for v odd (v=1, 3, 5...).
Therefore, any value of Δv1 is possible between the upper and lower electronic state for mode v1. On the other hand, modes v2 and v3 include non-totally symmetric vibrational wavefunctions, so the vibrational quantum number can only change evenly, such as Δv=\(\pm\) 2, \(\pm\) 4, etc..
Franck-Condon Principle
Franck-Condon principle was proposed by German physicist James Franck (1882-1964) and U.S. physicist Edward U. Condon (1902-1974) in 1926. This principle states that when an electronic transition takes place, the time scale of this transition is so fast compared to nucleus motion that we can consider the nucleus to be static, and the vibrational transition from one vibrational state to another state is more likely to happen if these states have a large overlap. It successfully explains the reason why certain peaks in a spectrum are strong while others are weak (or even not observed) in absorption spectroscopy.
\(\ M = \int {\psi _e '(r,R_e )} \cdot \mu _e \cdot \psi _e ''(r,R_e )dr\int {\psi _v '(R)} \cdot \psi _v ''(R)dR\)
The second integral in the above equation is the vibrational overlap integral between one eigenstate and another eigenstate. In addition, the square of this integral is called the Franck-Condon factor:
\(\displaystyle \ Franck-Condon \; Factor = \mid \int {\psi _v '}\psi _v ''dR\mid^2\)
It governs the vibrational transition contribution to the transition probability and shows that in order to have a large vibrational contribution, the vibrational ground state and excited state must have a strong overlap.
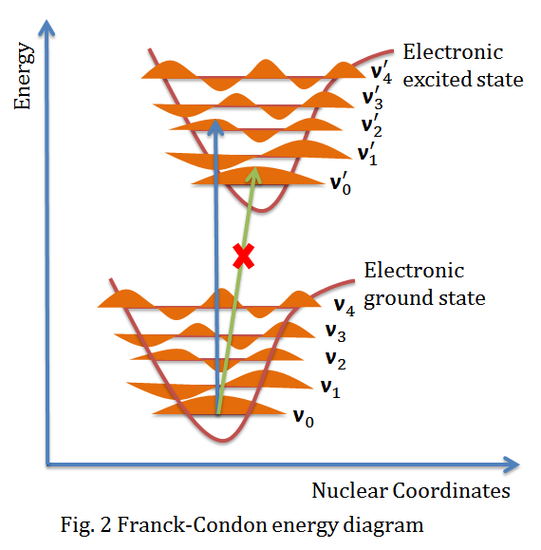
The above figure shows the Franck-Condon principle energy diagram, since electronic transition time scale is small compared to nuclear motion, the vibrational transitions are favored when the vibrational transition have the smallest change of nuclear coordinate, which is a vertical transition in the figure above. The electronic eigenstates favors the vibrational transition v'=0 in the ground electronic state to v"=2 in the excited electronic state, while peak intensity of v'=0 to v"=0 transition is expected to be low because the overlap between the v'=0 wavefunction and v''=0 wavefunction is very low.
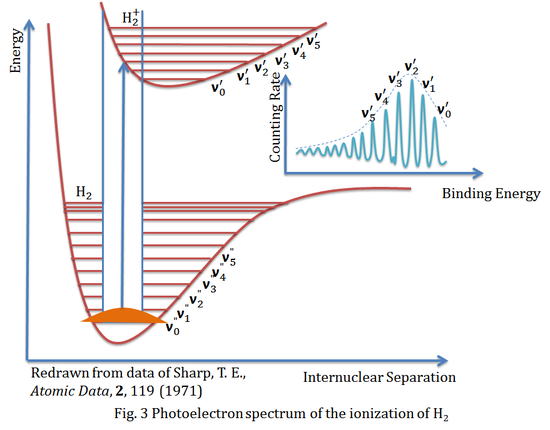
The figure above is the photoelectron spectrum of the ionization of hydrogen molecule (H2), it is also a beautiful example to formulate the Franck-Condon principle. It shows the appropriate energy curves and the vibrational energy levels, and with the help of the Franck-Condon principle, the transition between ground vibrational state v0" and excited vibrational state v2' is expected to be the most intense peak in the spectrum.
Vibronic Coupling
Why can some electronic-forbidden transitions be observed as weak bands in spectrum? It can be explained by the interaction between the electronic and vibrational transitions. The word "vibronic" is the combination of the words "vibrational" and "electronic." Because the energy required for one electronic state to another electronic state (electronic transition, usually in the UV-Vis region) is larger than one vibrational state to another vibrational state (vibrational transition, usually in the IR region), sometimes energy (a photon) can excite a molecule to an excited electronic and vibrational state. The bottom figure shows the pure electronic transition (no vibronic coupling) and the electronic transition couples with the vibrational transition (vibronic coupling).

We now can go back to the original question: Why can some electronic-forbidden transitions be observed as weak bands in spectrum? For example, the d-d transitions in the octahedral transition metal complexes are Laporte forbidden (same symmetry, parity forbidden), but they can be observed in the spectrum and this phenomenon can be explained by vibronic coupling.

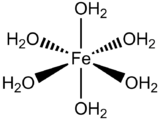
Now we consider the Fe(OH2)62+ complex which has low spin d6 as ground state (see figure above). Let's examine the one-electron excitation from t2g molecular orbital to eg molecular orbital. The octahedral complex has Oh symmetry and therefore the ground state has A1g symmetry from the character table. The symmetry of the excited state, which is the direct product of all singly occupied molecular orbitals (eg and t2g in this case):
\(\displaystyle \Gamma_{t_{2g}}\otimes\Gamma_{e_g}= T_{1g}+T_{2g}\)
The transition moment integral for the electronic transition can be written as
\(\vec{M}=\int \psi^{'*}\vec{\mu}\psi d\tau\)
where ψ is the electronic ground state and ψ' is the electronic excited state. The condition for the electronic transition to be allowed is to make the transition moment integral nonzero. The \(\hat{\mu}\) is the transition moment operator, which is the symmetry of the \(\hat{x}\), \(\hat{y}\), \(\hat{z}\) operators from the character table. For octahedral symmetry, these operators are degenerate and have T1u symmetry. Therefore, we can see that both 1T1g←1A1g and 1T2g←1A1g are electronically forbidden by the direct product (do not contain the totally symmetric A1g):
\(\displaystyle T_{1g}\times\ T_{1u}\times\ A_{1g}= A_{1u}+E_{u}+T_{1u}+T_{2u}\)
\(\displaystyle T_{2g}\times\ T_{1u}\times\ A_{1g}= A_{2u}+E_{u}+T_{1u}+T_{2u}\)
For octahedral complex, there are 15 vibrational normal modes. From the Oh character table we can get these irreducible representations:
\(\displaystyle \Gamma_{vib}= a_{1g}+e_{g}+2t_{1u}+t_{2g}+t_{2u}\)
When we let the vibrational transition to couple with the electronic transition, the transition moment integral has the form:
\(\displaystyle \vec{M}=\int \psi_{e'}^{*} \psi_{v'}^{*} \vec{\mu} \psi_e \psi_v d\tau\)
For the vibronic coupling to be allowed, the transition moment integral has to be nonzero. Use these vibrational symmetries of the octahedral complex to couple with the electronic transition:
\(\displaystyle A_{1g}\times \{T_{1g}\times\ T_{1u}\times\ A_{1g}\}= A_{1u}+E_{u}+T_{1u}+T_{2u}\)
\(\displaystyle E_{g}\times \{T_{1g}\times\ T_{1u}\times\ A_{1g}\}= E_{g}\times \{A_{1u}+E_{u}+T_{1u}+T_{2u}\}=A_{1u}+A_{2u}+2E_{u}+2T_{1u}+2T_{2u}\)
\(\displaystyle T_{1u}\times \{T_{1g}\times\ T_{1u}\times\ A_{1g}\}= T_{1u}\times \{A_{1u}+E_{u}+T_{1u}+T_{2u}\}=A_{1g}+ \ldots\)
\(\displaystyle T_{2g}\times \{T_{1g}\times\ T_{1u}\times\ A_{1g}\}= T_{2g}\times \{A_{1u}+E_{u}+T_{1u}+T_{2u}\}=A_{1u}+A_{2u}+2E_{u}+3T_{1u}+4T_{2u}\)
\(\displaystyle T_{2u}\times \{T_{1g}\times\ T_{1u}\times\ A_{1g}\}= T_{2u}\times \{A_{1u}+E_{u}+T_{1u}+T_{2u}\}=A_{1g}+ \ldots\)
Since the t1u and t2u representation can generate the totally symmetric representation in the integrand. Therefore, we can see that t1u and t2u can couple with the electronic transition to form the allowed vibronic transition. Therefore, the d-d transition band for Fe(OH2)62+ complex can be observed through vibronic coupling.
Rotational Selection rules
1. Transitions with ΔJ=\(\pm\)1 are allowed;
Photons do not have any mass, but they have angular momentum. The conservation of angular momentum is the fundamental criteria for spectroscopic transitions. As a result, the total angular momentum has to be conserved after a molecule absorbs or emits a photon. The rotational selection rule relies on the fact that photon has one unit of quantized angular momentum. During the photon emission and absorption process, the angular moment J cannot change by more than one unit.
Let's consider a single photon transition process for a diatomic molecule. The rotational selection rule requires that transitions with ΔJ=\(\pm\)1 are allowed. Transitions with ΔJ=1 are defined as R branch transitions, while those with ΔJ=-1 are defined as P branch transitions. Rotational transitions are conventional labeled as P or R with the rotational quantum number J of the lower electronic state in the parentheses. For example, R(2) specifies the rotational transition from J=2 in the lower electronic state to J=3 in the upper electronic state.
2. ΔJ=0 transitions are allowed when two different electronic or vibrational states are involved: (X'', J''=m) \(\to\) (X', J'=m).
The Q branch transitions will only take place when there is a net orbital angular momentum in one of the electronic states. Therefore, Q branch does not exist for \(\ {}^1\Sigma \leftrightarrow {}^1\Sigma\) electronic transitions because \(\Sigma\) electronic state does not possess any net orbital angular momentum. On the other hand, the Q branch will exist if one of the electronic states has angular momentum. In this situation, the angular momentum of the photon will cancel out with the angular momentum of the electronic state, so the transition will take place without any change in the rotational state.
The schematic of P, Q, and R branch transitions are shown below:
With regard to closed-shell non-linear polyatomic molecules, the selection rules are more complicated than diatomic case. The rotational quantum number J remains a good quantum number as the total angular momentum if we don't consider the nuclear spin. Under the effect of single photon transition, the change of J is still limited to a maximum of \(\pm\) 1 based on the conservation of angular momentum. However, the possibility of Q branch is greatly enhanced irrelevant to the symmetry of the lower and upper electronic states. The rotational quantum number K is introduced along the inertial axis. For polyatomic molecules with symmetric top geometry, the transition moment is polarized along inertial axis. The selection rule becomes ΔK=0.
References
- Schwartz, S. E. J. Chem. Educ. 1973, 50, 608-610. doi:10.1021/ed050p608
- Byers, L. R. J. Chem. Educ. 1975, 52, 790. doi:10.1021/ed052p790
- Ahmed, F. J. Chem. Educ. 1987, 64, 427-428. doi:10.1021/ed064p427
- Dunbrack, R. L. J. Chem. Educ. 1986, 63, 953-955. doi:10.1021/ed063p953
- Standard, J. M., Clark, B. K. J. Chem. Educ. 1999, 76, 1363-1366. doi:10.1021/ed076p1363
- Ellis, A. M., Fehér, M., & Wright, T. G. (2005). Transition probabilities. Electronic and photoelectron spectroscopy: fundamentals and case studies(pp. 51-64). Cambridge: Cambridge University Press.
Problems
- What are the differences between Born-Oppenheimer approximation and Franck-Condon principle?
- In evaluating the transition moment integral, why there must be a totally symmetric irreducible representation to make the transition allowed?
- Because of the d-d transition, transition metal complexes are known for its various color. However, Mn2+ does not have intense color (pale pink), why?
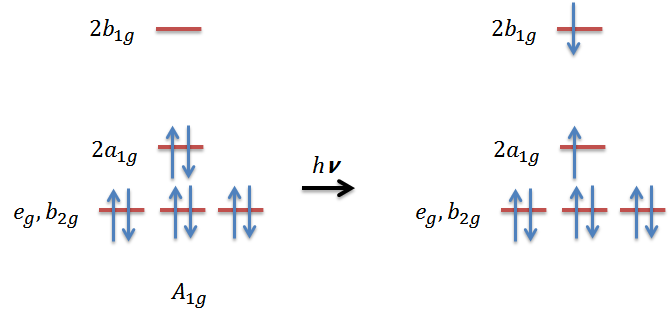
- Assume a Pd2+ square planar complex (D4h symmetry), is the following electronic transition allowed? If not, can it gain intensity by vibronic coupling?
- What's the vibrational selection rule for polyatomic molecules?
- Under what condition can we see the Q branch transition?
Answers to Problems
- The Born Oppenheimer approximation states that the fast electronic motion can be separated from the much slower motion of the nuclei, so the total wavefunction can be separated into the electronic, vibrational and rotational part. The Franck-Condon principle states during an electronic transition, the timescale for an electron to move from one orbital to another is so short that the nuclear position does not change during the transition process. The Franck Condon factor is the square of the overlap integral, which defines the vibrational contribution to the transition probability.
- n the character table, only A1 or A1g are totally symmetric irreducible representations. When you are integrating an odd function over space, the integrand will be 0. Only the integration of an even function over space will yield a non-zero value, representing the possibility of the transition.
- The ground state Mn2+ has a high spin d5 electronic configuration, which has one electron in each of the eg and t2g orbitals, and according to the electronic transition selection rule, the total spin cannot change:
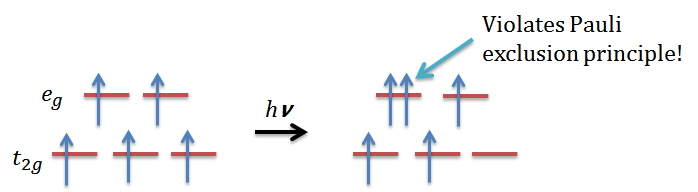
then we will find out it is impossible for a high spin d5 octahedral complex since it violates Pauli exclusion principle. Therefore, the d-d transition for this is Laporte forbidden and also spin forbidden, resulting in a pale color.
4. The symmetry of the excited state will have the symmetry:
\[\Gamma_{a_{1g}}\otimes\Gamma_{b_{1g}}= B_{1g}\]
In the point group of D4h, the dipole moment operator transforms as eu(x,y) and a2u(z). Then by evaluating the transition moment integral for the electronic transition, we can easily find out that there is no totally symmetric irreducible representation in the integrand.Therefore, the electronic transition is not allowed:
\[B_{1g}\times\dbinom{E_u}{A_{2u}}\times\ A_{1g}= \dbinom{E_u}{B_{2u}}\]
Next step we examine the vibrational irreducible representation a D4h complex has:
\[ \Gamma_{vib}= a_{1g}+b_{1g}+b_{2g}+a_{2u}+b_{2u}+2e_{u}\]
we can see that eu and b2u can potentially serve as the promoting mode for vibronic transition, that is, generating the totally symmetric A1g in the integrand. Therefore, this electronic transition for D4h complex is forbidden, however, the transition can be allowed through vibronic coupling.
5. If the vibrational mode is totally symmetric, any change in the vibrational quantum number v is possible between the lower electronic state and upper electronic state. If the vibrational mode is non-totally symmetric, the vibrational wavefunction for the lower and upper electronic states are non-totally symmetric. The vibrational quantum number can only change evenly, such as Δv=\(\pm\) 2, \(\pm\) 4, etc..
6.The Q branch transitions will only take place when there is a net orbital angular momentum in one of the electronic states.