Hybrid Orbitals

Hybridization was introduced to explain molecular structure when the valence bond theory failed to correctly predict them. It is experimentally observed that bond angles in organic compounds are close to 109^o, 120^o, or 180^o. According to Valence Shell Electron Pair Repulsion (VSEPR) theory, electron pairs repel each other and the bonds and lone pairs around a central atom are generally separated by the largest possible angles.

Introduction

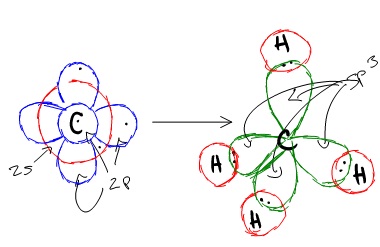
Carbon is a perfect example showing the value of hybrid orbitals. Carbon's ground state configuration is:

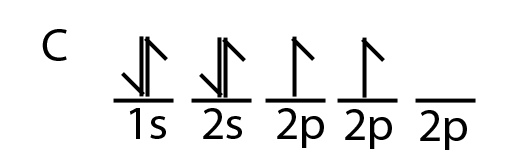
According to Valence Bond Theory, carbon should form two covalent bonds, resulting in a CH₂, because it has two unpaired electrons in its electronic configuration.However, experiments have shown that \(CH_2\) is highly reactive and cannot exist outside of a reaction. Therefore, this does not explain how CH₄ can exist. To form four bonds the configuration of carbon must have four unpaired electrons.

One way CH₄ can be explained is, the 2s and the 3 2p orbitals combine to make four, equal energy sp³ hybrid orbitals. That would give us the following configuration:

Now that carbon has four unpaired electrons it can have four equal energy bonds. The hybridization of orbitals is favored because hybridized orbitals are more directional which leads to greater overlap when forming bonds, therefore the bonds formed are stronger. This results in more stable compounds when hybridization occurs.

The next section will explain the various types of hybridization and how each type helps explain the structure of certain molecules.

sp³ hybridization

sp³ hybridization can explain the tetrahedral structure of molecules. In it, the 2s orbitals and all three of the 2p orbitals hybridize to form four sp³ orbitals, each consisting of 75% p character and 25% s character. The frontal lobes align themselves in the manner shown below. In this structure, electron repulsion is minimized.

Energy changes occurring in hybridization

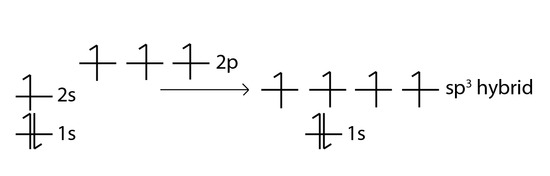
Hybridization of an s orbital with all three p orbitals (p_x , p_y, and p_z) results in four sp³ hybrid orbitals. sp³ hybrid orbitals are oriented at bond angle of 109.5^o from each other. This 109.5^o arrangement gives tetrahedral geometry (Figure 4).

Example: sp^3 Hybridization in Methane

Because carbon plays such a significant role in organic chemistry, we will be using it as an example here. Carbon's 2s and all three of its 2p orbitals hybridize to form four sp^3 orbitals. These orbitals then bond with four hydrogen atoms through sp^3-s orbital overlap, creating methane. The resulting shape is tetrahedral, since that minimizes electron repulsion. Hybridization Lone Pairs: Remember to take into account lone pairs of electrons. These lone pairs cannot double bond so they are placed in their own hybrid orbital. This is why H2O is tetrahedral. We can also build sp3d and sp3d2 hybrid orbitals if we go beyond s and p subshells.

sp² hybridization

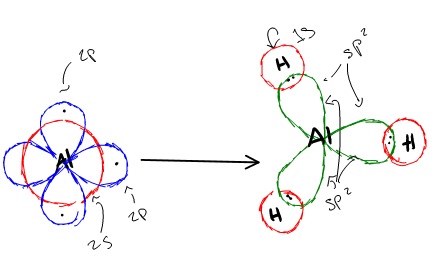
sp² hybridization can explain the trigonal planar structure of molecules. In it, the 2s orbitals and two of the 2p orbitals hybridize to form three sp orbitals, each consisting of 67% p and 33% s character. The frontal lobes align themselves in the trigonal planar structure, pointing to the corners of a triangle in order to minimize electron repulsion and to improve overlap. The remaining p orbital remains unchanged and is perpendicular to the plane of the three sp² orbitals.

Energy changes occurring in hybridization

Hybridization of an s orbital with two p orbitals (p_x and p_y) results in three sp² hybrid orbitals that are oriented at 120^o angle to each other (Figure 3). Sp² hybridization results in trigonal geometry.

Example: sp^2 Hybridization in Aluminum Trihydride
In aluminum trihydride, one 2s orbital and two 2p orbitals hybridize to form three sp^2 orbitals that align themselves in the trigonal planar structure. The three Al sp^2 orbitals bond with with 1s orbitals from the three hydrogens through sp^2-s orbital overlap.

Example: sp^2 Hybridization in Ethene

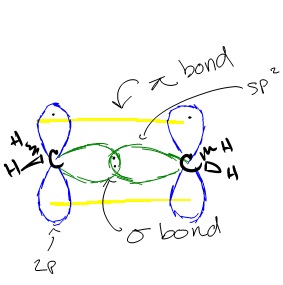
Similar hybridization occurs in each carbon of ethene. For each carbon, one 2s orbital and two 2p orbitals hybridize to form three sp^2 orbitals. These hybridized orbitals align themselves in the trigonal planar structure. For each carbon, two of these sp orbitals bond with two 1s hydrogen orbitals through s-sp orbital overlap. The remaining sp^2 orbitals on each carbon are bonded with each other, forming a bond between each carbon through sp^2-sp^2 orbital overlap. This leaves us with the two p orbitals on each carbon that have a single carbon in them. These orbitals form a ? bonds through p-p orbital overlap, creating a double bond between the two carbons. Because a double bond was created, the overall structure of the ethene compound is linear. However, the structure of each molecule in ethene, the two carbons, is still trigonal planar.

sp Hybridization

sp Hybridization can explain the linear structure in molecules. In it, the 2s orbital and one of the 2p orbitals hybridize to form two sp orbitals, each consisting of 50% s and 50% p character. The front lobes face away from each other and form a straight line leaving a 180° angle between the two orbitals. This formation minimizes electron repulsion. Because only one p orbital was used, we are left with two unaltered 2p orbitals that the atom can use. These p orbitals are at right angles to one another and to the line formed by the two sp orbitals.

Energy changes occurring in hybridization

Figure 1: Notice how the energy of the electrons lowers when hybridized.

These p orbitals come into play in compounds such as ethyne where they form two addition? bonds, resulting in in a triple bond. This only happens when two atoms, such as two carbons, both have two p orbitals that each contain an electron. An sp hybrid orbital results when an s orbital is combined with p orbital (Figure 2). We will get two sp hybrid orbitals since we started with two orbitals (s and p). sp hybridization results in a pair of directional sp hybrid orbitals pointed in opposite directions. These hybridized orbitals result in higher electron density in the bonding region for a sigma bond toward the left of the atom and for another sigma bond toward the right. In addition, sp hybridization provides linear geometry with a bond angle of 180^o.

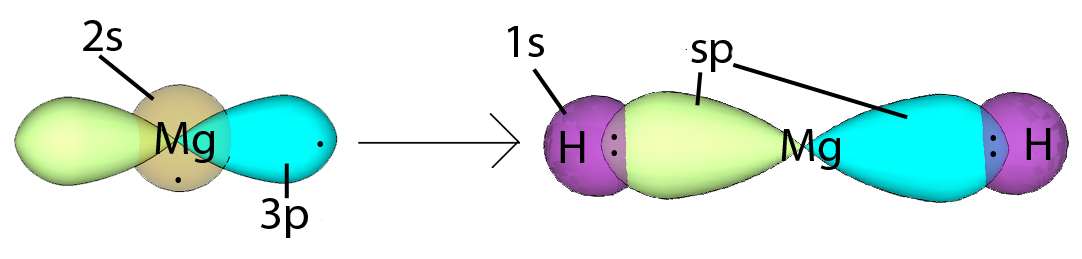
Example: sp Hybridization in Magnesium Hydride
In magnesium hydride, the 3s orbital and one of the 3p orbitals from magnesium hybridize to form two sp orbitals. The two frontal lobes of the sp orbitals face away from each other forming a straight line leading to a linear structure. These two sp orbitals bond with the two 1s orbitals of the two hydrogen atoms through sp-s orbital overlap. Hybridization

Example: sp Hybridization in Ethyne

The hybridization in ethyne is similar to the hybridization in magnesium hydride. For each carbon, the 2s orbital hybridizes with one of the 2p orbitals to form two sp hybridized orbitals. The frontal lobes of these orbitals face away from each other forming a straight line. The first bond consists of sp-sp orbital overlap between the two carbons. Another two bonds consist of s-sp orbital overlap between the sp hybridized orbitals of the carbons and the 1s orbitals of the hydrogens. This leaves us with two p orbitals on each carbon that have a single carbon in them. This allows for the formation of two ? bonds through p-p orbital overlap. The linear shape, or 180° angle, is formed because electron repulsion is minimized the greatest in this position. Hybridization

References

1. John Olmsted, Gregory M. Williams Chemistry: The Molecular Science Jones & Bartlett Publishers 1996. 366-371
2. Francis A. Carey Advanced Organic Chemistry Springer 2001. 4-6
3. L. G. Wade, Jr. Whitman College Organic Chemistry Fifth Edition 2003

Problems

Using the Lewis Structures, try to figure out the hybridization (sp, sp², sp³) of the indicated atom and indicate the atom's shape.

1. The carbon.

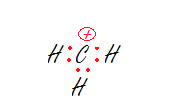
2. The oxygen.

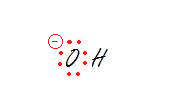
3. The carbon on the right.

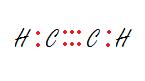
Answers

1. sp²- Trigonal Planar

The carbon has no lone pairs and is bonded to three hydrogens so we just need three hybrid orbitals, aka sp².

2. sp³ - Tetrahedral

Don't forget to take into account all the lone pairs. Every lone pair needs it own hybrid orbital. That makes three hybrid orbitals for lone pairs and the oxygen is bonded to one hydrogen which requires another sp³ orbital. That makes 4 orbitals, aka sp³.

3. sp - Linear

The carbon is bonded to two other atoms, that means it needs two hybrid orbitals, aka sp.

An easy way to figure out what hybridization an atom has is to just count the number of atoms bonded to it and the number of lone pairs. Double and triple bonds still count as being only bonded to one atom. Use this method to go over the above problems again and make sure you understand it. It's a lot easier to figure out the hybridization this way.

Contributors

• Harpreet Chima (UCD), Farah Yasmeen