2.4: Rules for Resonance Forms
- Page ID
- 31387
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)After completing this section, you should be able to
- use the concept of resonance to explain structural features of molecules and ions.
- understand the relationship between resonance and relative stability of molecules and ions.
Rules for Drawing and Working with Resonance Contributors
Recognizing, drawing, and evaluating the relative stability of resonance contributors is essential to understanding organic reaction mechanisms. When learning to draw and interpret resonance structures, there are a few basic guidelines to help. .
- There is ONLY ONE REAL STRUCTURE for each molecule or ion. This real structure (the resonance hybrid) takes its character from the average of all the individual resonance contributors. When looking at a resonance contributors, we are seeing the exact same molecule or ion depicted in different ways. Resonance hybrids are really a single, unchanging structure.
Major resonance contributors of the formate ion
Representations of the formate resonance hybrid
- The resonance hybrid is more stable than any individual resonance structures. Often, resonance structures represent the movement of a charge between two or more atoms. The charge is spread out amongst these atoms and therefore more stabilized. When looking at the picture above the resonance contributors represent the negative charge as being on one oxygen or the other. The resonance hybrid shows the negative charge being shared equally between two oxygens. In the resonance hybrid, the negative charge is spread out over a larger part of the molecule and is therefore more stable.
- Resonance contributors do not have to be equivalent. Because of this, resonance structures do necessarily contribute equally to the resonance hybrid. The two resonance structures shown below are not equivalent because one show the negative charge on an oxygen while the other shows it on a carbon. Later, we will show that the contributor with the negative charge on the oxygen is the more stable of the two. Also, this means that the resonance hybrid will not be an exact mixture of the two structures.
- All resonance contributors must be correct Lewis structures. Each atom should have a complete valence shell and be shown with correct formal charges. A carbocation (carbon with only 6 valence electrons) is the only allowed exception to the valence shell rules. The structure below is an invalid resonance structure even though it only shows the movement of a pi bond. The resulting structure contains a carbon with ten electrons, which violates the octet rule, making it invalid.
- All resonance contributors must have the same molecular formula, the same number of electrons, and same net charge. The molecules in the figure below are not resonance structures of the same molecule because then have different molecular formulas (C2H5NO Vs. C2H6NO). Also, the two structures have different net charges (neutral Vs. positive).
- Resonance contributors only differ by the positions of pi bond and lone pair electrons. Sigma bonds are never broken or made, because of this atoms must maintain their same position. The molecules in the figure below are not resonance structures of the same molecule even though they have the same molecular formula (C3H6O). These molecules are considered structural isomers because their difference involves the breaking of a sigma bond and moving a hydrogen atom.
Major and Minor Resonance Contributors
As previously state the true structure of a resonance hybrid is the combination of all the possible resonance structures. If the resonance structures are equal in stability they the contribute equally to the structure of the hybrid. However, if the resonance structures have different stabilities they contribute to the hybrid's structure in proportions related to their relative stabilities. It can be said the the resonance hybrid's structure resembles the most stable resonance structure. Because of this it is important to be able to compare the stabilities of resonance structures. In the example below, structure B is much less important in terms of its contribution to the hybrid because it contains the violated octet of a carbocation. The relative stabilities of the two structures are so vastly different that molecules which contain a C=O bond are almost exclusively written in a form like structure A. However, as will learn in chapter 19, the positively charged carbon created by structure B will explain how the C=O bond will react with electron rich species.
Rules for Estimating Stability of Resonance Structures
1. The resonance structures in which all atoms have complete valence shells is more stable. This means most atoms have a full octet. In the example below structure A has a carbon atom with a positive charge and therefore an incomplete octet. Based on this criterion, structure A is less stable and is a more minor contributor to the resonance hybrid than structure B.
2. The structures with the least number of formal charges is more stable. Based on this, structure B is less stable because is has two atoms with formal charges while structure A has none. Structure A would be the major resonance contributor.
3. The structures with a negative charge on the more electronegative atom will be more stable. The difference between the two resonance structures is the placement of a negative charge. Structure B is the more stable and the major resonance contributor, because it places the negative charge on the more electronegative oxygen.
4. The structures with a positive charges on the least electronegative atom (most electropositive) is more stable.
5. The structures with the least separation of formal charges is more stable. The only difference between the two structures below are the relative positions of the positive and negative charges. In structure A the charges are closer together making it more stable.
6. Resonance forms that are equivalent have no difference in stability. When looking at the two structures below no difference can be made using the rules listed above. This means the two structures are equivalent in stability and would make equal structural contributions to the resonance hybrid.
Example 1
Example 2
Example 3
Carboxylate example
In the case of carboxylates, contributors A and B below are equivalent in terms of their relative contribution to the hybrid structure. However, there is also a third resonance contributor C, in which the carbon bears a positive formal charge (a carbocation) and both oxygens are single-bonded and bear negative charges.
Structure C makes a less important contribution to the overall bonding picture of the group relative to A and B. How do we know that structure C is the ‘minor’ contributor? Apply the rules below:
- The carbon in contributor C does not have an octet. In general, resonance contributors in which a carbon does not fulfill the octet rule are relatively less important. (rule #1)
- In structure C, there are only three bonds, compared to four in A and B. In general, a resonance structure with a lower number of total bonds is relatively less important. (rule #2)
- Structure C also has more formal charges than are present in A or B. In general, resonance contributors in which there is more/greater separation of charge are relatively less important. (rule #3)
- Structures A and B are equivalent and will be equal contributors to the resonance hybrid. (rule #5).
- The resonance contributor in which a negative formal charge is located on a more electronegative atom, usually oxygen or nitrogen, is more stable than one in which the negative charge is located on a less electronegative atom such as carbon. An example is in the upper left expression in the next figure. (rule #4)
Molecules with Three Resonance Structures
Molecules with more than 2 resonance structures can also be considered using the rules listed above. Of the resonance structures listed below, structure A would be the most stable because all the non-hydrogen atoms have a full octet and the negative charge is on the more electronegative atom (oxygen). Structure C would be next in stability because all of the non-hydrogen atoms have full octets, though now the negative charge is on carbon rather than oxygen. Structure B would be the least stable of the three because it has the carbocation does not have an octet. Of the three, structure A would be the major resonance structure and would most resemble the structure of the true resonance hybrid. Structure B is considered a minor resonance contributor and would have very little effect on the structure of the resonance hybrid.
Draw the major resonance contributor of the structure below. Include in your figure the appropriate curved arrows showing how you got from the given structure to your structure. Explain why your contributor is the major one. In what kind of orbitals are the two lone pairs on the oxygen?
Solution
In the structure above, the carbon with the positive formal charge does not have a complete octet of valence electrons. Using the curved arrow convention, a lone pair on the oxygen can be moved to the adjacent bond to the left, and the electrons in the double bond shifted over to the left (see the rules for drawing resonance contributors to convince yourself that these are 'legal' moves).
The resulting resonance contributor, in which the oxygen bears the formal charge, is the major one because all atoms have a complete octet, and there is one additional bond drawn (resonance rules #1 and #2 both apply). This system can be thought of as four parallel 2p orbitals (one each on C2, C3, and C4, plus one on oxygen) sharing four pi electrons. One lone pair on the oxygen is in an unhybridized 2p orbital and is part of the conjugated pi system, and the other is located in an sp2 orbital.
Also note that one additional contributor can be drawn, but it is also minor because it has a carbon with an incomplete octet:
For the following resonance structures please rank them in order of stability. Indicate which would be the major contributor to the resonance hybrid.
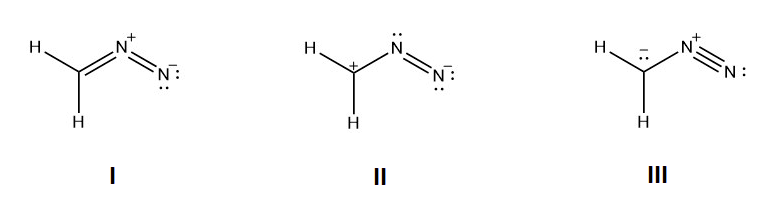
- Answer
-
Structure I would be the most stable because all the non-hydrogen atoms have a full octet and the negative charge is on the more electronegative nitrogen. Structure III would be the next in stability because all of the non-hydrogen atoms have full octets. Structrure II would be the least stable because it has the violated octet of a carbocation.
Draw four additional resonance contributors for the molecule below. Label each one as major or minor (the structure below is of a major contributor).
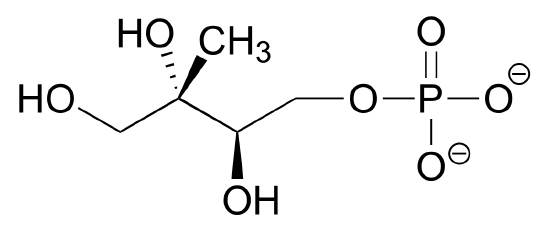
- Answer
-
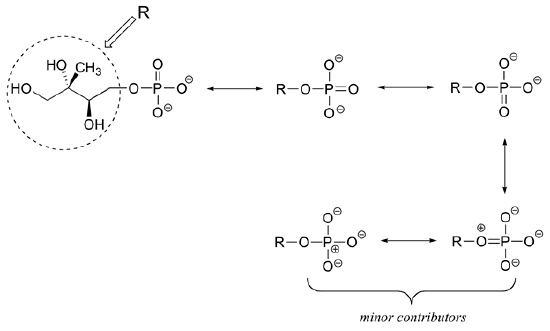
Draw three resonance contributors of methyl acetate (an ester with the structure CH3COOCH3), and order them according to their relative importance to the bonding picture of the molecule. Explain your reasoning.
- Answer
-

- The contributor on the left is the most stable: there are no formal charges.
- The contributor on the right is least stable: there are formal charges, and a carbon has an incomplete octet.
- The contributor in the middle is intermediate stability: there are formal charges, but all atoms have a complete octet.
Below is a minor resonance contributor of a species known as an ‘enamine’, which we will study more in Section 19.8 (formation of enamines) Section 23.12 (reactions of enamines). Draw the major resonance contributor for the enamine, and explain why your contributor is the major one.
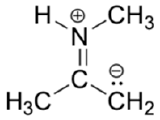
- Answer
-
This contributor is major because there are no formal charges.
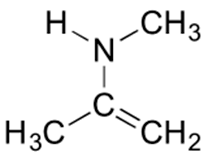
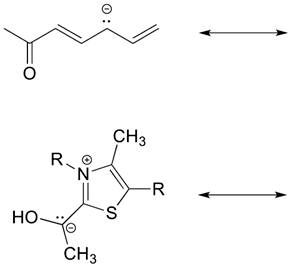
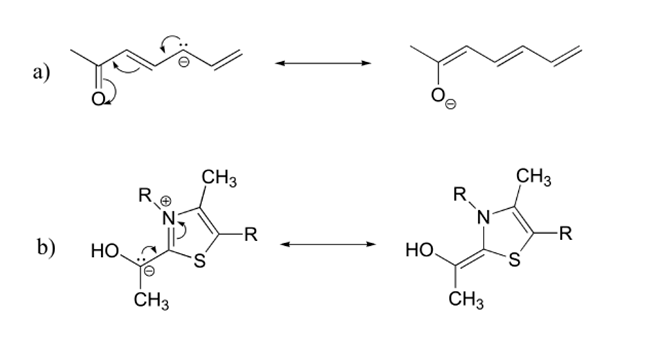
- Answer
-
Are all the bond lengths the same in the carbonate ion, CO32-?
- Answer
-
Yes, the bond lengths in carbonate ion are all the same. Carbonate ion exists as the resonance hybrid of the three resonance forms below.
Additional resonance topics
Recognizing Resonance
Resonance contributors involve the ‘imaginary movement’ of pi-bonded electrons or of lone-pair electrons that are adjacent to (i.e. conjugated to) pi bonds. You can never shift the location of electrons in sigma bonds – if you show a sigma bond forming or breaking, you are showing a chemical reaction taking place. Likewise, the positions of atoms in the molecule cannot change between two resonance contributors.
Because benzene will appear throughout this course, it is important to recognize the stability gained through the resonance delocalization of the six pi electrons throughout the six carbon atoms. Benzene also illustrates one way to recognize resonance - when it is possible to draw two or more equivalent Lewis structures. If we were to draw the structure of an aromatic molecule such as 1,2-dimethylbenzene, there are two ways that we could draw the double bonds:
Which way is correct? There are two simple answers to this question: 'both' and 'neither one'. Both ways of drawing the molecule are equally acceptable approximations of the bonding picture for the molecule, but neither one, by itself, is an accurate picture of the delocalized pi bonds. The two alternative drawings, however, when considered together, give a much more accurate picture than either one on its own. This is because they imply, together, that the carbon-carbon bonds are not double bonds, not single bonds, but about halfway in between.
When it is possible to draw more than one valid structure for a compound or ion, we have identified resonance contributors: two or more different Lewis structures depicting the same molecule or ion that, when considered together, do a better job of approximating delocalized pi-bonding than any single structure. By convention, resonance contributors are linked by a double-headed arrow, and are sometimes enclosed by brackets:
In order to make it easier to visualize the difference between two resonance contributors, small, curved arrows are often used. Each of these arrows depicts the ‘movement’ of two pi electrons. In the drawing of resonance contributors, however, this electron ‘movement’ occurs only in our minds, as we try to visualize delocalized pi bonds. Nevertheless, use of the curved arrow notation is an essential skill that you will need to develop in drawing resonance contributors.
The depiction of benzene using the two resonance contributors A and B in the figure above does not imply that the molecule at one moment looks like structure A, then at the next moment shifts to look like structure B. Rather, at all moments, the molecule is a combination, or resonance hybrid of both A and B.
It is very important to be clear that in drawing two (or more) resonance contributors, we are not drawing two different molecules: they are simply different depictions of the exact same molecule. Furthermore, the double-headed resonance arrow does NOT mean that a chemical reaction has taken place.
Benzene is often drawn as only one of the two possible resonance contributors (it is assumed that the reader understands that resonance hybridization is implied). However, sometimes benzene will be drawn with a circle inside the hexagon, either solid or dashed, as a way of drawing a resonance hybrid.
Molecules with a Single Resonance Configuration
Example 1
Example 2
Example 3
Example 4
The above resonance structures show that the electrons are delocalized within the molecule and through this process the molecule gains extra stability. Ozone with both of its opposite formal charges creates a neutral molecule and through resonance it is a stable molecule. The extra electron that created the negative charge one terminal oxygen can be delocalized by resonance through the other terminal oxygen.
Benzene is an extremely stable molecule due to its geometry and molecular orbital interactions, but most importantly, due to its resonance structures. The delocalized electrons in the benzene ring make the molecule very stable and with its characteristics of a nucleophile, it will react with a strong electrophile only and after the first reactivity, the substituted benzene will depend on its resonance to direct the next position for the reaction to add a second substituent.
Molecules and ions with more than one resonance form:
Some structural resonance conformations are the major contributor or the dominant forms that the molecule exists. For example, if we look at the above rules for estimating the stability of a molecule, we see that for the third molecule the first and second forms are the major contributors for the overall stability of the molecule. The nitrogen is more electronegative than carbon so, it can handle the negative charge more than carbon. A carbon with a negative charge is the least favorable conformation for the molecule to exist, so the last resonance form contributes very little for the stability of the Ion.
Hybrid Resonance
The different resonance forms of the molecule help predict the reactivity of the molecule at specific sites.
The Hybrid Resonance forms show the different Lewis structures with the electron been delocalized. This is very important for the reactivity of chloro-benzene because in the presence of an electrophile it will react and the formation of another bond will be directed and determine by resonance. The lone pair of electrons delocalized in the aromatic substituted ring is where it can potentially form a new bond with an electrophile, as it is shown there are three possible places that reactivity can take place, the first to react will take place at the para position with respect to the chloro- substituent and then to either ortho- position.

