Molecular Geometry Overview
- Page ID
- 55230
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The specific three dimensional arrangement of atoms in molecules is referred to as molecular geometry. We also define molecular geometry as the positions of the atomic nuclei in a molecule. There are various instrumental techniques such as X-Ray crystallography and other experimental techniques which can be used to tell us where the atoms are located in a molecule. Using advanced techniques, very complicated structures for proteins, enzymes, DNA, and RNA have been determined. Molecular geometry is associated with the chemistry of vision, smell and odors, taste, drug reactions and enzyme controlled reactions to name a few.
It is common practice to represent bonding patterns by "generic" formulas such as \(AX_4\), \(AX_2E_2\), etc., in which "X" stands for bonding pairs and "E" denotes lone pairs. This convention is known as the "AXE Method."
Molecular geometry is associated with the specific orientation of bonding atoms. A careful analysis of electron distributions in orbitals will usually result in correct molecular geometry determinations. In addition, the simple writing of Lewis diagrams can also provide important clues for the determination of molecular geometry. Click on a picture to link to a page with the GIF file and a short discussion of the molecule.
| Steric Number (# bonded atoms + # electron pairs) | ||||
| 6 | 5 | 4 | 3 | 2 |
AX6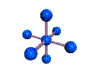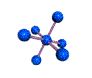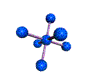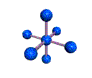 octahedral |
AX5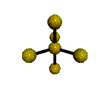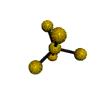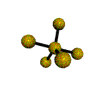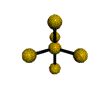 trigonal bipyramidal |
AX4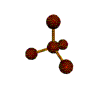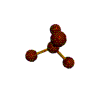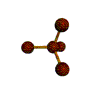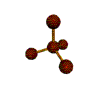 tetrahedral |
AX3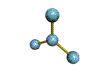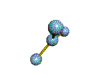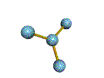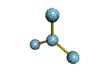 trigonal planar |
AX2 linear |
| 1 lone pair of electrons | ||||
AX5E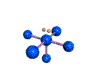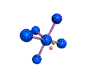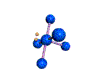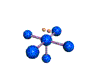 square pyramidal |
AX4E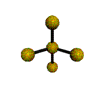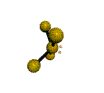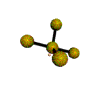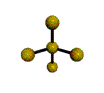 distorted tetrahedron |
AX3E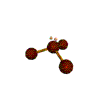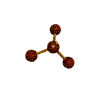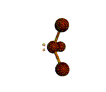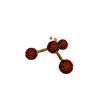 pyramidal |
AX2E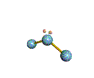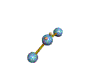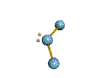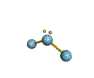 nonlinear |
AXE linear |
| 2 lone pairs of electrons | ||||
AX4E2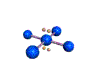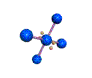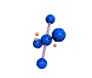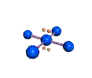 square planar |
AX3E2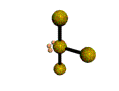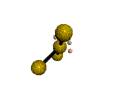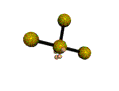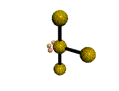 T-shaped |
AX2E2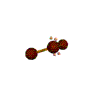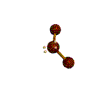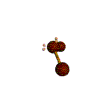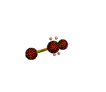 bent |
AXE2 linear |
|
| 3 lone pairs of electrons | ||||
| AX3E3 T-shaped |
AX2E3 linear |
AXE3 linear |
||
| 4 lone pairs | ||||
| AX2E4 linear |
AXE4 linear |
|||
| 5 lone pairs | ||||
| AXE5 linear |
||||
Valence Shell Electron Pair Repulsion (VSEPR) theory
Electron pairs around a central atom arrange themselves so that they can be as far apart as possible from each other. The valence shell is the outermost electron-occupied shell of an atom that holds the electrons involved in bonding. In a covalent bond, a pair of electrons is shared between two atoms. In a polyatomic molecule, several atoms are bonded to a central atom using two or more electron pairs. The repulsion between negatively charged electron pairs in bonds or as lone pairs causes them to spread apart as much as possible.
The idea of "electron pair repulsion can be demonstrated by tying several inflated balloons together at their necks. Each balloon represents an electron pair. The balloons will try to minimize the crowding and will spread as far apart as possible. According to VSEPR theory, molecular geometry can be predicted by starting with the electron pair geometry about the central atom and adding atoms to some or all of the electron pairs. This model produces good agreement with experimental determinations for simple molecules. With this model in mind, the molecular geometry can be determined in a systematic way.
- Lewis diagrams provide information about what atoms are bonded to each other and the total electron pairs involved.
- Electron pair geometry is determined from the total electron pairs.
Molecules can then be divided into two groups:
- Group 1: Molecules with NO lone electron pairs. In this case the molecular geometry is identical to the electron pair geometry.
- Group 2: Molecules with one or more lone electron pairs. In this case an extra step is needed to to translate from electron pair geometry to the final molecular geometry, since only the positions of bonded atoms are considered in molecular geometry.
Outside Links
- Pfennig, Brian W.; Frock, Richard L. "The Use of Molecular Modeling and VSEPR Theory in the Undergraduate Curriculum to Predict the Three-Dimensional Structure of Molecules." J. Chem. Educ.1999 76 1018.
- Covalent Radii - Wikipedia: http://en.Wikipedia.org/wiki/Covalent_radius
Contributors and Attributions
- Charles Ophardt, Professor Emeritus, Elmhurst College; Virtual Chembook
- Robyn Rindge (Class of '98) who now works for PDI Dreamworks (look for his name in the credits of Shrek2.). Robyn drew these rotating molecules using Infini-D (MetaCreations).
- Paul Groves, chemistry teacher at South Pasadena High School and Chemmy Bear