1.2: Chemical Bonding

The electronic configurations of the elements, as specified in the previous chapter, apply in principle only to isolated atoms - atoms separated by distances over which no mutual interactions of their electronic orbitals can occur (infinite distance). This condition is never met in condensed phases (i.e., liquids and solids); it is only encountered in high vacua where atoms move over long distances without mutual interaction. Under normal conditions, particularly in the mentioned condensed phases, atoms are separated over distances controlled, in essence, by the dimension of their respective outermost occupied electronic orbitals. Whenever the outer electron shells of two or more atoms come in contact with each other (overlap to any extent), the potential for interaction (reaction) exists. Spontaneous reaction (consisting of a rearrangement of the electronic orbitals and/or actual transfer of electrons from one atom to another) will take place whenever such a rearrangement results in a lower energy configuration. This means that the driving force for mutual interaction and rearrangement of electronic configurations is in most instances (but not always) manifested through the release of heat (a form of energy) to the environment. [Typical case: \(\mathrm{Mg}+1 / 2 \mathrm{O}_{2} \rightarrow\) Reaction Product \((\mathrm{MgO})+(\) light + heat) i.e. energy.] Since the same amount of energy must be supplied to the system if the original state - i.e., separation of the species – is to be reestablished, the reaction partners are “bonded together” by comparable energies. The “strength” of the bonds can obviously vary from system to system with the nature of the electronic rearrangement.

Even the inert gases, particularly the heavier ones like xenon, are capable of forming associations with other atoms. Sometimes we find that two atoms assume a more stable state by sharing electrons; at other times, an atom may transfer electrons to another atom in order to achieve a greater stability. In still other instances, the rearrangement may simply be an orbital distortion or an internal charge redistribution. In either event the mutual benefit that accrues is the formation of what is commonly called a chemical bond. Through these bonds atoms combine with each other to form very different kinds of particles referred to as molecules and ions.

NATURE OF CHEMICAL BONDS

In order for a chemical bond to be formed between two atoms, there must be a net decrease in the energy of the system (the two atoms): the ions or molecules produced by electronic rearrangements must be in a lower energy state than the atoms were prior to interaction, prior to bond formation.

Since atoms of each of the elements have different electronic structures, the variety of possible chemical bonds (differing from each other in at least some small way) is considerable and is even further increased by the effects of neighboring atoms on the bond under consideration. The modes of bond formation can be categorized into two basic types, each representing a type of bonding. The bonding types are called electrovalent (or ionic) bonding and covalent bonding. Electrovalent bonding arises from complete transfer of one or more electrons from one atom to another; covalent bonding arises from the sharing of two or more electrons between atoms. Since these models represent the limiting cases, we can anticipate that most real bonds will fall between these two extremes. (Two additional types of bonding, metallic bonding and Van der Waals bonding, will be discussed later.)

Before discussing these models in detail it is appropriate to consider the relationships between the electronic structures of atoms and their chemical reactivity. The inert gases (Group VIII) are the most stable elements with regard to bond formation, i.e. toward electronic rearrangements. It is therefore useful to examine the reasons for their stability. Inert gases all have electronic structures consisting of filled subshells. For all but helium the outer (or valence) shell contains eight electrons, with filled \(s\) and \(p\) sublevels \(\left(n s^{2} p^{6}\right)\). The electronic structure of helium is \(1 s^{2}\), which is equivalent to the structure of the other inert gases since there is no \(1 \mathrm{p}\) sublevel. Inert gases have high ionization energies because each electron in the sublevel of highest energy is poorly screened from the nucleus by other electrons in its same sublevel. Each electron "sees" relatively high positive charge on the nucleus, and a large amount of energy is required to remove it from the atom. Inert gases have very low electron affinity because any added electron must enter a significantly higher energy level. We find, therefore, that the electronic structures of inert gases are particularly resistant to changes by either loss or gain of electrons and, further, that atoms of other elements with fewer or more electrons than inert gas configuration tend to gain or lose electrons, respectively, to achieve such inert gas structure.

ELECTROVALENT (IONIC) BONDING

An electrovalent bond is formed by the transfer of one or more electrons from one atom to another. Consider first atoms that have electronic structures differing from an inert gas structure by only a few, (1, 2 or 3) electrons. These include the representative elements of Groups I, II and III in the Periodic Table, which have respectively 1, 2 and 3 electrons more than a neighboring inert gas, and the representative elements of Groups V, VI and VII, which have respectively 3, 2 and 1 electrons less than a neighboring inert gas (fig. 1).

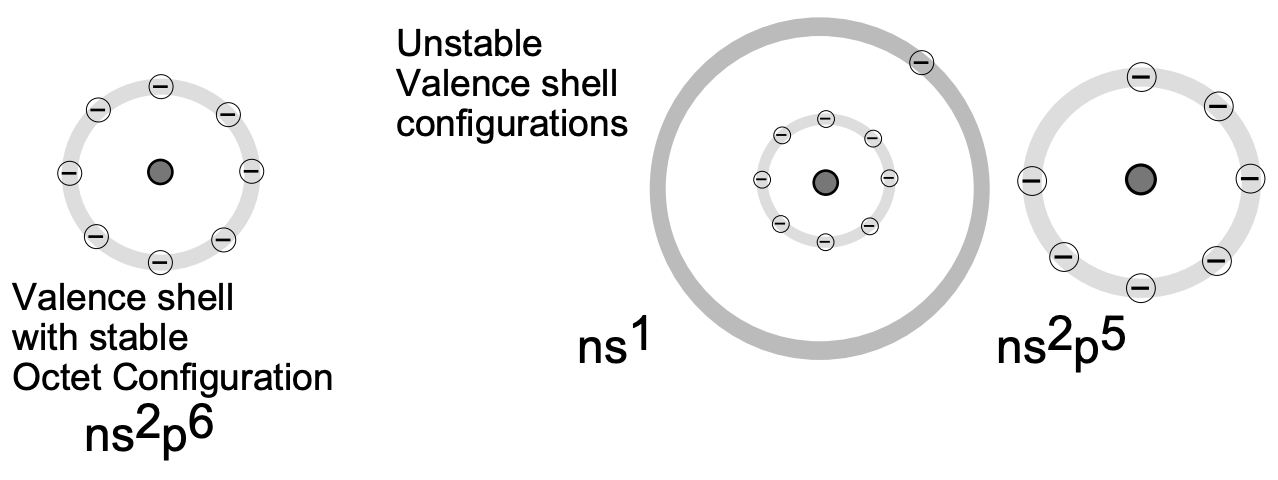
Fig.1 Stable and Unstable Valence Shell Configurations.

The elements of Groups I, II and III can form the electronic structure of an inert gas by losing their outer 1, 2 and 3 (valence) electrons. (The resulting species are positively charged ions.)

In a similar electron transfer which, however, involves the acquisition of electrons in the outer valence levels, elements of Groups V, VI and VII form an inert gas electronic structure (by formation of negatively charged ions).

It is through the electron transfer between an electron-losing element and an electron-gaining element that compounds are formed which involve electrostatic attraction (electrovalent bonds) of oppositely charged species called ions.

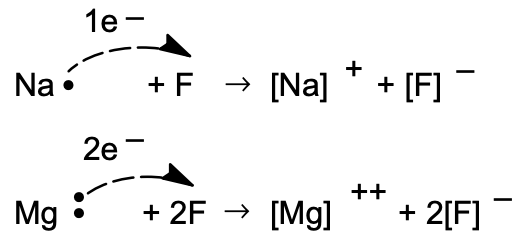
(In the notation [Na•], the dot indicates the outermost electron which is in excess of the rare gas configuration. It is referred to as a valence electron.)

Elements immediately following the inert gases (in the horizontal columns of the Periodic Table) lose electrons, and those immediately preceding the inert gases gain electrons on interaction. The resulting compounds are called electrovalent; the valence number (charge on the ion) of a particular element when it forms an electrovalent compound is given by the number of electrons lost or gained in changing from the atomic to the ionic state.

The stoichiometric formula of an electrovalent compound reflects the ratio (usually very simple) of positive to negative ions that gives a neutral aggregate. Hence, the ions \(\mathrm{Na}^{+}\) and \(\mathrm{F}^{-}\) form a compound whose formula is \(\mathrm{NaF}\) because these ions are singly charged and are present in the compound in a one-to-one ratio. Magnesium nitride, composed of \(\mathrm{Mg}^{2+}\) and \(\mathrm{N}^{3-}\), has the formula \(\mathrm{Mg}_{3} \mathrm{~N}_{2}\) because this composition represents electroneutrality.

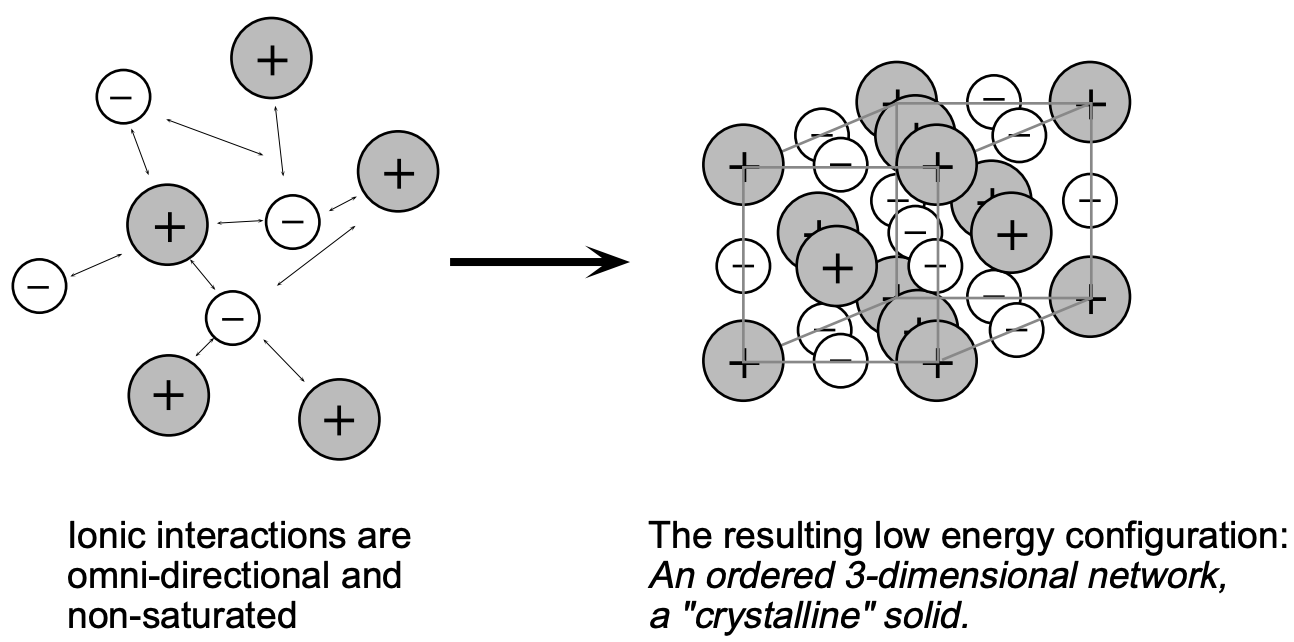
The electrovalent bond is the result of electrostatic attraction between ions of opposite charge. This attractive force accounts for the stability of these compounds, typified by \(\mathrm{NaF}, \mathrm{LiCl}, \mathrm{CaO}\), and \(\mathrm{KCl}\). The ions individually possess the electronic structures of neighboring inert gases; their residual charge arises from an imbalance in the number of electrons and protons in their structures. Isolated ions and simple isolated pairs of ions, as represented by the formula \(\mathrm{NaCl}\), exist only in the gaseous state. Their electrostatic forces are active in all directions; they attract oppositely charged species and thus can form regular arrays, resulting in ordered lattice structures, i.e. the solid state (fig. 2). Even in the liquid state and in solutions (where disruptive thermal forces reach values close to that of the attractive electrostatic bonding forces) attraction between ions and with other species remains effective.

Figure 2 Formation of a crystalline, ordered body (a SOLID), a direct consequence of ion interaction in conjunction with energy minimization..

Energetics of Ionic Bonding

Ionic bonding is the simplest type of chemical bonding to visualize, since it is totally (or almost totally) electrostatic in nature. The principle of the energetics of ionic bond formation is realized when considering the formation of \(\mathrm{NaCl}\) (our common salt) from its constituents \(\mathrm{Na}\) (metal) and \(\mathrm{Cl}_{2}\) (chlorine gas). Formally, this reaction is:

\begin{aligned}
&\mathrm{Na}(\mathrm{s})+1 / 2 \mathrm{Cl}_{2}(\mathrm{~g}) \rightarrow \mathrm{NaCl}(\mathrm{s}) \\
&\Delta \mathrm{H}=-414 \mathrm{~kJ} / \mathrm{mol}
\end{aligned}

The equation as written indicates that 1 mole sodium reacts with \(1 / 2\) mole chlorine \(\left(\mathrm{Cl}_{2}\right)\) under formation of 1 mole (ionically bonded) sodium chloride; this reaction is accompanied by the release \((-)\) of \(414 \mathrm{~kJ}\) of energy \((\Delta \mathrm{H})\), referred to as the heat of reaction. From earlier considerations it is clear that electronic rearrangement (reaction or bond formation) takes place because the resulting solid product \((\mathrm{NaCl})\) is at a lower energy state than the sum total of the energies of the original components.

The energetics associated with ionic bond formation may be determined quantitatively by considering the energy changes associated with the individual steps leading from the starting materials to the final product (Haber-Born cycle).

The bond formation in NaCl may be formally presented as an electron-transfer reaction:

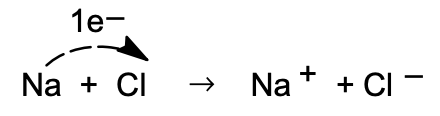
The reactions involved in this process which result in the formation of 1 mole of solid salt are:

(1) Ionization of \(\mathrm{Na}\):

\(\mathrm{Na}\) (gas) \(\rightarrow \mathrm{Na}^{+}+1 \mathrm{e}\) (E.I. \(=+497 \mathrm{~kJ} / \mathrm{mole})\)

The energy change associated with this step, energy of ionization (E.I.), is

\(+497 \mathrm{~kJ} /\) mole.

(2) Acquisition of one electron by \(\mathrm{Cl}\):

\(\mathrm{Cl}\) (gas) \(+1 \mathrm{e} \rightarrow \mathrm{Cl}^{-}\) (E.A. \(=-364 \mathrm{~kJ} / \mathrm{mole}\))

The energy change associated with this step, electron affinity (E.A.), is \(-364 \mathrm{~kJ} / \mathrm{mole}\). The minus sign reflects an energy release, a lowering of the energy state associated with the achievement of stable rare gas configuration by chlorine.

So far, the energy balance appears positive ( \(\Delta \mathrm{E}=+133 \mathrm{~kJ}\) ); this means the reaction is not favored since the final products are at a higher energy state than the starting products. However, there are additional steps involved since:

(3) Vaporization of \(\mathrm{Na}\):

\(\mathrm{Na}\) (metal) \(\rightarrow \mathrm{Na}\) (gas) \(\left(\Delta \mathrm{H}_{\mathrm{V}}=+109 \mathrm{~kJ} /\right.\) mole)

The energy required to transform \(\mathrm{Na}\) (metal) into \(\mathrm{Na}\) (gas), the latent heat of vaporization \(\left(\Delta \mathrm{H}_{\mathrm{v}}\right)\), is \(109 \mathrm{~kJ} /\) mole (now reaction appears even less favorable).

(4) Dissociation of \(\mathrm{Cl}_{2}\):

\(\mathrm{Cl}_{2} \rightarrow 2 \mathrm{Cl} \quad(\text { E.D. }=+242 \mathrm{~kJ} \text { ) }\)

The energy associated with breaking up the (stable) chlorine molecule into two reactive chlorine atoms, dissociation energy (E.D.), is \(+242 \mathrm{~kJ} / \mathrm{mole}\). (Since the formation of one mole \(\mathrm{NaCl}\) involves only 1 mole \(\mathrm{Cl}\), and since 2 moles are formed from one mole \(\mathrm{Cl}_{2}\), the energy required in this step is \(1 / 2 \mathrm{E} . D\)., or \(121 \mathrm{~kJ}\).)

The total energy change associated with reactions (1) through (4), \(\Delta \mathrm{H}_{\mathrm{T}}=+364 \mathrm{~kJ}\) This indicates that one or more basic reactions which lead to an overall decrease in energy are still unconsidered.

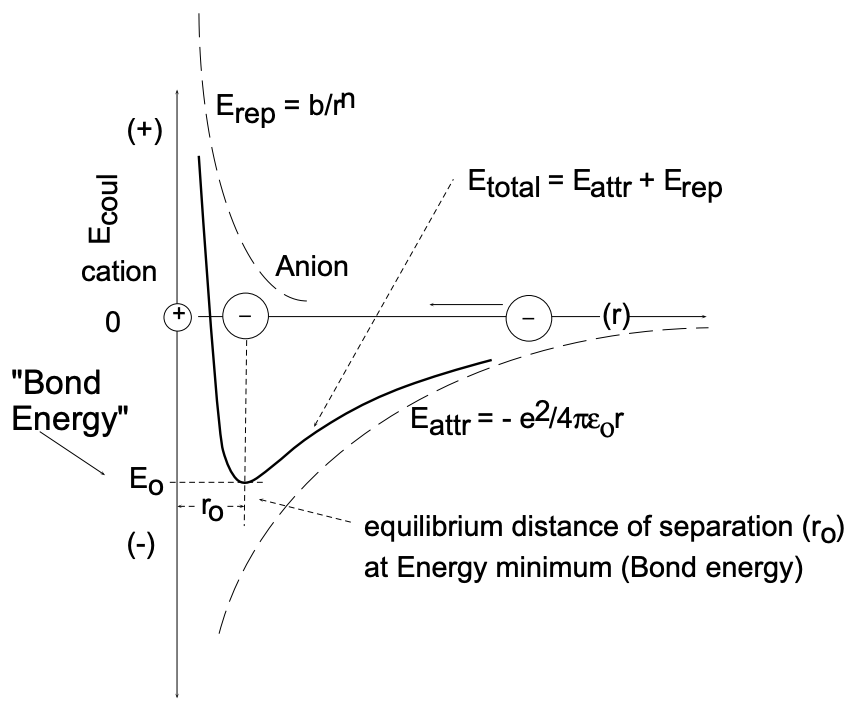
(5) Unconsidered as yet is the coulombic attraction of the reaction products which are of opposite charge and an energy term associated with the formation of the "solid state" product, \(\mathrm{NaCl}\). The two ionic species, originally at zero energy (infinite distance of separation), attract each other with an accompanying energy change (decrease).

The energetics associated with the approach of the reaction partners (fig. 3) is best considered by fixing the position of one, for example \(\mathrm{Na}^{+}\), and letting the other \(\left(\mathrm{Cl}^{-}\right)\) approach: as \(\mathrm{Cl}^{-}\) approaches \(\mathrm{Na}^{+}\), E decreases according to Coulomb's law with \(\mathrm{e}^{2} / 4 \pi \varepsilon_{0} r\). With the approach of the two oppositely charged ions, the outermost electronic shells will come into contact and a repulsive force will become active as the shells interpenetrate. The repulsive force \(\left(E_{\text {rep }}\right)\) increases with \(+b / r^{12}\) and thus is only active in the immediate vicinity of the sodium ion, but at that stage increases rapidly. The two ions at close proximity are under the influence of both attractive and repulsive forces and will assume a distance of separation at which the two forces balance each other - a distance which is referred to as the equilibrium separation (\(r_o\)) and which corresponds to the energy minimum for the NaCl molecules:

\(E_{\text {coul }}=-\dfrac{e^{2}}{4 \pi \varepsilon_{0} r_{0}}+\dfrac{b}{r_{0}^{12}}\)

where \(e=\) electronic charge, \(\varepsilon_{0}=\) permittivity of free space \(\left(8.85 \times 10^{-12} \mathrm{~F} / \mathrm{m}\right)\) and \((\mathrm{b})\) is a constant. ( \(r_{0}\) for gaseous molecules may be obtained from physical measurements.)

Figure 3 Energetics of ionic bonding.

If the presently considered coulombic (attractive) energy term is taken into consideration as reaction (5), it will decrease the overall positive energy change, \(\Delta \mathrm{H}_{\bar{T}}\); it will, however, not make it change sign from (+) to (-). Thus, \(\mathrm{NaCl}\) molecules in gaseous form are not the final reaction product; nor would reaction occur if \(\Delta \mathrm{H}_{\mathrm{T}}\) remained positive.

Considering an ionically bonded, gaseous \(\mathrm{Na}^{+} \mathrm{Cl}^{-}\) molecule, it is clear that its electrostatic forces \((+)\) and \((-)\) are not saturated - they remain active in all possible directions. This means that \(\mathrm{Cl}^{-}\) will attract \(\mathrm{Na}^{+}\) ions from other directions as will the \(\mathrm{Na}^{+}\) atoms attract additional \(\mathrm{Cl}^{-}\) ions. The result of these attractive forces in all directions is the formation of a "giant size" ionic body - a "solid" body of macroscopic dimensions. From the preceding it is recognized that the minimum energy configuration is given by a body in which \(\mathrm{Na}^{+}\) and \(\mathrm{Cl}^{-}\) are arranged with extreme periodicity and order since any ion located outside of its "equilibrium position" will be in a "higher energy configuration"; such an ordered body is referred to as a crystalline solid, or frequently just called a solid (fig. 2).

The total energy change associated with the formation of one mole of crystalline ionic solid from its ionic constituents is given as:

\(\mathrm{E}_{\text {cryst }}=-\dfrac{M \mathrm{~N}_{\mathrm{A}} \mathrm{e}^{2}\left(\mathrm{Q}_{1} \mathrm{Q}_{2}\right)}{4 \pi \varepsilon_{0} r_{o}}\left(1-\dfrac{1}{\mathrm{n}}\right)\)

where \(\mathrm{M}=1.747\) ("Madelung" constant for \(\mathrm{NaCl}\), reflecting multiple interactions for the particular geometric arrangement of ions in the solid), \(\mathrm{N}_{\mathrm{A}}=\) Avogadro's number, \(\mathrm{Q}=\) number of charges per ion ( 1 for \(\mathrm{Na}^{+}\) and \(\left.\mathrm{Cl}^{-}\right), \mathrm{r}_{0}=\) equilibrium distance of separation of ions, and \(n=\) repulsive exponent \((n=12\) for \(\mathrm{NaCl})\).

[The relationship for the crystal energy \(\left(\Delta \mathrm{E}_{\text {cryst }}\right)\) is readily obtained from equilibrium energy considerations:

\(\mathrm{E}_{\text {coul }}=-\dfrac{\mathrm{e}^{2}}{4 \pi \varepsilon_{0} r}+\dfrac{\mathrm{b}}{4 \pi \varepsilon_{0} r^{n}}\)

At equilibrium distance of ion separation \(\left(r_{0}\right),(\mathrm{dE} / \mathrm{dr})=0\). Thus:

\(\left(\dfrac{d E}{d r}\right)_{r_{0}}=\dfrac{e^{2}}{4 \pi \varepsilon_{0} r_{o}^{2}}-\dfrac{n b}{4 \pi \varepsilon_{0} r_{o}^{n+1}}=0\)

and

\(\mathrm{b}=\dfrac{\mathrm{e}^{2} \mathrm{r}_{\mathrm{o}}^{\mathrm{n}-1}}{\mathrm{n}}\)

and

\begin{aligned}
&E_{o(\text { Coul })}=-\frac{e^{2}}{4 \pi \varepsilon_{o} r_{o}}+\frac{e^{2}}{n 4 \pi \varepsilon_{o} r_{o}} \\
&E_{o(\text { Coul })}=-\frac{e^{2}}{4 \pi \varepsilon_{o} r_{o}}\left(1-\frac{1}{n}\right)
\end{aligned}

For a "molar" crystal with ionic charges \(\mathrm{Q}_{1}\) and \(\mathrm{Q}_{2}\), the molar \(\Delta \mathrm{E}_{\mathrm{o}(\text { Coul) }}\) is thus given as:

\(\Delta \mathrm{E}_{\text {cryst }}=-\dfrac{\mathrm{MN}_{\mathrm{A}} \mathrm{Q}_{1} \mathrm{Q}_{2} \mathrm{e}^{2}}{4 \pi \varepsilon_{\mathrm{o}} \mathrm{r}_{\mathrm{o}}}\left(1-\dfrac{1}{\mathrm{n}}\right)\)

Here \(M\) and \(N_{A}\) stand, as indicated above, for the conventional terms, the Madelung constant and Avogadro's number.]

For the present system ( \(\mathrm{NaCl})\) :

\(\Delta \mathrm{E}_{\text {cryst }}=-777 \mathrm{~kJ} /\) mole.

Now considering reactions (1) through (5):

\(\Delta \mathrm{H}_{\text {Total }}=-414 \mathrm{~kJ} /\) mole

which is identical with the value experimentally determined and given for the reaction:

\begin{aligned}
&\mathrm{Na}(\text { metal })+\mathrm{Cl}_{2} \text { (gas) } \rightarrow \mathrm{NaCl} \text { (solid) } \\
&\Delta \mathrm{H}_{\text {Reaction }}=-414 \mathrm{~kJ} / \text { mole }
\end{aligned}

In the Haber-Born cycle, the reaction energy \((\Delta \mathrm{H})\) associated with the formation of \(\mathrm{NaCl}\) from \(\mathrm{Na}+\mathrm{Cl}_{2}\) may be summarized as:

\(\Delta \mathrm{H}=\text { E.I. }+\text { E.A. }+\Delta \mathrm{H}_{\mathrm{V}}+1 / 2 \text { E.D. }+\Delta \mathrm{H}_{\text {cryst }}\)

\(\Delta \mathrm{H}\), the heat of reaction, may thus be obtained from the energetics of the steps leading to the end product. In most instances, however, the reaction energy \((\Delta \mathrm{H})\) is determined experimentally in a calorimeter and the Haber-Born cycle is used to obtain the value of \(\Delta \mathrm{E}_{\text {cryst }}\) or \(\mathrm{E} . \mathrm{A} .\), which are both extremely hard to come by.

Conclusions: A primary drive for atomic interactions leading to "bonding" is the achievement of valence shell octets which exhibit a high degree of stability. If atoms on the left and right side of the Periodic Table interact, i.e. atoms with a large difference in electron affinity ( \(\triangle \mathrm{E} . \mathrm{A} .)\), stabilization is achieved by electron octet formation through charge transfer. The reaction products exhibit opposite charges ( \(\oplus\) cations, \(\ominus\) anions) and are subject to Coulombic attraction - ionic bonds are formed. Since the electrostatic forces are non-directional and non-saturated, energy minimization will result in the formation of macroscopic bodies that are highly ordered on the atomic scale, crystalline ionic solids. Ionic solids have mostly predictable, basic properties:

• atomic arrangements are a function of the ion size ratio, the charge ratio of ions, and their electronic structure;
• electrical and thermal conductivities are expected to be low because the high stability of the octets formed results in bound electrons which do not contribute to conduction (there is a large "energy gap" to be crossed for electrons to move into a higher energy state);
• optically, ionic solids are mostly transparent, or translucent, reflecting octet stability of the electrons and macro- or micro-crystallinity;
• melting points are high, increasing with the electronic charges on the cations and anions;
• ionic solids are normally hard and brittle.

COVALENT BONDING

Mechanical Concepts and Conclusions

In 1924 L. DeBroglie advanced the hypothesis that all matter in motion possesses wave properties and can be attributed a particle wavelength

\(\lambda_{P}=\mathrm{h} / \mathrm{mv}\)

where \(\mathrm{h}\) is the Planck constant, \(\mathrm{m}\) is the mass of the matter and \(v\) is its velocity.

The credibility of this hypothesis was established by Davisson and Germer in 1927 when they demonstrated that electrons (like electromagnetic radiation) are diffracted by crystal lattices. An important consequence of the dual nature of matter (it exhibits both particle and wave properties) is the uncertainty principle established in 1927 by W. Heisenberg. It states that it is impossible to simultaneously know with certainty both the momentum and position of a moving particle:

\(\left(\Delta p_{x}\right)(\Delta x) \gtrsim h\)

We can paraphrase the uncertainty principle in the following manner: If the energy of a particle is known (measured) with high precision, its location is associated with a high degree of uncertainty.

If electrons occupied simple orbits (as postulated by Bohr-Sommerfeld), their momentum and position could be determined exactly at any moment - in violation of the uncertainty principle. According to Heisenberg, if the energy of an electron is specified with precision (sharpness of spectral lines), its location can only be specified in terms of the probability of finding this electron in a certain location (volume element). These arguments give rise to the concepts of probability density and electron cloud which are inherent to the wave-mechanical electron concept emanating from the solutions of Schrödinger’s wave equation which relates the energy of an orbiting electron to its wave properties. When solving exactly the Schrödinger wave equation for an electron in a hydrogen atom, a quantization results according to which electrons can only assume certain energies which are in quantitative agreement with those obtained from the Bohr theory.

In comparison to the Bohr theory, significant differences are observed for the orbital quantization (orbital quantum number \(I\) ) which specifies the orbital shape. For \(n=1\), \(I=0\) (1s orbital), wave mechanics predicts a spherical electron density distribution with a maximum probability density \(\left(\psi^{2}\right)\) at a distance of \(0.529 \AA\left(\mathrm{a}_{0}\right)\) from the nucleus. For \(I=1\) (p orbitals), however, it is found that the orbitals (three) form lobes aligned with rectangular coordinates (see LN-1, fig. 3). For \(I=2\) (d orbitals), five complex orbital configurations are obtained.

Previous considerations suggest that all elements attempt to assume a stable octet configuration with eight electrons in the valence shell. (For hydrogen, with only one shell occupied, the stable configuration consists of two electrons in the \(\mathrm{K}\) shell - which is the maximum number of electrons that can be accommodated.) Stable octet formation is possible through electron transfer (and ionic bond formation) when, for example, elements in columns IA, IIA and IIIA react with elements in columns VA, VIA and VIIA, respectively. In these instances, the reaction partners exhibit rather pronounced differences in electron affinity and upon reaction one assumes octet configuration by losing one or more electrons while the other does so by acquiring the missing number of electrons.

This mechanism is clearly not possible if \(\mathrm{H}\) reacts with \(\mathrm{H}\) to form an \(\mathrm{H}_{2}\) molecule where two atoms are bonded together. The same argument holds for the formation of \(\mathrm{N}_{2}, \mathrm{Cl}_{2}\) and \(\mathrm{O}_{2}\) molecules. Inert gas configuration (octet configuration) in such elements is achieved by a mechanism called orbital sharing and the resulting bond is called covalent, or electron-pair bond.

A covalent bond is somewhat more difficult to visualize than an ionic or electrovalent bond because it involves the sharing of a pair of electrons between atoms. The stability of this bond can be attributed to the complex mutual attraction of two positively charged nuclei by the shared pair of electrons. In principle, the bond can be understood if it is recognized that both electrons in the bonding orbital spend more time between the two nuclei than around them and thus must exercise attractive forces which constitute the bond. In this arrangement it is clear that each electron, regardless of its source, exerts an attractive force on each of the “bonded” nuclei. The pair of electrons in a covalent bond is unique to the extent that the Pauli exclusion principle precludes the presence of additional electrons in the same orbital. Furthermore, the pairing phenomenon neutralizes the separate electronic spins of the single electrons, and the resulting electron pair with its zero spin momentum interacts less strongly with its surroundings than do two independent electrons. [Covalent bonds are conveniently symbolized through the dot notation, introduced first by Lewis (fig. 4).]

LEWIS NOTATION:

In LEWIS notation the covalent molecular bond is indicated as a BAR or as two DOTS (standing for the paired electrons)

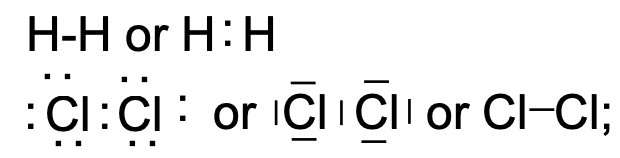
Formal valence shell octet stabilization can be achieved by electron sharing, H whereby one electron from each reaction partner share - spin paired - the molecular bonding orbital.

Quantum mechanics makes it possible to rigorously describe these bonds for very simple cases such as the hydrogen molecule, which is composed of two protons and two electrons. It can thus be shown that the potential energy for the system reaches a minimum for a certain equilibrium distance between the nuclei, with increased electron density between the nuclei. At shorter distances between the nuclei repulsive forces are found to increase very rapidly.

In the hydrogen molecule \(\left(\mathrm{H}_{2}\right)\), the two hydrogen atoms are effectively linked together by one molecular electron orbital, termed a \(\sigma\) orbital, which comprises both atoms and contains two electrons. (fig. 5) Each of these two electrons can be considered to have originated from one of the two atoms - they were originally both \(1 \mathrm{~s}\) electrons with the same spin value \((s=+1 / 2)\). In the molecular orbit comprising both atoms, the spins of

Figure 5 Covalent bond formation

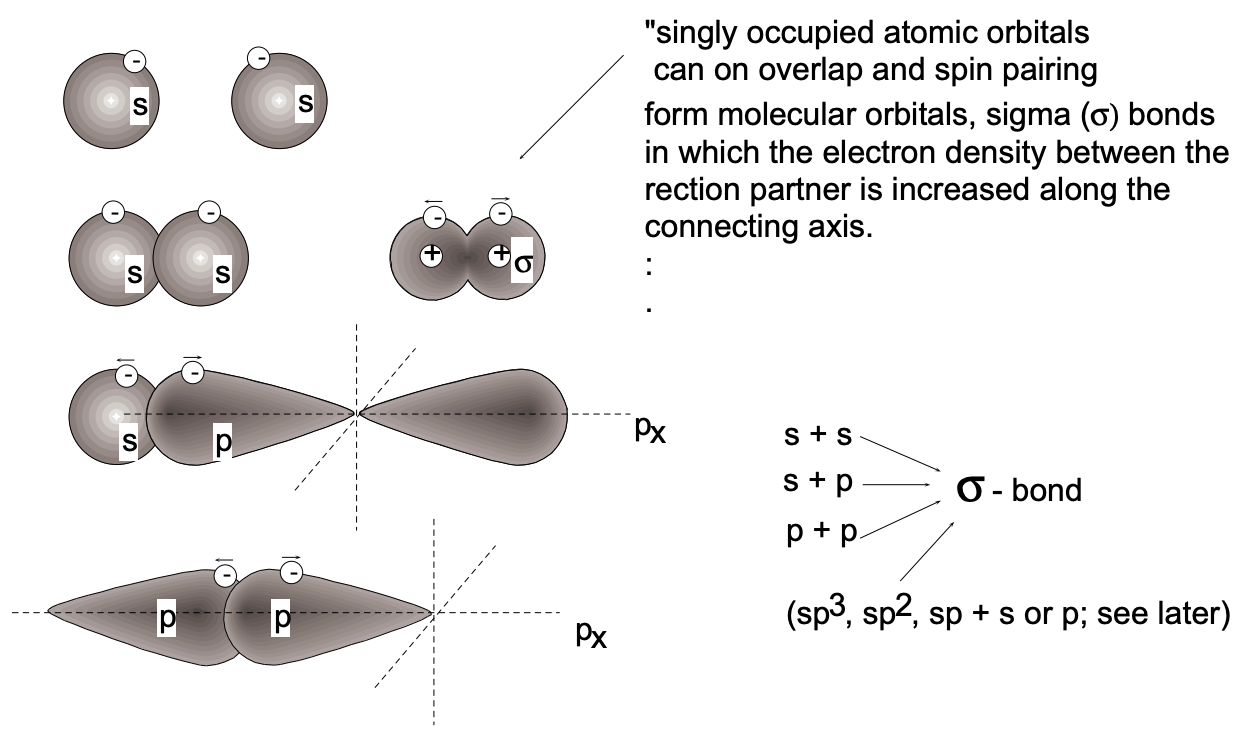
the two electrons must align anti-parallel (opposite spin). This spin-pairing process results in a considerable release of energy and thus contributes significantly to the stability (strength) of the covalent bond formed. It is interesting that according to Newtonian mechanics, no stable configuration can arise from the placement of two electrons into the same region (orbit) - wave mechanics (see below), however, predicts increased stability from such configurations. (Similar spin-pairing occurs in the filling of atomic orbitals.) In the molecular case, spin-pairing has the consequence that both the probability distributions \(\left(\psi^{2}\right)\) and spatial distribution of electrons are such that maximum overlap of orbitals of combining atoms occurs.

The bond formed in hydrogen is a single bond, containing two electrons with paired spins. This formulation predicts that there will be a fixed internuclear separation which, for the hydrogen molecule, has the value of \(0.74 \AA\). [ \(\sigma\) bonds are formed not only by s orbital overlap, but also by p-s and p-p orbital overlap as well as by the overlap of \(s\) or \(p\) orbitals with hybridized orbitals; to be discussed below (see fig. 5).]

It is important to recognize that octet stabilization by electron orbital sharing results in bond properties which differ fundamentally from those encountered in ionic (electrovalent) bonding: with the formation of the covalent bond between the hydrogen atoms \(\left(\mathrm{H}_{2}\right.\) molecule formation) the bond forming capabilities of the two hydrogen atoms are saturated; the final product is a distinct molecule \(\left(\mathrm{H}_{2}\right)\) rather than a giant-sized solid body which is obtained as the final product with ionic bond formation. Covalent solid bodies, however, also do exist: they are formed if the elements involved have the capability of forming more than one bond. For example, carbon will form four covalent bonds in tetrahedral configuration - the result is diamond, a covalently bonded, three dimensional network.

Diatomic Molecules Involving Dissimilar Atoms

Consider the compound hydrogen chloride (in the gaseous, liquid or solid state). This compound is not ionic (because the energy state on complete ionization would be higher. Instead, bonding between hydrogen and chlorine atoms is accomplished by the sharing of electrons in a molecular orbital, thus forming a single covalent bond (fig. 6).

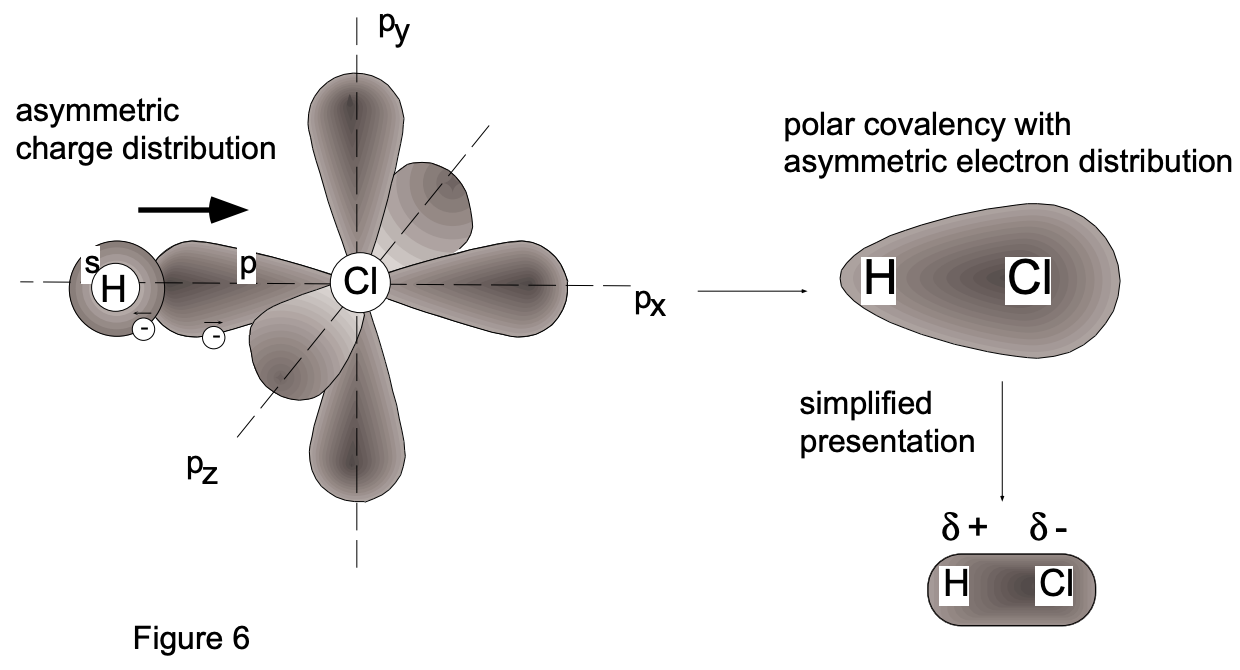
The electrons involved are the 1 s electron of the hydrogen atom and the unpaired \(3 p_{z}\) electron of the chlorine atom. After spin-pairing, a typical \(\sigma\) bond results in which each atom attains a noble gas structure: in \(\mathrm{HCl}\) the hydrogen atom is "involved" with two electrons, as in helium, and the chlorine atom with 18 electrons, as in argon. The other (inner) electrons of chlorine do not participate in the bonding; they are termed non-bonding.

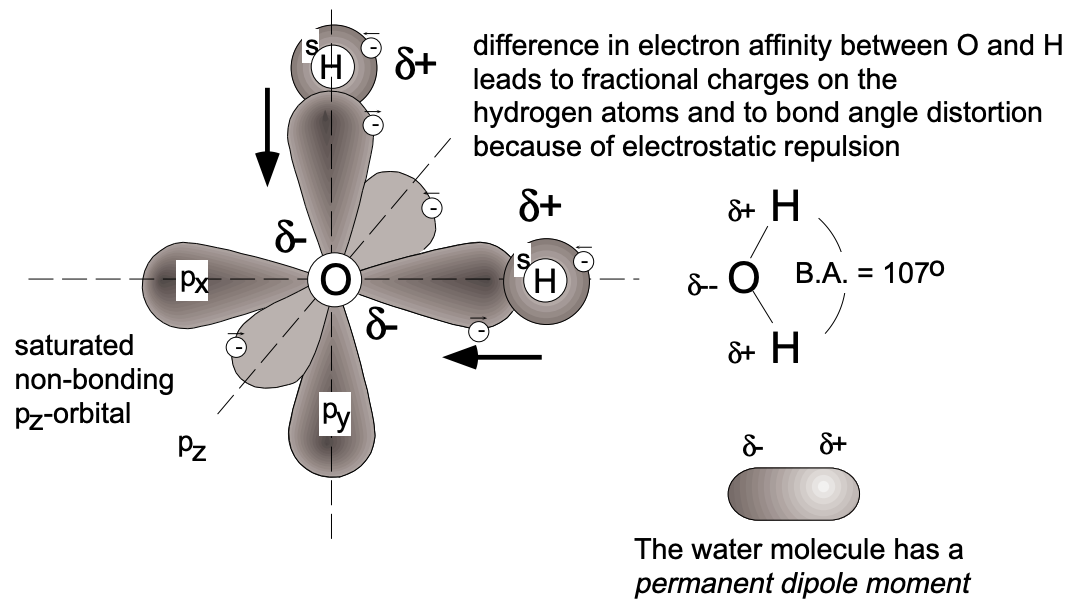
According to the above considerations, the bonding of \(\mathrm{HCl}\) may be taken as very similar to that of \(\mathrm{H}_{2}\). However, in the hydrogen molecule the electrons participating in the \(\sigma\) bond formation do not favor the proximity of either of the hydrogen nuclei - instead, they are equally shared. On the other hand, a preference for one nucleus (chlorine) is shown by the electrons of the \(\sigma\) bond in hydrogen chloride. This is because electrons, for energetic reasons, favor the environment of the more electronegative atom; in hydrogen chloride this is the chlorine atom and, consequently, the \(\sigma\) bond electrons spend more time in the vicinity of the chlorine atom. This situation results in the chlorine end of the molecule being fractionally negatively charged \(\left(\delta^{-}\right)\) and the hydrogen end being fractionally positively charged \(\left(\delta^{+}\right)\). We denote such an internal charge redistribution by the symbolism \(\mathrm{H}^{\delta+}-\mathrm{Cl}^{\delta-}\), where the \(\delta\) sign indicates a partial electronic charge; the bond is said to be polar. (The hydrogen molecule does not a priori exhibit such an "asymmetric charge distribution"; it may, however, acquire a temporary polarization.) Molecules with asymmetric electronic charge distribution have a permanent dipole moment, the value of which is given by the product of the fractional charge ( \(\delta^{+}\) must be equal to \(\delta^{-}\)) and the distance of charge separation \((\mathrm{L})\). Although dipole moments can be measured, their values do not allow us to directly calculate the polarity of bonds between atoms since the detailed internal charge distribution is unknown. The direction of electron drift and, to some extent, the magnitude of its effect can be estimated from the magnitude of the difference in electron affinity between the reaction partners. Because of a limited data base on electron affinity, L. Pauling introduced a related term, the relative electronegativity (see below). From the above considerations it should be clear that no sharp dividing line exists between ionic and covalent bonding. We might consider a completely ionic bond to result in cases where the electron drift is such that one atom (the cation) becomes entirely deficient in one or more electrons, and the other atom (the anion) becomes correspondingly electron-rich, the bonding electrons being entirely under the influence of the latter. Hydrogen halides are $\sigma$ bonded and have dipole moments; the bonds are referred to as polar covalency. The homonuclear diatomic molecules formed by the halogens, viz. \(\mathrm{F}_{2}, \mathrm{Cl}_{2}, \mathrm{Br}_{2}\) and \(\mathrm{I}_{2}\), are all \(\sigma\)-bonded systems involving spin-pairing of the various \(p_{z}\) electrons \(\left(2 p_{z}, 3 p_{z}\right.\), \(4 p_{z}\) and \(5 p_{z}\) respectively). They have no permanent dipole moments.

Energetics of Covalent Bonding

Pauling extensively treated the energetics of polar covalencies, encountered in all heteronuclear systems (such as \(\mathrm{H}-\mathrm{Cl}\) ) which have permanent dipole moments \(\left(\mathrm{H}^{\delta+}-\mathrm{Cl}^{\delta-}\right)\). His approach visualizes the bonding to consist of two components - a pure covalency and an ionic bonding component with attraction resulting from the interaction of the fractional charges on the nuclei involved.

Pauling determines the basic covalent bonding component, for example in the formation of \(\mathrm{HCl}\), from the experimentally obtained bond energies associated with the molecular species of the components, \(\mathrm{H}_{2}\) and \(\mathrm{Cl}_{2}\). For this purpose he made the basic assumption that the covalent bond component between the dissimilar atoms is given by the geometric mean of the pure covalent bond energies associated with these molecular species. Thus:

Pure Covalent Bond Energy of \(\mathrm{HCl}\):

\begin{aligned}
\mathrm{BE}_{\mathrm{HCl}} &=\sqrt{\mathrm{BE}_{\mathrm{H}_{2}} \times \mathrm{BE}_{\mathrm{Cl}_{2}}} \\
& \mathrm{H}_{2}: \mathrm{H}-\mathrm{H} \text { (Bond Energy }=\mathrm{BE}_{\mathrm{H}_{2}}=430 \mathrm{~kJ} / \mathrm{mole} \text { ) } \\
&\mathrm{Cl}_{2}: \mathrm{Cl}-\mathrm{Cl} \text { (Bond Energy }=\mathrm{BE}_{\mathrm{Cl}}=238 \mathrm{~kJ} / \mathrm{mole} \text { ) } \\
&\mathrm{BE}_{\mathrm{HCl}}=\sqrt{430 \times 238}=320 \mathrm{~kJ} / \text { mole }
\end{aligned}

The ionic contribution \((\Delta)\) to the polar covalent bonding is then obtained from the difference between the experimentally determined bond energy (for \(\mathrm{HCl}\), for example), which obviously must contain both components, and the calculated pure covalent bond energy:

\(\left.\Delta=\left[\mathrm{BE}_{\mathrm{HCl}} \text { (experimental }\right)\right]-\left[\mathrm{BE}_{\mathrm{HCl}} \text { (theoretical - covalent) }\right]\)

\(\text{(The experimentally determined} \mathrm{BE}_{\mathrm{HCl}}=426 \mathrm{~kJ} / \mathrm{mole}.)\)

\(\Delta=426-320=106 \mathrm{~kJ} / \text { mole }\)

In connection with the presently discussed work, Linus Pauling established the now generally used electronegativity scale, or, better, the scale of relative electronegativities. This scale, included in the Periodic Table of the Elements, is extremely helpful since values of the electron affinity are known thus far for only very few elements.

The electronegativity \((\mathrm{x})\) scale lists the relative tendency of the neutral elements to attract an additional electron. (The values of \(x\) are conventionally listed in electron Volts.) The scale listed was obtained by arbitrarily fixing the value of \(x_{H}=2.2\). Pauling obtained the values for the other elements by relating differences in electronegativity of reaction partners to the fractional ionic character (ionic bonding component) of the bond established between them:

\begin{aligned}
&\text { experimental } \mathrm{BE}_{\mathrm{AB}}=\sqrt{\mathrm{BE}_{\mathrm{AA}} \times \mathrm{BE}_{\mathrm{BB}}}+\mathrm{k}\left(\mathrm{x}_{\mathrm{A}}-\mathrm{x}_{\mathrm{B}}\right)^{2} \\
&\text { or } \\
&\Delta=96.3\left(\mathrm{x}_{\mathrm{A}}-\mathrm{x}_{\mathrm{B}}\right)^{2} \mathrm{~kJ}
\end{aligned}

According to Pauling, the bonding character between two different elements may be defined as:

ionic bonding for: \(\Delta x>1.7\); covalent bonding for: \(\Delta x<1.7\)

The fractional ionicity of polar covalent bonding as listed in the P/T is obtained by the relationship:

\(\%\) ionic bonding \(=\left(1-\mathrm{e}^{-0.25\left(\mathrm{x}_{\mathrm{A}}-\mathrm{x}_{\mathrm{B}}\right)^{2}}\right) \times 100\)

Bonding In Polyatomic Molecules

In the formation of covalent bonds between atoms in polyatomic molecules, the conditions that atomic orbitals distort so that maximum overlap may be achieved when bonding occurs produces more extensive changes of orbital geometry than is the case with diatomic molecules. It will be remembered that the changes which result in a \(\sigma\) bond formation in diatomic molecules are a distortion of the s orbitals or \(p\) lobes so that strongest bond formation results from the maximum overlap between the two joined nuclei. For polyatomic molecules extensive alterations in the spatial disposition of atomic orbitals do occur, and very often the unique orbital geometry of the original atomic orbitals is completely lost (fig. 7). It is sometimes convenient to view these alterations as occurring in each atom prior to bonding by a process involving the mixing, or hybridization, of atomic orbitals.

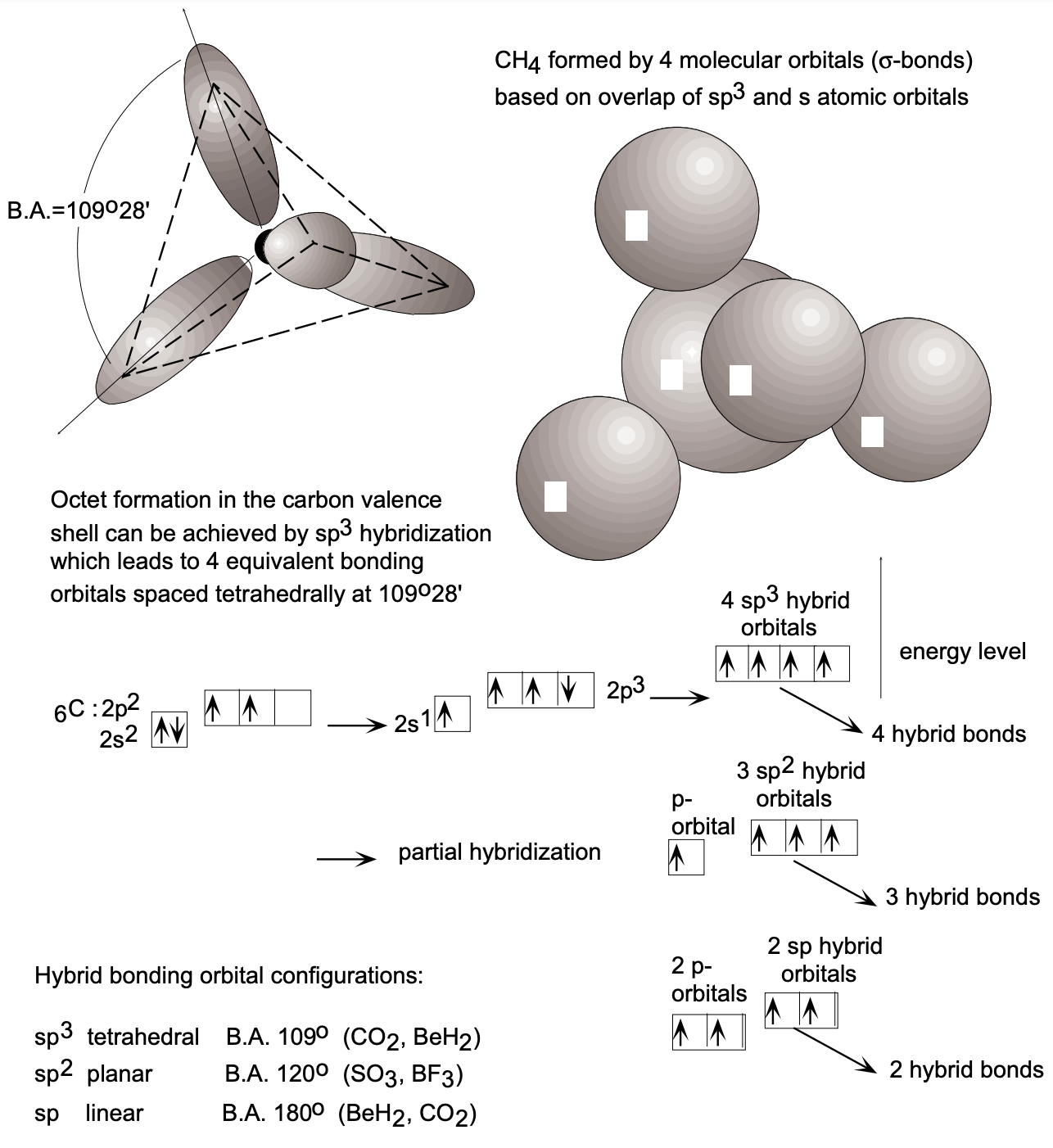
Bonding Involving Carbon

In methane \(\left(\mathrm{CH}_{4}\right)\) the four outer, or valence, electrons of carbon are shared with the electrons of hydrogen; there is spin-pairing (resulting in bond formation) between each individual hydrogen electron and one of the carbon valence electrons. The noble gas structure is thus attained by each nucleus: the carbon nucleus "sees" eight outer electrons and each \(\mathrm{H}\) nucleus "sees" two electrons. Consider now the orbitals which are involved in more detail. Each hydrogen has one spherical valence orbital (the 1s orbital) containing one electron, and covalent bond formation results from its distortion, overlap with the valence orbitals of carbon and spin-pairing.

According to the Aufbau principle and Hund's rule, in its ground state carbon has two electrons in the filled \(\mathrm{K}\) shell and four electrons in the \(\mathrm{L}\) shell: two 2 s electrons and two \(2 p\) electrons in singly occupied orbitals which are capable of covalent bond formation. This configuration provides, in principle, only two orbitals \(\left(2 p_{x}, 2 p_{y}\right)\) for covalent bond formation. However, with two covalencies carbon will not yield the desirable octet configuration. Such a configuration can be obtained if one of the two 2s electrons is "promoted" into the empty \(2 p_{z}\) orbital since this process results in four singly occupied orbitals - all of which, being singly occupied, are capable of bond formation. The dissimilar singly occupied orbitals can assume (and therefore will assume) upon bond formation a lower energy configuration involving a process called hybridization whereby the four orbitals (of two different types) hybridize into four identical orbitals of maximum equal spacing from each other (fig. 8). Thus the hybridized orbitals (\(sp^3\) hybrids) are lobes emanating from the carbon atom into the corners of a tetrahedron, forming bond angles of \(109^{\circ} 28^{\prime} . \mathrm{sp}^{3}\) hybridization is characteristic for carbon; however, other types of hybridization, \(\mathrm{sp}^{2}\) and \(\mathrm{sp}\), are encountered in other elements as well. Boron, for example, will tend to promote one of its two 2s electrons into a \(2 p\) state and, by hybridization, form three equivalent \(s p^{3}\) orbitals which assume planar orientation with band angles of \(120^{\circ}\). Beryllium forms sp hybrid orbitals of linear orientation (the bond angle is \(\left.180^{\circ}\right)\). All hybrid orbitals are capable of \(\sigma\) bond formation.

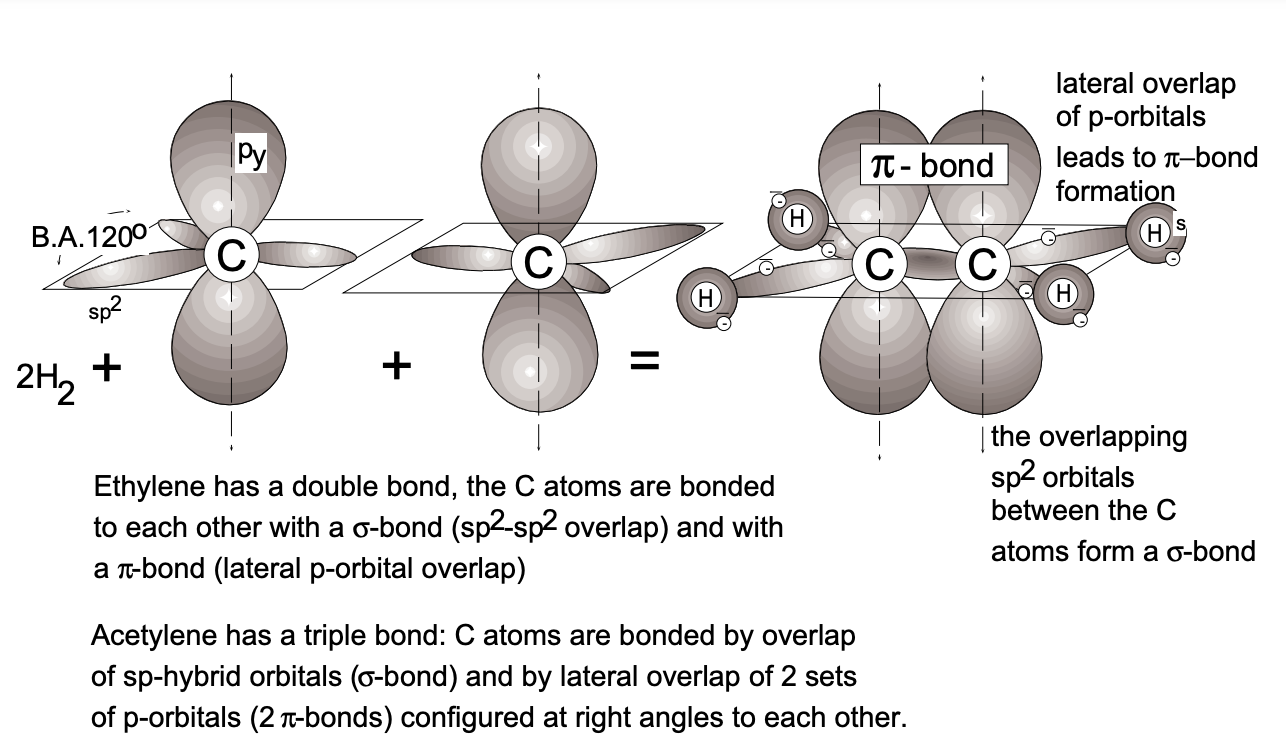
The great diversity of carbon compounds (it forms more compounds than all the rest of the elements in the Periodic Table) can be attributed to the hybridization capability of the carbon orbitals \(\left(\mathrm{sp}^{3}, \mathrm{sp}^{2}\right.\) and \(\left.\mathrm{sp}\right)\). As a consequence, carbon forms not only axisymmetric \(\sigma\) bonds (through axial orbital overlap), but also \(\pi\) bonds (through lateral orbital overlap). In the compound ethane \(\left(\mathrm{H}_{2} \mathrm{C}=\mathrm{CH}_{2}\right)\), the interactive carbon atoms undergo \(\mathrm{sp}^{2}\) hybridization for a \(\sigma\) bond by overlap of two \(\mathrm{sp}^{2}\) hybrid orbitals and form, in addition, a \(\pi\) bond by lateral overlap of the remaining non-hybridized \(p\) orbitals. (Double bonds involve one \(\sigma\) and one \(\pi\) bond.) In acetylene \((\mathrm{HC} \equiv \mathrm{CH})\), we find sp hybridization and, by axial overlap, \(\sigma\) bond formation as well as lateral overlap of the remaining non-hybridized \(p_{x}\) and \(p_{y}\) orbitals which form two \(\pi\) bonds (fig. 9).

Figure 9 Double and Triple Bonds

METALLIC BONDING

The stability of both covalent and metallic bonds may be regarded as arising from the potential energy lowering experienced by valence electrons under the influence of more than one nucleus. In metals, where the valence electrons are not as tightly bound to their ion cores, we cannot expect the formation of strong electron-pair bonds. The bond energies of known diatomic molecules of metallic elements are, in fact, smaller than those consisting of nonmetallic elements: \(104 \mathrm{~kJ} /\) mole for \(\mathrm{Hg}_{2}\). Only diatomic molecules of the semi-metals have relatively high binding energies \(\left(385 \mathrm{~kJ} / \mathrm{mole}\right.\) for \(\mathrm{As}_{2}\), \(293 \mathrm{~kJ} / \mathrm{mole}\) for \(\mathrm{Sb}_{2}\) and \(163 \mathrm{~kJ} /\) mole for \(\mathrm{Bi}_{2}\) ). These values reflect multiple bonding. Much greater stability is possible in larger aggregates of atoms such as bulk metals.

The known properties of metals, such as low electrical resistance and malleability, support the conceptual view that the valence electrons in metals never remain near any
particular atom very long, but drift in a random manner through the lattice of ion cores. We may therefore visualize metals as a lattice of ion cores being held together by a gas of free electrons.

(Bonding in metallic systems is discussed in more detail in LN-3.)

SECONDARY (van der WAALS) BONDING

Primary bonding (ionic, covalent and metallic) is strong and the energies involved range from about 100 to 1000 kJ/mole. In contrast, secondary bonding is weak, involving energies ranging from about 0.1 to 10 kJ/mole. While this type of bonding, also referred to as “residual”, is weak, it is essential in the functioning of our environment. Coke would likely be gaseous and not a bubbly, refreshing brew were it not for secondary bonding, nor would catalytic converters function.

The energy difference between the liquid and vapor states of a given system is given by the heat of vaporization, i.e. the heat required to convert a given liquid into a vapor (normally) at the boiling point temperature at 1 atm pressure. The energy difference is due to intermolecular attraction between molecules at close distance of separation. This phenomenon of attraction through secondary bonding can best be considered between a single pair of molecules, but recognizing that the forces are of longer range. Four types of intermolecular forces can be identified.

1. Dipole-Dipole Interaction: Molecules with permanent dipoles (such as water, alcohol and other organic compounds with functional groups) exert a net attractive force on each other as a result of varying degrees of alignment of oppositely charged portions of the molecules (fig. 10). For two polar molecules with a dipole moment of \((\mu)\) separated by a distance of (r), the energy of attraction can be quantified as:

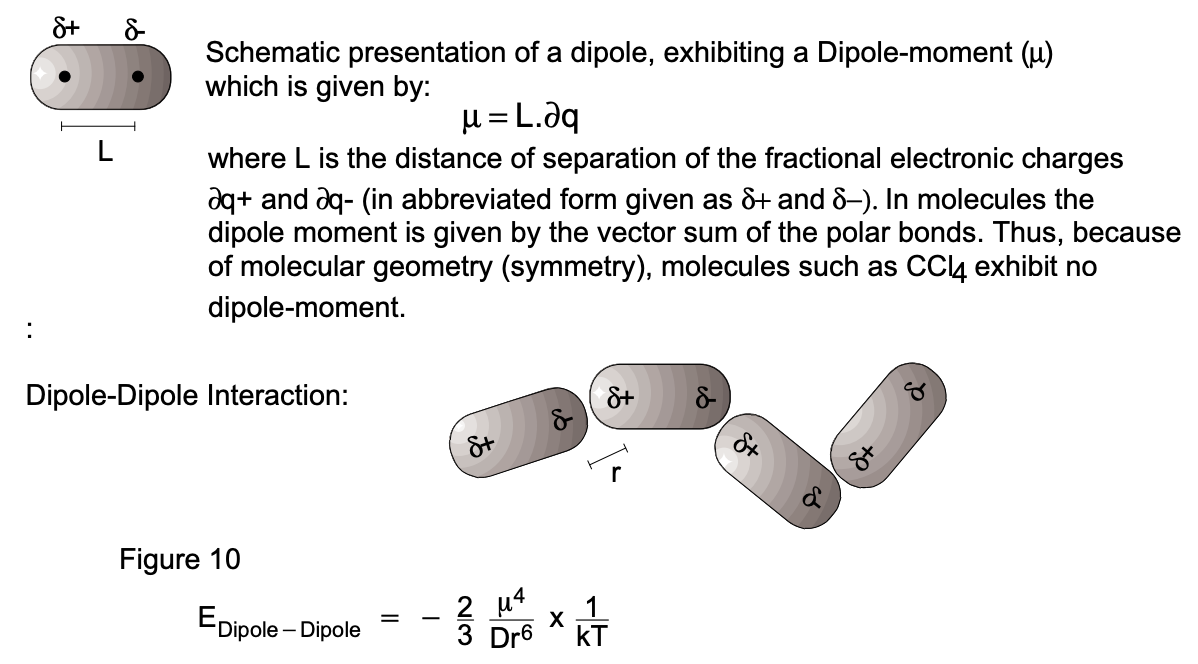
where \(\mu\) is the dipole moment, \(r\) is the distance of approach of the oppositely charged molecular portions, \(k\) is the Boltzmann constant (see \(P / T)\) and \(T\) is the absolute temperature in \(\mathrm{K}\).

The molar energies of attraction associated with dipole-dipole interaction range from 0 to about \(10 \mathrm{~kJ} /\) mole. These forces are primarily responsible for the liquid state (at room temperature) of most polar organic molecules; they are a contributing factor for \(\mathrm{H}_{2} \mathrm{O}\) to be liquid at room temperature, and are responsible for alcohol being a liquid.

2. Dipole-Induced Dipole Interaction: A dipole in one molecule can interact with and polarize the electrons of a neighboring non-polar molecule, thus generating an induced dipole which will experience an attractive force with the polarizing, polar dipole (fig. 11). P. Debye showed that in a molecule with a "polarizability" of \((\alpha)\) the attractive potential arising from dipole-induced dipole interaction is given as:

\(\mathrm{E}_{\text {Dipole-Induceddipole }}=-\dfrac{2 \alpha \mu^{2}}{\mathrm{Dr}^{6}}\)

Induced dipole interaction is important in aqueous solutions and very effective during adsorption of inert molecules on active solid substrates.

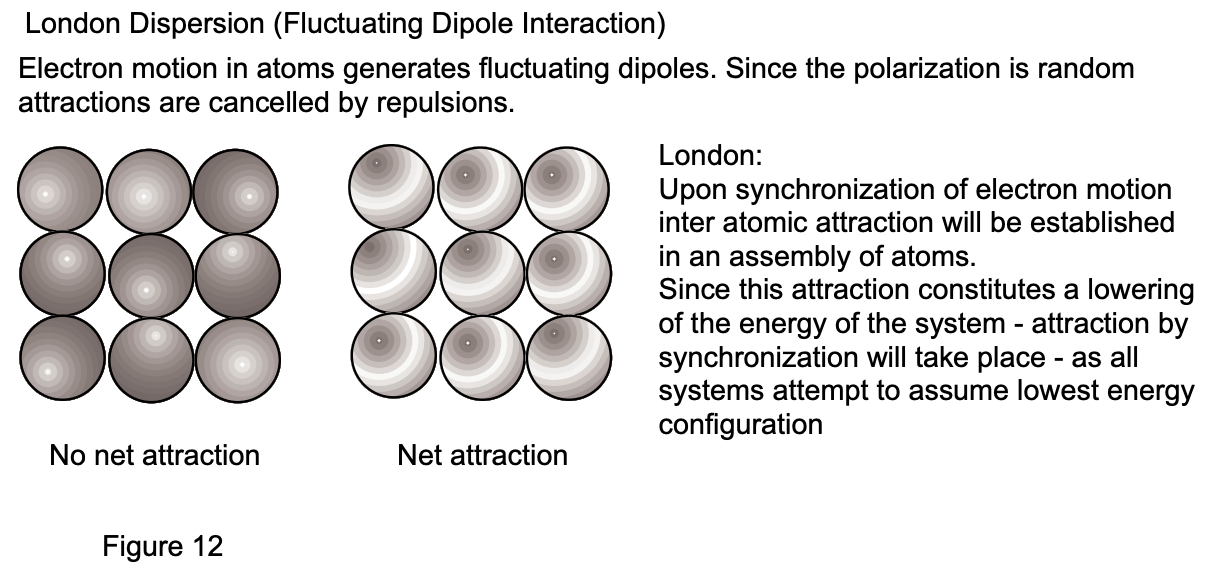
3. London Dispersion Forces: It is a well-known fact that all substances, including rare gases and hydrogen, assume liquid state at finite temperature, an indication of the existence of attractive interatomic and intermolecular forces, even in the absence of permanent dipole systems. The origin of this force has been proposed by F. London in 1930. Accordingly, orbiting electrons will at any instance generate a "temporary dipole", the configuration of which changes as the electrons move. Since all atoms of a given system similarly experience temporary instantaneous dipole moments, their effect is expected to be cancelled because of the statistically random orientation of dipoles. It is evident that, should the dipoles be synchronized in a given assembly of atoms, then a net attractive force would result (fig. 12). But since such an attractive force constitutes a lowering of the energy of a given system, synchronization can and will take place because all systems will attempt to assume minimum energy configuration. The London dispersion force can be formulated as:

\(\mathrm{E}_{\text {London }}=-\mathrm{K} \dfrac{\alpha^{2}}{\mathrm{r}^{6}}\)

The attractive London forces are small, as manifested by the very low boiling points of the smaller rare gases, of hydrogen and nitrogen.

4. Hydrogen Bonding: The short and long range dipole interactions calculated from molecular dipole moments are inadequate in explaining a multitude of phenomena in organic as well as some inorganic systems. L. Pauling studied such

phenomena and concluded the existence of highly specific attractive interaction between hydrogen that is acidic (carries a fractional positive charge) and the elements O, F, N and, to a lesser extent, S in both organic and inorganic molecules. This interaction, which can as yet not be formulated, is referred to as hydrogen bonding; its magnitude, ranging up to 40 kJ/mole, is significantly larger than that of any other secondary bonding type. Hydrogen bonding is considered instrumental in controlling most properties of water, is a key element in the structure of nucleic acid and thought to be an essential component in memory functions of the human brain.