Discovery of Quantization

Skills to Develop

• Explain the significance of spectroscopy, wave-particle duality
• Describe the contributions of Bohr and Planck to "old quantum mechanics"

The history of quantum mechanics is often divided into 2 parts: the "Old Quantum Mechanics" and the "New Quantum Mechanics." Before either quantum mechanics, physicists described the world using "Classical Mechanics," which is like what you've probably studied before in physics class: Newtonian mechanics (forces, accelerations, etc), electricity and magnetism using Maxwell's equations. . . all these approaches work well for big things that aren't moving too fast. There are two qualities of classical mechanics that quantum mechanics altered. First, in classical mechanics energy and velocity and such quantities can have any value. If you drop a ball, it accelerates smoothly from 0 to a final velocity, rather than moving jerkily from step to step. The "Old Quantum Mechanics" got rid of the assumptions that energy and velocity should be "continuous." The other aspect of classical mechanics was the idea of a trajectory: the path taken by a moving object. If you launch a missile or a space shuttle, you can calculate almost exactly the path it will follow; if you have perfect knowledge of the forces acting on it, you can calculate its path perfectly. The "New Quantum Mechanics" which is described more in the later section on orbitals essentially said that there is no trajectory for small particles, so you can only describe them using statistics, not actually know where they are or what path they follow.

Spectroscopy

The discovery of spectroscopy in 1859 presented a problem for chemists. Spectroscopy essentially means looking at the wavelengths of light that are absorbed or emitted from a sample. Any time you look at colors, you are doing a sort of spectroscopy, because color comes from particular wavelengths of light. Paint absorbs certain wavelengths, so what we see is the color of the other wavelengths. Computer screens can emit certain wavelengths of light so we see the colors that correspond to those wavelengths. But you can look more carefully, by splitting light into its component wavelengths, using a prism or a diffraction grating. If you do this with sunlight, as Newton did, you see a rainbow. If you do this with the light emitted by a very hot sample of an element, you will see just a few separate lines: the sample emits only specific wavelengths, instead of a smooth rainbow with a little of each. But chemists had trouble explaining why only these particular wavelengths were emitted. The wavelengths are called lines, and the collection of lines is the spectrum.

Examples of an element's spectrum

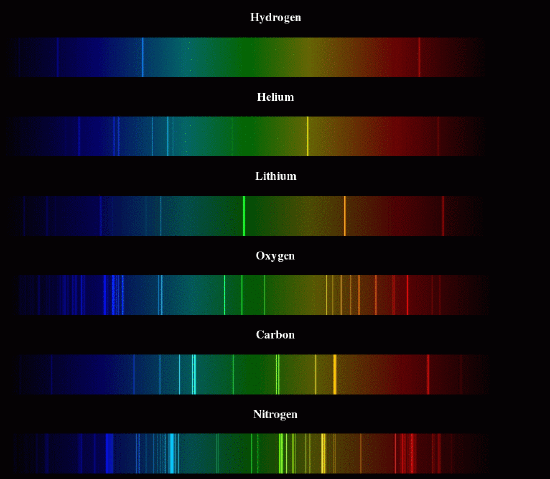
In 1885 (25 years after the introduction of the spectrometer), Balmer, a teacher, studied the 4 lines emitted by very hot hydrogen atoms, and noticed a pattern. The wavelengths could be calculated from

\[\lambda = C\frac{n^{2}}{n^{2}-2^{2}}\]

where C is a constant and n is a whole number (3, 4, 5, or 6 for the 4 known lines). He suggested that there might be other lines corresponding to replacing the 2² in his formula with 3², 4², etc. Rydberg later rewrote Balmer's formula as follows, using the wavenumber (1/λ) which is still commonly used in labs today with the unit cm⁻¹

\[\frac{1}{\lambda}=R \left(\dfrac{1}{n_{f}^{2}}-\dfrac{1}{n_{i}^{2}}\right)\]

where R is called the Rydberg constant, and n_f and n_i are integers, and n_i is larger than n_f. Until 1908, the only known lines had n_f = 2, but then finally lines given by n_f = 3 were found, and later lines with n_f = 4, 5 were found also, proving Balmer correct.

The "Old Quantum Mechanics"

This is a good time to review the previous section Discovery of Sub-Atomic Particles. Recall the use of gas discharge tubes in discovering X-rays. This started a long debate about whether X-rays were waves (like light) or particles, like electrons. They couldn't be charged particles, because they weren't affected by magnets, but they didn't seem to reflect or diffract either. (Diffract means waves changing direction after passing through a gap about the size of the wavelength.) Eventually Stokes realized that X-rays were light with a very short wavelength, so it wouldn't diffract without very tiny gaps. Von Laue proposed that salt crystals could be used to diffract X-rays, because the gaps between ions in crystals are very small. This is the basis of X-ray diffraction, which is now used commonly to find structures of molecules. Also, remember the young chemist Moseley who figured out the fundamental order of the periodic table? He was essentially doing X-ray spectroscopy, using an electron beam to make elemental samples emit X-rays. He measured the wavelengths of these X-rays using diffraction by salt crystals. Like Balmer, he found a fascinating pattern in his line spectra.

Review as well Rutherford's nuclear model of the atom in the same section, proposed in 1911 (around the time that Balmer's hypothesis was proved correct). After various proposals, his experiments showed clearly that there was a dense, central part of the atom with most of the weight and the positive charge, which is called the nucleus. Around the nucleus, electrons move, occupying a much larger volume than the nucleus. But the physicists had some problems with this model. If the electrons weren't moving, they should "fall" into the nucleus. If they were moving around the nucleus, when they changed direction (to stay near the nucleus) they should emit light. The oscillating charged particles would be like a miniature cell phone tower, emitting radiation at high frequency. Emitting light would cause them to lose kinetic energy, and very quickly they should fall into the nucleus. To solve this problem, Bohr employed quantum theory, which had been introduced by Planck in 1900.

Planck used quantum theory to explain blackbody or thermal radiation. Recall the problem with Rutherford's model, that acceleration (including direction change) of charged particles produces light (not necessarily visible light, but electromagnetic radiation of some wavelength). The atoms and ions in normal objects are always moving a little, and the hotter they are, the more they move. These movements mean that they bump into each other and change direction; these collisions result in emission of radiation if charged particles are involved. The light emitted by normal objects at normal temperatures is usually IR or lower energy (animals emit IR thermal radiation, which is how night-vision goggles work); incandescent (normal old-fashioned) light bulbs emit visible light and IR because the filament is much hotter than room temperature. In English, we talk about "red-hot" or "white-hot" to describe temperatures: glass or metal that is being shaped is often red-hot, hot enough to emit red light. White-hot is even hotter, hot enough to emit white light (all the colors). But it was very hard to explain the spectrum of thermal radiation produced by objects at different temperatures (what wavelengths of light were produced and how much of each). Planck had to introduce quantization to get a good model. He proposed that light isn't just a wave, but it comes small separate packages, called quanta. The energy of a quantum of light is 

\[E=h u \]

where h is Planck's constant (6.626 x 10^-34 Js) and ν (Greek letter read as "nu") is the frequency of the light in Hz. Most scientists didn't like this idea (it seemed very strange!) but it worked.

Wave-Particle Duality

The Wave-Particle Duality means that something can behave like a wave and also behave like a particle. This was first applied to light. Before quantization was proposed, physicists knew that light behaves as a wave (as described in the previous section. When Planck proposed quantization, he thought it was a property of atoms, not light. However, Einstein applied Planck's theory to explain the photoelectric effect, and clearly showed that light is a particle. The photoelectric effect means that when light (such as UV light) shines on a metal surface, sometimes it knocks electrons off the surface, creating a "photocurrent". It turns out that photocurrent is only produced when light has a sufficient frequency, and that increased intensity of light only produces more photocurrent, not photoelectrons with higher kinetic energy. And higher frequencies of light produce photoelectrons with more kinetic energy, but not more electrons. Einstein explained this by saying that light comes in particles with energy proportional to frequency (E = hν, which is the same formula Planck used in which ν is the frequency and h is a constant). To create a photoelectron, the light particle or photon must have more energy than the energy holding the electron on the surface. Any extra energy in the photon turns into kinetic energy for the electron.

Bohr's Model

Bohr used Planck's quantum concept to try to explain the Rutherford model of the atom. He focused on the hydrogen atom, with just one electron around the nucleus. Surprisingly, it was dimensional analysis that lead him to Planck's theory. He liked the "solar system" model, in which electrons orbit the nucleus like planets orbit the sun. He realized that an orbit would have a characteristic radius (distance between nucleus and electron) and also that h²/m•e² would have units of length (check this yourself, but note that you'll need to include another quantity, the permitivity of free space). So he used classical physics, including Coulomb's law and 

\[a = \frac{v^{2}}{r}\]

to look for an equation for stable orbits (he just assumed that in a stable orbit, the acceleration wouldn't cause radiation). He got part of the way (calculating the total energy of the orbits including kinetic and potential energy), then got stuck. Luckily, a spectroscopist then introduced him to Balmer's formula. When he saw that, the answer suddenly became clear to him. He assumed that the lines in the spectrum come from electrons moving from one stable orbit to another, and the wavelength of the light emitted equals the energy difference of the orbits. He amazed everyone by deriving the Rydberg constant (which was experimentally known to be 109677 cm⁻¹) in terms of fundamental constants: 

\[R=\frac{e^{4}m}{8\epsilon_{0}^{2}h^{3}c}\]

and it worked out correct! (Check for yourself; ε₀ is again the permitivity of free space.) So Bohr's model worked well for explaining the hydrogen spectra: in stable orbits, which had only certain allowed energies, there was no radiation; light (a single photon) was absorbed or emitted when changing orbits, and its wavelength matched the energy difference of the orbits. This theory also worked to explain some lines in the sun's spectrum, which came from He⁺; to calculate these you have to use the atomic number Z to account for the larger charge in the nucleus. It turned out that his formula works for all single-electron atoms.

Essentially, his model predicted stable orbits with energies determined by a quantum number, corresponding to the integers in Rydberg's formula. Orbits with one value of the quantum number are called a shell. He also figured out that orbits didn't have to be circles, and didn't have to all be in the same flat plane. He added 2 more quantum numbers to indicate the shape (circle or ellipse) and the orientation of the orbits.

However, his theory didn't work for multi-electron atoms very well. Bohr worked on extending it for more electrons, and he found that this was easiest for alkali atoms. Bohr found that he could do ok by treating the alkali atoms as having only one electron, and including all the other electrons as part of a bigger "nucleus" with a +1 charge. Bohr used spectroscopic data to arrange the elements in roughly the same pattern as a modern periodic table, with periods of 2, 8, 8, 18, 18, and 32 elements, and some divisions between the electrons in each period, that he did not get exactly right. Each row consisted of filling one shell. Recall that early periodic tables didn't have the modern shape; it was at this time that the modern shape started to emerge. Other chemists we'll study later (Lewis and Langmuir) were arranging the elements by chemical properties, with similar results. The mathematical basis of this pattern didn't become clear until the "new quantum mechanics" was introduced.

Contributors and Attributions

• Emily V Eames (City College of San Francisco)