Electron Configurations

Skills to Develop

• Predict and illustrate electron configurations

The wavefunctions in the previous section were derived for single-electron atoms only. It's really hard if not totally impossible to solve the Schrodinger equation perfectly when there are 2 or more electrons, because of electron-electron repulsions which make the Hamiltonian incredibly complicated. However, it turns out that we can approximate the orbitals in other atoms with small modifications of the hydrogen wavefunctions, like decreasing the nuclear charge to account for electron repulsion.

Electron Configurations

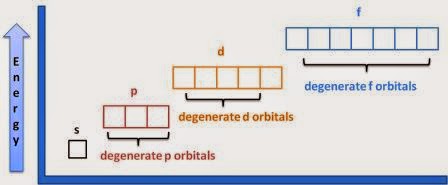
Bohr figured out the number of electrons in each shell, where a shell is all the electrons with the same principal quantum number. The pattern he used, which you can verify with the periodic table, was 2, 8, 8, 18, 18, 32, 32. However, he was not as clear about the arrangement into subshells, which are groups of electrons with the same principle and angular momentum quantum numbers, such as 1s or 2p. This became much clearer after Schrodinger's wavefunctions for the hydrogen atom were introduced, because the solution wavefunctions clearly had only certain allowable ℓ values and m_ℓ values. Although all the orbitals in a shell have the same energy in a single electron atom, when there are more electrons the subshells have different energies. This is because the larger ℓ is within a shell, the farther the electron usually is from the nucleus. In s orbitals, the electrons are often close to the nucleus, so other electrons don't block the nuclear charge much. In d and f orbitals, the electrons are far from the nucleus and do get blocked. Thus, orbitals tend to fill in the order of lowest n and lowest ℓ first.

Orbitals with the same energy are called degenerate. (In other contexts, degenerate means immoral, or other bad things.) In general, the more complications you add, like more electrons, neighboring atoms, magnetic fields, etc, the fewer orbitals are degenerate. So for a hydrogen atom by itself, all the orbitals in each shell are degenerate. When you move to a lonely helium atom, the orbitals in the subshells are degenerate. When you make chemical bonds, the orbitals in subshells are no longer degenerate. When you apply a magnetic field, the electrons in the same orbital are not degenerate.

A simple diagram showing degenerate orbitals.

Simple Rules for Predicting Electron Configurations of Atoms

How to predict electron configurations for elements? Electron configuration just means how many electrons in each orbital. You will need to know the number of electrons you are using. You can get this from the periodic table (the atomic number − charge if it's an ion). Or you might just be given the atomic number. If you have a periodic table, it's easy, because of the shape of the table. If you go to the periodic table on this site, you'll see it has a blue block, a red block, a yellow block and a green block. The code is blue = s; yellow = p; red = d; and green = f. The alkali metals and alkaline earth metals have their highest energy electrons in an s orbital. The highest energy electrons, the ones in the highest shell, are called valence electrons. The main group (yellow) including halogens and noble gases, have their highest electrons in p orbitals. The transition metals have theirs in d orbitals, and the lanthanoides and actinoids in f orbitals. Notice that each section is 2, 6, 10 or 14 elements across, because there are 1,3,5,7 orbitals in the s, p, d, and f subshells, and each orbital holds 2 electrons. So you can write the electron configuration just by looking at the periodic table. Follow your way along, writing how many electrons are in each subshell, until you have the right number of electrons total. For instance, for Al, you would have 1s²2s²2p⁶3s²3p¹. Notice that we indicate the number of electrons in each subshell using superscripts we we write electron configurations.

Another trick you can use to write electron configurations is to follow the arrows on this diagram. The filling pattern is named "aufbau" which means "building up" in German, or so I've heard. Notice that you don't actually fill all the subshells in one shell before moving on to the next. This can be a little confusing (espcially because the s orbitals are only slightly lower than the previous d orbitals, and in ions the energy order switches back!). Either use this diagram or a periodic table, and you'll get the right answers as long as you are careful to count from the top of the periodic table. Notice how the first row of d comes after the 4th row of s? But we can have 3d orbitals, so the first row of d is 3d, not 4d.

Often we don't want to write out all the electrons for a heavy atoms, because the inner ones are just the same as all the other elements. So we might show only the valence electrons, which means in this case the ones added on this row of the periodic table, or after the last noble gas. So we might write Ti as [Ar]4s²3d², which just means that it has the same configuration as argon, + 4s²3d².

The next question comes when not all the orbitals in a subshell are filled. Do you pair electrons or put them in separate orbitals? For instance, consider carbon. You can represent its electron configuration like this, with the arrows up and down representing the electron spin.

But which of the 3 possibilities is it? Remember that electron spin showed up in spectroscopy with magnetic fields. The electrons are like tiny magnets, and when they are paired (one up, one down) they cancel each other out and don't seem magnetic unless you look really hard. But you know that there are lots of very magnetic materials out there (maybe you use them on your fridge; you also use them in headphones and other devices). The reason they are magnetic is because the bottom arrangment is the lowest energy. Electrons prefer to have the same spin in different orbitals, where they repel each other less (among other more complicated reasons). This is called Hund's Rule. The reason the best magnets are transition metals or lanthanoides is that d and f orbitals have space to spread out 5 or 7 electrons with the same spin.

The only other thing you need to know about electron configurations right now is that there are some exceptions to the rules about what order they fill in (mostly in the d and f blocks). These aren't very important. The other thing you might want to know is whether the electron configuration in isolated atoms is important to chemists. Mostly only the valence electrons are affected by bonding, so the elemental configuration will probably still apply to the core electrons. And the atomic electron configurations match the reactivity patterns that the periodic table was originally based on, so that's useful. The other reason is that these rules apply almost the same to real chemical situations. Even if the orbitals are more complicated molecular orbitals (we'll study these later) instead of atomic orbitals, you still fill them from lowest to highest and use Hund's rule.

Outside Links

• CrashCourse Chemistry: The Electron (13 min)
• Khan Academy: Electron Configurations 2 (10 min)

Contributors and Attributions

• Emily V Eames (City College of San Francisco)