12.E: Kinetics (Exercises)
- Last updated
- Save as PDF
- Page ID
- 46044
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)12.1: Chemical Reaction Rates
Q12.1.1
What is the difference between average rate, initial rate, and instantaneous rate?
- Solution
-
First, a general reaction rate must be defined to know what any variation of a rate is. The reaction rate is defined as the measure of the change in concentration of the reactants or products per unit time. The rate of a chemical reaction is not a constant and rather changes continuously, and can be influenced by temperature. Rate of a reaction can be defined as the disappearance of any reactant or appearance of any product. Thus, an average rate is the average reaction rate over a given period of time in the reaction, the instantaneous rate is the reaction rate at a specific given moment during the reaction, and the initial rate is the instantaneous rate at the very start of the reaction (when the product begins to form).
The instantaneous rate of a reaction can be denoted as \[ \lim_{\Delta t \rightarrow 0} \dfrac{\Delta [concentration]}{\Delta t} \nonumber \]
Q12.1.2
Ozone decomposes to oxygen according to the equation \(\ce{2O3}(g)⟶\ce{3O2}(g)\). Write the equation that relates the rate expressions for this reaction in terms of the disappearance of O3 and the formation of oxygen.
- Solution
-
For the general reaction, aA ---> bB, the rate of the reaction can be expressed in terms of the disappearance of A or the appearance of B over a certain time period as follows.
\[- \dfrac{1}{a}\dfrac{\Delta [A]}{\Delta t} = - \dfrac{1}{b}\dfrac{\Delta [B]}{\Delta t} = \dfrac{1}{c}\dfrac{\Delta [C]}{\Delta t} = \dfrac{1}{d}\dfrac{\Delta [D]}{\Delta t}\]
We want the rate of a reaction to be positive, but the change in the concentration of a reactant, A, will be negative because it is being used up to be transformed into product, B. Therefore, when expressing the rate of the reaction in terms of the change in the concentration of A, it is important to add a negative sign in front to ensure the overall rate positive.
Lastly, the rate must be normalized according to the stoichiometry of the reaction. In the decomposition of ozone to oxygen, two moles of ozone form three moles of oxygen gas. This means that the increase in oxygen gas will be 1.5 times as great as the decrease in ozone. Because the rate of the reaction should be able to describe both species, we divide the change in concentration by its stoichiometric coefficient in the balanced reaction equation to deal with this issue.
Therefore, the rate of the reaction of the decomposition of ozone into oxygen gas can be described as follows:
\[Rate=-\frac{Δ[O3]}{2ΔT}=\frac{Δ[O2]}{3ΔT}\]
- Answer
-
$$Rate=-\frac{Δ[O3]}{2ΔT}=\frac{Δ[O2]}{3ΔT}\]
Q12.1.3
In the nuclear industry, chlorine trifluoride is used to prepare uranium hexafluoride, a volatile compound of uranium used in the separation of uranium isotopes. Chlorine trifluoride is prepared by the reaction \(\ce{Cl2}(g)+\ce{3F2}(g)⟶\ce{2ClF3}(g)\). Write the equation that relates the rate expressions for this reaction in terms of the disappearance of Cl2 and F2 and the formation of ClF3.
- Solution
-
In this problem we are asked to write the equation that relates rate expressions in terms of disappearance of the reactants of the equation and in terms of the formation of the product. A reaction rate gives insight to how rate is affected as a function of concentration of the substances in the equation. Rates can often be expressed on graphs of concentration vs time expressed in change (\({\Delta}\)) of concentration and time and in a short enough time interval, the instantaneous rate can be approximated. If we were to analyze the reaction given, the graph would demonstrate that Cl2 decreases, that F2 decreases 3 times as quickly, and then ClF3 increases at a rate doubles. The reactants are being used and converted to product so they decrease while products increase.
For this problem, we can apply the general formula of a rate to the specific aspects of a problem where the general form follows: \[aA+bB⟶cC+dD\nonumber \].
And the rate can then be written as \(rate=-\frac {1}{a}\frac{{\Delta}[A]}{{\Delta}t}\) \(=-\frac {1}{b}\frac{{\Delta}[B]}{{\Delta}t}\) \(=\frac {1}{c}\frac{{\Delta}[C]}{{\Delta}t}\) \(=\frac {1}{d}\frac{{\Delta}[D]}{{\Delta}t}.\) Here the negative signs are used to keep the convention of expressing rates as positive numbers.
In this specific case we use the stoichiometry to get the specific rates of disappearance and formation (back to what was said in the first paragraph). So, the problem just involves referring the to the equation and its balanced coefficients. Based upon the equation we see that Cl2 is a reactant and has no coefficient, F2 has a coefficient of 3 and is also used up, and then ClF3 is a product that increases two-fold with a coefficient of 2. So, the rate here can be written as: \[rate=-\frac{{\Delta}[Cl_2]}{{\Delta}t}=-\frac {1}{3}\frac{{\Delta}[F_2]}{{\Delta}t}=\frac {1}{2}\frac{{\Delta}[ClF_3]}{{\Delta}t}\nonumber \]
- Answer
-
\[\ce{rate}=+\dfrac{1}{2}\dfrac{Δ[\ce{CIF3}]}{Δt}=−\dfrac{Δ[\ce{Cl2}]}{Δt}=−\dfrac{1}{3}\dfrac{Δ[\ce{F2}]}{Δt}\nonumber \]
Q12.1.4
A study of the rate of dimerization of C4H6 gave the data shown in the table:
\[\ce{2C4H6⟶C8H12}\nonumber \]
| Time (s) | 0 | 1600 | 3200 | 4800 | 6200 |
|---|---|---|---|---|---|
| [C4H6] (M) | 1.00 × 10−2 | 5.04 × 10−3 | 3.37 × 10−3 | 2.53 × 10−3 | 2.08 × 10−3 |
- Determine the average rate of dimerization between 0 s and 1600 s, and between 1600 s and 3200 s.
- Estimate the instantaneous rate of dimerization at 3200 s from a graph of time versus [C4H6]. What are the units of this rate?
- Determine the average rate of formation of C8H12 at 1600 s and the instantaneous rate of formation at 3200 s from the rates found in parts (a) and (b).
- Solution
-
1.) The average rate of dimerization is the change in concentration of a reactant per unit time. In this case it would be:
\(rate\) \(of\) \(dimerization=-\frac{\Delta [C_4H_6]}{\Delta t}\)
Rate of dimerization between 0 s and 1600 s:
\(rate\) \(of\) \(dimerization=-\frac{5.04×10^{-3}M-1.00×10^{-2}M}{1600 s-0 s}\)
\(rate\) \(of\) \(dimerization=3.10 × 10^{-6} \frac{M}{s}\)
Rate of dimerization between 1600 s and 3200 s:
\(rate\) \(of\) \(dimerization=-\frac{3.37×10^{-3}M-5.04×10^{-3}M}{3200 s-1600 s}\)
\(rate\) \(of\) \(dimerization=1.04 × 10^{-6} \frac{M}{s}\)
2.) The instantaneous rate of dimerization at 3200 s can be found by graphing time versus [C4H6].
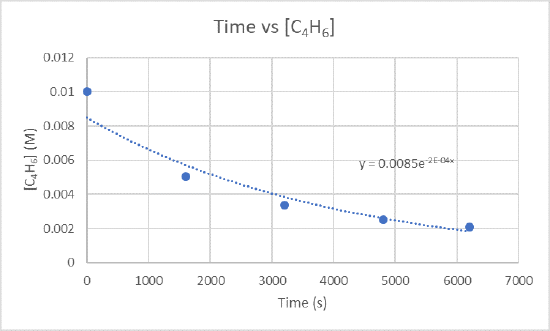
Because you want to find the rate of dimerization at 3200 s, you need to find the slope between 1600 s and 3200 s and also 3200 s and 4800 s.
For the slope between 1600 s and 3200 s use the points (1600 s, 5.04 x 10-3 M) and (3200 s, 3.37 x 10-3 M)
\(\frac{3.37×10^{-3}M-5.04×10^{-3}M}{3200 s-1600 s}\)
\(\frac{-0.00167 M}{1600 s}\)
\(-1.04×10^{-6}\frac{M}{s}\)
For the slope between 3200 s and 4800 s use the points (3200s, 3.37 x 10-3 M) and (4800s, 2.53 x 10-3 M)
\(\frac{2.53×10^{-3}M-3.37×10^{-3}M}{4800 s-3200 s}\)
\(\frac{-8.4×10^{-4} M}{1600 s}\)
\(-5.25×10^{-7}\frac{M}{s}\)
Take the two slopes you just found and find the average of them to get the instantaneous rate of dimerization.
\(\frac{-1.04×10^{-6}\frac{M}{s}+-5.25×x10^{-7}\frac{M}{s}}{2}\)
\(\frac{-1.565×10^{-6}\frac{M}{s}}{2}\)
\(-7.83×10^-7\frac{M}{s}\)
The instantaneous rate of dimerization is \(-7.83×10^-7\frac{M}{s}\) and the units of this rate is \(\frac{M}{s}\).
3.) The average rate of formation of C8H12 at 1600 s and the instantaneous rate of formation at 3200 s can be found by using our answers from part a and b. If you look back up at the original equation, you could see that C4H6 and C8H12 are related in a two to one ratio. For every two moles of C4H6 used, there is one mole of C8H12 produced.
For this reaction, the average rate of dimerization and the average rate of formation can be linked through this equation:
\(\frac{-1}{2}\frac{\Delta [C_4H_6]}{\Delta t}=\frac{\Delta [C_8H_{12}]}{\Delta t}\)
Notice that reactant side is negative because the reactants are being used up in the reaction.
So, for the average rate of formation of C8H12 at 1600 s, use the rate of dimerization between 0 s and 1600 s we found earlier and plug into the equation:
\(\frac{-1}{2}×3.10 × 10^{-6} \frac{M}{s}=\frac{\Delta [C_8H_{12}]}{\Delta t}\)
\(\frac{\Delta [C_8H_{12}]}{\Delta t}=1.55×10^{-6}\frac{M}{s}\)
The average rate of formation for C8H12 at 1600 s is \(1.55×10^{-6}\frac{M}{s}\). The rate of formation will be positive because products are being formed.
The instantaneous rate of formation for C8H12 can be linked to the instantaneous rate of dimerization by this equation:
\(\frac{-1}{2}\frac{d[C_4H_6]}{dt}=\frac{d[C_8H_{12}]}{dt}\)
So, for the instantaneous rate of formation for C8H12 at 3200 s, use the value of instantaneous rate of dimerization at 3200 s found earlier and plug into the equation:
\(\frac{-1}{2}×-7.83×10^-7\frac{M}{s}=\frac{d[C_8H_{12}]}{dt}\)
\(\frac{d[C_8H_{12}]}{dt}=-3.92×10^{-7}\frac{M}{s}\)
The instantaneous rate of formation for C8H12 at 3200 s is \(-3.92×10^-7\frac{M}{s}\)
- Answer
-
- \(3.10 × 10^{-6} \frac{M}{s}\) and \(1.04 × 10^{-6} \frac{M}{s}\)
- \(-7.83×10^-7\frac{M}{s}\) and \(\frac{M}{s}\)
- \(-3.92×10^-7\frac{M}{s}\)
Q12.1.5
A study of the rate of the reaction represented as \(2A⟶B\) gave the following data:
| Time (s) | 0.0 | 5.0 | 10.0 | 15.0 | 20.0 | 25.0 | 35.0 |
|---|---|---|---|---|---|---|---|
| [A] (M) | 1.00 | 0.952 | 0.625 | 0.465 | 0.370 | 0.308 | 0.230 |
- Determine the average rate of disappearance of A between 0.0 s and 10.0 s, and between 10.0 s and 20.0 s.
- Estimate the instantaneous rate of disappearance of A at 15.0 s from a graph of time versus [A]. What are the units of this rate?
- Use the rates found in parts (a) and (b) to determine the average rate of formation of B between 0.00 s and 10.0 s, and the instantaneous rate of formation of B at 15.0 s.
- Solution
-
Equations: \(\frac{-\bigtriangleup A}{\bigtriangleup time}\) and Rate=\(\frac{-\bigtriangleup A}{2\bigtriangleup time}=\frac{\bigtriangleup B}{time}\)
Solve: 1.)The change in A from 0s to 10s is .625-1=-.375 so \(\frac{-\bigtriangleup A}{\bigtriangleup time}\)=.375/10= 0.0374 M/s
Similarly, the change in A from 10 to 20 seconds is .370-.625=-.255 so \(\frac{-\bigtriangleup A}{\bigtriangleup time}\)=.255/20-10= 0.0255M/s
2.) We can estimate the rate law graphing the points against different order equations to determine the right order.
Zero Order: \[\frac{d[A]}{dt}=-k\nonumber \] \[\int_{A_{\circ}}^{A}d[A]=-k\int_{0}^{t}dt\nonumber \] \[[A]=-kt+[A_{\circ}]\nonumber \]
First Order: \[\frac{d[A]}{dt}=-k[A]\nonumber \] \[\int_{A_{\circ}}^{A}\frac{d[A]}{[A]}=-kdt\nonumber \] \[Ln(A)=-kt+Ln(A_{\circ})\nonumber \]
Second Order: \[\frac{d[A]}{dt}=-k[A]^{2}\nonumber \] \[\int_{A\circ}^{A}\frac{d[A]}{[A]^{2}}=-k\int_{0}^{t}dt\nonumber \]
\[\frac{1}{[A]}=kt+\frac{1}{[A_{\circ}]}\nonumber \]
Now that we have found the linear from of each order we will plot the points vs an [A] y-axis, a Ln(A) y-axis, and a 1/[A] y-axis. whichever of the plots has the most linear points will give us a good idea of the order and the slope will be the k value.
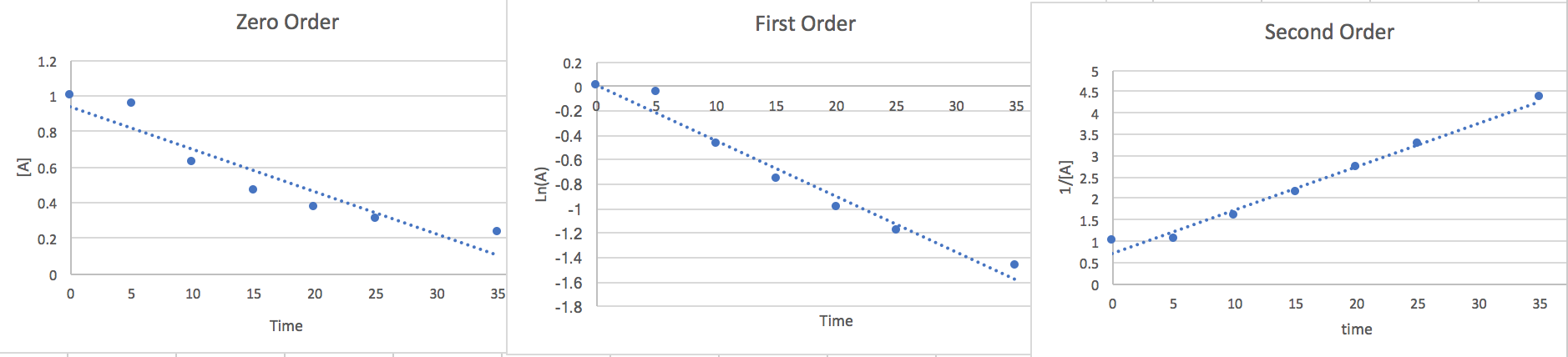
Here we notice that the second order is most linear so we conclude the Rate to be.. \[\frac{-d[A]}{2dt}=k[A]^{2}\nonumber \] At 15 seconds [A]=.465 and from the slope of the graph we find k=.116.so if we plug this data in and multiply both sides by 2 to get rid of the 2 in the denominator on the left side of the equation we find that the rate of disappearance of A is .05 M/s where the units are equivalent to [mol*L-1*s-1]
3.) Using the equation \(\frac{-\bigtriangleup A}{2\bigtriangleup time}=\frac{\bigtriangleup B}{time}\) we divide the rates in part a and b in half to get .0188 M/s from 0 to 10 seconds and .025 M/s for the estimated instantaneous rate at 15s.
- Answer
-
(a) average rate, 0 − 10 s = 0.0375 mol L−1 s−1; average rate, 12 − 18 s = 0.0225 mol L−1 s−1; (b) instantaneous rate, 15 s = 0.0500 mol L−1 s−1; (c) average rate for B formation = 0.0188 mol L−1 s−1; instantaneous rate for B formation = 0.0250 mol L−1 s−1
Q12.1.6
Consider the following reaction in aqueous solution:
\[\ce{5Br-}(aq)+\ce{BrO3-}(aq)+\ce{6H+}(aq)⟶\ce{3Br2}(aq)+\ce{3H2O}(l)\nonumber \]
If the rate of disappearance of Br–(aq) at a particular moment during the reaction is 3.5 × 10−4 M s−1, what is the rate of appearance of Br2(aq) at that moment?
- Solution
-
Step 1. Define the rate of the reaction.
Recall:
For the general reaction: aA + bB → cC+ dD
\(rate =- \frac{\Delta[A]}{a\Delta{t}}=- \frac{\Delta[B]}{b\Delta{t}}= \frac{\Delta[C]}{c\Delta{t}}=\frac{\Delta[D]}{d\Delta{t}}\)
So, for the reaction: \(5Br^−(aq)+BrO^−_3(aq)+6H^+→3Br_2(aq)+3H_2O(l)\)
The rate would be: \(rate =- \frac{\Delta[Br^-]}{5\Delta{t}}=- \frac{\Delta[BrO^-_3]}{\Delta{t}}= -\frac{\Delta[H^+]}{6\Delta{t}}=\frac{\Delta[Br_2]}{3\Delta{t}}=\frac{H_2O}{3\Delta{t}}\)
Step 2. Since we are given the rate for the disappearance of \(Br^-\)(aq) is \(3.5x10^-4 Ms^{-1}\), and we want to find the rate of appearance of \(Br_2\)(aq). Therefore we set the two rates equal to each other.
\(rate =- \frac{\Delta[Br^-]}{5\Delta{t}}= \frac{\Delta[Br_2]}{3\Delta{t}}\)
And,\(-\frac{\Delta[Br^-]}{\Delta{t}}= -3.5x10^{-4} Ms^{-1}\)
So, \(3.5x10^{-4} Ms^{-1}\) = \(\frac{5}{3}\frac{\Delta[Br_2]}{\Delta{t}}\)
Step 3. Now solve the equation.
\(\frac{(3.5x10^{-4})(3)}{5} = \frac{\Delta[Br_2]}{\Delta{t}}\)
\(\frac{\Delta[Br_2]}{\Delta{t}} = 2.1 x 10^{-4} Ms^{-1}\)
- Answer
-
\(\frac{\Delta[Br_2]}{\Delta{t}} = 2.1 x 10^{-4} Ms^{-1}\)
12.2: Factors Affecting Reaction Rates
Q12.2.1
Describe the effect of each of the following on the rate of the reaction of magnesium metal with a solution of hydrochloric acid: the molarity of the hydrochloric acid, the temperature of the solution, and the size of the pieces of magnesium.
- Solution
-
Molarity of Hydrochloric Acid
- Reaction rates are affected by the frequency at which molecules collide. High Molarity=High Concentration which means more molecules are available to collide thus a faster reaction that one with a low molarity of HCl at a fixed volume.
- Higher temperatures increase the rate of reaction because molecules move faster thus colliding more frequently
- increasing temperatures allows for more particles to move past activation energy barrier to start the reaction
- reaction rate is dependent on solid reactant size; smaller pieces increases the chance of collision because they enable a greater surface area thus faster reaction rate
Q12.2.2
Go to the PhET Reactions & Rates interactive. Use the Single Collision tab to represent how the collision between monatomic oxygen (O) and carbon monoxide (CO) results in the breaking of one bond and the formation of another. Pull back on the red plunger to release the atom and observe the results. Then, click on “Reload Launcher” and change to “Angled shot” to see the difference.
- What happens when the angle of the collision is changed?
- Explain how this is relevant to rate of reaction.
- Solution
-
According to the collision theory, there are many factors that cause a reaction to happen, with three of the factors being how often the molecules or atoms collide, the molecules' or atoms' orientations, and if there is sufficient energy for the reaction to happen. So, if the angle of the plunger is changed, the atom that is shot (a lone Oxygen atom in this case) will hit the other molecule (CO in this case) at a different spot and at a different angle, therefore changing the orientation and the number of proper collisions will most likely not cause for a reaction to happen. Thanks to the simulation, we can see that this is true: depending on the angle selected, the atom may take a long time to collide with the molecule and, when a collision does occur, it may not result in the breaking of the bond and the forming of the other (no reaction happens).
In this particular case, the rate of the reaction will decrease because, by changing the angle, the molecules or atoms won't collide with the correct orientation or as often with the correct orientation.
Q12.2.3
In the PhET Reactions & Rates interactive, use the “Many Collisions” tab to observe how multiple atoms and molecules interact under varying conditions. Select a molecule to pump into the chamber. Set the initial temperature and select the current amounts of each reactant. Select “Show bonds” under Options. How is the rate of the reaction affected by concentration and temperature?
S12.2.3
Based on the Collision Theory, a reaction will only occur if the molecules collide with proper orientation and with sufficient energy required for the reaction to occur. The minimum energy the molecules must collide with is called the activation energy (energy of transition state).
Increasing the concentration of reactants increases the probability that reactants will collide in the correct orientation since there are more reactants in the same volume of space. Therefore, increasing the concentration of reactants would increase the rate of the reaction. Decreasing the concentration of reactants would decrease the rate of reaction because the overall number of possible collisions would decrease.
Temperature is directly related the the kinetic energy of molecules and activation energy \(E_a\) is the minimum energy required for a reaction to occur and doesn't change for a reaction. Increasing the temperature increases the kinetic energy of the reactants meaning the reactants will move faster and collide with each other more frequently. Therefore, increasing the temperature increase the rate of the reaction. Decreasing the temperature decreases the rate of reaction since the molecules will have less kinetic energy, move slower, and therefore collide with each other less frequently.
Q12.2.4
In the PhET Reactions & Rates interactive, on the Many Collisions tab, set up a simulation with 15 molecules of A and 10 molecules of BC. Select “Show Bonds” under Options.
- Leave the Initial Temperature at the default setting. Observe the reaction. Is the rate of reaction fast or slow?
- Click “Pause” and then “Reset All,” and then enter 15 molecules of A and 10 molecules of BC once again. Select “Show Bonds” under Options. This time, increase the initial temperature until, on the graph, the total average energy line is completely above the potential energy curve. Describe what happens to the reaction.
- Solution
-
a. On the simulation, we select the default setting and the reaction A+BC. In the default setting, we see frequent collisions, a low initial temperature, and a total average energy lower than the energy of activation. The collision theory states that the rate of a reaction is directly proportional to (the fraction of molecules with required orientation), (fractions of collisions with required energy), and (collision frequency). Although we see moving and frequently colliding reactants, the rate of the forward reaction is actually slow because it takes a long time for the products, AB and C, to start appearing. This is mainly because the fractions of collisions with required energy is low, coming from the average energy of the molecules being lower than the energy of activation.
b. The reaction proceeds at an even faster rate. Again, the collision theory states that the rate of a reaction is directly proportional to (the fraction of molecules with required orientation), (fractions of collisions with required energy), and (collision frequency). Because molecules have a higher amount of energy, they have more kinetic energy. With an increased kinetic energy, the molecules not only collide more but also increase in the fraction of collision. However, the forward reaction and the backward reaction both proceed at a fast rate, so both happen almost simultaneously. It takes a shorter time for both reactions to happen. With both of the reactions adding up together overall, there is eventually a state of equilibrium. The process at which equilibrium is reached, however, is faster. Therefore, the amount of products of A+BC stays the same after a while.
12.3: Rate Laws
Q12.3.1
How do the rate of a reaction and its rate constant differ?
S12.3.1
The rate of a reaction or reaction rate is the change in the concentration of either the reactant or the product over a period of time. If the concentrations change, the rate also changes.
Rate for A → B:
The rate constant (k) is a proportionality constant that relates the reaction rates to reactants. If the concentrations change, the rate constant does not change.
For a reaction with the general equation: \(aA+bB→cC+dD \)
the experimentally determined rate law usually has the following form:
Q12.3.2
Doubling the concentration of a reactant increases the rate of a reaction four times. With this knowledge, answer the following questions:
- What is the order of the reaction with respect to that reactant?
- Tripling the concentration of a different reactant increases the rate of a reaction three times. What is the order of the reaction with respect to that reactant?
- Solution
-
(a) 2; (b) 1
Q12.3.3
Tripling the concentration of a reactant increases the rate of a reaction nine times. With this knowledge, answer the following questions:
- What is the order of the reaction with respect to that reactant?
- Increasing the concentration of a reactant by a factor of four increases the rate of a reaction four times. What is the order of the reaction with respect to that reactant?
Q12.3.4
How much and in what direction will each of the following affect the rate of the reaction: \(\ce{CO}(g)+\ce{NO2}(g)⟶\ce{CO2}(g)+\ce{NO}(g)\) if the rate law for the reaction is \(\ce{rate}=k[\ce{NO2}]^2\)?
- Decreasing the pressure of NO2 from 0.50 atm to 0.250 atm.
- Increasing the concentration of CO from 0.01 M to 0.03 M.
- Solution
-
(a) The process reduces the rate by a factor of 4. (b) Since CO does not appear in the rate law, the rate is not affected.
Q12.3.5
How will each of the following affect the rate of the reaction: \(\ce{CO}(g)+\ce{NO2}(g)⟶\ce{CO2}(g)+\ce{NO}(g)\) if the rate law for the reaction is \(\ce{rate}=k[\ce{NO2}][\ce{CO}]\) ?
- Increasing the pressure of NO2 from 0.1 atm to 0.3 atm
- Increasing the concentration of CO from 0.02 M to 0.06 M.
Q12.3.6
Regular flights of supersonic aircraft in the stratosphere are of concern because such aircraft produce nitric oxide, NO, as a byproduct in the exhaust of their engines. Nitric oxide reacts with ozone, and it has been suggested that this could contribute to depletion of the ozone layer. The reaction \(\ce{NO + O3⟶NO2 + O2}\) is first order with respect to both NO and O3 with a rate constant of 2.20 × 107 L/mol/s. What is the instantaneous rate of disappearance of NO when [NO] = 3.3 × 10−6 M and [O3] = 5.9 × 10−7 M?
- Solution
-
4.3 × 10−5 mol/L/s
Q12.3.7
Radioactive phosphorus is used in the study of biochemical reaction mechanisms because phosphorus atoms are components of many biochemical molecules. The location of the phosphorus (and the location of the molecule it is bound in) can be detected from the electrons (beta particles) it produces:
\[\ce{^{32}_{15}P⟶^{32}_{16}S + e-}\nonumber \]
Rate = 4.85 × 10−2 \(\mathrm{day^{-1}\:[^{32}P]}\)
What is the instantaneous rate of production of electrons in a sample with a phosphorus concentration of 0.0033 M?
Q12.3.8
The rate constant for the radioactive decay of 14C is 1.21 × 10−4 year−1. The products of the decay are nitrogen atoms and electrons (beta particles):
\[\ce{^6_{14}C⟶^{6}_{14}N + e-}\nonumber \]
\[\ce{rate}=k[\ce{^6_{14}C}]\nonumber \]
What is the instantaneous rate of production of N atoms in a sample with a carbon-14 content of 6.5 × 10−9 M?
- Solution
-
7.9 × 10−13 mol/L/year
Q12.3.9
What is the instantaneous rate of production of N atoms Q12.3.8 in a sample with a carbon-14 content of 1.5 × 10−9 M?
Q12.3.10
The decomposition of acetaldehyde is a second order reaction with a rate constant of 4.71 × 10−8 L/mol/s. What is the instantaneous rate of decomposition of acetaldehyde in a solution with a concentration of 5.55 × 10−4 M?
Q12.3.11
Alcohol is removed from the bloodstream by a series of metabolic reactions. The first reaction produces acetaldehyde; then other products are formed. The following data have been determined for the rate at which alcohol is removed from the blood of an average male, although individual rates can vary by 25–30%. Women metabolize alcohol a little more slowly than men:
| [C2H5OH] (M) | 4.4 × 10−2 | 3.3 × 10−2 | 2.2 × 10−2 |
|---|---|---|---|
| Rate (mol/L/h) | 2.0 × 10−2 | 2.0 × 10−2 | 2.0 × 10−2 |
Determine the rate equation, the rate constant, and the overall order for this reaction.
- Solution
-
rate = k; k = 2.0 × 10−2 mol/L/h (about 0.9 g/L/h for the average male); The reaction is zero order.
Q12.3.12
Under certain conditions the decomposition of ammonia on a metal surface gives the following data:
| [NH3] (M) | 1.0 × 10−3 | 2.0 × 10−3 | 3.0 × 10−3 |
|---|---|---|---|
| Rate (mol/L/h1) | 1.5 × 10−6 | 1.5 × 10−6 | 1.5 × 10−6 |
Determine the rate equation, the rate constant, and the overall order for this reaction.
Q12.3.13
Nitrosyl chloride, NOCl, decomposes to NO and Cl2.
\[\ce{2NOCl}(g)⟶\ce{2NO}(g)+\ce{Cl2}(g)\nonumber \]
Determine the rate equation, the rate constant, and the overall order for this reaction from the following data:
| [NOCl] (M) | 0.10 | 0.20 | 0.30 |
|---|---|---|---|
| Rate (mol/L/h) | 8.0 × 10−10 | 3.2 × 10−9 | 7.2 × 10−9 |
- Solution
-
Before we can figure out the rate constant first we must first determine the basic rate equation and rate order. The basic rate equation for this reaction, where n is the rate order of NOCl and k is the rate constant, is
\[rate = k[NOCl]^n\nonumber \]
since NOCl is the reactant in the reaction.
In order to figure out the order of the reaction we must find the order of [NOCl] as it is the only reactant in the reaction. To do this we must examine how the rate of the reaction changes as the concentration of NOCl changes.
As [NOCl] doubles in concentration from 0.10 M to 0.20 M the rate goes from 8.0 x 10-10 to 3.2 x 10-9
(3.2 x 10-9(mol/L/h))/(8.0 x 10-10(mol/L/h)) = 4
so we conclude that as [NOCl] doubles, the rate goes up by 4. Since 22= 4 we can say that the order of [NOCl] is 2 so our updated rate law is
\[rate = k[NOCl]^2\nonumber \]
Now that we have the order, we can substitute the first experimental values from the given table to find the rate constant, k
(8.0 x 10-10(mol/L/h)) = k(0.10 M)2 so
\[k= \dfrac{8.0 \times 10^{-10}}{ (0.10\, M)^2} = 8 \times 10^{-8} M^{-1} sec^{-1}\nonumber \]
We were able to find the units of k using rate order, when the rate order is 2 units of k are M-1 x sec-1
So the rate equation is: rate = k[NOCl]2, it is second order, and k = 8 x 10-8 M-1 x sec-1
Overall rate law : \[rate = \underbrace{(8 \times 10^{-8})}_{\text{1/(M x sec)}} [NOCl]^2\nonumber \]
- Answer
-
rate = k[NOCl]2; k = 8.0 × 10−8 L/mol/s; second order
Q12.3.14
From the following data, determine the rate equation, the rate constant, and the order with respect to A for the reaction \(A⟶2C\).
| [A] (M) | 1.33 × 10−2 | 2.66 × 10−2 | 3.99 × 10−2 |
|---|---|---|---|
| Rate (mol/L/h) | 3.80 × 10−7 | 1.52 × 10−6 | 3.42 × 10−6 |
- Solution
-
A. Using the experimental data, we can compare the effects of changing [A] on the rate of reaction by relating ratios of [A] to ratios of rates
\[ \frac{2.66 \times 10^{-2}}{1.33 \times 10^{-2}} = 2\nonumber \] and \[ \frac{1.52 \times 10^{-6}}{3.8 \times 10^{-7}} = 4\nonumber \]
B. From this we know that doubling the concentration of A will result in quadrupling the rate of reaction. The order of this reaction is 2.
C. We can now write the rate equation since we know the order:
\[rate=k[A]^2\nonumber \]
D. By plugging in one set of experimental data into our rate equation we can solve for the rate constant, k:
\[3.8 \times 10^{-7} = k \times (1.33 \times 10^{-2})^{2}\nonumber \]
\[k = \frac{3.8 \times 10^{-7}}{1.769 \times 10^{-4}}\nonumber \]
\[k= .00215 M^{-1}s^{-1}\nonumber \]
- Answer
-
\(k= .00215 M^{-1}s^{-1}\)
2nd Order
Q12.3.15
Nitrogen(II) oxide reacts with chlorine according to the equation:
\[\ce{2NO}(g)+\ce{Cl2}(g)⟶\ce{2NOCl}(g)\nonumber \]
The following initial rates of reaction have been observed for certain reactant concentrations:
| [NO] (mol/L1) | [Cl2] (mol/L) | Rate (mol/L/h) |
|---|---|---|
| 0.50 | 0.50 | 1.14 |
| 1.00 | 0.50 | 4.56 |
| 1.00 | 1.00 | 9.12 |
What is the rate equation that describes the rate’s dependence on the concentrations of NO and Cl2? What is the rate constant? What are the orders with respect to each reactant?
- Solution
-
For the general equation,
\(aA + bB \rightarrow cC + dD\)
The rate can be written as
\(rate = k[A]^{m}[B]^{n}\) where k is the rate constant, and m and n are the reaction orders.
For our equation
\(2NO(g) + Cl_{2}(g) \rightarrow 2NOCl(g)\)
the \(rate = k[NO]^{m}[Cl_{2}]^{n}\)
Now, we need to find the reaction orders. Reaction orders can only be found through experimental values. We can compare two reactions where one of the reactants has the same concentration for both trials, and solve for the reaction order.
\(\frac{rate_{1}}{rate_{2}}=\frac{[NO]_{1}^{m}[Cl_{2}]_{1}^{n}}{[NO]_{2}^{m}[Cl_{2}]_{2}^{n}}\)
We can use the data in the table provided. If we plug in the values for rows 1 and 2, we see that the values for the concentration of Cl will cancel, leaving just the rates and the concentrations of NO.
\(\frac{1.14}{4.56}=\frac{[0.5]^{m}}{[1.0]^{m}}\)
We can now solve for m, and we find that m =2. This means that the reaction order for [NO] is 2.
Now we must find the value of n. To do so, we can use the same equation but with the values from rows 2 and 3. This time, the concentration of NO will cancel out.
\(\frac{4.56}{9.12}=\frac{[0.5]^{n}}{[1.0]^{n}}\)
When we solve for n, we find that n = 1. This means that the reaction order for [Cl2] is 1.
We are one step closer to finishing our rate equation.
\(rate = k[NO]^{2}[Cl_{2}]\)
Finally, we can solve for the rate constant. To do this, we can use one of the trials of the experiment, and plug in the values for the rate, and concentrations of reactants, then solve for k.
\(1.14 mol/L/h = k[0.5 mol/L]^{2}[0.5mol/L]\)
\(k=9.12L^{2}mol^{-2}h^{-1}\)
So, our final rate equation is:
\(rate = (9.12 L^{2} mol^{-2}h^{-1})[NO]^{2}[Cl_{2}]\)
*A common mistake is forgetting units. Make sure to track your units throughout the process of determining your rate constant. Be careful because the units will change relative to the reaction order.
- Answer
-
rate = k[NO]2[Cl]2; k = 9.12 L2 mol−2 h−1; second order in NO; first order in Cl2
Q12.3.17
Hydrogen reacts with nitrogen monoxide to form dinitrogen monoxide (laughing gas) according to the equation:
\[\ce{H2}(g)+\ce{2NO}(g)⟶\ce{N2O}(g)+\ce{H2O}(g)\nonumber \]
Determine the rate equation, the rate constant, and the orders with respect to each reactant from the following data:
| [NO] (M) | 0.30 | 0.60 | 0.60 |
|---|---|---|---|
| [H2] (M) | 0.35 | 0.35 | 0.70 |
| Rate (mol/L/s) | 2.835 × 10−3 | 1.134 × 10−2 | 2.268 × 10−2 |
- Solution
-
Determine the rate equation, the rate constant, and the orders with respect to each reactant.
The rate constant and the orders can be determined through the differential rate law. The general form of the differential rate law is given below:
aA + bB + cC ==> products
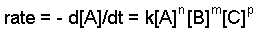
where A, B, and C are the concentrations of the reactants, k is the rate constant, and n,m, and p refer to the order of each reactant.
To find the orders of each reactant, we see that when [NO] doubles but [H2] doesn't change, the rate quadruples, meaning that [NO] is a second order reaction ([NO]2). When [H2] doubles but [NO] doesn't change, the rate doubles, meaning that [H2] is a first order reaction. So the rate law would look something like this:
Rate = k[NO]2[H2]
We can use this rate law to determine the value of the rate constant. Plug in the data for reactant concentration and rate from one of the trials to solve for k the rate constant. In this case, we chose to use the data from trial 1 from the second column of the data table.
2.835x10-3 = k[0.3]2[0.35]
k = .09 M-2/s-1
Q12.3.18
For the reaction \(A⟶B+C\), the following data were obtained at 30 °C:
| [A] (M) | 0.230 | 0.356 | 0.557 |
|---|---|---|---|
| Rate (mol/L/s) | 4.17 × 10−4 | 9.99 × 10−4 | 2.44 × 10−3 |
- What is the order of the reaction with respect to [A], and what is the rate equation?
- What is the rate constant?
- Solution
-
1. The rate equation for an \(n\) order reaction is given as \(\frac{dr}{dt}={k}{[A]^n}\). Where \([A]\) is the concentration in M, and \(\frac{dr}{dt}\) is the rate in M/s.
We can then use each set of data points, plug its values into the rate equation and solve for \(n\). Note you can use any of the data points as long as the concentration corresponds to its rate.
Rate equation 1: \(4.17 \times {10}^{-4}={k}{[0.230]^n}\)
Rate equation 2: \(9.99 \times {10}^{-4}={k}{[0.356]^n}\)
We divide Rate equation 1 by Rate equation 2 in order to cancel out k, the rate constant.
\({\frac{4.17 \times {10}^{-4}}{9.99 \times {10}^{-4}}} = {\frac{k[0.230]^n}{k[0.356]^n}} \)
\({0.417}={0.646^n}\)
Now the only unknown we have is \(n\). Using logarithm rules one can solve for it.
\(ln{\: 0.417}={n \cdot ln{\: 0.646}}\)
\(\frac{ln{\: 0.417}}{ln{\:0.646}}=n=2\)
The rate equation is second order with respect to A and is written as \(\frac{dr}{dt}={k}{[A]^2}\).
2. We can solve for \(k\) by plugging in any data point into our rate equation \(\frac{dr}{dt}={k}{[A]^2}\).
Using the first data points for instance \( [A]=0.230 \:\frac{mol}{L}\) and \( \frac{dr}{dt} = 4.17 \times {10}^{-4} \:\frac{mol}{L \cdot s}\)] we get the equation \(4.17 \times {10}^{-4} \:\frac{mol}{L \cdot s}={k}{[0.230 \:\frac{mol}{L}]^2}\)
Which solves for \(k=7.88 \times {10}^{-3} \frac{L}{mol \cdot s}\)
Since we know this is a second order reaction the appropriate units for \(k\) can also be written as \( \frac{1}{M \cdot s}\)
- Answer
-
(a) The rate equation is second order in A and is written as rate = k[A]2. (b) k = 7.88 × 10−13 L mol−1 s−1
Q12.3.19
For the reaction \(Q⟶W+X\), the following data were obtained at 30 °C:
| [Q]initial (M) | 0.170 | 0.212 | 0.357 |
|---|---|---|---|
| Rate (mol/L/s) | 6.68 × 10−3 | 1.04 × 10−2 | 2.94 × 10−2 |
- What is the order of the reaction with respect to [Q], and what is the rate equation?
- What is the rate constant?
- Solution
-
What is the order of the reaction with respect to [Q], and what is the rate equation?
- Order reaction: 2 because when you use the ratio trial 3:2, it will look like this:
- (\(\dfrac{2.94*10^{-2}}{1.04*10^{-2}}\)) = (\(\dfrac{0.357^{x}}{0.212^{x}}\))
- 2.82 = 1.7x
- x = 2 so the order of reaction is 2
- Rate reaction equation: Rate=k[Q]2
- To find the rate constant (k) simply plug and calculate one of the trials into the rate equation
- 1.04 x 10-2=k[0.212]2
- k=0.231 \(M^{-1}s^{-1}\)
- Answer
-
Order: 2
k=0.231 \(M^{-1}s^{-1}\)
Q12.3.20
The rate constant for the first-order decomposition at 45 °C of dinitrogen pentoxide, N2O5, dissolved in chloroform, CHCl3, is 6.2 × 10−4 min−1.
\[\ce{2N2O5⟶4NO2 + O2}\nonumber \]
What is the rate of the reaction when [N2O5] = 0.40 M?
- Solution
-
Step 1: The first step is to write the rate law. We know the general formula for for a first-order rate law. It is as follows: Rate=k[A]
Step 2: We now plug in [N2O5] in for [A] in our general rate law. We also plug in our rate constant (k), which was given to us. Now our equation looks as follows:
Rate=(6.2x10-4 min-1)[N2O5]
Step 3: We now plug in our given molarity. [N2O5]=0.4 M. Now our equation looks as follows:
Rate=(6.2x10-4 min-1)(0.4 M)
Step 4: We now solve our equation. Rate=(6.2x10-4 min-1)(0.4 M)= 2.48x10-4 M/min.
Step 5: Use significant figures and unit conversion to round 2.48x10-4 M/min to 2.5 × 10−4 (moles)L-1min-1
- Answer
-
(a) 2.5 × 10−4 mol/L/min
Q12.3.21
The annual production of HNO3 in 2013 was 60 million metric tons Most of that was prepared by the following sequence of reactions, each run in a separate reaction vessel.
- \(\ce{4NH3}(g)+\ce{5O2}(g)⟶\ce{4NO}(g)+\ce{6H2O}(g)\)
- \(\ce{2NO}(g)+\ce{O2}(g)⟶\ce{2NO2}(g)\)
- \(\ce{3NO2}(g)+\ce{H2O}(l)⟶\ce{2HNO3}(aq)+\ce{NO}(g)\)
The first reaction is run by burning ammonia in air over a platinum catalyst. This reaction is fast. The reaction in equation (c) is also fast. The second reaction limits the rate at which nitric acid can be prepared from ammonia. If equation (b) is second order in NO and first order in O2, what is the rate of formation of NO2 when the oxygen concentration is 0.50 M and the nitric oxide concentration is 0.75 M? The rate constant for the reaction is 5.8 × 10−6 L2/mol2/s.
- Solution
-
To determine the rate law for an equation we need to look at its slow step. Since both equation a and c are fast, equation b can be considered the slow step of the reaction. The slow step is also considered the rate determining step of the system.
Hence, The rate determining step is the second step because it's the slow step.
rate of production of \(NO_2 = k [A]^m [B]^n \)
\(rate = k [NO]^2 [O_2]^1~M/s\)
\(rate = (5.8*10^{-6}) [0.75]^2 [0.5]^1 ~M/s\)
\(rate = 1.6*10^{-6}~M/s\)
- Answer
-
\(rate = 1.6*10^{-6}~M/s\)
Q12.3.22
The following data have been determined for the reaction:
\[\ce{I- + OCl- ⟶ IO- + Cl-}\nonumber \]
| 1 | 2 | 3 | |
|---|---|---|---|
| \(\mathrm{[I^-]_{initial}}\) (M) | 0.10 | 0.20 | 0.30 |
| \(\mathrm{[OCl^-]_{initial}}\) (M) | 0.050 | 0.050 | 0.010 |
| Rate (mol/L/s) | 3.05 × 10−4 | 6.20 × 10−4 | 1.83 × 10−4 |
Determine the rate equation and the rate constant for this reaction.
- Solution
-
Using the reactants, we can form the rate law of the reaction: $$ r=k[OCl^-]^n[I^-]^m \]
From there, we need to use the data to determine the order of both \([OCl^-]\) and \([I^-]\). In doing so, we need to compare \(r_1\) to \(r_2\) such that:
\[ \frac {r_1}{r_2} = \frac {(0.10^m)(0.050^n)}{(0.20^m)(0.050^n)} = \frac {3.05 \times 10^{-4}}{6.20 \times 10^{-4}} \]
\[ 0.5^m = 0.5 \]
\[ m = 1 \]
We can "cross out" the concentration of \([OCl^-]\) because it has the same concentration in both of the trials used.
Now that we know m (\([I^-]\)) has a first order of 1.
We cannot "cross out" \([I^-]\) to find \([OCl^-]\) because no two trials have the same concentration. In order to solve for n we will plug in 1 for m.
\[ \frac {r_1}{r_3} = \frac {(0.10^{1})(0.050^n)}{(0.30^{1})(0.010^n)} = \frac {3.05 \times 10^{-4}}{1.83 \times 10^{-4}} \]
\[ \frac {1}{3} (5^{n}) = 1.6666667 \]
\[ 5^{n} = 5 \]
\[ n = 1 \]
Since we know that orders of both n and m are equal to one, we can not substitute them into the rate law equation along with the respective concentrations (from either the first, second, or third reaction) and solve for the rate constant, k.
\[ r=k[OCl^-]^n[I^-]^m \]
\[ 3.05 * 10^{-4}= k[0.05]^1[0.10]^1 \]
\[ k = 6.1 * 10^{-2} \frac {L}{mol \times s} \]
Thus the overall rate law is: $$ r = (6.1 * 10^{-2} \frac {L}{mol \times s})[OCl^-][I^-] \]
The units for K depend on the overall order of the reaction. To find the overall order we add m and n together. By doing this we find an overall order of 2. This is why the units for K are $$ \frac {L}{mol \times s} \]
- Answer
-
rate = k[I−][OCl−1]; k = 6.1 × 10−2 L mol −1 s−1
Q12.3.23
In the reaction
\[2NO + Cl_2 → 2NOCl\nonumber \]
the reactants and products are gases at the temperature of the reaction. The following rate data were measured for three experiments:
| Initial p{NO} | Initial p{Cl2} | Initial rate |
|---|---|---|
| (atm) | (atm) | (moles of A consumed atm sec-1) |
| 0.50 | 0.50 | 5.1 x 10-3 |
| 1.0 | 1.0 | 4.0 x 10-2 |
| 0.50 | 1.0 | 1.0 x 10-2 |
- From these data, write the rate equation for this gas reaction. What order is the reaction in NO, Cl2, and overall?
- Calculate the specific rate constant for this reaction.
- Solution
-
a. The rate equation can be determined by designing experiments that measure the concentration(s) of one or more reactants or products as a function of time. For the reaction \(A+B\rightarrow products\), for example, we need to determine k and the exponents m and n in the following equation:
\[rate=k[A]^m[B]^n\nonumber \]
To do this, the initial concentration of B can be kept constant while varying the initial concentration of A and calculating the initial reaction rate. This information would deduce the reaction order with respect to A. The same process can be done to find the reaction order with respect to B.
In this particular example,
\[\frac{rate_2}{rate_3}=\frac{k[A_2]^m[B_2]^n}{k[A_3]^m[B_3]^n}\nonumber \]
So taking the values from the table,
\[\frac{4.0*10^{-2}}{1.0*10^{-2}}=\frac{k[1.0]^m[1.0]^n}{k[0.5]^m[1.0]^n}\nonumber \]
and by canceling like terms, you are left with
\[\frac{4.0*10^{-2}}{1.0*10^{-2}}=\frac{[1.0]^m}{[0.5]^m}\nonumber \]
Now, solve for m
\(4=2^m\Longrightarrow m=2\) Because m=2, the reaction with respect to \(NO\) is 2. \(NO\) is second order.
You can repeat the same process to find n.
\[\frac{rate_3}{rate_1}=\frac{k[A_3]^m[B_3]^n}{k[A_1]^m[B_1]^n}\nonumber \]
Taking the values from the table,
\[\frac{1.0*10^{-2}}{5.1*10^{-3}}=\frac{k[0.5]^m[1.0]^n}{k[0.5]^m[0.5]^n}\nonumber \]
and by canceling like terms, you are left with
\[\frac{1.0*10^{-2}}{5.1*10^{-3}}=\frac{[1.0]^n}{[0.5]^n}\nonumber \]
Now this time, solve for n
\(2=2^n\Longrightarrow n=1\)
Because n=1, the reaction with respect to \(Cl_2\) is 1. \(Cl_2\) is first order.
So the rate equation is\[rate=k[NO]^2[Cl_2]^1\nonumber \]
To find the overall rate order, you simply add the orders together. Second order + first order makes the overall reaction third order.b. The rate constant is calculated by inserting the data from any row of the table into the experimentally determined rate law and solving for k. For a third order reaction, the units of k are \(frac{1}{atm^2*sec}\). Using Experiment 1,
\[rate=k[NO]^2[Cl_2]^1\Longrightarrow 5.1*10^{-3} \frac{atm}{sec}=k[0.5m atm]^2[0.5 atm]^1\nonumber \]
\[k=0.0408 \frac{1}{atm^2*sec}\nonumber \]
- Answer
-
\(NO\) is second order.
\(Cl_2\) is first order.
Overall reaction order is three.
b)
\(k=0.0408\; atm^{-2}*sec^{-1}\)
12.4: Integrated Rate Laws
Q12.4.1
Describe how graphical methods can be used to determine the order of a reaction and its rate constant from a series of data that includes the concentration of A at varying times.
- Solution
-
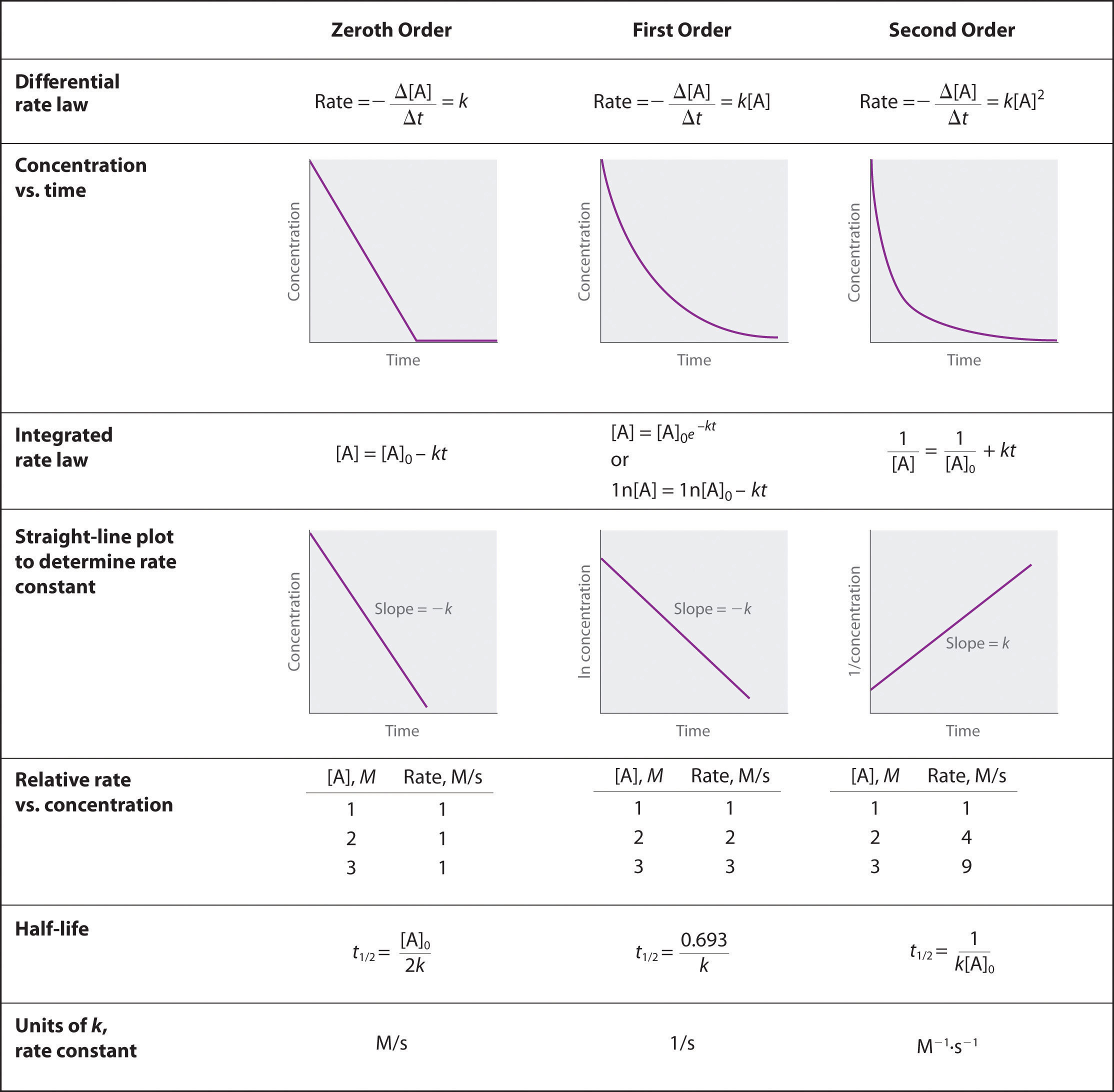
To determine the order of a reaction when given the data series, one must graph the data how it is, graph it as natural log of [A], and graph it as 1/[A]. Whichever method yields a straight line will determine the order. Respective of the methods of graphing above, if a straight line is yielded by the first graphing method its a 0 order, if by the second method it's a 1st order, and the third graphing method its a 2nd order. When the order of the graph is known, a series of equations, given in the above image, can be used with the various points on the graph to determine the value of k. We can see that we need an initial value of A and a final value of A, and both of these would be given by the data.
Zeroth order when plotting initial concentrating versus final concentration you have a negative linear slope.
\[[A] = [A]_0 − kt\nonumber \]
First order when plotting ln[initial concentration] versus ln[ final concentration] you have a negative linear slope.
\[\ln[A] = \ln[A]_0 − kt\nonumber \]
Second order when plotting the 1/[initial concentration] versus 1/[final concentration] you have a positive linear slope.
\[\dfrac{1}{[\textrm A]}=\dfrac{1}{[\textrm A]_0}+kt\nonumber \]
Q12.4.2
Use the data provided to graphically determine the order and rate constant of the following reaction: \(\ce{SO2Cl2 ⟶ SO2 + Cl2}\)
| Time (s) | 0 | 5.00 × 103 | 1.00 × 104 | 1.50 × 104 | 2.50 × 104 | 3.00 × 104 | 4.00 × 104 |
|---|---|---|---|---|---|---|---|
| [SO2Cl2] (M) | 0.100 | 0.0896 | 0.0802 | 0.0719 | 0.0577 | 0.0517 | 0.0415 |
- Solution
-
Use the data to graphically determine the order and rate constant of the following reaction.
In order to determine the rate law for a reaction from a set of data consisting of concentration (or the values of some function of concentration) versus time, make three graphs of the data based on the integrated rate laws of each order reaction.
[concentration] versus time (linear for a zero order reaction) ln [concentration] versus time (linear for a 1st order reaction) 1 / [concentration] versus time (linear for a 2nd order reaction)slope= -2.0 x 10-5
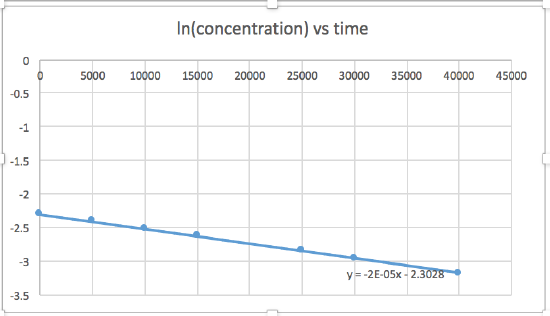
k = 2.0 x 10-5
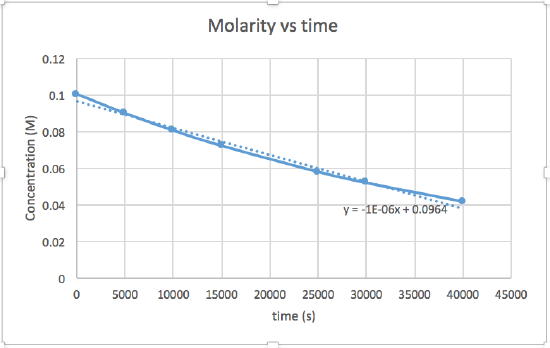
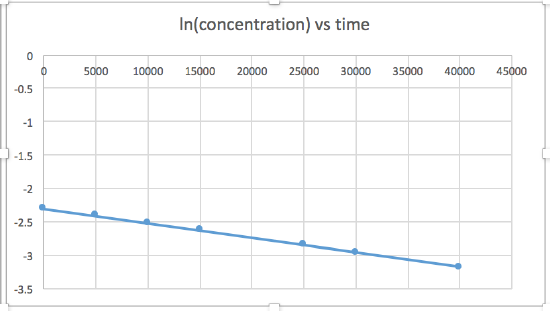
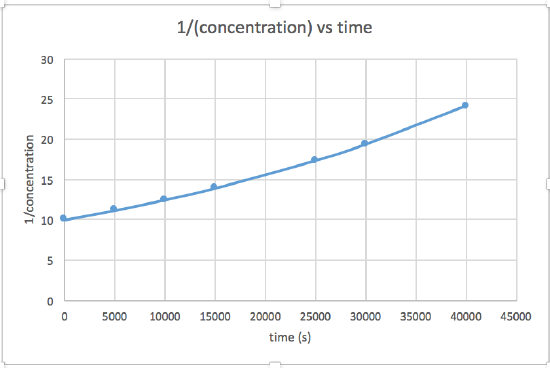
The graph that is linear indicates the order of the reaction. Then, you can find the correct rate equation:
zero order reaction rate = k (k = - slope of line) 1st order reaction rate = k[A] (k = - slope of line) 2nd order reaction rate = k[A]2 (k = slope of line) In this graph, ln(concentration) vs time is linear, indicating that the reaction is first order.
k=-slope of line
- Answer
-
Plotting a graph of ln[SO2Cl2] versus t reveals a linear trend; therefore we know this is a first-order reaction:
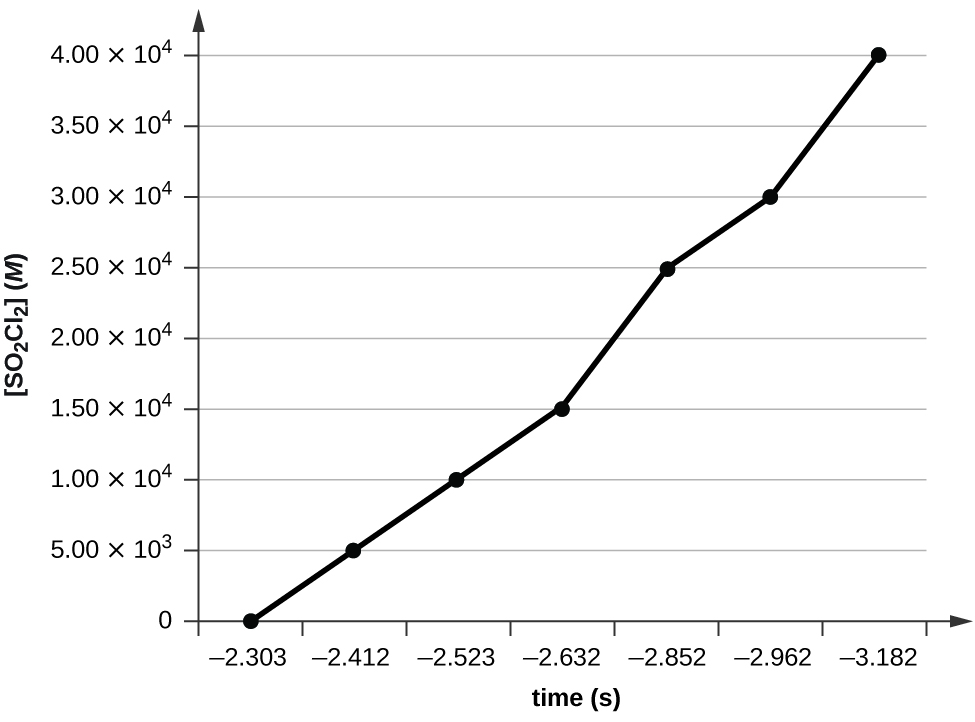
k = −2.20 × 105 s−1
Q12.4.3
Use the data provided in a graphical method to determine the order and rate constant of the following reaction:
\[2P⟶Q+W\nonumber \]
| Time (s) | 9.0 | 13.0 | 18.0 | 22.0 | 25.0 |
|---|---|---|---|---|---|
| [P] (M) | 1.077 × 10−3 | 1.068 × 10−3 | 1.055 × 10−3 | 1.046 × 10−3 | 1.039 × 10−3 |
- Solution
-
Add texts here. Do not delete this text first.
Q12.4.4
Pure ozone decomposes slowly to oxygen, \(\ce{2O3}(g)⟶\ce{3O2}(g)\). Use the data provided in a graphical method and determine the order and rate constant of the reaction.
| Time (h) | 0 | 2.0 × 103 | 7.6 × 103 | 1.23 × 104 | 1.70 × 104 | 1.70 × 104 |
|---|---|---|---|---|---|---|
| [O3] (M) | 1.00 × 10−5 | 4.98 × 10−6 | 2.07 × 10−6 | 1.39 × 10−6 | 1.22 × 10−6 | 1.05 × 10−6 |
- Solution
-
To determine the order and rate constant, you need to graph the data for zero order, first order, and second order by plotting concentration versus time- [A] vs. time, natural logarithm (ln) of [A] vs. time, and 1/[A] vs. time respectively. The order of the reaction is determined by identifying which of these three graphs produces a straight line. The rate constant k is represented by the slope of the graph. The graphs with their respective data values would be
Time (s) 9.0 13.0 18.0 22.0 25.0 [P] (M) 1.077 × 10−3 1.068 × 10−3 1.055 × 10−3 1.046 × 10−3 1.039 × 10−3 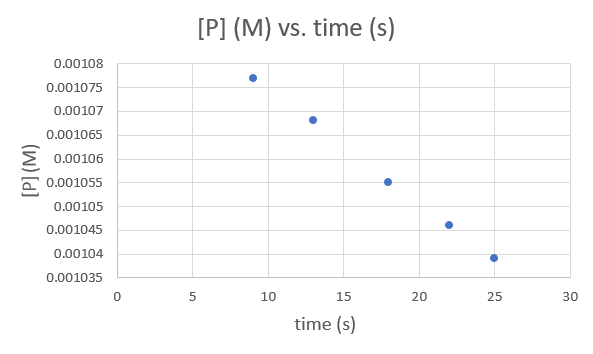.png?revision=1&size=bestfit&width=593&height=354)
Time (s) 9.0 13.0 18.0 22.0 25.0 ln [P] (M) -6.83358 -6.84197 -6.85421 -6.86278 -6.8695 .png?revision=1&size=bestfit&width=592&height=354)
Time (s) 9.0 13.0 18.0 22.0 25.0 1/[P] (M) 928.5051 936.3296 947.8673 956.0229 962.4639 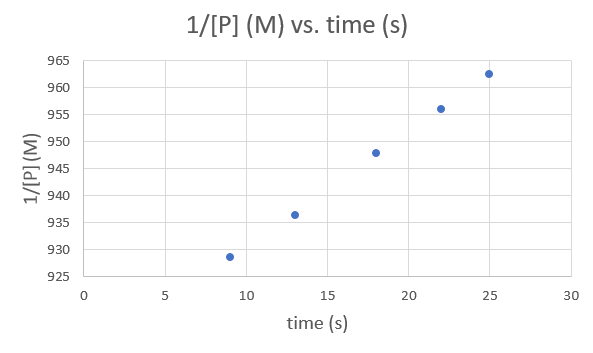.png?revision=1&size=bestfit&width=593&height=353)
Since each graph yields a straight line the order and rate constant of the reaction cannot be determined.
To identify how the concentrations changes a function of time, requires solving the appropriate differential equation (i.e., the differential rate law).
The zero-order rate law predicts in a linear decay of concentration with time
The 1st-order rate law predicts in an exponential decay of concentration with time
The 2nd-order rate law predicts in an reciprocal decay of concentration with time![Time vs [O3].png](https://chem.libretexts.org/@api/deki/files/112236/Time_vs_%255BO3%255D.png?revision=1&size=bestfit&width=564&height=409)
The plot is not linear, so the reaction is not zero order.
![Time vs ln[O3].png](https://chem.libretexts.org/@api/deki/files/112237/Time_vs_ln%255BO3%255D.png?revision=1&size=bestfit&width=570&height=414)
The plot is not linear, so the reaction is not first order.
![Time vs 1over[O3].png](https://chem.libretexts.org/@api/deki/files/112240/Time_vs_1over%255BO3%255D.png?revision=1&size=bestfit&width=608&height=441)
The plot is nicely linear, so the reaction is second order.
To a second order equation, \( 1/[A] \ = k*t + 1/[A_0] \)
Thus, the value of K is the slope of the graph Time vs \( \frac{1}{\ce{O3}}\),
k = 50.3*10^6 L mol−1 h−1
- Answer
-

The plot is nicely linear, so the reaction is second order.
k = 50.1 L mol−1 h−1
Q12.4.5
From the given data, use a graphical method to determine the order and rate constant of the following reaction:
\[2X⟶Y+Z\]
| Time (s) | 5.0 | 10.0 | 15.0 | 20.0 | 25.0 | 30.0 | 35.0 | 40.0 |
|---|---|---|---|---|---|---|---|---|
| [X] (M) | 0.0990 | 0.0497 | 0.0332 | 0.0249 | 0.0200 | 0.0166 | 0.0143 | 0.0125 |
- Solution
-
In order to determine the order of the reaction we need to plot the data using three different graphs. All three graphs will have time in seconds as the x-axis, but the y-axis is what will differ. One graph will plot concentration versus time, the second will plot natural log of concentration versus time, and the other will plot 1/concentration versus times. Whichever graph results in a line, we know that must be the order of the reaction. If we get a line using the first graph, it will be zero order, if it is a line for the second graph it will be first order, and if it is a line for the third graph it will be a second order reaction. Now lets plot the data to determine the order.
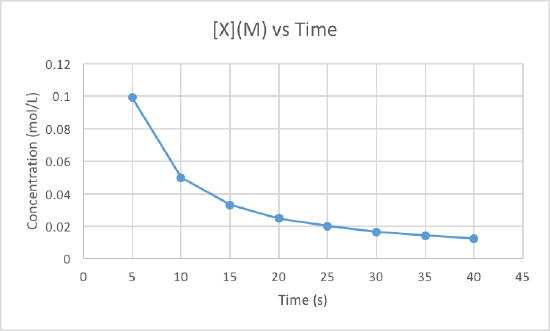
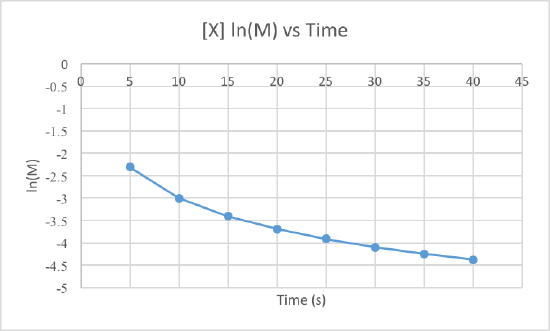
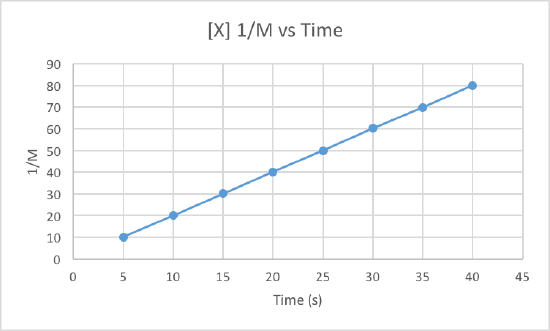
We can clearly see that the third graph, which plots 1/M versus time, is a straight line while the other two are slightly curved. Therefore, we can determine that the rate of this reaction is second order. This also tells us that the units of the rate constant which should be M-2s-1 for a second order reaction.
To determine the rate constant, called k, we simple need to figure out the slope of the third graph since that is the order of this reaction. To find the slope of the line, we take two points and subtract the y values and then divide them by the difference of the x values. This is how to do it:
Use the points (5, 10.101) and (40, 80).
Now use these to get the slop, aka the rate constant: (80-10.101)/(40-5) = 1.997 = k
So the rate constant for this second order reaction is 1.997 M-1s-1.
Q12.4.6
What is the half-life for the first-order decay of phosphorus-32? \(\ce{(^{32}_{15}P⟶^{32}_{16}S + e- )}\) The rate constant for the decay is 4.85 × 10−2 day−1.
- Solution
-
This is a first order reaction, so we can use our half life equation below:
\[t_{1/2}=\frac{0.693}{k}\nonumber \]
The rate constant is given to us in units per day. All we have to do, is to plug it into the equation.
\[t_{1/2}=\frac{0.693}{4.85*10^{-2}}\nonumber \]
\[=14.3\; days\nonumber \]A12.4.6
14.3 d
Q12.4.7
What is the half-life for the first-order decay of carbon-14? \(\ce{(^6_{14}C⟶^7_{14}N + e- )}\) The rate constant for the decay is 1.21 × 10−4 year−1.
- Solution
-
To find the half life, we need to use the first-order half-life equation. All half life reactions undergo first order reactions.
The half-life equation for first order is \[t_{1/2}=ln2/k \nonumber \]with k being the rate constant. The rate constant for carbon-14 was given as \(1.21 × 10^{-4} year^{−1}\).
Plug it in the equation. \[t_{1/2}=ln2/(1.21 × 10^{−4} year^{−1})\nonumber \] and solve for \( t_{1/2}\).
When you calculate it, the half life for carbon-14 is 5.73*103
- Answer
-
The half-life for carbon-14 is calculated to be 5.73*103
Q12.4.8
What is the half-life for the decomposition of NOCl when the concentration of NOCl is 0.15 M? The rate constant for this second-order reaction is 8.0 × 10−8 L/mol/s.
- Solution
-
The half-life of a reaction, t1/2, is the amount of time that is required for a reactant concentration to decrease by half compared to its initial concentration. When solving for the half-life of a reaction, we should first consider the order of reaction to determine it's rate law. In this case, we are told that this reaction is second-order, so we know that the integrated rate law is given as:
\[\dfrac{1}{[A]} = kt + \dfrac{1}{[A]_0}\nonumber \]
Isolating for time, we find that:
\[t_{1/2} = \dfrac{1}{k[A]_0}\nonumber \]
Now it is just a matter of substituting the information we have been given to calculate \(t_{1/2}\), where the rate constant, \({k}\), is equal to 8.0 × 10−8 L/mol/s and initial concentration, \({[A]_0}\), is equal to 0.15M:
\[t_{1/2} = \dfrac{1}{(8.0×10^{-8})(0.15)} = {8.33×10^7 seconds}\nonumber \]
- Answer
-
8.33 × 107 s
Q12.4.9
What is the half-life for the decomposition of O3 when the concentration of O3 is 2.35 × 10−6 M? The rate constant for this second-order reaction is 50.4 L/mol/h.
- Solution
-
Add texts here. Do not delete this text first.
Since the reaction is second order, its half-life is
\[t_{1/2}=\dfrac{1}{(50.4M^{-1}/h)[2.35×10^{-6}M]}\nonumber \]
So, half-life is 8443 hours.
Q12.4.10
The reaction of compound A to give compounds C and D was found to be second-order in A. The rate constant for the reaction was determined to be 2.42 L/mol/s. If the initial concentration is 0.500 mol/L, what is the value of t1/2?
- Solution
-
As mentioned in the question the reaction of compound A will result in the formation of compounds C and D. This reaction was found to be second-order in A. Therefore, we should use the second order equation for half-life which relates the rate constant and initial concentrations to the half-life:
\[t_{\frac{1}{2}}=\frac{1}{k[A]_{0}}\nonumber \]
Since we were given k (rate constant) and Initial concentration of A, we have everything needed to calculate the half life of A.
\[k=0.5\frac{\frac{L}{mol}}{s}\nonumber \]
\[[A]_{0}=2.42\frac{mol}{L}\nonumber \]
When we plug in the given information notice that the units cancel out to seconds.
\[t_{\frac{1}{2}}=\frac{1}{\frac{2.42Lmol^{-}}{s}[0.500\frac{mol}{L}]}=0.826 s\nonumber \]
- Answer
-
0.826 s
Q12.4.11
The half-life of a reaction of compound A to give compounds D and E is 8.50 minutes when the initial concentration of A is 0.150 mol/L. How long will it take for the concentration to drop to 0.0300 mol/L if the reaction is (a) first order with respect to A or (b) second order with respect to A?
- Solution
-
Organize the given variables:
(half-life of A) \(t_{1/2}=8.50min\)
(initial concentration of A) \([A]_{0}=0.150mol/L\)
(target concentration of A) \([A]=0.0300mol/L\)Find the the rate constant k, using the half-life formulas for each respective order. After finding k, use the integrated rate law respective to each order and the initial and target concentrations of A to find the time it took for the concentration to drop.
(a) first order with respect to A
(half-life) \(t_{1/2}=\frac{ln(2)}{k}=\frac{0.693}{k}\)
(rearranged for k) \(k=\frac{0.693}{t_{1/2}}\)
(plug in t1/2 = 8.50 min) \(k=\frac{0.693}{8.50min}=0.0815min^{-1}\)(integrated rate law) \(ln[A]=-kt+ln[A]_{0}\)
(rearranged for t) \(ln(\frac{[A]}{[A]_{0}})=-kt\)
\(-ln(\frac{[A]}{[A]_{0}})=kt\)
\(ln(\frac{[A]}{[A]_{0}})^{-1}=kt\)
\(ln(\frac{[A]_{0}}{[A]})=kt\)
\(t=\frac{ln(\frac{[A]_{0}}{[A]})}{k}\)
(plug in variables) \(t=\frac{ln(\frac{0.150mol/L}{0.0300mol/L})}{0.0815min^{-1}}=\frac{ln(5.00)}{0.0815min^{-1}}=19.7min\)(b) second order with respect to A
(half-life) \(t_{1/2}=\frac{1}{k[A]_{0}}\)
(rearranged for k) \(k=\frac{1}{t_{1/2}[A]_{0}}\)
(plug in variables) \(k=\frac{1}{(8.50min)(0.150mol/L)}=\frac{1}{1.275min\cdot mol/L}=0.784L/mol\cdot min\)(integrated rate law) \(\frac{1}{[A]}=kt+\frac{1}{[A]_{0}}\)
(rearranged for t) \(\frac{1}{[A]}-\frac{1}{[A]_{0}}=kt\)
\(t=\frac{1}{k}(\frac{1}{[A]}-\frac{1}{[A]_{0}})\)
(plug in variables) \(t=\frac{1}{0.784L/mol\cdot min}(\frac{1}{0.0300mol/L}-\frac{1}{0.150mol/L})=\frac{1}{0.784L/mol\cdot min}(\frac{80}{3}L/mol)=34.0min\)
- Answer
-
a) 19.7 min
b) 34.0 min
Q12.4.12
Some bacteria are resistant to the antibiotic penicillin because they produce penicillinase, an enzyme with a molecular weight of 3 × 104 g/mol that converts penicillin into inactive molecules. Although the kinetics of enzyme-catalyzed reactions can be complex, at low concentrations this reaction can be described by a rate equation that is first order in the catalyst (penicillinase) and that also involves the concentration of penicillin. From the following data: 1.0 L of a solution containing 0.15 µg (0.15 × 10−6 g) of penicillinase, determine the order of the reaction with respect to penicillin and the value of the rate constant.
| [Penicillin] (M) | Rate (mol/L/min) |
|---|---|
| 2.0 × 10−6 | 1.0 × 10−10 |
| 3.0 × 10−6 | 1.5 × 10−10 |
| 4.0 × 10−6 | 2.0 × 10−10 |
- Solution
-
The first step is to solve for the order or the reaction. This can be done by setting up two expressions which equate the rate to the rate constant times the molar concentration of penicillin raised to the power of it's order. Once we have both expressions set up, we can divide them to cancel out k (rate constant) and use a basic logarithm to solve for the exponent, which is the order. It will look like this.
rate(mol/L/min)=k[M]x
(1.0 x 10-10)=k[2.0 x 10-6]x
(1.5 x 10-10)=k[3.0 x 10-6]x
Dividing the two equations results in the expression:
(2/3)=(2/3)x
*A single ratio equation can also be set up to solve for the reaction order:
*\[\frac{rate_{1}}{rate_{2}}=\frac{k[Penicillin]_{1}^{x}}{k[Penicillin]_{2}^{x}}\nonumber \]
*We then solve for x in a similar fashion.
*\[\frac{1.0x10^{-10}}{1.5x10^{-10}}=\frac{[2.0x10^{-6}]^{x}}{[3.0x10^{-6}]^{x}}\nonumber \]
We can now use the natural logarithm to solve for x, or simply and intuitively see that in order for the equation to work, x must be equal to one. Thus, the reaction is of the first order.
Now that we have the order of the reaction, we can proceed to solve for the value of the rate constant. Substituting x=1 into our first equation yields the expression:(1 x 10-10)=k[2.0 x 10-6]1
k=(1 x 10-10)/(2 x 10-6)
k= (5 x 10-5) min-1
We have a unit of min-1 because we divided (mol/L/min) by molarity, which is in (mol/L), yielding a unit of min-1.
We were given two important pieces of information to finish the problem. It is stated that the enzyme has a molecular weight of 3 × 104 g/mol, and that we have a one liter solution that contains (0.15 x 10-6 g) of penicillinase. Dividing the amount of grams by the molecular weight yields 5 x 10-12 moles.
(0.15 x 10-6) g / (3 x 104) g/mol = (5 x 10-12) mol
Now that we have the amount of moles, we can divide our rate constant by this value.
(5 x 10-5) min-1 / (5 x 10-12) mol = (1 x 107) mol-1 min -1
Answer
-
The reaction is first order with k = 1.0 × 107 mol−1 min−1
Q12.4.13
Both technetium-99 and thallium-201 are used to image heart muscle in patients with suspected heart problems. The half-lives are 6 h and 73 h, respectively. What percent of the radioactivity would remain for each of the isotopes after 2 days (48 h)?
- Solution
-
This problem is asking us for the percentage of radioactivity remaining after a certain time for both isotopes after 48 hours. We must identify an equation that will help us solve this and we can determine that we can determine this information using the first order equation.
This equation Ln(N/No)= -kt tells that the Natural log of the fraction remaining is equal to the rate constant times time. To determine the rate constant, we can also compute .693 over the half-life given in the information.
For Technetium-99 we can determine the rate constant by plugging into the second equation: .693/6 hrs= .1155 h-1
Now that we have the rate constant we can plug in : Ln(N/No)=-(.1155h-1)(48h) so Ln(N/No)=-5.544 and if we take the inverse of the natural log, we get (N/No)=3.9x10 -3 and if we multiply this by 100, we get .39% remaining.
We can do this same process for Thallium-201 and plugin: .693/73 hrs= .009493151 h-1 and when we plug this into the first order equation we get:
Ln(N/No)=-(.009493h-1)(48h) so Ln(N/No)=-.45567248 and when we take the inverse of the natural log, we get (N/No)=.6340 and when multiplied by 100, we get 63.40% remaining which makes sense since its half-life is 73 hours and only 48 hours have passed, half of the amount has yet to be consumed.
- Answer
-
Technetium-99: 0.39%
Thallium-201: 63.40%
Q12.4.14
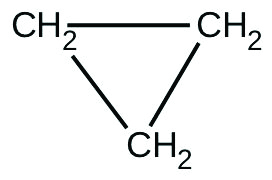
There are two molecules with the formula C3H6. Propene, \(\ce{CH_3CH=CH_2}\), is the monomer of the polymer polypropylene, which is used for indoor-outdoor carpets. Cyclopropane is used as an anesthetic:
When heated to 499 °C, cyclopropane rearranges (isomerizes) and forms propene with a rate constant of 5.95 × 10−4 s−1. What is the half-life of this reaction? What fraction of the cyclopropane remains after 0.75 h at 499 °C?
- Solution
-
Use the equation \[ t{_1}{_/}{_2} = \frac{ln2} k\nonumber \] since this is a first-order reaction. You can tell that this is a first order reaction due to the units of measurement of the rate constant, which is s-1. Different orders of reactions lead to different rate constants, and a rate constant of s-1 will always be first order.
Plug into the equation, and you get half life = 1164.95 seconds. To convert this to hours, we would divide this number by 3600 seconds/hour, to get 0.324 hours.
Use the integrated first order rate law \[ln\frac{[A]}{[A]_0} = -kt\nonumber \]. In this equation, [A]0 represents the initial amount of compound present at time 0, while [A] represents the amount of compound that is left after the reaction has occurred. Therefore, the fraction \[\frac{[A]}{[A]_0}\nonumber \] is equal to the fraction of cyclopropane that remains after a certain amount of time, in this case, 0.75 hours.
Substitute x for the fraction of \[\frac{[A]}{[A]_0}\nonumber \] into the integrated rate law: \[ln\frac{[A]}{[A]_0} = -kt\nonumber \] \[ln(x) = -5.95x10^{-4}(0.75)\nonumber \] \[x=e^{(-0.000595)(0.75)}\nonumber \] = 0.20058 = 20%.
So, the half life is 0.324 hours, and 20% of the cyclopropane will remain as 80% will have formed propene.
- Answer
-
0.324 hours. ; 20% remains
Q12.4.16
Fluorine-18 is a radioactive isotope that decays by positron emission to form oxygen-18 with a half-life of 109.7 min. (A positron is a particle with the mass of an electron and a single unit of positive charge; the nuclear equation is \(\ce{^{18}_9F ⟶ _8^{18}O + ^0_{1}e^+}\).) Physicians use 18F to study the brain by injecting a quantity of fluoro-substituted glucose into the blood of a patient. The glucose accumulates in the regions where the brain is active and needs nourishment.
- What is the rate constant for the decomposition of fluorine-18?
- If a sample of glucose containing radioactive fluorine-18 is injected into the blood, what percent of the radioactivity will remain after 5.59 h?
- How long does it takFe for 99.99% of the 18F to decay?
- Solution
-
a) The nuclear decay of an isotope of an element is represented by the first order equation:
ln(N/N0) = −kt
Where t is time, N0 is the initial amount of the substance, N is the amount of the substance after time t, and k is the rate constant. We can rearrange the equation and isolate k so that we could solve for the rate constant:
k = [-ln(N/N0)] / t
We are given that fluorine-18 has a half-life of 109.7 minutes. Since we have the half-life, we can choose an arbitrary value for N0 and use half of that value for N. In this case, we choose 100 for N0 and 50 for N. Now we can plug in those values into the equation above and solve for k.
k = [-ln(50/100)] / 109.7
k = 0.6931 / 109.7 = 0.006319 min-1
The rate constant for this reaction is 0.006319 min-1.
b) For this problem, we are able to use the same equation from part a:
ln(N/N0) = −kt
However, this time we are given the amount of time elapsed instead of the half-life, and we are asked to determine the percent of fluorine-18 radioactivity remaining after that time. In this problem, we must plug in values for N0, k (determined from part a), and t.
But first, since we are given the elapsed time in hours, we must convert it into minutes:
5.59 hours x (60 minutes / 1 hours) = 335.4 minutes
This gives us the value for t. We also have values for k (0.006319 min-1) and N0 (again an arbitrary number.) Now we can plug values into the original equation, giving us:
ln(N/100) = −(0.006319)(335.4)
We solve this equation by taking the exponential of both sides:
eln(N/100) = e−(0.006319)(335.4)
where eln equals 1 and now we can just solve for N:
N/100 = e−(0.006319)(335.4)
N = [e−(0.006319)(335.4)] x 100 = 12.0
Since 100 was used as the initial amount and 12.0 was determined as the remaining amount, 12.0 can be used as the percentage of remaining amount of radioactivity of fluorine-18. Thus the percent of fluorine-18 radioactivity remaining after 5.59 hours is 12.0%.
c) This part of the question is much like the previous two parts, but this time we are given the initial amount of radioactivity, the final amount of radioactivity and we are asked do determine how long it took for that amount of radioactivity to decay. We are able to use the same equation:
ln(N/N0) = −kt
However, now we are given N and N0 and we have already determined k from before. We are told that 99.99% of the radioactivity has decayed, so we can use 100 and 0.01 for N0 and N respectively. We plug these values in to the equation, solve for t, and get
ln(0.01/1000) = −0.006319t
-9.21 = −0.006319t
t = 1458 minutes
Therefore, its takes 1458 minutes for 99.99% of the radioactivity to decay.
- Answer
-
a) 0.006319 min-1
b) 12.0%
c) 1458 minutes
Q12.4.17
Suppose that the half-life of steroids taken by an athlete is 42 days. Assuming that the steroids biodegrade by a first-order process, how long would it take for \(\dfrac{1}{64}\) of the initial dose to remain in the athlete’s body?
- Solution
-
252 days
for first order reaction: t1/2 = 0.693 / k
k = 0.693 / 42
k = 0.0165
for first order reaction: [A] = [A]0 e-kt
1/64 initial means that: [A] = 1/64 [A]0
therefore: 1/64 [A]0 = [A]0 e-0.0165t
t = 252 days
Q12.4.18
Recently, the skeleton of King Richard III was found under a parking lot in England. If tissue samples from the skeleton contain about 93.79% of the carbon-14 expected in living tissue, what year did King Richard III die? The half-life for carbon-14 is 5730 years.
- Solution
-
In order to find out what year King Richard III died, set [A]/[A0] (the percent of carbon-14 still contained) equal to 0.5time(t)/half life (t1/2) or use the equation N(t) = N0e-rt.
Using the first equation:
\(A/A_{0}\) = \(0.5^{t/t_{1/2}}\) plug in the given numbers \(.9379 = 0.5^{t/5730}\) and solve for t.
\(ln.9379\) = \((t/5730)(ln0.5)\) (using the rule of logs)
\(-.0641\) = \((t/5730)(-.693)\)
\(-367.36\) = \(-.693t\)
\(t = 530.1 years\)
Using \(N(t) = N_{0}e^{-rt}\) this problem is solved by the following:
\(1/2 = e^{-5730r}\)
\(r = 0.000121\)
Now that we know what r is, we can use this value in our original formula and solve for t, the amount of years that have passed.
This time, we use 93.78, the percent of the carbon-14 remaining as N(t) and 100 as the original, N0.
\(93.78 = 100e^{-0.000121t}\)
\(t = 530.7\) years
Another way of doing this is by using these two equations:
λ = \(\dfrac{0.693}{t_{1/2}}\) and \(\dfrac{n_{t}}{n_{0}}\) = -λt
\(n_{t}\) = concentration at time t (93.79)
\(n_{0}\) = initial concentration (100)
First solve for lambda or the decay constant by plugging in the half life.
Then plug in lambda and the other numbers into the second equation, and solve for t- which should equal to 530.1 years as well.
If we want to find out what year King Richard III died, we take the current year, 2017, and subtract 530 years. Doing this, we find that King Richard III died in the year 1487.
- Answer
-
King Richard III died in the year 1487
Q12.4.19
Nitroglycerine is an extremely sensitive explosive. In a series of carefully controlled experiments, samples of the explosive were heated to 160 °C and their first-order decomposition studied. Determine the average rate constants for each experiment using the following data:
| Initial [C3H5N3O9] (M) | 4.88 | 3.52 | 2.29 | 1.81 | 5.33 | 4.05 | 2.95 | 1.72 |
|---|---|---|---|---|---|---|---|---|
| t (s) | 300 | 300 | 300 | 300 | 180 | 180 | 180 | 180 |
| % Decomposed | 52.0 | 52.9 | 53.2 | 53.9 | 34.6 | 35.9 | 36.0 | 35.4 |
- Solution
-
First we need to understand what the question is asking for: the average rate constant. The average rate constant is the variable "k" when discussing kinetics and it can be defined as the proportionality constant in the equation that expresses the relationship between the rate of a chemical reaction and the concentrations of the reacting substances. Knowing that we need to find K in this first order reaction, we can look to formulas that include "k," initial and final concentrations \([A]_o and [A]_t\), and half life time "t." Since this is a first order reaction, we can look to the first order equations, and doing that we find one that includes the variables given in the question: \[\ln[A]_t=-kt+\ln[A]_o\nonumber \]
For the first reaction, we have an initial concentration of 4.88 M, and a percentage decomposed. To find the final concentration, we must multiply the initial concentration by the percentage decomposed to know how much decomposed, and subtract that from the original to find out how much is left: 4.88M x 0.52= 2.54 M and 4.88M-2.54M=2.34M
Now, we have the variables we need, and we plug it into the equation above:
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[2.34M]=-k(300s)+\ln[4.88M]\)
k=\({-(\ln[2.34M]-\ln[4.88M])}\over 300\)
\(k=2.45x10^{-3}\)
Since it asks for the rate constant of each experiment, we now must do the same procedure for each data set to find the rate constant:
Second experiment
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[1.66M]=-k(300s)+\ln[3.52M]\)
k=\({-(\ln[1.66M]-\ln[3.52M])}\over 300\)
\(k=2.51x10^{-3}\)
Third experiment
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[1.07M]=-k(300s)+\ln[2.29M]\)
k=\({-(\ln[1.07M]-\ln[2.29M])}\over 300\)
\(k=2.54x10^{-3}\)
Fourth experiment
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[0.834M]=-k(300s)+\ln[1.81M]\)
k=\({-(\ln[0.834M]-\ln[1.81M])}\over 300\)
\(k=2.58x10^{-3}\)
Fifth Experiment
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[3.49M]=-k(180s)+\ln[5.33M]\)
k=\({-(\ln[3.49M]-\ln[5.33M])}\over 180\)
\(k=2.35x10^{-3}\)
Sixth Experiment
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[2.60M]=-k(180s)+\ln[4.05M]\)
k=\({-(\ln[2.60M]-\ln[4.05M])}\over 180\)
\(k=2.46x10^{-3}\)
Seventh Experiment
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[1.89M]=-k(180s)+\ln[2.95M]\)
k=\({-(\ln[1.89M]-\ln[2.95M])}\over 180\)
\(k=2.47x10^{-3}\)
Eighth experiment
\(\ln[A]_t=-kt+\ln[A]_o\)
\(\ln[1.11M]=-k(180s)+\ln[1.72M]\)
k=\({-(\ln[1.11M]-\ln[1.72M])}\over 180\)
\(k=2.43x10^{-3}\)
- Answer
-
[A]0 (M) k × 103 (s−1) 4.88 2.45 3.52 2.51 2.29 2.54 1.81 2.58 5.33 2.35 4.05 2.44 2.95 2.47 1.72 2.43
Q12.4.20
For the past 10 years, the unsaturated hydrocarbon 1,3-butadiene \(\ce{(CH2=CH–CH=CH2)}\) has ranked 38th among the top 50 industrial chemicals. It is used primarily for the manufacture of synthetic rubber. An isomer exists also as cyclobutene:
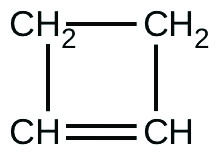
The isomerization of cyclobutene to butadiene is first-order and the rate constant has been measured as 2.0 × 10−4 s−1 at 150 °C in a 0.53-L flask. Determine the partial pressure of cyclobutene and its concentration after 30.0 minutes if an isomerization reaction is carried out at 150 °C with an initial pressure of 55 torr.
- Solution
-
Since this is a first order reaction, the integrated rate law is: \([A_{t}]=[A_{0}]e^{-kt}\)
Partial Pressure: Use the integrated rate law to find the partial pressure at 30 minutes:Use \(A_0\) = 55 torr, t = 30 min, and k = \(2.0 * 10^{-4}s^{-1}\) to solve the integrated rate law equation:
\([A_{30}]=(55 torr)*e^{-(2.0x10^{-4}\frac{1}{sec})(30min\cdot\frac{60sec}{1 min})}\)
Solve this equation to get:
\([A_{30}]=(55 torr)*e^{-0.36}\)
\(A_{30}]\) = 38.37 torr.
Initial Concentration: Find the initial concentration using the ideal gas law.
The ideal gas law is given by \(PV = nRT → n = \frac{PV}{RT}\). Use this form of the gas law to solve for the initial concentration n.
Use V = 0.53L, R = 0.08206 \(\frac{L*atm}{mol*L}\), T = 423.15 K, and P = \(\frac{1 atm}{760}\) = 0.07237 atm .
Solve the ideal gas equation using these values:
\(n=\frac{(55torr)(0.53L)}{(0.08206\frac{L*atm}{mol*K})(423.15K)} = 0.00110\) moles cyclobutene.
Now find the initial concentration of cyclobutene \(A_0\) using the equation \([A_0] = \frac{n}{V}\):
\(A_0 = \frac{n}{V} = \frac{0.00110 moles}{0.53 L} = 0.00208 M\)
Concentration at 30 minutes: Find the concentration of cyclobutene at 30 minutes by using the integrated rate law given above, using time t = 30 minutes, or 1800 seconds.
\([A_{30}]=(0.00208M)e^{-0.36}= 0.00145M\)
So at 30 minutes, the cyclobutene concentration is 0.00145 M, and the partial pressure is 38.37 torr.
- Answer
-
Partial Pressure: 38.37 torr.
Concentration: 0.00145 M
12.5: Collision Theory
Q12.5.1
Chemical reactions occur when reactants collide. What are two factors that may prevent a collision from producing a chemical reaction?
- Solution
-
The two factors that may prevent a collision from producing a chemical reaction are:
1. Kinetic energy of the molecule
In order for chemical reactions to occur, molecules require enough velocity to overcome the minimum activation energy needed to break the old bonds and form new bonds with other molecules. At higher temperatures, the molecules possess the minimum amount of kinetic energy needed which ensures the collisions will be energetic enough to lead to a reaction.
2. The orientation of molecules during the collision
Two molecules have to collide in the right orientation in order for the reaction to occur. Molecules have to orient properly for another molecule to collide at the right activation state.
Q12.5.2
When every collision between reactants leads to a reaction, what determines the rate at which the reaction occurs?
- Solution
-
There has to be contact between reactants for a reaction to occur. The more the reactants collide, the more often reactions can occur. Factors that determine reaction rates include concentration of reactants, temperature, physical states of reactants, surface area, and the use of a catalyst. The reaction rate usually increases as the concentration of a reactant increases. Increasing the temperature increases the average kinetic energy of molecules, causing them to collide more frequently, which increases the reaction rate. When two reactants are in the same fluid phase, their particles collide more frequently, which increases the reaction rate. If the surface area of a reactant is increased, more particles are exposed to the other reactant therefore more collisions occur and the rate of reaction increases. A catalyst participates in a chemical reaction and increases the reaction rate without changing itself.
Q12.5.3
What is the activation energy of a reaction, and how is this energy related to the activated complex of the reaction?
- Solution
-

Activation energy is the energy barrier that must be overcome in order for a reaction to occur. To get the molecules into a state that allows them to break and form bonds, the molecules must be contorted (deformed, or bent) into an unstable state called the transition state. The transition state is a high-energy state, and some amount of energy – the activation energy – must be added in order for the molecule reach it. Because the transition state is unstable, reactant molecules don’t stay there long, but quickly proceed to the next step of the chemical reaction.The activated complex is the highest energy of the transition state of the reaction.
Q12.5.5
Describe how graphical methods can be used to determine the activation energy of a reaction from a series of data that includes the rate of reaction at varying temperatures.
- Solution
-
This method is based on the Arrhenius equation which can be used to show the effect of a change of temperature on the rate constant, and therefore on the rate of reaction.
The rate constant is different from reaction rat in that the reaction rate is the measure of how fast or slow a chemical reaction takes place while a rate constant is a constant that shows the relationship between the reaction rate and the concentrations of the reactants or products.
For example, for the reaction \(A + B \rightarrow C\), the rate law would be:
\(rate = k[A]^a[B]^b\)
k = rate constant
[A] = concentration of reactant A
a = order of reaction with respect to A
[B] = concentration of reactant B
b = order of reaction with respect to B
However, the rate constant remains constant only if you are changing the concentration of the reactants. If you change the temperature or the catalyst of the reaction, the rate constant will change and this is demonstrated by the Arrhenius equation:
\(k = Ae^\frac{-E_a}{RT}\)
\(ln \left(\frac{k_1}{k_2}\right) = \left(\frac{-E_a}{R}\right)\left(\frac{1}{T_1} - \frac{1}{T_2}\right)\)
k = rate constant
A = frequency factor
\(E_a\) = activation energy
e = exponential function, \(e^x\)
R = gas constant
T = temperature (K)

In other words, the activation energy of a reaction, \(E_a\), from a series of data that includes the rate of reaction, k, at varying temperatures can be determined by graphing it on a plot of \(\ln k\) versus \(\frac{1}{T}\). You can then use the slope of the graph you have plotted to solve for \(E_a\) by setting the slope equal to \(\frac{-E_a}{R}\).
Q12.5.6
How does an increase in temperature affect rate of reaction? Explain this effect in terms of the collision theory of the reaction rate.
S12.5.6
Collision theory states that the rates of chemical reactions depend on the fraction of molecules with the correct orientation, fraction of collisions with required energy, and the collision frequency. Because the fraction of collisions with required energy is a function of temperature, as temperature increases, the fraction of collisions with required energy also increases. The kinetic energy of reactants also increases with temperature which means molecules will collide more often increasing collisions frequency. With increased fraction of collisions with required energy and collisions frequency, the rate of chemical reaction increases. We see mathematically, from the Arrhenius equation, that temperature and the rate constant are related.
\[k=Ae^{\frac {E_a}{RT}}\]
where k is the rate constant, A is a specific constant, R is 8.3145 J/K, Ea is the reaction-specific activation energy in J, and T is temperature in K. We see from the equation that k is very sensitive to changes in the temperature.
Q12.5.7
The rate of a certain reaction doubles for every 10 °C rise in temperature.
- How much faster does the reaction proceed at 45 °C than at 25 °C?
- How much faster does the reaction proceed at 95 °C than at 25 °C?
- Solution
-
By finding the difference in temperature, 45 °C - 25 °C, we get 20 °C. Since the rate of the reaction doubles every 10 °C increase in temperature and the rate of the reaction experienced a 20 °C increase in temperature, we see that the reaction rate doubled twice (22 = 4). As a result, the reaction proceeds four times faster.
Following the same process as in part a, we get the difference in temperature to be 70 °C. Since the rate of the reaction doubles every 10 °C increase in temperature and the system experienced a 70 °C change, we see that the reaction doubled seven times (27 = 128). We can see the reaction proceeds 128 times faster.
(a) 4-times faster (b) 128-times faster
Q12.5.8
In an experiment, a sample of NaClO3 was 90% decomposed in 48 min. Approximately how long would this decomposition have taken if the sample had been heated 20 °C higher?
S12.5.8
First off, it is important to recognize that this decomposition reaction is a first-order reaction, which can be written as follows: \(\mathrm2NaClO_3\to2NaCl + 3O_2\)
Understanding this, it is important to be able to then be able to recognize which equation would be most useful given the initial conditions presented by the question. Since we are dealing with time, percentage of material left, and temperature, the only viable equation that could relate all of this would be the Arrhenius Equation, which is written as follows: \(\mathrm \ln(\frac{k_2}{k_1}) = \frac {Ea}{R}({\frac1{t_1}}-{\frac{1}{t_{2}}})\)
However, this problem does not give us enough information such as what the activation energy is or the initial temperature in order to mathematically solve this problem. Additionally, the problem tells us to approximate how long the decomposition would take, which means we are asked to answer this question conceptually based on our knowledge of thermodynamics and reaction rates. As a general rule of thumb, we know that for every 10˚C rise in temperature the rate of reaction doubles. Since the question tells us that there is a 20˚C rise in temperature we can deduce that the reaction rate doubles twice, as per the general rule mentioned before. This means the overall reaction rate for this decomposition would quadruple, or would be 4 times faster than the reaction rate at the initial temperature.
We can gut check this answer by recalling how an increase in the average kinetic energy (temperature) decreases the time it takes for the reaction to take place and increase the reaction rate. Thus, if we increase the temperature we should have a faster reaction rate.
Q12.5.9
The rate constant at 325 °C for the decomposition reaction \(\ce{C4H8⟶2C2H4}\) is 6.1 × 10−8 s−1, and the activation energy is 261 kJ per mole of C4H8. Determine the frequency factor for the reaction.
- Solution
-
S12.5.9
Using the Arrhenius equation allows me to find the frequency factor, A.
k=Ae-Ea/RT
k, Ea, R, and T are all known values. k, Ea, and T are given in the problem as 6.1x10-8, 261 kJ, and 598 K, respectively.
So, plugging them into the equation gives:
6.1x10-8 s-1=Ae(-261000 J)/(8.3145 J/mol)(598 K)
Take e(-261000 J)/(8.3145 J/mol)(598) and get 1.59 x 10-23. Divide k, 6.1 x 10-8, by 1.59 x 10-23 and get A=3.9 x 1015s-1
-
A12.5.9
\(\mathrm{3.9×10^{15}\:s^{−1}}\)
Q12.5.10
The rate constant for the decomposition of acetaldehyde (CH3CHO), to methane (CH4), and carbon monoxide (CO), in the gas phase is 1.1 × 10−2 L/mol/s at 703 K and 4.95 L/mol/s at 865 K. Determine the activation energy for this decomposition.
S12.5.10
The equation for relating the rate constant and activation energy of a reaction is the Arrhenius equation:
\[k = Ae^ {-\frac{E_a}{RT}}\]
When given two rate constants at two different temperatures but for the same reaction, the Arrhenius equation can be rewritten as:
\[ln (\frac{k_2}{k_1}) = \frac{E_a}{R} (\frac{1}{T_1} - \frac{1}{T_2})\]
In this problem, all the variables are given except for the Ea (activation energy).
k1 = 1.1 × 10−2 L/mol/s
T1 = 703 K
k2 = 4.95 L/mol/s
T2 = 865 K
R = 8.314 J/(mol K) (Ideal Gas Constant)
Now plug in all these values into the equation, and solve for Ea.
\[ln (\frac{4.95\frac{L}{mol×s}}{1.1 × 10^{-2}\frac{L}{mol×s}}) = \frac{E_a}{8.314 × 10^{-3}\frac{kJ}{mol×K}} (\frac{1}{703} - \frac{1}{865})\]
Ea = 190 kJ (2 sig figs)
Q12.5.11
An elevated level of the enzyme alkaline phosphatase (ALP) in the serum is an indication of possible liver or bone disorder. The level of serum ALP is so low that it is very difficult to measure directly. However, ALP catalyzes a number of reactions, and its relative concentration can be determined by measuring the rate of one of these reactions under controlled conditions. One such reaction is the conversion of p-nitrophenyl phosphate (PNPP) to p-nitrophenoxide ion (PNP) and phosphate ion. Control of temperature during the test is very important; the rate of the reaction increases 1.47 times if the temperature changes from 30 °C to 37 °C. What is the activation energy for the ALP–catalyzed conversion of PNPP to PNP and phosphate?
- Solution
-
43.0 kJ/mol
Q12.5.12
In terms of collision theory, to which of the following is the rate of a chemical reaction proportional?
- the change in free energy per second
- the change in temperature per second
- the number of collisions per second
- the number of product molecules
Q12.5.13
Hydrogen iodide, HI, decomposes in the gas phase to produce hydrogen, H2, and iodine, I2. The value of the rate constant, k, for the reaction was measured at several different temperatures and the data are shown here:
| Temperature (K) | k (M−1 s−1) |
|---|---|
| 555 | 6.23 × 10−7 |
| 575 | 2.42 × 10−6 |
| 645 | 1.44 × 10−4 |
| 700 | 2.01 × 10−3 |
What is the value of the activation energy (in kJ/mol) for this reaction?
- Solution
-
177 kJ/mol
Q12.5.14
The element Co exists in two oxidation states, Co(II) and Co(III), and the ions form many complexes. The rate at which one of the complexes of Co(III) was reduced by Fe(II) in water was measured. Determine the activation energy of the reaction from the following data:
| T (K) | k (s−1) |
|---|---|
| 293 | 0.054 |
| 298 | 0.100 |
Q12.5.15
The hydrolysis of the sugar sucrose to the sugars glucose and fructose,
\[\ce{C12H22O11 + H2O ⟶ C6H12O6 + C6H12O6}\nonumber \]
follows a first-order rate equation for the disappearance of sucrose: Rate = k[C12H22O11] (The products of the reaction, glucose and fructose, have the same molecular formulas but differ in the arrangement of the atoms in their molecules.)
- In neutral solution, k = 2.1 × 10−11 s−1 at 27 °C and 8.5 × 10−11 s−1 at 37 °C. Determine the activation energy, the frequency factor, and the rate constant for this equation at 47 °C (assuming the kinetics remain consistent with the Arrhenius equation at this temperature).
- When a solution of sucrose with an initial concentration of 0.150 M reaches equilibrium, the concentration of sucrose is 1.65 × 10−7 M. How long will it take the solution to reach equilibrium at 27 °C in the absence of a catalyst? Because the concentration of sucrose at equilibrium is so low, assume that the reaction is irreversible.
- Why does assuming that the reaction is irreversible simplify the calculation in part (b)?
- Solution
-
Ea = 108 kJ
A = 2.0 × 108 s−1
k = 3.2 × 10−10 s−1
(b) 1.81 × 108 h or 7.6 × 106 day. (c) Assuming that the reaction is irreversible simplifies the calculation because we do not have to account for any reactant that, having been converted to product, returns to the original state.
Q12.5.16
Use the PhET Reactions & Rates interactive simulation to simulate a system. On the “Single collision” tab of the simulation applet, enable the “Energy view” by clicking the “+” icon. Select the first \(A+BC⟶AB+C\) reaction (A is yellow, B is purple, and C is navy blue). Using the “straight shot” default option, try launching the A atom with varying amounts of energy. What changes when the Total Energy line at launch is below the transition state of the Potential Energy line? Why? What happens when it is above the transition state? Why?
Q12.5.17
Use the PhET Reactions & Rates interactive simulation to simulate a system. On the “Single collision” tab of the simulation applet, enable the “Energy view” by clicking the “+” icon. Select the first \(A+BC⟶AB+C\) reaction (A is yellow, B is purple, and C is navy blue). Using the “angled shot” option, try launching the A atom with varying angles, but with more Total energy than the transition state. What happens when the A atom hits the BC molecule from different directions? Why?
- Solution
-
The A atom has enough energy to react with BC; however, the different angles at which it bounces off of BC without reacting indicate that the orientation of the molecule is an important part of the reaction kinetics and determines whether a reaction will occur.
12.6: Reaction Mechanisms
Q12.6.1
Why are elementary reactions involving three or more reactants very uncommon?
Q12.6.2
In general, can we predict the effect of doubling the concentration of A on the rate of the overall reaction \(A+B⟶C\) ? Can we predict the effect if the reaction is known to be an elementary reaction?
- Solution
-
Add texts here. Do not delete this text first.
No. In general, for the overall reaction, we cannot predict the effect of changing the concentration without knowing the rate equation. Yes. If the reaction is an elementary reaction, then doubling the concentration of A doubles the rate.
Q12.6.3
Phosgene, COCl2, one of the poison gases used during World War I, is formed from chlorine and carbon monoxide. The mechanism is thought to proceed by:
| step 1: | Cl + CO → COCl |
| step 2: | COCl + Cl2→ COCl2 + Cl |
- Write the overall reaction equation.
- Identify any reaction intermediates.
- Identify any intermediates.
Q12.6.4
Define these terms:
- unimolecular reaction
- bimolecular reaction
- elementary reaction
- overall reaction
Q12.6.5
What is the rate equation for the elementary termolecular reaction \(A+2B⟶\ce{products}\)? For \(3A⟶\ce{products}\)?
- Solution
-
Add texts here. Do not delete this text first.
We are given that both of these reactions are elementary termolecular. The molecularity of a reaction refers to the number of reactant particles that react together with the proper and energy and orientation. Termolecular reactions have three atoms to collide simultaneously. As it is termolecular, and there are no additional reactants aside from the three given in each reaction, there are no intermediate reactions. The rate law for elementary reactions is determined by the stoichiometry of the reaction without needed experimental data.
The basic rate form for the elementary step is what follows:
\(rate= {k} \cdot {reactant \ 1}^{i} \cdot {reactant \ 2}^{ii} \cdot ... \) Where i and ii are the stochiometric coefficient from reactant 1 and 2 respectively.
For: \(3A \rightarrow products \)
\({k} \cdot {A}^3 = rate\)
For: \(A + 2B \rightarrow products \)
\({k} \cdot {[A]} \cdot {[B]}^2 = rate\)
Note that the order of these reactions are both three.
- Answer
-
Add texts here. Do not delete this text first.
Rate = k[A][B]2; Rate = k[A]3
Q12.6.6
Given the following reactions and the corresponding rate laws, in which of the reactions might the elementary reaction and the overall reaction be the same?
(a) \(\ce{Cl2 + CO ⟶ Cl2CO}\)
\(\ce{rate}=k\ce{[Cl2]^{3/2}[CO]}\)
(b) \(\ce{PCl3 + Cl2 ⟶ PCl5}\)
\(\ce{rate}=k\ce{[PCl3][Cl2]}\)
(c) \(\ce{2NO + H2 ⟶ N2 + H2O}\)
\(\ce{rate}=k\ce{[NO][H2]}\)
(d) \(\ce{2NO + O2 ⟶ 2NO2}\)
\(\ce{rate}=k\ce{[NO]^2[O2]}\)
(e) \(\ce{NO + O3 ⟶ NO2 + O2}\)
\(\ce{rate}=k\ce{[NO][O3]}\)
- Solution
-
Add texts here. Do not delete this text first.
An elementary reaction is a chemical reaction in which the reactants directly form products in a single step. In another words, the rate law for the overall reaction is same as experimentally found rate law. Out of 5 options, option (b),(d), and (e) are such reactions
Q12.6.7
Write the rate equation for each of the following elementary reactions:
- \(\ce{O3 \xrightarrow{sunlight} O2 + O}\)
- \(\ce{O3 + Cl ⟶ O2 + ClO}\)
- \(\ce{ClO + O⟶ Cl + O2}\)
- \(\ce{O3 + NO ⟶ NO2 + O2}\)
- \(\ce{NO2 + O ⟶ NO + O2}\)
- Solution
-
Add texts here. Do not delete this text first.
Rate equations are dependent on the reactants and not the products.
The rate law of a reaction can be found using a rate constant (which is found experimentally), and the initial concentrations of reactants.
A general solution for the equation
\(aA + bB \rightarrow cC + dD\)
is \(rate = k[A]^{m}[B]^{n}\) where m and n are reaction orders.
However, reaction orders are found experimentally, and since we do not have experimental data for these reactions, we can disregard that part of the equation.
To find the rate laws, all we have to do is plug the reactants into the rate formula. This is only due to the case that these are elementary reactions. Further reading on elementary reactions can be found on Libre Texts.
a. O3 ⟶ O2 + O
To write this reaction's rate equation, only focus on the reactant(s) and its/their concentration and multiplying that by a rate constant, "k".
Rate = k[O3]
b. O3 + Cl ⟶ O2 + ClO
To write this reaction's rate equation, only focus on the reactant(s) and its/their concentration and multiplying that by a rate constant, "k".
Rate = k[O3][Cl]
c. ClO + O ⟶ Cl + O2
To write this reaction's rate equation, only focus on the reactant(s) and its/their concentration and multiplying that by a rate constant, "k".
Rate = k[ClO][O]
d. O3 + NO ⟶ NO2 + O2
To write this reaction's rate equation, only focus on the reactant(s) and its/their concentration and multiplying that by a rate constant, "k".
Rate = k[O3][NO]
e. NO2 + O ⟶ NO + O2
To write this reaction's rate equation, only focus on the reactant(s) and its/their concentration and multiplying that by a rate constant, "k".
Rate = k[NO2][O]
- Answer
-
Add texts here. Do not delete this text first.
(a) Rate1 = k[O3]; (b) Rate2 = k[O3][Cl]; (c) Rate3 = k[ClO][O]; (d) Rate2 = k[O3][NO]; (e) Rate3 = k[NO2][O]
Q12.6.8
Nitrogen(II) oxide, NO, reacts with hydrogen, H2, according to the following equation:
\[\ce{2NO + 2H2 ⟶ N2 + 2H2O}\nonumber \]
What would the rate law be if the mechanism for this reaction were:
\[\ce{2NO + H2 ⟶ N2 + H2O2\:(slow)}\nonumber \]
\[\ce{H2O2 + H2 ⟶ 2H2O\:(fast)}\nonumber \]
The rate law of the mechanism is determined by the slow step of the reaction. Since the slow step is an elementary step, the rate law can be drawn from the coefficients of the chemical equation. So therefore, the rate law is as follows: rate=k[NO]2[H2]. Since both NO and H2 are reactants in the overall reaction (therefore are not intermediates in the reaction), no further steps have to be done to determine the rate law.
Q12.6.9
Consider the reaction
CH4 + Cl2 → CH3Cl + HCl (occurs under light)
The mechanism is a chain reaction involving Cl atoms and CH3 radicals. Which of the following steps does not terminate this chain reaction?
- CH3 + Cl → CH3CI
- CH3 + HCl → CH4 + Cl
- CH3 + CH3 → C2H2
- Cl + Cl → Cl2
- Solution
-
Add texts here. Do not delete this text first.
Chain reactions involve reactions that create products necessary for more reactions to occur. In this case, a reaction step will continue the chain reaction if a radical is generated. Radicals are highly reactive particles, so more reactions in the chain will take place as long as they are present. The chlorine is considered a free radical as it has an unpaired electron; for this reason it is very reactive and propagates a chain reaction. It does so by taking an electron from a stable molecule and making that molecule reactive, and that molecule goes on to react with stable species, and in that manner a long series of "chain" reactions are initiated. A chlorine radical will continue the chain by completing the following reaction:
\({Cl \cdot}+{CH_4} \rightarrow {CH_3 \cdot}+{HCl} \)
The \({CH_3}\) generated by this reaction can then react with other species, continuing to propagate the chain reaction.
Option 1 is incorrect because the only species it produces is \({CH_3Cl}\), a product in the overall reaction that is unreactive. This terminates the chain reaction because it fails to produce any \(Cl\) or \(CH_3\) radicals that are necessary for further propagating the overall reaction.
Option 2 is the correct answer because it produces a \(Cl\) radical. This \(Cl\) radical can continue the chain by colliding with \(CH_4\) molecules.
Option 3 is incorrect because it fails to produce a radical capable of continuing the chain.
Option 4 is incorrect because it produces \(Cl_2\), a molecule that does not react unless additional light is supplied. Therefore, this step breaks the chain.
- Answer
-
Add texts here. Do not delete this text first.
Answer: Option 2: \({CH_3}+{HCl} \rightarrow {CH_4}+{Cl}\)
Q12.6.10
Experiments were conducted to study the rate of the reaction represented by this equation.
\[\ce{2NO}(g)+\ce{2H2}(g)⟶\ce{N2}(g)+\ce{2H2O}(g)\nonumber \]
Initial concentrations and rates of reaction are given here.
| Experiment | Initial Concentration [NO] (mol/L) | Initial Concentration, [H2] (mol/L) | Initial Rate of Formation of N2 (mol/L min) |
|---|---|---|---|
| 1 | 0.0060 | 0.0010 | 1.8 × 10−4 |
| 2 | 0.0060 | 0.0020 | 3.6 × 10−4 |
| 3 | 0.0010 | 0.0060 | 0.30 × 10−4 |
| 4 | 0.0020 | 0.0060 | 1.2 × 10−4 |
Consider the following questions:
- Determine the order for each of the reactants, NO and H2, from the data given and show your reasoning.
- Write the overall rate law for the reaction.
- Calculate the value of the rate constant, k, for the reaction. Include units.
- For experiment 2, calculate the concentration of NO remaining when exactly one-half of the original amount of H2 had been consumed.
- The following sequence of elementary steps is a proposed mechanism for the reaction.
Step 1: \(\ce{NO + NO ⇌ N2O2}\)
Step 2: \(\ce{N2O2 + H2 ⇌ H2O + N2O}\)
Step 3: \(\ce{N2O + H2 ⇌ N2 + H2O}\)
Based on the data presented, which of these is the rate determining step? Show that the mechanism is consistent with the observed rate law for the reaction and the overall stoichiometry of the reaction.
S12.6.10
1. i) Find the order for [NO] by using experiment 3 and 4 where [H2] is constant
Notice that [NO] doubles from experiment 3 to 4 and the rate quadruples. So the order for [NO] is 2
ii) Find the order for [H2] by using experiment 1 and 2 where [NO] is constant
Notice that [H2] doubles from experiment 1 to 2 and the rate doubles as well. So the order for [H2] is 1
2. Put in the order for each product as the exponents for the corresponding reactant.
\(rate = k [NO]^2 [H_2]\)
3. Put in the concentrations and the rate from one of the experiments into the rate law and solve for k. (Here, experiement 1 is used but any of them will work)
\(rate = k [NO]^2 [H_2]\) \(.00018 = k [.006]^2 [.001]\) \(k = 5000 M^{-2}s^{-1}\)
4. Plug in values for experiment 2 into the rate law equation and solve for the concentration of NO
\(.00036=5000[NO]^2[.001]\) \([NO]^2= 7.2 x 10^{-5}\) \([NO] = .0085 M\)
5. Write the rate laws for each step and then see which matches the rate law we found in question 2. The rate determining step (the slow step) is the one that gives the rate for the overall reaction. Because of this, only those concentrations will influence the overall reaction, contrary to what we would believe if we just looked at the overall reaction.
Step 1: \(NO + NO \rightleftharpoons N_2O_2\)
\(rate =k_1[NO]^2\) This rate law is not the same as the one we calculate in question 2 so this can not be the rate determining step
Step 2: \(N_2O_2+H_2 \rightleftharpoons N_2O + N_2O\)
\(rate = k_2[N_2O_2][H_2]\)
Since \(N_2O_2\) is an intermediate you must replace it in the rate law equation. Intermediates can not be in the rate law because they do not appear in the overall reaction. Here you can take the reverse of equation 1 (k-1) and substitute the other side (the reactants of equation 1) for the intermediate in the rate law equation.
\[rate_1 = rate_{-1}\nonumber \]
\[k_1[NO]^2 = k_{-1}[N_2O_2]\nonumber \]
\[[N_2O_2] = \frac{k_1[NO]^2}{k_{-1}}\nonumber \]
\(rate= \frac{k_2k_{1}[NO]^2[H_2]}{k_{-1}}\)
Overall: \(rate={k[NO]^2[H_2]}\) This is the same so it is the rate determining step.
So \(N_2O_2+H_2 \rightleftharpoons N_2O + N_2O\) is the rate determining step step.
- Answer
-
Add texts here. Do not delete this text first.
(a) NO: 2
\(\ce {H2}\) : 1
(b) Rate = k [NO]2[H2];
(c) k = 5.0 × 103 mol−2 L−2 min−1;
(d) 0.0050 mol/L;
(e) Step II is the rate-determining step.
Q12.6.11
The reaction of CO with Cl2 gives phosgene (COCl2), a nerve gas that was used in World War I. Use the mechanism shown here to complete the following exercises:
- \(\ce{Cl2}(g)⇌\ce{2Cl}(g)\) (fast, k1 represents the forward rate constant, k−1 the reverse rate constant)
- \(\ce{CO}(g)+\ce{Cl}(g)⟶\ce{COCl}(g)\) (slow, k2 the rate constant)
- \(\ce{COCl}(g)+\ce{Cl}(g)⟶\ce{COCl2}(g)\) (fast, k3 the rate constant)
- Write the overall reaction.
- Identify all intermediates.
- Write the rate law for each elementary reaction.
- Write the overall rate law expression.
- Solution
-
Add texts here. Do not delete this text first.
1. To write the overall reaction you have to identify the intermediates and leave them out. The easiest way to do this is to write out all the products and reactants and cross out anything that is on both sides.
Cl2(g) + CO(g) + 2Cl(g) +COCl(g) ⇒ 2Cl(g) + COCl(g) + COCl2(g)
In this you will cross out the 2Cl(g) molecules and the COCl(g). What is left after that is the overall reaction.
Cl2(g) + CO(g) ⇒ + COCl2(g)
2. For part two you will just list the intermediates that you crossed out.
Cl and COCl are intermediates
3. Each rate law will be the rate equal to the rate constant times the concentrations of the reactants
reaction 1
(forward) rate=k1[Cl2] ( reverse) rate=k-1[Cl]
reaction 2
rate=k2[CO][Cl]
Reaction 3
rate=k3[COCl][Cl]
4. The overall rate law is based off the slowest step (step #2), since it is the rate determining step, but Cl is present in that rate law so we have to replace it with an equivalent that does not contain an intermediate. To do this you use the equilibrium since the rates are the same you can set up the rate laws of the forward and reverse equal to each other.
k1[Cl2] = k-1[Cl]
[Cl]= k1[Cl2]/k-1
rate=k2[CO]k1[Cl2]/k-1
rate=k°[CO][Cl2]
Steps to replacing and intermediate
- Set the forward and reverse reaction equal to each other using separate constants
- Solve for the intermediate using algebra
- Plug into the rate determining formula
- All the k's will be condensed into a K prime constant
12.7: Catalysis
Q12.7.1
Account for the increase in reaction rate brought about by a catalyst.
Q12.7.2
Compare the functions of homogeneous and heterogeneous catalysts.
Q12.7.3
Consider this scenario and answer the following questions: Chlorine atoms resulting from decomposition of chlorofluoromethanes, such as CCl2F2, catalyze the decomposition of ozone in the atmosphere. One simplified mechanism for the decomposition is: \[\ce{O3 \xrightarrow{sunlight} O2 + O}\\ \ce{O3 + Cl ⟶ O2 + ClO}\\ \ce{ClO + O ⟶ Cl + O2}\nonumber \]
- Explain why chlorine atoms are catalysts in the gas-phase transformation: \[\ce{2O3⟶3O2}\nonumber \]
- Nitric oxide is also involved in the decomposition of ozone by the mechanism: \[\ce{O3 \xrightarrow{sunlight} O2 + O\\ O3 + NO ⟶ NO2 + O2\\ NO2 + O ⟶ NO + O2}\nonumber \]
Is NO a catalyst for the decomposition? Explain your answer.
Q12.7.4
For each of the following pairs of reaction diagrams, identify which of the pair is catalyzed:
(a)
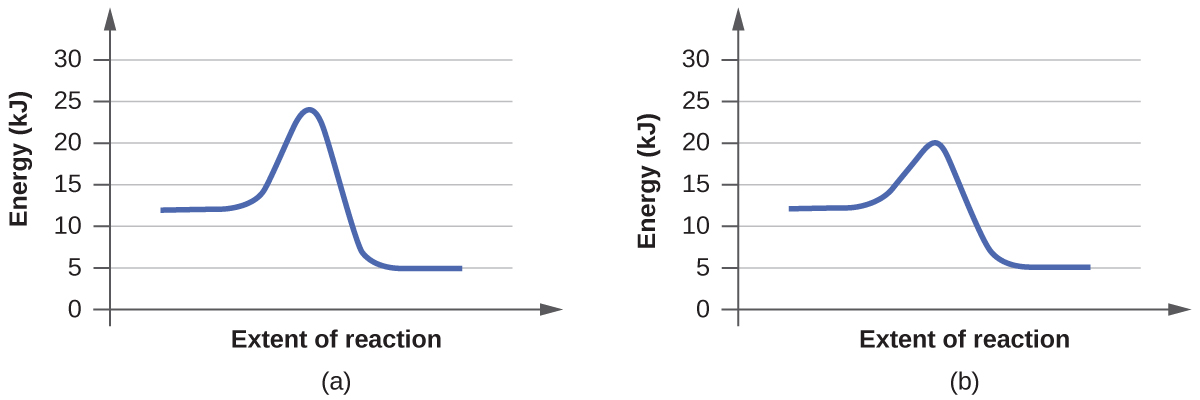
Q12.7.5
For each of the following pairs of reaction diagrams, identify which of the pairs is catalyzed:
(a)
(b)
Q12.7.6
For each of the following reaction diagrams, estimate the activation energy (Ea) of the reaction:
(a)
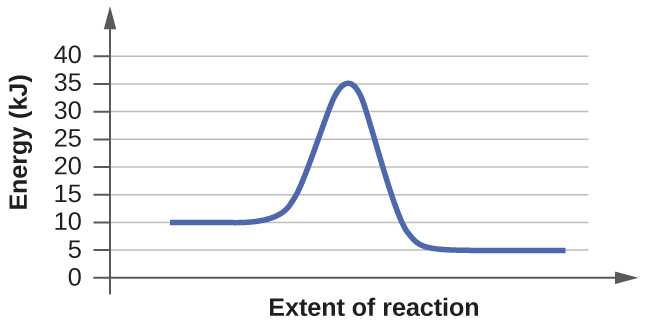
(b)
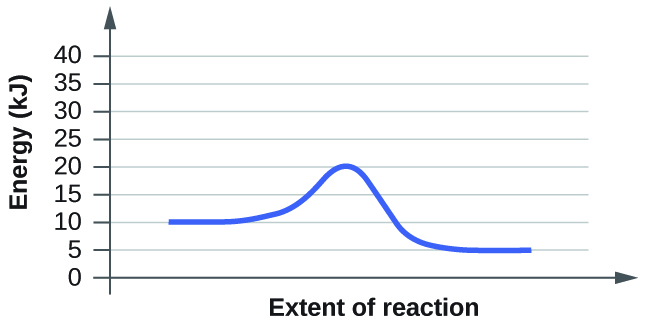
Q12.7.7
For each of the following reaction diagrams, estimate the activation energy (Ea) of the reaction:
(a)
(b)
Q12.7.8
- Based on the diagrams in Question Q12.7.6, which of the reactions has the fastest rate? Which has the slowest rate?
- Based on the diagrams in Question Q12.7.7, which of the reactions has the fastest rate? Which has the slowest rate?



![{\displaystyle t_{\frac {1}{2}}={\frac {1}{k{\ce {[A]0}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b25f9b5e7675b3e3f9027241a74ec2d751810c43)