4.2: Writing and Balancing Chemical Equations
- Page ID
- 38156
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Derive chemical equations from narrative descriptions of chemical reactions.
- Write and balance chemical equations in molecular, total ionic, and net ionic formats.
The preceding chapter introduced the use of element symbols to represent individual atoms. When atoms gain or lose electrons to yield ions, or combine with other atoms to form molecules, their symbols are modified or combined to generate chemical formulas that appropriately represent these species. Extending this symbolism to represent both the identities and the relative quantities of substances undergoing a chemical (or physical) change involves writing and balancing a chemical equation. Consider as an example the reaction between one methane molecule (CH4) and two diatomic oxygen molecules (O2) to produce one carbon dioxide molecule (CO2) and two water molecules (H2O). The chemical equation representing this process is provided in the upper half of Figure \(\PageIndex{1}\), with space-filling molecular models shown in the lower half of the figure.
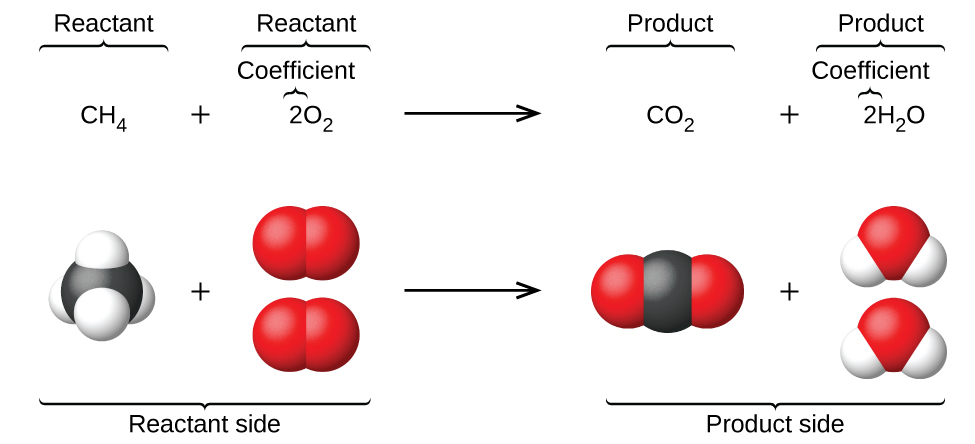
This example illustrates the fundamental aspects of any chemical equation:
- The substances undergoing reaction are called reactants, and their formulas are placed on the left side of the equation.
- The substances generated by the reaction are called products, and their formulas are placed on the right sight of the equation.
- Plus signs (+) separate individual reactant and product formulas, and an arrow (⟶) separates the reactant and product (left and right) sides of the equation.
- The relative numbers of reactant and product species are represented by coefficients (numbers placed immediately to the left of each formula). A coefficient of 1 is typically omitted.
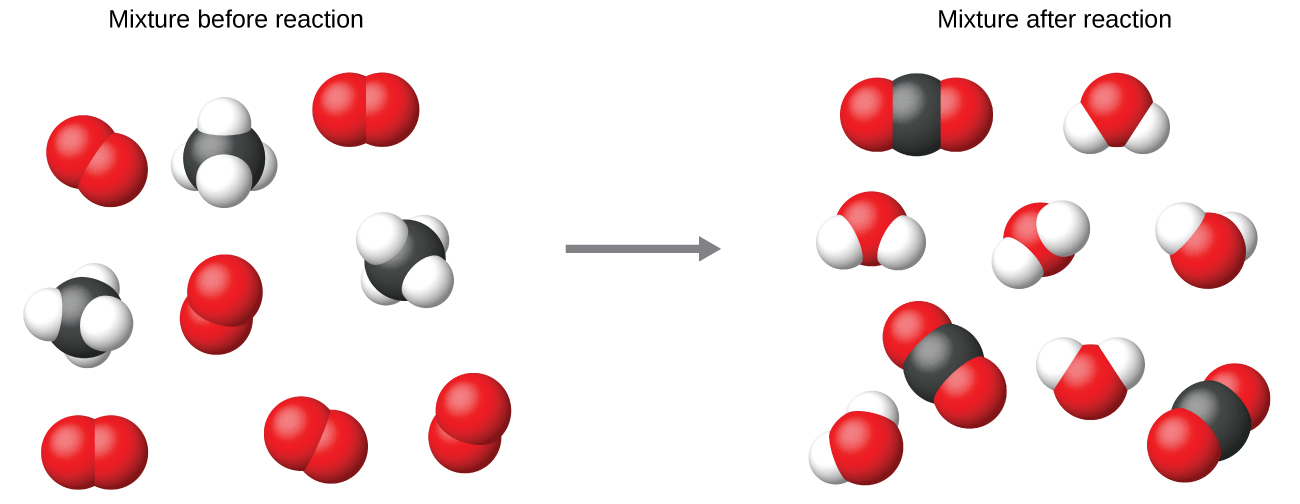
It is common practice to use the smallest possible whole-number coefficients in a chemical equation, as is done in this example. Realize, however, that these coefficients represent the relative numbers of reactants and products, and, therefore, they may be correctly interpreted as ratios. Methane and oxygen react to yield carbon dioxide and water in a 1:2:1:2 ratio. This ratio is satisfied if the numbers of these molecules are, respectively, 1-2-1-2, or 2-4-2-4, or 3-6-3-6, and so on (Figure \(\PageIndex{2}\)). Likewise, these coefficients may be interpreted with regard to any amount (number) unit, and so this equation may be correctly read in many ways, including:
- One methane molecule and two oxygen molecules react to yield one carbon dioxide molecule and two water molecules.
- One dozen methane molecules and two dozen oxygen molecules react to yield one dozen carbon dioxide molecules and two dozen water molecules.
- One mole of methane molecules and 2 moles of oxygen molecules react to yield 1 mole of carbon dioxide molecules and 2 moles of water molecules.
Balancing Equations
When a chemical equation is balanced it means that equal numbers of atoms for each element involved in the reaction are represented on the reactant and product sides. This is a requirement the equation must satisfy to be consistent with the law of conservation of matter. It may be confirmed by simply summing the numbers of atoms on either side of the arrow and comparing these sums to ensure they are equal. Note that the number of atoms for a given element is calculated by multiplying the coefficient of any formula containing that element by the element’s subscript in the formula. If an element appears in more than one formula on a given side of the equation, the number of atoms represented in each must be computed and then added together. For example, both product species in the example reaction, \(\ce{CO2}\) and \(\ce{H2O}\), contain the element oxygen, and so the number of oxygen atoms on the product side of the equation is
\[\left(1\: \cancel{\ce{CO_2} \: \text{molecule}} \times \dfrac{2\: \ce{O} \: \text{atoms}}{ \cancel{\ce{CO_2} \: \text{molecule}}}\right) + \left( \cancel{ \ce{2H_2O} \: \text{molecule} }\times \dfrac{1\: \ce{O}\: \text{atom}}{\cancel{ \ce{H_2O} \: \text{molecule}}}\right)=4\: \ce{O} \: \text{atoms} \nonumber \]
The equation for the reaction between methane and oxygen to yield carbon dioxide and water is confirmed to be balanced per this approach, as shown here:
\[\ce{CH4 +2O2\rightarrow CO2 +2H2O} \nonumber \]
| Element | Reactants | Products | Balanced? |
|---|---|---|---|
| C | 1 × 1 = 1 | 1 × 1 = 1 | 1 = 1, yes |
| H | 4 × 1 = 4 | 2 × 2 = 4 | 4 = 4, yes |
| O | 2 × 2 = 4 | (1 × 2) + (2 × 1) = 4 | 4 = 4, yes |
A balanced chemical equation often may be derived from a qualitative description of some chemical reaction by a fairly simple approach known as balancing by inspection. Consider as an example the decomposition of water to yield molecular hydrogen and oxygen. This process is represented qualitatively by an unbalanced chemical equation:
\[\ce{H2O \rightarrow H2 + O2} \tag{unbalanced} \]
Comparing the number of H and O atoms on either side of this equation confirms its imbalance:
| Element | Reactants | Products | Balanced? |
|---|---|---|---|
| H | 1 × 2 = 2 | 1 × 2 = 2 | 2 = 2, yes |
| O | 1 × 1 = 1 | 1 × 2 = 2 | 1 ≠ 2, no |
The numbers of H atoms on the reactant and product sides of the equation are equal, but the numbers of O atoms are not. To achieve balance, the coefficients of the equation may be changed as needed. Keep in mind, of course, that the formula subscripts define, in part, the identity of the substance, and so these cannot be changed without altering the qualitative meaning of the equation. For example, changing the reactant formula from H2O to H2O2 would yield balance in the number of atoms, but doing so also changes the reactant’s identity (it’s now hydrogen peroxide and not water). The O atom balance may be achieved by changing the coefficient for H2O to 2.
\[\ce{2H2O \rightarrow H2 + O2} \tag{unbalanced} \]
| Element | Reactants | Products | Balanced? |
|---|---|---|---|
| H | 2 × 2 = 4 | 1 × 2 = 2 | 4 ≠ 2, no |
| O | 2 × 1 = 2 | 1 × 2 = 2 | 2 = 2, yes |
The H atom balance was upset by this change, but it is easily reestablished by changing the coefficient for the H2 product to 2.
\[\ce{2H_2O \rightarrow 2H2 + O2} \tag{balanced} \]
| Element | Reactants | Products | Balanced? |
|---|---|---|---|
| H | 2 × 2 = 4 | 2 × 2 = 2 | 4 = 4, yes |
| O | 2 × 1 = 2 | 1 × 2 = 2 | 2 = 2, yes |
These coefficients yield equal numbers of both H and O atoms on the reactant and product sides, and the balanced equation is, therefore:
\[\ce{2H_2O \rightarrow 2H_2 + O_2} \nonumber \]
Write a balanced equation for the reaction of molecular nitrogen (N2) and oxygen (O2) to form dinitrogen pentoxide.
Solution
First, write the unbalanced equation.
\[\ce{N_2 + O_2 \rightarrow N_2O_5} \tag{unbalanced} \]
Next, count the number of each type of atom present in the unbalanced equation.
| Element | Reactants | Products | Balanced? |
|---|---|---|---|
| N | 1 × 2 = 2 | 1 × 2 = 2 | 2 = 2, yes |
| O | 1 × 2 = 2 | 1 × 5 = 5 | 2 ≠ 5, no |
Though nitrogen is balanced, changes in coefficients are needed to balance the number of oxygen atoms. To balance the number of oxygen atoms, a reasonable first attempt would be to change the coefficients for the O2 and N2O5 to integers that will yield 10 O atoms (the least common multiple for the O atom subscripts in these two formulas).
\[\ce{N_2 + 5 O2 \rightarrow 2 N2O5} \tag{unbalanced} \]
| Element | Reactants | Products | Balanced? |
|---|---|---|---|
| N | 1 × 2 = 2 | 2 × 2 = 4 | 2 ≠ 4, no |
| O | 5 × 2 = 10 | 2 × 5 = 10 | 10 = 10, yes |
The N atom balance has been upset by this change; it is restored by changing the coefficient for the reactant N2 to 2.
\[\ce{2N_2 + 5O_2\rightarrow 2N_2O_5} \nonumber \]
| Element | Reactants | Products | Balanced? |
|---|---|---|---|
| N | 2 × 2 = 4 | 2 × 2 = 4 | 4 = 4, yes |
| O | 5 × 2 = 10 | 2 × 5 = 10 | 10 = 10, yes |
The numbers of N and O atoms on either side of the equation are now equal, and so the equation is balanced.
Write a balanced equation for the decomposition of ammonium nitrate to form molecular nitrogen, molecular oxygen, and water. (Hint: Balance oxygen last, since it is present in more than one molecule on the right side of the equation.)
- Answer
-
\[\ce{2NH4NO3 \rightarrow 2N2 + O2 + 4H2O} \nonumber \]
Balancing Reactions Which Contain Polyatomics: Balancing Reactions Which Contain Polyatomics(opens in new window) [youtu.be]
It is sometimes convenient to use fractions instead of integers as intermediate coefficients in the process of balancing a chemical equation. When balance is achieved, all the equation’s coefficients may then be multiplied by a whole number to convert the fractional coefficients to integers without upsetting the atom balance. For example, consider the reaction of ethane (C2H6) with oxygen to yield H2O and CO2, represented by the unbalanced equation:
\[\ce{C_2H_6 + O_2 \rightarrow H_2O + CO_2} \tag{unbalanced} \]
Following the usual inspection approach, one might first balance C and H atoms by changing the coefficients for the two product species, as shown:
\[\ce{C_2H_6 + O_2 \rightarrow 3H_2O + 2CO_2} \tag{unbalanced} \]
This results in seven O atoms on the product side of the equation, an odd number—no integer coefficient can be used with the O2 reactant to yield an odd number, so a fractional coefficient, \(\ce{7/2}\), is used instead to yield a provisional balanced equation:
\[\ce{C2H6 + 7/2 O2\rightarrow 3H2O + 2CO2} \nonumber \]
A conventional balanced equation with integer-only coefficients is derived by multiplying each coefficient by 2:
\[\ce{2C2H6 +7O2\rightarrow 6H2O + 4CO2} \nonumber \]
Finally with regard to balanced equations, recall that convention dictates use of the smallest whole-number coefficients. Although the equation for the reaction between molecular nitrogen and molecular hydrogen to produce ammonia is, indeed, balanced,
\[\ce{3N2 +9H2\rightarrow 6NH3} \nonumber \]
the coefficients are not the smallest possible integers representing the relative numbers of reactant and product molecules. Dividing each coefficient by the greatest common factor, 3, gives the preferred equation:
\[\ce{N2 + 3H2\rightarrow 2NH3} \nonumber \]
Use this interactive tutorial for additional practice balancing equations.
Additional Information in Chemical Equations
The physical states of reactants and products in chemical equations very often are indicated with a parenthetical abbreviation following the formulas. Common abbreviations include s for solids, l for liquids, g for gases, and aq for substances dissolved in water (aqueous solutions, as introduced in the preceding chapter). These notations are illustrated in the example equation here:
\[\ce{2Na (s) + 2H2O (l) \rightarrow 2NaOH (aq) + H2(g)} \nonumber \]
This equation represents the reaction that takes place when sodium metal is placed in water. The solid sodium reacts with liquid water to produce molecular hydrogen gas and the ionic compound sodium hydroxide (a solid in pure form, but readily dissolved in water).
Special conditions necessary for a reaction are sometimes designated by writing a word or symbol above or below the equation’s arrow. For example, a reaction carried out by heating may be indicated by the uppercase Greek letter delta (Δ) over the arrow.
\[\ce{CaCO3}(s)\xrightarrow{\:\Delta\:} \ce{CaO}(s)+\ce{CO2}(g) \nonumber \]
Other examples of these special conditions will be encountered in more depth in later chapters.
Equations for Ionic Reactions
Given the abundance of water on earth, it stands to reason that a great many chemical reactions take place in aqueous media. When ions are involved in these reactions, the chemical equations may be written with various levels of detail appropriate to their intended use. To illustrate this, consider a reaction between ionic compounds taking place in an aqueous solution. When aqueous solutions of \(\ce{CaCl2}\) and \(\ce{AgNO3}\) are mixed, a reaction takes place producing aqueous \(\ce{Ca(NO3)2}\) and solid \(\ce{AgCl}\):
\[\ce{CaCl2}(aq)+\ce{2AgNO3}(aq)\rightarrow \ce{Ca(NO3)2}(aq)+\ce{2AgCl}(s) \nonumber \]
This balanced equation, derived in the usual fashion, is called a molecular equation because it doesn’t explicitly represent the ionic species that are present in solution. When ionic compounds dissolve in water, they may dissociate into their constituent ions, which are subsequently dispersed homogenously throughout the resulting solution (a thorough discussion of this important process is provided in the chapter on solutions). Ionic compounds dissolved in water are, therefore, more realistically represented as dissociated ions, in this case:
\[\ce{CaCl2}(aq)\rightarrow \ce{Ca^2+}(aq)+\ce{2Cl-}(aq) \nonumber \]
\[\ce{2AgNO3}(aq)\rightarrow \ce{2Ag+}(aq)+\ce{2NO3-}(aq) \nonumber \]
\[\ce{Ca(NO3)2}(aq)\rightarrow \ce{Ca^2+}(aq)+\ce{2NO3-}(aq) \nonumber \]
Unlike these three ionic compounds, AgCl does not dissolve in water to a significant extent, as signified by its physical state notation, (s).
Explicitly representing all dissolved ions results in a complete ionic equation. In this particular case, the formulas for the dissolved ionic compounds are replaced by formulas for their dissociated ions:
\[\ce{Ca^2+}(aq)+\ce{2Cl-}(aq)+\ce{2Ag+}(aq)+\ce{2NO3-}(aq)\rightarrow \ce{Ca^2+}(aq)+\ce{2NO3-}(aq)+\ce{2AgCl}(s) \nonumber \]
Examining this equation shows that two chemical species are present in identical form on both sides of the arrow, \(\ce{Ca^{2+}(aq)}\) and \(\ce{NO3-}(aq)\). These spectator ions—ions whose presence is required to maintain charge neutrality—are neither chemically nor physically changed by the process, and so they may be eliminated from the equation to yield a more succinct representation called a net ionic equation:
\[\cancel{\ce{Ca^2+}(aq)}+\ce{2Cl-}(aq)+\ce{2Ag+}(aq)+\cancel{\ce{2NO3-}(aq)}\rightarrow \cancel{\ce{Ca^2+}(aq)}+\cancel{\ce{2NO3-}(aq)}+\ce{2AgCl}(s) \nonumber \]
\[\ce{2Cl-}(aq)+\ce{2Ag+}(aq)\rightarrow \ce{2AgCl}(s) \nonumber \]
Following the convention of using the smallest possible integers as coefficients, this equation is then written:
\[\ce{Cl-}(aq)+\ce{Ag+}(aq)\rightarrow \ce{AgCl}(s) \nonumber \]
This net ionic equation indicates that solid silver chloride may be produced from dissolved chloride and silver(I) ions, regardless of the source of these ions. These molecular and complete ionic equations provide additional information, namely, the ionic compounds used as sources of \(\ce{Cl^{−}}\) and \(\ce{Ag+}\).
When carbon dioxide is dissolved in an aqueous solution of sodium hydroxide, the mixture reacts to yield aqueous sodium carbonate and liquid water. Write balanced molecular, complete ionic, and net ionic equations for this process.
Solution
Begin by identifying formulas for the reactants and products and arranging them properly in chemical equation form:
\[\ce{CO2(aq) + NaOH(aq) \rightarrow Na2CO3(aq) + H2O(l)} \tag{unbalanced} \]
Balance is achieved easily in this case by changing the coefficient for NaOH to 2, resulting in the molecular equation for this reaction:
\[\ce{CO2(aq)+2NaOH(aq)\rightarrow Na2CO3(aq) + H2O}(l) \nonumber \]
The two dissolved ionic compounds, NaOH and Na2CO3, can be represented as dissociated ions to yield the complete ionic equation:
\[\ce{CO2 (aq) + 2Na+ (aq) + 2OH- (aq) \rightarrow 2Na+ (aq) + CO3^{2-} (aq) + H2O (l)} \nonumber \]
Finally, identify the spectator ion(s), in this case Na+(aq), and remove it from each side of the equation to generate the net ionic equation:
\[\begin{align*}
\ce{CO2}(aq)+\cancel{\ce{2Na+}(aq)}+\ce{2OH-}(aq)&\rightarrow \cancel{\ce{2Na+}(aq)}+\ce{CO3^2-}(aq)+\ce{H2O}(l)\\
\ce{CO2}(aq)+\ce{2OH-}(aq)&\rightarrow \ce{CO3^2-}(aq)+\ce{H2O}(l)
\end{align*} \nonumber \]
Diatomic chlorine and sodium hydroxide (lye) are commodity chemicals produced in large quantities, along with diatomic hydrogen, via the electrolysis of brine, according to the following unbalanced equation:
\[\ce{NaCl(aq) + H2O(l) ->[ electricity] NaOH(aq) + H2(g) + Cl2(g)} \nonumber \]
Write balanced molecular, complete ionic, and net ionic equations for this process.
- Answer
-
Balanced molecular equation: \[\ce{2NaCl(aq) + 2H2O(l) -> 2NaOH(aq) + H2(g) + Cl2(g)} \nonumber \]
Balanced ionic equation: \[\ce{2Na^{+}(aq) + 2Cl^{-}(aq) + 2H2O (l) -> 2Na^{+}(aq) + 2OH^{-}(aq) + H2(g) + Cl2(g)} \nonumber \]
Balanced net ionic equation: \[\ce{2Cl^{-}(aq) + 2H2O(l) -> 2OH^{-}(aq) + H2(g) + Cl2(g) } \nonumber \]
Key Concepts and Summary
Chemical equations are symbolic representations of chemical and physical changes. Formulas for the substances undergoing the change (reactants) and substances generated by the change (products) are separated by an arrow and preceded by integer coefficients indicating their relative numbers. Balanced equations are those whose coefficients result in equal numbers of atoms for each element in the reactants and products. Chemical reactions in aqueous solution that involve ionic reactants or products may be represented more realistically by complete ionic equations and, more succinctly, by net ionic equations.
Glossary
- balanced equation
- chemical equation with equal numbers of atoms for each element in the reactant and product
- chemical equation
- symbolic representation of a chemical reaction
- coefficient
- number placed in front of symbols or formulas in a chemical equation to indicate their relative amount
- complete ionic equation
- chemical equation in which all dissolved ionic reactants and products, including spectator ions, are explicitly represented by formulas for their dissociated ions
- molecular equation
- chemical equation in which all reactants and products are represented as neutral substances
- net ionic equation
- chemical equation in which only those dissolved ionic reactants and products that undergo a chemical or physical change are represented (excludes spectator ions)
- product
- substance formed by a chemical or physical change; shown on the right side of the arrow in a chemical equation
- reactant
- substance undergoing a chemical or physical change; shown on the left side of the arrow in a chemical equation
- spectator ion
- ion that does not undergo a chemical or physical change during a reaction, but its presence is required to maintain charge neutrality


