5.16: Electron Configurations
- Page ID
- 49337
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In order to examine the results of the wave theory of the electron for each element in the periodic table, we must recall the general rules that are necessary in order to predict electron configurations for all atoms of the elements. To review, these rules are as follows:
- 1 The Aufbauprinciple (building-up principle). The structure of an atom may be built up from that of the element preceding it in the periodic system by adding one proton (and an appropriate number of neutrons) to the nucleus and one extranuclear electron.
- 2 The order of filling orbitals. Each time an electron is added, it occupies the available subshell of lowest energy. The appropriate shell may be determined from a diagram such as Figure \(\PageIndex{1}\) a which arranges the subshells in order of increasing energy. Once a subshell becomes filled, the subshell of the next higher energy starts to fill.
- 3 The Pauli exclusion principle. No more than two electrons can occupy a single orbital. When two electrons occupy the same orbital, they must be of opposite spin (an electron pair).
- 4 Hund’s rule. When electrons are added to a subshell where more than one orbital of the same energy is available, their spins remain parallel and they occupy different orbitals. Electron pairing does not occur until it is required by lack of another empty orbital in the subshell.
The order in which the subshells are filled merits some discussion. As can be seen in Figure \(\PageIndex{1}\) a within a given shell the energies of the subshells increase in the order s < p < d <f.
When we discussed the boron atom, we saw that a p orbital is higher in energy than the s orbital in the same shell because the p orbital is more effectively screened from the nucleus. Similar reasoning explains why d orbitals are higher in energy than p orbitals but lower than f orbitals.
Not only are the energies of a given shell spread out in this way, but there is sometimes an overlap in energy between shells. As can be seen from Figure \(\PageIndex{1}\) a the subshell of highest energy in the third shell, namely, 3d, is above the subshell of lowest energy in the fourth shell, namely, 4s.
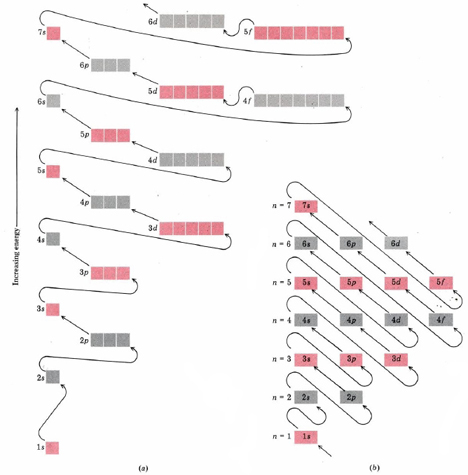
Similar overlaps occur among subshells of the fourth, fifth, sixth, and seventh shells. These cause exceptions to the expected order of filling subshells. The 6s orbital, for example, starts to fill before the 4f.
Although the order in which the subshells fill seems hopelessly complex at first sight, there is a very simple device available for remembering it.
This is shown in Figure \(\PageIndex{1}\) b. The rows in this table consist of all possible subshells within each shell. For example, the second row from the bottom contains 2s and 2p, the two subshells in the second shell. Insertion of diagonal lines in the manner shown gives the right order for filling the subshells.
Predict the electron configuration for each of the following atoms:
(a) \({}_{\text{15}}^{\text{31}}\text{P}\); (b) \({}_{\text{27}}^{\text{59}}\text{Co}\).
Solution
In each case we follow the rules just stated.
a) For \({}_{\text{15}}^{\text{31}}\text{P}\) there would be 15 protons and 16 neutrons in the nucleus and 15 extra nuclear electrons. Using Figure 1b to predict the order in which orbitals are filled, we have
1s2 2 electrons, leaving 15 – 2 = 13 more to add2s2 2 electrons, leaving 11 more to add
2p2x, 2p2y, 2p2z, (or 2p6) 6 electrons, leaving 5 more to add
3s2 2 electrons, leaving 3 more to add
3p1x, 3p1y, 3p1z 3 electrons
The electron configuration is thus \({}_{\text{15}}^{\text{31}}\text{P}\) 1s22s22p63s23p1x3p1y3p1z It could also be written [Ne]3s23p1x3p1y3p1z or [Ne]3s23p3 or where [Ne] represents the neon kernel 1s22s22p6. b) In the case of cobalt there is a total of 27 electrons to fill into the orbitals. There is no difficulty with the first 10 electrons. As in the previous example, they fill up the first and second shells: 1s22s22p6 17 more to add The third shell now begins to fill. First the 3s subshell then the 3p subshell are filled by 8 more electrons: 1s22s22p63s23p6 9 more to add Since this is also the structure of argon, we can use the shorthand form[Ar] 9 more to add
We now come to an energy overlap between the third and fourth shells. Because the 3d orbitals are so well shielded from the nucleus, they are higher in energy than the 4s orbitals. Accordingly the next orbitals to be filled are the 4s orbitals:
-
- [Ar]4s2 7 more to add
Once the 4s orbital is filled, the 3d orbitals are next in line to be filled. The 7 remaining electrons are insufficient to fill this subshell so that we have the final result
-
- [Ar]3d7 4s2
Electron configurations of the atoms may be determined experimentally. Table 1 in Electron Configurations and the Periodic Table lists the results that have been obtained. There are some exceptions to the four rules enunciated above, but they are usually relatively minor. An obvious example of such an exception is the structure of chromium. It is found to be [Ar]3d54s1, whereas our rules would have predicted [Ar]3d44s2. Chromium adopts this structure because it allows the electrons to avoid each other more effectively. A complete discussion of this and other exceptions is beyond the scope of an introductory text.


