5.8: Orbitals
- Page ID
- 49291
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A characteristic of the diagram Figure 1 in Electron Waves in the Hydrogen Atom is that it has been assigned an identifying label, namely, 1s. This enables us to distinguish it from other wave patterns the electron could possibly adopt if it moved about the nucleus with a higher energy. Each of these three-dimensional wave patterns is different in shape, size, or orientation from all the others and is called an orbital. The word orbital is used in order to make a distinction between these wave patterns and the circular or elliptical orbits of the Bohr picture shown in The Wave Nature of the Electron.
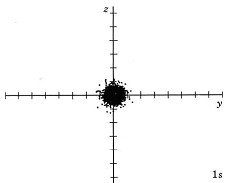
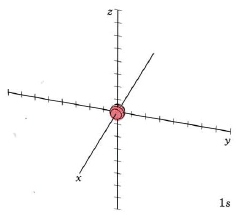
At ordinary temperatures, the electron in a hydrogen atom is almost invariably found to have the lowest energy available to it. That is, the electron occupies the 1s orbital. The electron cloud looks like the dot-density diagram shown in Figure 1 from Electron Waves in the Hydrogen Atom. This orbital is shown below as both a boundary surface diagram1 and a dot density diagram1
| Orbital | Dot Density Diagram(s) | Boundary Surface Diagram |
|---|---|---|
| 1s |
|
|
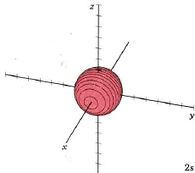
At a very high temperature, though, some collisions between the atoms are sufficiently hard to provide one of the electrons with enough energy so that it can occupy one of the other orbitals, say a 2s orbital, but this is unusual. Nevertheless, a knowledge of these higher energy orbitals is necessary since electron clouds having the same shapes as hydrogen are found to apply to all the other atoms in the periodic table as well. The 2s orbital is shown below, once again represented by a dot density diagram and a boundary surface diagram. Notice how the dot density diagram reveals a feature about the 2s orbital that boundary surface does not: A node divides the 2s orbital in two, a portion of the electron cloud is near the center, while another portion lies beyond the node (the circular region with no dots). At the node the wave has no amplitude, its square is also zero, and there is zero probability of finding the electron.
Table \(\PageIndex{2}\): 2s Orbital
| Orbital | Dot Density Diagram(s) | Boundary Surface Diagram |
|---|---|---|
| 2s |

|
|
In the case of a particle in a one-dimensional box, the energy was determined by a positive whole number n. Much the same situation prevails in the case of the hydrogen atom. An integer called the principal quantum number, also designated by the symbol n, is used to label each orbital. The larger the value of n, the greater the energy of the electron and the larger the average distance of the electron cloud from the nucleus. In the two orbitals already considered, n = 1 for the 1s orbital, n= 2 for the 2s orbital.
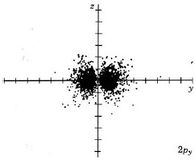
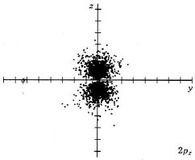
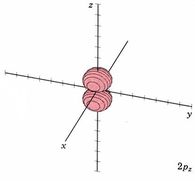
Because a greater number of different shapes is available in the case of three-dimensional, as opposed to one-dimensional, waves, two other labels are used in addition to n. The first consists of one of the lowercase letters s, p, d, or f. These tell us about the overall shapes of the orbitals.2 Thus all s orbitals such as the 1s, 2s are spherical. An important point is that only a limited number of orbital shapes is possible for each value of n. If n = 1, then only the spherical 1s orbital is possible. When n is increased to 2, though, two orbital types (2s and 2p) become possible. Thus along with the 2s orbital, 3 other orbitals exist when n=2; 2px, 2py, and 2pz. All p orbitals have a dumbbell shape. The third kind of label are subscripts which distinguish between orbitals which are basically the same shape but differ in their orientation in space. In the case of p orbitals there are always three orientations possible. A p orbital which extends along the x axis is labeled a px orbital. A p orbital along the y axis is labeled py and one along the z axis is a pz orbital. Below are dot density diagrams, boundary surface diagrams, and a rotating image. Using the moving images, it is easy to see that the only difference between the 2p orbitals is their orientation in xyz 3-coordinate space.
| Orbital | Dot Density Diagram(s) | Boundary Surface Diagram | Rotating Image |
|---|---|---|---|
| 2px |
|
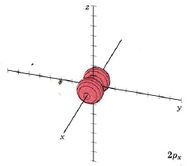
|
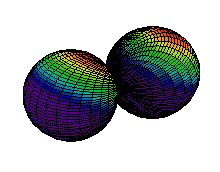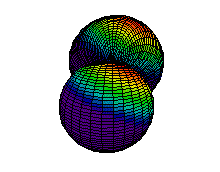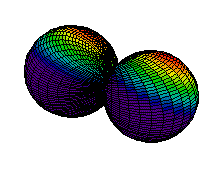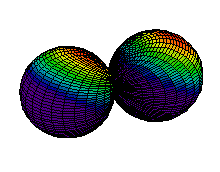
|
| 2py |

|
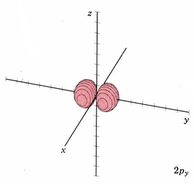
|
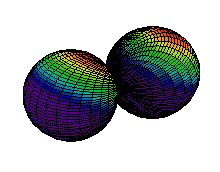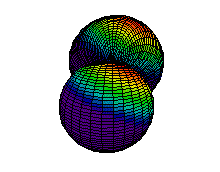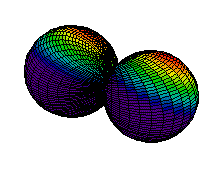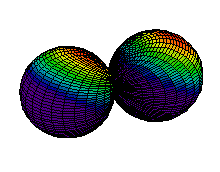
|
| 2pz |
|
|
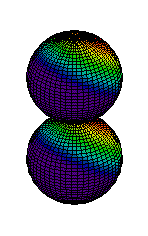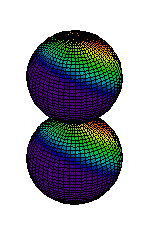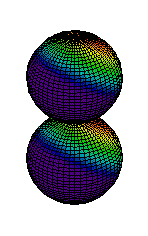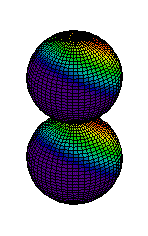
|
When n equals 3, three orbital types occur. The first two are familiar, the s orbital and p orbitals. The third, the d orbital, is discussed later. Below are representations of the 3s orbital, and the 3p orbitals. As the 2s orbital was slightly different in shape from the 1s orbital due to the introduction of a node, so the 3s and 3p orbitals differ slightly in shape from the 2s and 2p orbitals.
| Orbital | Dot Density Diagram(s) |
Boundary Surface Diagram |
|---|---|---|
| 3s |
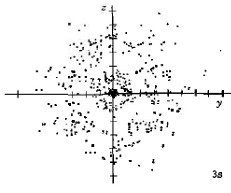
|
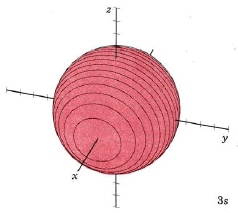
|
| 3px |
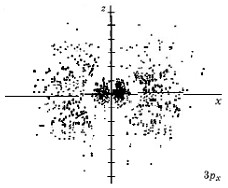
|

|
| 3py |
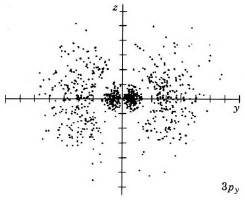
|
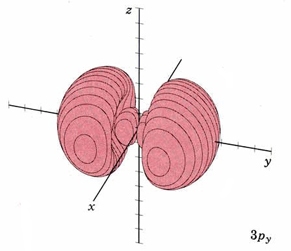
|
| 3pz |
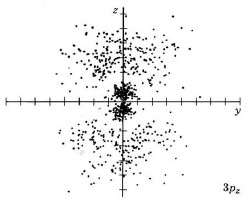
|
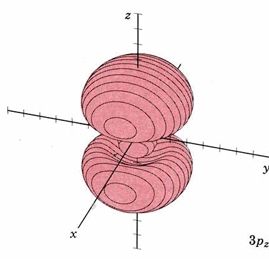
|
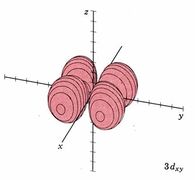
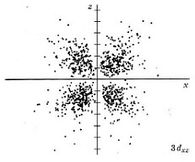
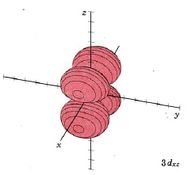
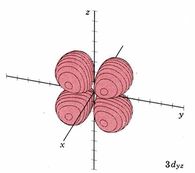
The d orbitals have more complex shapes than the p orbitals, In the case of the d orbitals the subscripts are more difficult to follow. You can puzzle them out from the rotating images, the dot density diagrams and the orbital surface diagrams if you like, but analysis of these orbitals is usually considered beyond the scope of general chemistry. You should, however, be aware that there are five possible orientations for d orbitals. Below are representations of the d orbitals.
| Orbital | Dot Density Diagram(s) | Boundary Surface Diagram | Rotating Image |
|---|---|---|---|
| 3dxy |
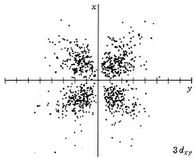
|
|
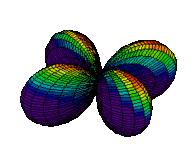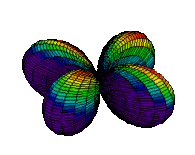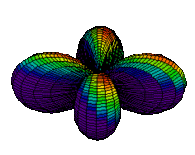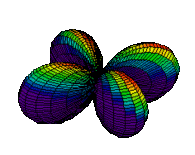
|
| 3dxz |
|
|
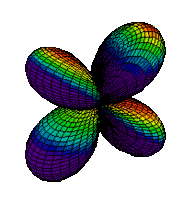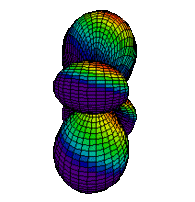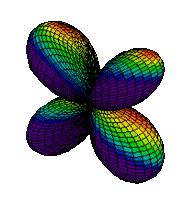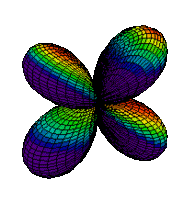
|
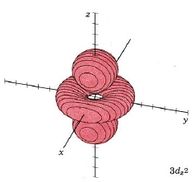
| 3dz2 |
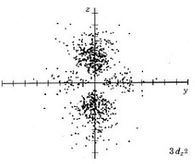
|
|
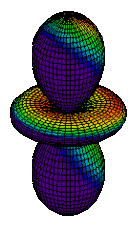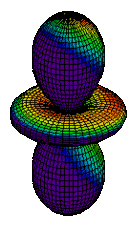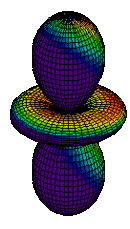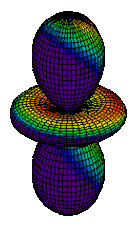
|
| 3dx2-y2 |
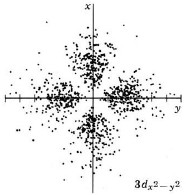
|
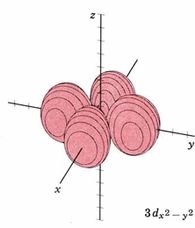
|
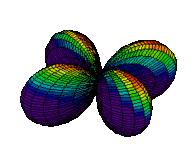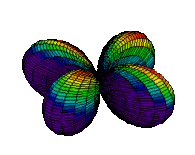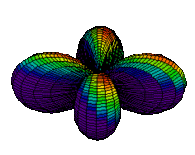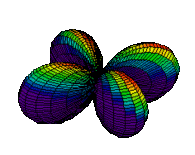
|
| 3dyz |

|
|
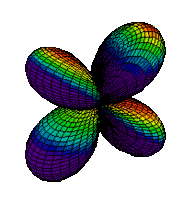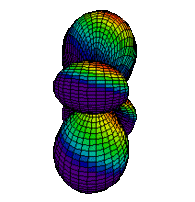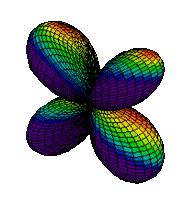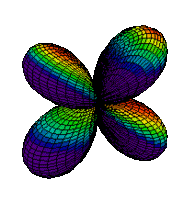
|
The same pattern extends to n = 4 where four orbital types, namely, 4s, 4p, 4d and 4f, are found. While none of these orbitals will be shown, the patterns seen in moving from 1s to 2s or from 2p to 3p continue with the s, p, and d orbitals. The new f orbitals are even more complicated than the d orbitals. For an understanding of general chemistry, it is important to know that there are seven different orientations for f orbitals, since the number of orbitals of each type (s, p, d, etc.) is important in determining the shell structure of the atom.
1 All dot density diagrams and boundary-surface diagrams are Copyright © 1975 by W. G. Davies and J. W. Moore.
2 The letters s, p, d and f originate from the words sharp, principal, diffuse and fundamental which were used to describe certain features of spectra before wave mechanics was developed. They later became identified with orbital shapes.


