5.8.1: Cultural Connections- Tones on a Drum and Orbital Wave Functions
- Page ID
- 50792
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A drummer can influence the pitch of a drum by touching its surface. A drum vibrates in a complicated way, but all the vibrations can be broken down into several "fundamental modes" of vibration (wavefunctions), like the ones we showed before and will further explain below.
Earlier we suggested that two Dimensional Standing Waves on a drum might help understand the wave patterns for electrons constrained to a nucleus. We'll now show how that works.
There are actual movies of the vibrations of a drum head on YouTube, but the cartoons below will make a number of modes easy to see.
We'll label the first set of modes m1,0, m2,0, and m3,0, or in general,mn,l. Later we'll see that the first number corresponds to the shell number, n, or "principal quantum number" of an atom, and the second to the "angular quantum number". In this first set, all the l ("el") values are 0.


mode m1,0


mode m2,0


mode m3,0
Note that all of these vibrate up and down in the middle, although the last two have circular nodes where they don't vibrate at all. For m2,0, if you start at "3:00--in the middle of the right side, and move the mouse pointer in about 7 graph markers from the right (about 1/3 to 1/2 of the way to the center), you'll find a node, where there is no vibration. If a drummer touched the drum here, it would not affect the second mode, but it would make the first and third modes impossible, because they don't have nodes here. The sound of the drum would change because two modes were eliminated. Note that the total number of nodes is n-1 (0 for m1,0, 1 for m2,0, and 2 for m3,0). In this case, all the nodes are circular nodes.


mode m2,1


mode m3,1


mode m4,1
Here's another set of vibrational modes, m2,1, m3,1, m4,1. Note that the second number, l "el", has changed from 0 to 1, and it tells us the number of linear nodes (planar nodes in 3D). We'll see later that l, corresponds to the angular quantum number for electrons. It may be difficult to see these node at first, but in mode m2,1 there is one linear node along a diagonal, so half the drum is displaced upwards, and half downwards. The other modes have one and two circular nodes, respectively, in addition to the diagonal linear node, because the total number of nodes must be n-1.
Finally, the set of modes below has l = 2, so that there are two planar nodes, which are two diagonals, perpendicular to each other. Thus mode m3,2 divides the drum into four quadrants, with alternate quadrants vibrating up and down, respectively. The other two modes have additional circular nodes.
|
 mode m3,2 |
 mode m4,2 |
 mode m5,2 |
Now let's look at 3 dimensional wavefunctions that might be used to describe the electron, compared to the 3 D drum vibrations. In three dimensions, the circular nodes will become spherical nodes, and the linear nodes will become planar nodes. We also use a shorthand designation for the shapes of wavefunctions, in which letters which are used to designate the values of l:
| l value | symbol | obsolete term / "mnemonic" |
| 0 | s | sharp / "spherical" |
| 1 | p | principal / "propeller" |
| 2 | d | diffuse / "daisy" (4 lobes) or "donut"(dz2) |
| 3 | f | fundamental / "flower" (8 lobes) |
| 4 | g... | and so on alphabetically |
So if n = 1 and l = 0, it's a "1s orbital"; if n = 3 and l = 2, it's a "3d orbital", and if n = 4 and l = 3, it's a "4f orbital", etc. We'll start with the lowest energy wavefunction, the one with the fewest nodes. It has n = 1, l = 0, so it's designated "1s". We'll show the 2D drum vibration, the 3D orbital as a rotatable Jmol model, and a "surface plot" where the surface is drawn so that the electron would be within it (typically) 95% of the time.
| Orbital designation | Drum Vibration | Rotating Orbital | Boundary Surface Diagram[1] |
| 1s |
 mode m1,0 |

|
We use the label "1s" to distinguish this pattern from other wave patterns the electron could possibly adopt if it moved about the nucleus with a higher energy. Each of these three-dimensional wave patterns is different in shape, size, or orientation from all the others and is called an orbital. The word orbital is used in order to make a distinction between these wave patterns and the circular or elliptical orbits of the Bohr picture shown in The Wave Nature of the Electron.
At ordinary temperatures, the electron in a hydrogen atom is almost invariably found to have the lowest energy available to it. That is, the electron occupies the 1s orbital. The electron cloud looks like the dot-density diagram shown in Figure 1 from Electron Waves in the Hydrogen Atom. This orbital is shown below as both a boundary surface diagram1, a dot density diagram1, and a rotatable Jmol.
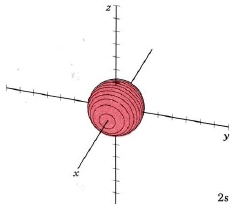
At a very high temperature, though, some collisions between the atoms are sufficiently hard to provide one of the electrons with enough energy so that it can occupy one of the other orbitals, say a 2s orbital, but this is unusual. Nevertheless a knowledge of these higher energy orbitals is necessary since electron clouds having the same shapes as for hydrogen are found to apply to all the other atoms in the periodic table as well. The 2s orbital is shown below, once again represented by a dot density diagram, a boundary surface diagram, and a rotatable Jmol. Notice how the dot density diagram reveals a feature about the 2s orbital that boundary surface does not: Since n = 2 and l = 0, there must one "spherical" node. A node divides the 2s orbital in two, a portion of the electron cloud is near the center, while another portion lies beyond the node (the circular region with no dots). At the node the wave has no amplitude, its square is also zero, and there is zero probability of finding the electron. This additional node accounts, in part, for the higher energy of the 2s orbital.
| Orbital designation | Drum Vibration | Rotating Orbital | Boundary Surface Diagram |
| 2s |
 mode m2,0 |
|
In the case of a particle in a one-dimensional box or drum vibrations, the energy was determined by a positive whole number n. The same situation prevails in the case of the hydrogen atom. An integer called the principal quantum number, also designated by the symbol n, is used to label each orbital. The larger the value of n, the greater the energy of the electron and the larger the average distance of the electron cloud from the nucleus. In the two orbitals already considered, n = 1 for the 1s orbital, n= 2 for the 2s orbital.
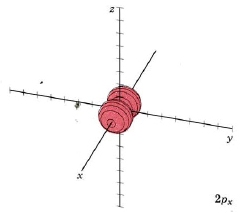
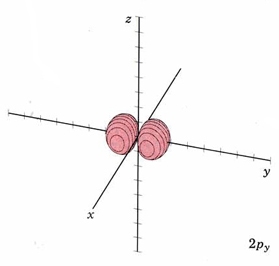
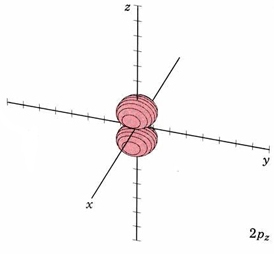
For the second shell, n=2, the total number of nodes is 1, so l may have values of 0 or 1 (since there may be 0 or 1 planar node). If l = 1 we get a new set of orbitals, designate 2p with one planar node. In the H atom, these orbitals have the same energy as the 2s orbitals because they have the same number of nodes, but when more electrons are added, they have different energies. Since there are three independent planes defined by 3D geometry (each slicing through the x, y or z axis), there must be three orbitals with 1 planar node. They are designated 2px, 2py, and 2pz. This is analogous to the 2D drum vibrations, where there are 2 perpendicular lines defining the nodes. The boundary diagrams show why the mnemonic "propeller" might be appropriate.
| Orbital designation | Drum Vibration | Rotating Orbital | Boundary Surface Diagram | |
| 2px |
 mode m2,1 nodal plane yz |
|
||
| 2py |
 mode m2,1 nodal plane xz |
|
||
| 2pz |
 mode m2,1 nodal plane xy |
|
|
When n equals 3, there are 2 nodes, and l may have values of 0, 1, or 2 (since there may be 0, 1, or 2 planar nodes). The first two are familiar, the s orbital and p orbitals. Below are representations of the 3s orbital, and the 3p orbitals. As the 2s orbital was slightly different in shape from the 1s orbital due to the introduction of a node, so the 3s and 3p orbitals differ slightly in shape from the 2s and 2p orbitals.
| Orbital designation | Drum Vibration | Boundary Surface Diagram |
| 3s |
 mode m3,0 |

|
| 3px |
 mode m3,1 nodal plane yz |
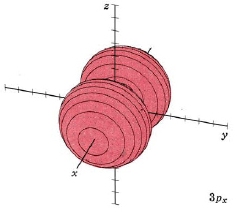
|
| 3py | as above, nodal plane xz |
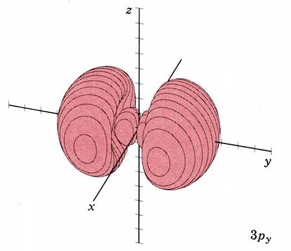
|
| 3pz | as above, nodal plane xy |
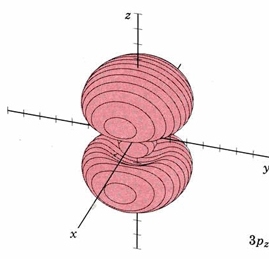
|
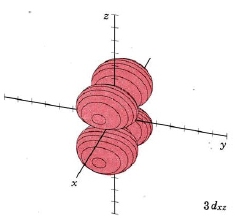
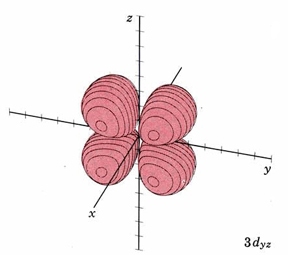
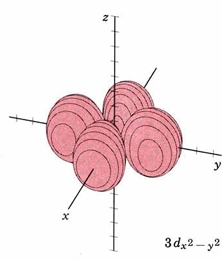
In the third shell there are 2 nodes, and for the drum, they may both be linear, when l = 2. In 3D, this gives rise to the "d orbitals", with 4-lobed "daisy" wavefunctions, each having 2 perpendicular planar nodes. In the case of the d orbitals the subscripts are more difficult to follow. You can puzzle them out from the Jmols, the dot density diagrams and the orbital surface diagrams if you like, but analysis of these orbitals is usually considered beyond the scope of general chemistry. You should, however, be aware that there are five possible orientations for d orbitals. Below are representations of the d orbitals. Since all have 2 nodes, they all have the same energy in the hydrogen atom, but different energies when more electrons are added.
| Orbital designation | Drum Vibration | Rotating Orbital | Boundary Surface Diagram |
| 3dxy |
 mode m3,2 nodal planes xz and yz |
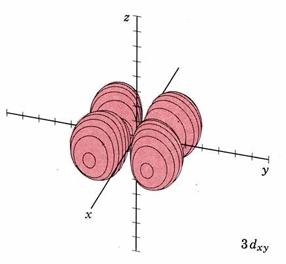
|
|
| 3dxz | same as above, nodal planes xy and zy |
|
|
| 3dyz | same as above, nodal planes xy and xz |
|
|
| 3dx2-y2 | same as above, nodal planes thru z bisecting x,y |
|
|
| 3dz2 | no corresponding mode; funnel shaped nodal planes |
|

|
The same pattern extends to n = 4 where four orbital types, namely, 4s, 4p, 4dand 4f, are found. While none of these orbitals will be shown, the patterns seen in moving from 1s to 2s or from 2p to 3p continue with the s, p, and d orbitals. The new f orbitals are even more complicated than the d orbitals. For an understanding of general chemistry, it is important to know that there are seven different orientations for f orbitals, since the number of orbitals of each type (s, p, d, etc.) is important in determining the shell structure of the atom.
Orbitals on the Web
Orbitron: [1] D. Manthey's Orbital Viewer: [2] Falstad.com: [3] JCE: [4] Darmstadt: [5] [6]
References
- ↑ 1 All dot density diagrams and boundary-surface diagrams are Copyright © 1975 by W. G. Davis and J. W. Moore.










