5.15: Beryllium, Boron, Carbon
- Page ID
- 49335
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Beryllium
As shown below, there are two 1s electrons and two 2s electrons in the Be atom. Its electron configuration is thus
\[1s^{2}2s^{2} \ce{or [He]}2s^{2} \nonumber \]
The symbol [He] denotes the inner shell of two 1s electrons which have the same configuration as the noble gas He.
The beryllium atom is noticeably smaller than the lithium atom. This is because of the increase in nuclear charge from +3 to +4. Since the two outer 2s electrons (red and orange) do not often come between each other and the nucleus, they do not screen each other from the nucleus very well. Only the two inner electrons are effective in this respect. The effective nuclear charge holding a 2s electron to the nucleus is thus nearly +2, about twice the value for lithium, and the 2s electron clouds are drawn closer to the center of the atom.
Boron
The next element after beryllium is boron. Since the 2s orbital is completely filled, a new type of orbital must be used for the fifth electron. There are three 2p orbitals available, and any of them might be used. Plate 5 shows the fifth electron (color-coded purple) occupying the 2px orbital. Note carefully the differences between the 2px and 2s electron density distributions in the boron atom. Although on the average both electron clouds extend about the same distance from the nucleus, the 2px electron wave has a node passing through the center of the atom. Thus the 2px electron cloud has a much smaller probability density very close to the nucleus than does a 2s cloud. This means that the 2px electron cloud is more effectively screened by the 1s electrons from the nuclear charge. The atom exerts a slightly smaller overall pull on the 2p electron than it does on the 2s electron. The presence of the inner electrons thus has the effect of making the 2p orbital somewhat higher in energy than the 2s orbital.
This difference in energy between 2s and 2p electrons in the boron atom is an example of a more general behavior. In any atom with sufficient electrons we always find that a p orbital is somewhat higher in energy than an s orbital with the same value of n. In the lithium atom, for example, the third electron occupies a 2s rather than a 2p orbital because this gives it a somewhat lower energy. Further on in the periodic table we will find a similar difference between 3s and 3p orbitals and between 4s and 4p orbitals.
Carbon
We shall examine the electron configuration of one more atom, carbon, with the aid of the color-coded diagrams. In this case six electrons must be distributed among the orbitals—four will be paired in the 1s and 2s orbitals, leaving two p-type electron clouds. These are shown color-coded purple and cyan in Plate 5 as 2px and 2py, although the choice of x, y, or z directions is arbitrary. The choice of two different p orbitals is not arbitrary, however. It can be shown experimentally that both p electrons in the carbon atom have the same spin. Hence they cannot occupy the same orbital.
This illustrates another general rule regarding electron configurations. When several orbitals of the came type but different orientation are available, electrons occupy them one at a time, keeping spins parallel, until forced to pair by lack of additional empty orbitals. This is known as Hund's rule. Thus the electron configuration of carbon is
\[\ce{[He]}2s^{2} 2p_{x}^{1} 2p_{y}^{1} \nonumber \]
This might also be written (using arrows to indicate the orientations of electron spins):
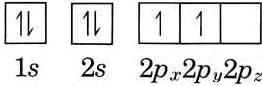
The notation \(\ce{[He]}2s^{2}2p^{2}\) may also be found. In such a case it is assumed that the reader knows that the two 2p electrons are not spin paired.
It is worth noting that the arrangement of electrons in different 2p orbitals, necessitated by Hund’s rule, produces a configuration of lower energy. If both 2p electrons could occupy the same orbital, say the 2px orbital, they would often be close to each other, and their mutual repulsion would correspond to a higher potential energy. If each is forced to occupy an orbital of different orientation, though, the electrons keep out of each other’s way much more effectively. Their mutual repulsion and hence their potential energy is less.
In talking about polyelectronic atoms, the terms shell and subshell are often used. When the two electrons have the same principal quantum number, they are said to belong to the same shell. In the carbon atom, for example, the two 2s electrons and the 2px and the 2py electrons all belong to the second shell, while the two 1s electrons belong to the first shell. Shells defined in this manner can be further divided into subshells according to whether the electrons being discussed occupy s, p, d, or f orbitals. We can thus divide the second shell into 2s and 2p subshells. The third shell can similarly be divided into 3s, 3p, and 3d subshells, and so on.


