5.14: Hydrogen, Helium, Lithium
- Page ID
- 49333
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)With some familiarity with the properties of single electrons, such as the single electron around the hydrogen nucleus above, we can discuss atoms containing more than one electron. The images found here depict electron wave density by number of dots. Thus, more dots indicates more electron density 'cloud' in that region. In these diagrams, each electron wave is displayed with a different color and you can toggle the view of each electron wave on and off using the buttons below the dot density diagrams.
Helium
The first element in the periodic table with more than one electron is helium, which has two electrons. Dot-density diagrams for both these electrons are shown below. One electron is color coded in blue, and the other in green. Note that both electrons occupy the same orbital, namely, a 1s orbital. It turns out that 2 is the maximum number of electrons any orbital can hold. This restriction is connected with a property of the electrons not yet discussed, namely, their spin. Electrons can not only move about from place to place, but they can also rotate or spin about themselves. Two orientations (clockwise and counterclockwise, referred to as spin up or spin down) are possible for this spin. According to the Pauli exclusion principle, if two electrons occupy the same orbital, they must have opposite spins. Two such electrons are said to be spin paired and are often represented by arrows pointing in different directions, i.e., by the symbol 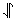 . Two electrons spinning in the same direction are said to have their spins parallel and are indicated by
. Two electrons spinning in the same direction are said to have their spins parallel and are indicated by 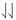 . The Pauli principle implies that if two electrons have parallel spins, they must occupy different orbitals.
. The Pauli principle implies that if two electrons have parallel spins, they must occupy different orbitals.
An obvious feature of the helium atom shown below is that it is somewhat smaller than the hydrogen atom drawn to the same scale above. This contraction is caused by the increase in the charge on the nucleus from +1 in the hydrogen atom to +2 in the helium atom. This pulls both the green and the blue electron clouds in more tightly. This effect is offset, but to a lesser extent, by the mutual repulsion of the two electron clouds.
Lithium
In the dot density image below, the three electrons of the lithium atom are color-coded blue, green, and red. As in the previous atom, two electrons (blue and green) occupy the 1s orbital. The Pauli principle prevents more than two electrons from occupying this orbital, and so the third (red) electron must occupy the next higher orbital in energy, namely, the 2s orbital. A convenient shorthand form for indicating this electron configuration is
1s22s1
The superscripts 2 and 1 indicate that there are two electrons in the 1s orbital and one electron in the 2s orbital, respectively.
As in the case of helium, the increase in nuclear charge to +3 produces a corresponding reduction in the size of the lithium 1s orbital. In sharp contrast to this compact inner orbital is the very large and very diffuse cloud of the outer 2s electron. There are two reasons why this 2s cloud is so large. The first reason is that the principal quantum number n has increased from 1 to 2. As shown in Figure 1 of the Orbitals page, the 2s electron cloud is bigger than 1s even in the hydrogen atom with a nuclear charge of only +1. A second reason is that the two 1s electrons are usually closer to the nucleus than the 2s electron. These two 1s electrons have the effect of screening or shielding the outer electron from the full attractive force of the +3 charge on the nucleus. When the 2s electron is some distance from the nucleus, it “sees” not only the +3 charge on the nucleus but also the two negative charges close by. The overall effect is almost as though two of the three positive charges on the nucleus are canceled, leaving a net charge of + 1 to hold the outer electron to the atom. This situation can also be described by saying that the effective nuclear charge is close to +1.
It should be clear from Plate 4 that when a lithium atom interacts with another atom, the 2s electron is far more likely to be involved than either of the two 1s electrons. In Lewis’ terminology, it is a valence electron and occupies a valence shell. The pair of 1s electrons are a complete shell and form the kernel of the lithium atom. There is thus a close correspondence between the wave-mechanical picture and Lewis’ earlier, less mathematical ideas. It is also worth noting that the wave model of lithium gives a spherical atom―a great advance over the elongated orbits which were needed to describe the alkali-metal atoms in the Bohr theory (see image of the Bohr atom).


