17.4: Reaction Mechanisms

Learning Objectives

Make sure you thoroughly understand the following essential ideas which have been presented above. It is especially important that you know the precise meanings of all the green-highlighted terms in the context of this topic.

• Explain what is meant by the mechanism of a reaction.
• Define an elementary reaction, and state how it differs from an ordinary net chemical reaction.
• Sketch out an activation energy diagram for a multistep mechanism involving a rate-determining step, and relate this to the activation energy of the overall reaction.
• Write the rate law expression for a two-step mechanism in which the rate constants have significantly different magnitudes.
• Write the rate law expression for a three-step reaction in which one step is a rapid equilibrium, and the other two steps have significantly different magnitudes.
• Define a chain reaction, and list some of the different kinds of steps such a reaction will involve.
• Define a branching chain reaction, and explain how such reactions can lead to explosions.

We are now ready to open up the "black box" that lies between the reactants and products of a net chemical reaction. What we find inside may not be very pretty, but it is always interesting because it provides us with a blow-by-blow description of how chemical reactions take place.

The mechanism of a chemical reaction is the sequence of actual events that take place as reactant molecules are converted into products. Each of these events constitutes an elementary step that can be represented as a coming-together of discrete particles ("collision") or as the breaking-up of a molecule ("dissociation") into simpler units. The molecular entity that emerges from each step may be a final product of the reaction, or it might be an intermediate — a species that is created in one elementary step and destroyed in a subsequent step, and therefore does not appear in the net reaction equation.

For an example of a mechanism, consider the decomposition of nitrogen dioxide into nitric oxide and oxygen. The net balanced equation is

\[\ce{2 NO2(g) → 2 NO(g) + O2(g)} \nonumber\]

The mechanism of this reaction is believed to involve the following two elementary steps:

\[ \begin{align*} \ce{2 NO2} &→ \ce{NO3 + NO} \label{step 1} \\[4pt] \ce{NO3} &→ \ce{NO + O2} \label{step 2} \end{align*}\]

Note that the intermediate species \(\ce{NO3}\) has only a transient existence and does not appear in the net equation.

Properties of a Mechanism

A useful reaction mechanism

• consists of a series of elementary steps (defined below) that can be written as chemical equations, and whose sum gives the net balanced reaction equation;
• must agree with the experimental rate law;
• can rarely if ever be proved absolutely.

It is important to understand that the mechanism of a given net reaction may be different under different conditions. For example, the dissociation of hydrogen bromide

\[\ce{2 HBr(g) → H2(g) + Br2(g)} \nonumber\]

proceeds by different mechanisms (and follows different rate laws) when carried out in the dark (thermal decomposition) and in the light (photochemical decomposition). Similarly, the presence of a catalyst can enable an alternative mechanism that greatly speeds up the rate of a reaction.

Elementary Steps

A reaction mechanism must ultimately be understood as a "blow-by-blow" description of the molecular-level events whose sequence leads from reactants to products. These elementary steps (also called elementary reactions) are almost always very simple ones involving one, two, or [rarely] three chemical species which are classified, respectively, as

unimolecular	\(A →\)	by far the most common
bimolecular	\(A + B →\)	common
termolecular	\(A + B + C →\)	very rare

Elementary reactions differ from ordinary net chemical reactions in two important ways:

• The rate law of an elementary reaction can be written by inspection. For example, a bimolecular process always follows the second-order rate law \(rate=k[A][B]\).
• Elementary steps often involve unstable or reactive species that do not appear in the net reaction equation.

Some net reactions do proceed in a single elementary step, at least under certain conditions. However, without careful experimentation, one can never be sure. The gas-phase formation of \(\ce{HI}\) from its elements was long thought to be a simple bimolecular combination of \(\ce{H2}\) and \(\ce{I2}\), but it was later found that under certain conditions, it follows a more complicated rate law.

Multi-step (Consecutive) Reactions

Mechanisms in which one elementary step is followed by another are very common.

\[\ce{ A + B → \cancel{Q} } \tag{step 1}\]

\[\ce{B + \cancel{Q} → C} \tag{step 2}\]

\[\ce{A + 2B → C} \tag{net reaction}\]

(As must always be the case, the net reaction is just the sum of its elementary steps.)

In this example, the species \(Q\) is an intermediate, usually an unstable or highly reactive species. If both steps proceed at similar rates, rate law experiments on the net reaction would not reveal that two separate steps are involved here. The rate law for the reaction would be

\[rate = k[A][B]^2 \nonumber\]

(Bear in mind that intermediates such as \(Q\) cannot appear in the rate law of a net reaction.)

When the rates are quite different, things can get interesting and lead to quite varied kinetics as well as some simplifying approximations. When the rate constants of a series of consecutive reactions are quite different, a number of relationships can come into play that greatly simplify our understanding of the observed reaction kinetics.

Approximation 1: The Rate-Determining Step Approximation

The rate-determining step is also known as the rate-limiting step. We can generally expect that one of the elementary reactions in a sequence of consecutive steps will have a rate constant that is smaller than the others. The effect is to slow the rates of all the reactions — very much in the way that a line of cars creeps slowly up a hill behind a slow truck.

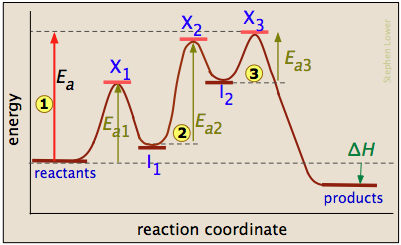
The three-step reaction depicted here involves two intermediate species I₁ and I₂, and three activated complexes numbered X_1-3. Although the step I ₂ → products has the smallest individual activation energy E_a3, the energy of X₃ with respect to the reactants determines the activation energy of the overall reaction, denoted by the leftmost vertical arrow . Thus the rate-determining step is

\[X_1 → X_2. \nonumber\]

Chemists often refer to elementary reactions whose forward rate constants have large magnitudes as "fast", and those with forward small rate constants as "slow". Always bear in mind, however, that as long as the steps proceed in single file (no short-cuts!), all of them will proceed at the same rate. So even the "fastest" members of a consecutive series of reactions will proceed as slowly as the "slowest" one.

Approximation 2: The Rapid Equilibrium Approximation

In many multi-step processes, the forward and reverse rate constants for the formation of an intermediate \(Q\) are of similar magnitudes and sufficiently large to make the reaction in each direction quite rapid. Decomposition of the intermediate to product is a slower process:

\[\ce{A <=>[k_1][k_{-1}] Q ->[k_2] B} \nonumber\]

This is often described as a rapid equilibrium in which the concentration of \(Q\) can be related to the equilibrium constant

\[K = \dfrac{k_1}{k_{–1}} \nonumber\]

This is just the Law of Mass Action. It should be understood, however, that true equilibrium is never achieved because \(Q\) is continually being consumed; that is, the rate of formation of \(Q\) always exceeds its rate of decomposition. For this reason, the steady-state approximation described below is generally preferred to treat processes of this kind.

Approximation 3: The Steady-State Approximation

Consider a mechanism consisting of two sequential reactions

\[\ce{A ->[k_1] Q ->[k_2] B} \nonumber\]

in which \(Q\) is an intermediate. The time-vs-concentration profiles of these three substances will depend on the relative magnitudes of \(k_1\) and \(k_2\), as shown in the following diagrams. Construction of these diagrams requires the solution of sets of simultaneous differential equations, which is [fortunately!] beyond the scope of this course.

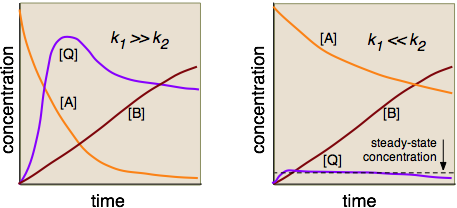
The steady-state approximation is usually not covered in introductory courses, although it is not particularly complicated mathematically.

In the left-hand diagram, the rate-determining step is clearly the conversion of the rapidly-formed intermediate into the product, so there is no need to formulate a rate law that involves \(Q\). But on the right side, the formation of \(Q\) is rate-determining, but its conversion into \(B\) is so rapid that \([Q]\) never builds up to a substantial value. (Notice how the plots for \([A]\) and \([B]\) are almost mutually inverse.) The effect is to maintain the concentration of \(Q\) at an approximately constant value. This steady-state approximation can greatly simplify the analysis of many reaction mechanisms, especially those that are mediated by enzymes in organisms.

Converting Mechanisms into Rate Laws

We are unable to look directly at the elementary steps hidden within the "black box" of the reaction mechanism, we are limited to proposing a sequence that would be consistent with the reaction order which we can observe. Chemical intuition can guide us in this, for example by guessing the magnitudes of some of the activation energies. In the end, however, the best we can do is to work out a mechanism that is plausible; we can never "prove" that what we come up with is the actual mechanism.

Example \(\PageIndex{1A}\): A + B → C

Consider the following reaction:

\[A + B → C\nonumber\]

One possible mechanism might involve two intermediates \(Q\) and \(R\):

Step 1	\(\ce{A + B ->[k_1] Q}\)	(slow, rate-determining)
Step 2	\(\ce{Q + A ->[k_2] R }\)	(fast)
Step 3	\(\ce{ R + B ->[k_3] C }\)	(fast)

The rate law corresponding to this mechanism would be that of the rate-determining step:

\[\text{rate} = k_1[A][B]. \nonumber\]

If the first step in a mechanism is rate-determining, it is easy to find the rate law for the overall expression from the mechanism. If the second or a later step is rate-determining, determining the rate law is slightly more complicated and often requires either of the two approximation above to identify.

Example \(\PageIndex{1B}\): A + B → C

An alternative mechanism for the following reaction:

\[A + B → C \nonumber\]

in which the rate-determining step involves one of the intermediates would display third-order kinetics:

Step 1	\(\ce{A + B <=>[k_1][k_{-1}] Q}\)	(rapid equilibrium)
Step 2	\(\ce{Q + A ->[k_2] R }\)	(slow, rate-determining)
Step 3	\(\ce{ R + B ->[k_3] C }\)	(fast)

Since intermediates cannot appear in rate law expressions, we must express \([Q]\) in the rate-determining step in terms of the other reactants. To do this, we make use of the fact that Step 1 involves an equilibrium constant \(K_1\):

\[K_1 = \dfrac{k_1}{k_{-1}} = \dfrac{[Q]}{[A][B]} \nonumber\]

Solving this for \([Q]\), we obtain

\[[Q] = K_1[A][B]. \nonumber \]

We can now express the rate law for 2 as

\[\begin{align*} \text{rate} &= k_2 K_1[A][B][A] \\[4pt] &= k[A]^2[B] \end{align*}\]

in which the constants \(k_2\) and \(K_1\) have been combined into a single constant \(k\).

Example \(\PageIndex{2}\): F₂ + 2 NO₂ → 2 NO₂F

Consider the following reaction:

\[\ce{ F2 + 2 NO2 → 2 NO2F }\nonumber\]

Application of the "chemical intuition" mentioned in the above box would lead us to suspect that any process that involves breaking of the strong F–F bond would likely be slow enough to be rate limiting, and that the resulting atomic fluorines would be very fast to react with another odd-electron species:

Step 1	\(\ce{F2 + 2 NO2 ->[k_1] NO2F + F + NO2}\)	(slow, rate-determining)
Step 2	\(\ce{F + NO2 ->[k_2] NO2F}\)	(very fast)

If this mechanism is correct, then the rate law of the net reaction would be that of the rate-determining step:

\[\text{rate} = k_1[F_2][NO_2] \nonumber\]

Example \(\PageIndex{3}\): Decomposition of ozone

Ozone is an unstable allotrope of oxygen that decomposes back into ordinary dioxygen according to the net reaction

\[\ce{2 O3 → 3 O2} \nonumber\]

A possible mechanism would be the simple one-step bimolecular collision suggested by the reaction equation, but this would lead to a second-order rate law which is not observed. Instead, experiment reveals a more complicated rate law:

\[\text{rate} = [O_3]^2[O_2]^{–1} \nonumber\]

What's this? It looks as if O₂ actually inhibits the reaction in some way. The generally-accepted mechanism for this reaction is:

Step 1	\(\ce{O3 <=>[k_1][k_{-1}] O2+ O}\)	(rapid equilibrium)
Step 2	\(\ce{O + O3 ->[k_2] 2 O2}\)	(rate-determining)

Does this seem reasonable? Note that

• The equilibrium in Step 1 should be quite rapid because ozone's instability predicts a low activation energy for the forward process. The same can be said for the reverse process which involves the highly reactive oxygen atom which we would expect to rapidly gobble up one of the nonbonding electron pairs on the O₂ molecule.
• The inhibitory effect of O₂ can be explained by the Le Chatelier effect — being a product of the equilbrium in 1, buildup of oxygen forces it back to the left.
• In Step 2, one might expect the O atom to react with ozone as rapidly as it does with O₂ in the reverse of Step 1, but other studies show that this is not the case. The rate constant k₂ is probably fairly large. Given the strong covalent bond in O₂, we not expect any significant reverse reaction.

To translate this mechanism into a rate law, we first write the equilibrium constant for Step 1 and solve it for the concentration of the intermediate:

\[ K =\dfrac{[O_2][O]}{[O_3]} \nonumber\]

\[[O] = \dfrac{k_1[O_3]}{k_{-1}[O_2]} \nonumber\]

We substitute this value of \(\ce{[O]}\) into the rate expression \(\ce{[O][O3]}\) for Step 2, which yields the experimentally-obtained rate law

\[ rate = k_1K \dfrac{[O_3]^2}{[O_2]} \nonumber\]

Example \(\PageIndex{4}\): A reaction having an apparently Negative E_a

Consider the gas-phase oxidation of nitric oxide:

\[\ce{2 NO + O_2 → 2 NO_2} \nonumber\]

This reaction, like most third-order reactions, is not termolecular but rather a combination of an equilibrium followed by a subsequent bimolecular step:

Step 1	\(\ce{ NO + NO <=>[k_1][k_{-1}] N2O2}\)	(equilibrium, eq. const. K)
Step 2	\(\ce{ N2O2 + O2 ->[k_2] 2 NO2}\)	(rate-limiting)

Since the intermediate \(\ce{N2O2}\) may not appear in the rate equation, we need to express its concentration in terms of the reactant \(NO\). As in the previous example, we do this through the equilibrium constant of Step 1:

\[K = \dfrac{[N_2O_2]}{[NO]^2} \nonumber\]

\[[N_2O_2] = K [NO]^2 \nonumber\]

\[ \begin{align*} \text{rate} &= k_2 [N_2O_2 ][O_2] \\[4pt] &= k_2 K [NO]^2 [O_2] \end{align*} \]

The unusual feature of this net reaction is that its rate diminishes as the temperature increases, suggesting that the activation energy is negative. Reaction 1 involves bond formation and is exothermic, so as the temperature rises, \(K\) decreases (Le Chatelier effect). At the same time, k₂ increases, but not sufficiently to overcome the decrease in \(K\). So the apparently negative activation energy of the overall process is simply an artifact of the magnitudes of the opposing temperature coefficients of k₂ and \(K\).

Chain Reactions (Positive Feedback Mechanisms)

Many important reaction mechanisms, particularly in the gas phase, involve intermediates having unpaired electrons, commonly known as free radicals. Free radicals are often fairly stable thermodynamically and may be quite long-lived by themselves, but they are highly reactive, and hence kinetically labile. The dot ·, representing the unpaired electron, is not really a part of the formula, and is usually shown only when we want to emphasize the radical character of a species. The "atomic" forms of many elements that normally form diatomic molecules are free radicals; H·, O·, and Br· are common examples. The simplest and most stable (ΔG = +87 kJ/mol) molecular free radical or "odd-electron molecule" is nitric oxide, NO·.

The most important chemical property of a free radical is its ability to pass the odd electron along to another species with which it reacts. This chain-propagation process creates a new radical which becomes capable of initiating another reaction. Radicals can, of course, also react with each other, destroying both ("chain termination") while creating a new covalent-bonded species.

Max Bodenstein

Much of the pioneering work in this field, of which the \(\ce{HBr}\) synthesis is a classic example, was done by the German chemist Max Bodenstein (1871-1942)

The synthesis of hydrogen bromide from its elements illustrates the major features of a chain reaction. The figures in the right-hand column are the activation energies per mole.

Step 1	Br2 + M → 2 Br·	chain initiation (ΔH° = +188 kJ)
Step 2	Br· + H2 → H· + HBr	chain propagaton (+75 kJ)
Step 3	H· + Br2 → HBr + Br·	chain propagation (–176 kJ)
Step 4	H· + HBr → H2 + Br·	chain inhibition (–75 kJ)
Step 5	2 Br· + M → M* + Br2	chain termination (–188 kJ)

Note the following points:

• To start the reaction, a free radical must be formed (1). If the temperature of the gas is fairly high, then Br· can be formed from the more energetic collisions of Br₂ molecules with some other molecule M (most likely a second Br₂). This is known as thermal activation; Another way of creating free radicals is photochemical activation.
• Reactions 2 and 3 consume a free radical but form another, thus "propagating" the chain.
• In reaction 4, a molecule of the product is destroyed, thus partially un-doing the net process.
• If the only the first four reactions were active, then the cycle would continue indefinitely. But reaction 5 consumes the Br· chain carrier without producing new radicals, thus terminating the chain. The function of the molecule M is to absorb some of the kinetic energy of the collision so that the two bromine atoms do not simply bounce apart. The product M* represents a thermally-excited M which quickly dissipates its energy to other molecules.
• Other reactions, such as the recombination of hydrogen atoms, also take place, but their contribution to the overall kinetics is usually very small.

The rate laws for chain reactions tend to be very complex, and often have non-integral orders.

Branching Chain Reactions: Explosions

The gas-phase oxidation of hydrogen has been extensively studied over a wide range of temperatures and pressures.

\[\ce{H2(g) + 1/2 O2(g) → H2O(g)}\quad ΔH^o = –242\, kJ/mol \nonumber\]

This reaction does not take place at all when the two gases are simply mixed at room temperature. At temperatures around 500-600°C it proceeds quite smoothly, but when heated above 700° or ignited with a spark, the mixture explodes. As with all combustion reactions, the mechanism of this reaction is extremely complex (you do not want to see the rate law!) and varies somewhat with the conditions. Some of the major radical formation steps are

Step 1	H2 + O2 → HO2· + H·	chain initiation
Step 2	H2 + HO2· → HO· + H2O	chain propagaton
Step 3	H· + O2 → HO· + O·	chain propagaton + branching
Step 4	O· + H2 → HO· + H·	chain propagation + branching
Step 5	HO· + H2 → H2O + H·	chain propagation
The species HO2· is known as perhydroxyl; HO· is hydroxyl (not to be confused with the hydroxyl ion HO:^–)

Reactions 3 and 4 give birth to more radicals than they consume, so when these are active, each one effectively initiates a new chain process causing the rate overall rate to increase exponentially, producing an explosion.

Explosion Limits

An explosive reaction is a highly exothermic process that once initiated, goes to completion very rapidly and cannot be stopped. The destructive force of an explosion arises from the rapid expansion of the gaseous products as they absorb the heat of the reaction. There are two basic kinds of chemical explosions:

• Thermal explosions occur when heat is released by a reaction more rapidly than it can escape from the reaction space. This causes the reaction to proceed more rapidly, releasing even more heat, resulting in an ever-accelerating runaway rate.
• Chain-branching explosions occur when the number of chain carriers increases exponentially, effectively seeding new reaction centers in the mixture. The process then transforms into a thermal explosion.

Whether or not a reaction proceeds explosively depends on the balance between formation and destruction of the chain-carrying species. This balance depends on the temperature and pressure, as illustrated here for the hydrogen-oxygen reaction.

• Direct recombination of chain carriers generally requires a three-body collision with another molecule to absorb some of the kinetic energy; such ternary processes are unlikely at very low pressures. Thus below the lower explosion limit , the radicals (including those produced by a spark) are usually able to reach the walls of the container and combine there — or in the case of an open-air explosion, simply combine with other molecules as they exit the active volume of the reaction.
• Within the explosion zone between and (which, for most gases, are known as the lower- and upper explosion limits), the propagation and branching processes operate efficiently and explosively, even when the mixture is heated homogeneously.
• Above , the concentration of gas molecules is sufficient to enable ternary collisions which allow chain-termination processes to operate efficiently, thus suppressing branching. Above this upper limit, reactions involving most gases proceed smoothly.
• Hydrogen is unusual in that it exhibits a third explosion limit . The cause of this was something of a mystery for some time, but it is now believed that explosions in this region do not involve branching, but are thermally induced by the reaction
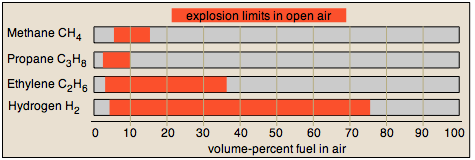
  HO₂· + H₂ → H₂O₂ + H· .

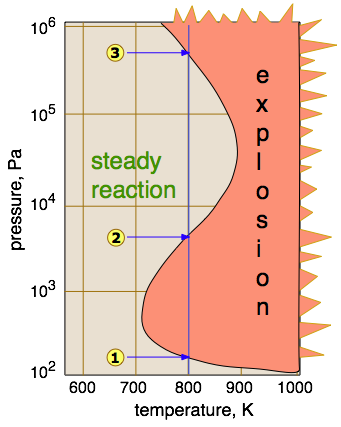
The lower explosion limit of gas mixtures varies with the size, shape, and composition of the enclosing container. Needless to say, experimental determination of explosion limits requires some care and creativity. Upper and lower explosion limits for several common fuel gases are shown below.