Mass Action Law
- Page ID
- 35697
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Identify a system, an open system, a closed system and the environment of the system.
- Define a state of equilibrium.
- Describe the mass action law.
- Apply the mass action law to write expressions for equilibrium constants.
- Write the equilibrium constant expression for any reaction equation.
Heat is energy flowing from a high temperature object to a low temperature object. When the two objects are at the same temperature, there is no net flow of energy or heat. That is why a covered cup of coffee will not be colder than or warmer than the room temperature after it has been in there for a few hours. This phenomenon is known as equilibrium. In this example, we deal with the flow of energy.
Equilibria happen in phase transitions. For example, if the temperature in a system containing a mixture of ice and water is uniformly 273.15 K, the net amount of ice formed and melted will be zero. The amount of liquid water will also remain constant, if no vapor escapes from the system. In this case, three phases, ice (solid) water (liquid), and vapor (gas) are in equilibrium with one another. Similarly, equilibrium can also be established between the vapor phase and the liquid at a particular temperature. Equilibrium conditions also exist between solid phase and vapor phases. These are phase equilibria.
Chemical reactions may not be as complete as we have assumed in Stoichiometry calculations. For example, the following reactions are far short of completion.
\[\ce{2 NO2 \rightleftharpoons N2O4}\]
\[\ce{3 H2 + N2 \rightleftharpoons 2 NH3}\]
\[\ce{H2O + CO \rightleftharpoons H2 + CO2}\]
Let us consider only the first reaction in this case. At room temperature, it is impossible to have pure \(\ce{NO2}\) or \(\ce{N2O4}\). However, in a sealed tube (closed system), the ratio
\[\ce{\dfrac{[N2O4]}{[NO2]^2}}\]
is a constant. This phenomenon is known as chemical equilibrium. Such a law of nature is called the law of mass action or mass action law.
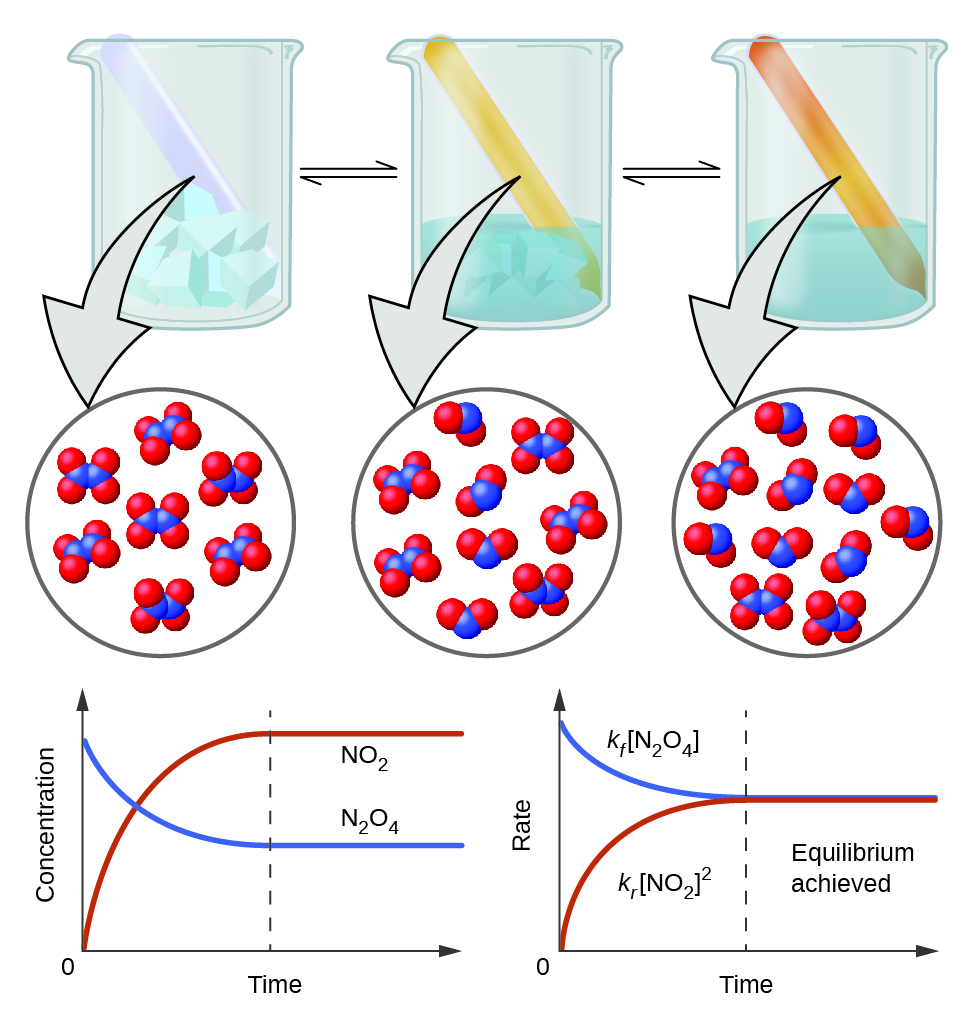
Of course, when conditions, such as pressure and temperature, change, a period of time is required for the system to establish an equilibrium. Before we introduce the mass action law, it is important for us to identify a system or a closed system in our discussion. The law provides an expression for a constant for all reversible reactions. For systems that are not at equilibrium yet, the ratio calculated from the mass action law is called a reaction quotient Q. The Q values of a closed system have a tendency to reach a limiting value called equilibrium constant K over time. A system has a tendency to reach an equilibrium state.
A Closed System for the Equilibrium State
To discuss equilibrium, we must define a system, which may be a cup of water, a balloon, a laboratory, a planet or a universe. Thus, for discussion purposes, we define an isolated portion of the universe under consideration as a system, and anything outside of the system is called environment. When the system under consideration is isolated from its environment in such a way that there is no energy or mass transferred into or out of the system, the system is said to be an isolated system. In a isolated system, changes continue, but eventually there is no NET change over time; such a state is called an equilibrium state.
For example, a glass containing water is an open system. Evaporation lets water molecules escape into the air by absorbing energy from the environment until the glass is empty. When covered and insulated it is a closed system. Water vapor in the space above water eventually reaches an equilibrium vapor pressure. In fact, measuring of temperature itself requires the thermometer to be at the same state as the system it measures. We read the temperature of the thermometer when heat transfer between the thermometer and the system stops (at equilibrium). Equilibrium states are reached for physical as well as chemical reactions. Equilibrium is dynamic in the sense that changes continue, but the net change is zero.
Reversible Chemical Reactions
Heat transfer, vaporization, melting, and other phase changes are physical changes. These changes are reversible and you have already experienced them. Many chemical reactions are also reversible. For example
\[ \underset{colorless}{\ce{N2O4}} \rightleftharpoons \underset{brown}{\ce{2 NO2}}\]
and
\[\ce{N2 + 3 H2 \rightleftharpoons 2 NH3}\]
are reversible chemical reactions.
The Law of Mass Action
The law of mass action is universal, applicable under any circumstance. However, for reactions that are complete, the result may not be very useful. We introduce the mass action law by using a general chemical reaction equation in which reactants \(\ce{A}\) and \(\ce{B}\) react to give products \(\ce{C}\) and \(\ce{D}\).
\[a\, \ce A + b\, \ce B \rightarrow c\, \ce C + d\, \ce D\]
where a, b, c, d are the coefficients for a balanced chemical equation. The mass action law states that if the system is at equilibrium at a given temperature, then the following ratio is a constant:
\[\dfrac{[\ce C]^c [\ce D]^d}{[\ce A]^a [\ce B]^b} = K_{\ce{eq}}\]
The square brackets "[ ]" around the chemical species represent their concentrations. This is the ideal law of chemical equilibrium or law of mass action.
The Reaction Quotient Q vs. the Equilibrium Constants K
If the system is NOT at equilibrium, the ratio is different from the equilibrium constant. In such cases, the ratio is called a reaction quotient which is designated as Q.
\[\dfrac{[\ce C]^c [\ce D]^d}{[\ce A]^a [\ce B]^b} = Q\]
A system not at equilibrium tends to become at equilibrium, and the changes will cause changes in Q so that its value approaches the equilibrium constant, K:
\[Q \rightarrow K_{\ce{eq}}\]
The mass action law gives us a general method to write the expression for the equilibrium constant of any reaction. At this stage, you should be able to write the equilibrium expression for any reaction equation. If you are not sure from the above general theory, here are some examples. It is more important for you to understand WHY the equilibrium constants are expressed this way than what the equilibrium expression is.
Write the the equilibrium constant expression for the reaction equation:
\[\ce{NH3 + HOAc \rightleftharpoons NH4+ + OAc-} \nonumber\]
Hint
\[\ce{\dfrac{[NH4+] [OAc- ]}{[NH3] [HOAc]}} = K\: (\textrm{unitless constant}) \nonumber\]
For the ionization of an acid,
\[\ce{H2SO4 \rightleftharpoons 2 H+ + SO4^2-} \nonumber\]
what is the equilibrium constant expression?
Hint
The equilibrium constant is
\[\ce{\dfrac{[H+]^2 [SO4^2- ]}{[H2SO4]}} = K \ce M^2 \nonumber\]
where M = mol/L. Note the unit for K.
For the reaction equation:
\(\ce{Cu^2+ + 6 NH3 \rightleftharpoons Cu(NH3)6^2+} \nonumber\)
what is the equilibrium constant expression?
Hint
The expression is
\(\ce{\dfrac{[Cu(NH3)6^2+]}{[Cu^2+] [NH3]^6}} = K \ce M^{-6} \nonumber\)
The equilibrium constant depends on the written equation.
Discuss the ionization of oxalic acid, \(\ce{H2C2O4}\), in two stages.
Solution
Experimentally, it has been shown that
\(\ce{H2C2O4 \rightleftharpoons H+ + HC2O4- }\tag{1} \)
\(\ce{\dfrac{[HC2O4- ] [H+]}{[H2C2O4]}} = K_1 = \mathrm{0.059\: M} \nonumber\)
The second ionization constant is much smaller:
\(\ce{HC2O4- \rightleftharpoons H+ + C2O4^2- }\tag{2}\)
\[\ce{\dfrac{[H+] [C2O4^2- ]}{[HC2O4- ]}} = K_2 = \mathrm{0.000064\: M} \nonumber\]
The overall ionization can be obtained by adding (1) and (2) to give (3).
\[\ce{H2C2O4 \rightleftharpoons 2 H+ + C2O4^2- }\tag{3} \nonumber\]
and the equilibrium constant is
\[\ce{\dfrac{[H+]^2 [C2O4^2- ]}{[H2C2O4]}} = K_{3}\: \ce M^2 \nonumber\]
It is obvious that
\[\begin{align*}
K_{3} &= K_1 \times K_2\\
&= 3.8\times10^{-6}\: \ce M^2
\end{align*}\]
Please confirm the above obvious relationship to satisfy yourself.
At some temperature, the equilibrium constant is 4.0 for the reaction
\[\ce{CO_{\large{(g)}} + 3 H_{2\large{(g)}} \rightleftharpoons CH_{4\large{(g)}} + H2O_{\large{(g)}}} \nonumber\]
What is the equilibrium constant expression and value for the reaction,
\[\ce{CH_{4\large{(g)}} + H2O_{\large{(g)}} \rightleftharpoons CO_{\large{(g)}} + 3 H_{2\large{(g)}}}? \nonumber\]
Hint
\(\ce{\dfrac{[CO] [H2]^3}{[CH4] [H2O]}} = \dfrac{1}{4.0} = 0.25\)
At some temperature, the equilibrium constant is 4.0 for the reaction
\(\ce{CO_{\large{(g)}} + 3 H_{2\large{(g)}} \rightleftharpoons CH_{4\large{(g)}} + H2O_{\large{(g)}}}\).
What is the equilibrium constant expression and value for the reaction,
\(\ce{\dfrac{1}{3} CO_{\large{(g)}} + H_{2\large{(g)}} \rightleftharpoons \dfrac{1}{3} CH_{4\large{(g)}} + \dfrac{1}{3} H2O_{\large{(g)}}}\)?
Hint
\(\mathrm{\dfrac{[CH_4]^{1/3} [H_2O]^{1/3}}{[CO]^{1/3} [H_2]} = 4.0^{1/3} = 1.59}\)
The application of the mass action law leads to the method to write the expression for the equilibrium constant. The law is given in a general form, and these examples should help you grasp the method.
Questions
- A closed container has \(\ce{N2O4}\) and \(\ce{NO2}\) gases in it, and it has been placed in the lab for many days. What would you consider the container and the gases to be?
- an open system
- a closed system
- not a system
- A closed container has \(\ce{N2O4}\) and \(\ce{NO2}\) gases in it, and it has been placed in the lab for many days. Is the system at an equilibrium state for the following chemical reaction?
\(\ce{N2O4 \rightleftharpoons 2 NO2}\)
- A closed container has \(\ce{N2O4}\) and \(\ce{NO2}\) gases in it, and it has just been placed in an ice/water bath. Is the system at an equilibrium state for the following chemical reaction?
\(\ce{N2O4 \rightleftharpoons 2 NO2}\)
- \(\ce{HCOOH + CN- \rightleftharpoons HCN + HCOO-}\)
is 5E5, what is the equilibrium constant for the reaction equation
\(\ce{HCN + HCOO- \rightleftharpoons HCOOH + CN-}\)?
- For reactions taking place in the gas phase, the equilibrium constant is normally expressed in terms of partial pressures of the reactants and products. If C represents the concentration, and other symbols of the ideal gas equation are used, which of the following is correct?
- \(C = \dfrac{RT}{PV}\)
- \(C = \dfrac{RT}{P}\)
- \(C = \dfrac{RT}{V}\)
- \(C = \dfrac{RT}{PM}\)
- \(C = \dfrac{P}{RT}\)
- \(C = \dfrac{PV}{RT}\)
- If Kc represents the equilibrium constant in terms of concentration, and Kp represents that in terms of partial pressure, which of the following is correct?
- \(K_c = K_p\)
- \(K_c \propto K_p\)
- \(K_c = \dfrac{1}{K_p}\)
- \(K_c \propto \dfrac{1}{K_p}\)
- \(K_c \times K_p = RT\)
- For which of the following gas-phase reaction equations are the equilibrium constants unitless quantities?
- \(\ce{2 H2 + O2 \rightleftharpoons 2 H2O}\)
- \(\ce{2 NO \rightleftharpoons N2 + O2}\)
- \(\ce{COCl2 \rightleftharpoons CO + Cl2}\)
- \(\ce{CO + H2O \rightleftharpoons CO2 + H2}\)
Solutions
- b
Discussion...
Since it has been in the lab, the temperature of the system is the same as its environment. - yes
Discussion...
Only a few minutes are required for the reaction to reach an equilibrium state. \(\ce{NO2}\) is a brown gas - no
Discussion...
Heat will be extracted from the container, and that causes the equilibrium to shift. At 0 deg C, the equilibrium is shifted to have lots of \(\ce{N2O4}\). - 1/5E5 = 2E-6
Discussion...
Since the reaction equation is reversed, use the relationship\(K_{reverse} = \dfrac{1}{K_{forward}}\).
If you reverse the reaction equation, take the reciprocal of the previous equilibrium constant.
- e
Discussion...
By definition, \(C = \dfrac{n}{V}\). Derive it from \(n R T = P V\). - b
Discussion...
Statements (c), (d), and (e) may be true for special cases, but they are not generally true. In this list, "Kc is proportional to Kp" is true, but a more quantative relationship will be derived. - bd
Discussion...
Both reaction equations in (b) and (d) have equal numbers of reactants and products.
Contributors and Attributions
Chung (Peter) Chieh (Professor Emeritus, Chemistry @ University of Waterloo)

