14.4: Thermochemistry and Calorimetry

Learning Objectives

Make sure you thoroughly understand the following essential concepts:

• Write a balanced thermochemical equation that expresses the enthalpy change for a given chemical reaction. Be sure to correctly specificy the physical state (and, if necessary, the concentration) of each component.
• Write an equation that defines the standard enthalpy of formation of a given chemical species.
• Define the standard enthalpy change of a chemical reaction. Use a table of standard enthalpies of formation to evaluate ΔH_f°.
• State the principle on which Hess' law depends, and explain why this law is so useful.
• Describe a simple calorimeter and explain how it is employed and how its heat capacity is determined.

The heat that flows across the boundaries of a system undergoing a change is a fundamental property that characterizes the process. It is easily measured, and if the process is a chemical reaction carried out at constant pressure, it can also be predicted from the difference between the enthalpies of the products and reactants. The quantitative study and measurement of heat and enthalpy changes is known as thermochemistry.

Thermochemical Equations and Standard States

In order to define the thermochemical properties of a process, it is first necessary to write a thermochemical equation that defines the actual change taking place, both in terms of the formulas of the substances involved and their physical states (temperature, pressure, and whether solid, liquid, or gaseous.

To take a very simple example, here is the complete thermochemical equation for the vaporization of water at its normal boiling point:

\[\ce{H2O(\ell,\, 373 \,K, \,1 \,atm) → H2O(g, \,373 \,K, \,1 \,atm)} \,\,\,ΔH = 40.7\, kJ\, mol^{-1} \nonumber\]

The quantity 40.7 is known as the enthalpy of vaporization (often referred to as “heat of vaporization”) of liquid water. The following points should be kept in mind when writing thermochemical equations:

Any thermodynamic quantity such as \(ΔH\) that is associated with a thermochemical equation always refers to the number of moles of substances explicitly shown in the equation. Thus for the synthesis of water we can write

\[\ce{2 H2(g) + O2(g)→ 2 H2O(l) }\,\,\,ΔH = -572 \,kJ \nonumber\]

or

\[\ce{H2(g) + 1/2 O2(g)→ H2O(l)} \,\,\, ΔH = -286 \,kJ \nonumber\]

The thermochemical equations for reactions taking place in solution must also specify the concentrations of the dissolved species. For example, the enthalpy of neutralization of a strong acid by a strong base is given by

\[\ce{H^{+}(aq,\, 1M,\, 298\, K,\, 1\, atm) + OH^{-} (aq,\, 1M,\, 298 \,K,\, 1 \,atm) → H2O(\ell, 373\, K,\, 1 \,atm) } \,\,\, ΔH = -56.9\, kJ\, mol^{-1} \nonumber\]

in which the abbreviation aq refers to the hydrated ions as they exist in aqueous solution. Since most thermochemical equations are written for the standard conditions of 298 K and 1 atm pressure, we can leave these quantities out if these conditions apply both before and after the reaction. If, under these same conditions, the substance is in its preferred (most stable) physical state, then the substance is said to be in its standard state.

Thus the standard state of water at 1 atm is the solid below 0°C, and the gas above 100°C. A thermochemical quantity such as \(ΔH\) that refers to reactants and products in their standard states is denoted by \(ΔH^°\).

Concentrations vs. Effective Concentrations (Activities)

In the case of dissolved substances, the standard state of a solute is that in which the “effective concentration”, known as the activity, is unity. For non-ionic solutes the activity and molarity are usually about the same for concentrations up to about 1M, but for an ionic solute this approximation is generally valid only for solutions more dilute than 0.001-0.01M, depending on electric charge and size of the particular ion.

Standard Enthalpy of Formation

The enthalpy change for a chemical reaction is the difference

\[ΔH = H_{products} - H_{reactants}\]

If the reaction in question represents the formation of one mole of the compound from its elements in their standard states, as in

\[\ce{H2(g) + 1/2O2(g) -> H2O(l)} \;\;\; ΔH = -286\; kJ\]

then we can arbitrarily set the enthalpy of the elements to zero and write

\[\begin{align*} H_f^o &= \sum H_f^o (products) - \sum H_f^o (reactants) \\[4pt] &= -286\; kJ - 0 \\[4pt] &= -268\; kJ \,mol^{-1} \end{align*}\]

which defines the standard enthalpy of formation of water at 298 K. The value H_f ° = -268 kJ tells us that when hydrogen and oxygen, each at a pressure of 1 atm and at 298 K (25° C) react to form 1 mole of liquid water also at 25°C and 1 atm pressure, 268 kJ will have passed from the system (the reaction mixture) into the surroundings. The negative sign indicates that the reaction is exothermic: the enthalpy of the product is smaller than that of the reactants. The standard enthalpy of formation is a fundamental property of any compound. Table T1 list H_f ° values (usually alongside values of other thermodynamic properties) in their appendices.

The standard enthalpy of formation of a compound is defined as the heat associated with the formation of one mole of the compound from its elements in their standard states.

In general, the standard enthalpy change for a reaction is given by the expression

\[ΔH_f^o= \sum H_f^o (products) - \sum H_f^o (reactants) \label{2-1}\]

in which the \(\sum H_f^o\) terms indicate the sums of the standard enthalpies of formations of all products and reactants. The above definition is one of the most important in chemistry because it allows us to predict the enthalpy change of any reaction without knowing any more than the standard enthalpies of formation of the products and reactants, which are widely available in tables.

The following examples illustrate some important aspects of the standard enthalpy of formation of substances.

Molarity

The thermochemical equation defining \(H_f^o\) is always written in terms of one mole of the substance in question> For example, the relavante thermodynamic equation for the heat of formation of ammonia (\(\ce{NH3}\)) is:

\[\ce{ 1/2 N2(g) + 3/2 H2(g)→ NH3(g)}\,\,\, ΔH^o = -46.1\, kJ \,(\text{per mole of } \ce{NH3}) \nonumber\]

Allotropes

The standard heat of formation of a compound is always taken in reference to the forms of the elements that are most stable at 25°C and 1 atm pressure.

A number of elements, of which sulfur and carbon are common examples, can exist in more then one solid crystalline form (called allotropes). For carbon dixoide (\(ce{CO2}\), one can construct two thermodynamics equations:

\[\ce{C(graphite) + O2(g) → CO2(g)}\,\,\, ΔH^o ≡ H_f^o = -393.5\, kJ\, mol^{-1} \nonumber\]

\[\ce{C(diamond) + O2(g) → CO2(g)}\,\,\, ΔH^{o} = -395.8\, kJ\, mol^{-1} \nonumber\]

However for carbon, the graphite form is the more stable form and the correct thermodynamic equations for the heat of formation.

Heats of Vaporization

The physical state of the product of the formation reaction must be indicated explicitly if it is not the most stable one at 25°C and 1 atm pressure:

\[\ce{H2(g) + 1/2 O2(g) → H2O(aq)}\,\,\, ΔH^o ≡ H_f^o = -285.8\, kJ\, mol^{-1} \nonumber\]

\[\ce{H2(g) + 1/2 O2(g) → H2O(g)} \,\,\, ΔH^o = -241.8\, kJ\, mol^{-1} \nonumber\]

Notice that the difference between these two \(ΔH^o\) values is just the heat of vaporization of water.

Endothermic Heats of Formation

Although the formation of most molecules from their elements is an exothermic process, the formation of some compounds is mildly endothermic:

\[\ce{1/2 N2(g) + O2(g) -> NO2(g)}\,\,\, ΔH^o ≡ H_f^° = +33.2\, kJ\, mol^{-1} \nonumber\]

A positive heat of formation is frequently associated with instability— the tendency of a molecule to decompose into its elements, although it is not in itself a sufficient cause. In many cases, however, the rate of this decomposition is essentially zero, so it is still possible for the substance to exist. In this connection, it is worth noting that all molecules will become unstable at higher temperatures.

Non-Existing Compounds

The thermochemical reactions that define the heats of formation of most compounds cannot actually take place. For example, the direct synthesis of methane from its elements

\[\ce{C(graphite) + 2 H2(g) → CH4(g)} \nonumber\]

cannot be observed directly owing to the large number of other possible reactions between these two elements. However, the standard enthalpy change for such a reaction be found indirectly from other data, as explained in the next section.

Heats of Atomization

The standard enthalpy of formation of gaseous atoms from the element is known as the heat of atomization.

Heats of atomization are always positive, and are important in the calculation of bond energies.

\[\ce{Fe(s) → Fe(g)}\,\, ΔH° = 417 \,kJ\, mol^{-1} \nonumber\]

Ions in Solution

The standard enthalpy of formation of an ion dissolved in water is expressed on a separate scale in which that of \(\ce{H^{+}(aq)}\) is defined as zero.

The standard heat of formation of a dissolved ion such as \(\ce{Cl^{-}(aq)}\) (that is, formation of the ion from the element) cannot be measured because it is impossible to have a solution containing a single kind of ion. For this reason, ionic enthalpies are expressed on a separate scale on which \(\ce{H_f^o}\) of the hydrogen ion at unit activity (1 M effective concentration) is defined as zero:

\[\ce{1/2 H2(g) → H^{+}(aq)}\,\,\, ΔH^o ≡ H_f^o = 0\, kJ\, mol^{-1} \nonumber\]

Other ionic enthalpies (as they are commonly known) are found by combining appropriate thermochemical equations (as explained in Section 3 below). For example, H_f° of HCl(aq) is found from the enthalpies of formation and solution of HCl(g), yielding

\[\ce{1/2 H2(g) + 1/2 Cl2(g) → HCl(aq)}\,\,\,\ ΔH^o ≡ H_f^o = -167\, kJ\, mol^{-1} \nonumber\]

Because H_f° for H⁺(aq) is zero, this value establishes the standard enthalpy of the chloride ion. The standard enthalpy of formation of Ca²⁺(aq), given by

\[\ce{Ca(s) + Cl2(g) -> CaCl2(aq)} \nonumber\]

could then be calculated by combining other measurable quantities such as the enthalpies of formation and solution of \(\ce{CaCl2(s)}\) to find H_f° for CaCl₂(aq), from which H_f° of \(\ce{Ca^{2+}(aq)}\) is found by difference from that of \(\ce{Cl^{-}(aq)}\). Tables of the resulting ionic enthalpies are widely available (see here).

Hess’ Law and Thermochemical Calculations

Two or more chemical equations can be combined algebraically to give a new equation. Even before the science of thermodynamics developed in the late nineteenth century, it was observed that the heats associated with chemical reactions can be combined in the same way to yield the heat of another reaction. For example, the standard enthalpy changes for the oxidation of graphite and diamond can be combined to obtain ΔH° for the transformation between these two forms of solid carbon, a reaction that cannot be studied experimentally.

\[\ce{C(graphite) + O2(g)→ CO2(g)}\,\,\, ΔH^o = -393.51\, kJ\, mol^{-1}\]

\[\ce{C(diamond) + O2(g)→ CO2(g)} \,\,\, ΔH^o = -395.40\, kJ\, mol^{-1}\]

Subtraction of the second reaction from the first (i.e., writing the second equation in reverse and adding it to the first one) yields

\[\ce{C(graphite) → C(diamond)}\,\,\, ΔH^{°} = 1.89\, kJ\, mol^{-1}\]

This principle, known as Hess’ law of independent heat summation is a direct consequence of the enthalpy being a state function. Hess’ law is one of the most powerful tools of chemistry, for it allows the change in the enthalpy (and in other thermodynamic functions) of huge numbers of chemical reactions to be predicted from a relatively small base of experimental data.

Germain Henri Hess

Germain Henri Hess (1802-1850) was a Swiss-born professor of chemistry at St. Petersburg, Russia. He formulated his famous law, which he discovered empirically, in 1840. Very little appears to be known about his other work in chemistry.

Standard Enthalpies of Combustion

Because most substances cannot be prepared directly from their elements, heats of formation of compounds are seldom determined by direct measurement. Instead, Hess’ law is employed to calculate enthalpies of formation from more accessible data. The most important of these are the standard enthalpies of combustion. Most elements and compounds combine with oxygen, and many of these oxidations are highly exothermic, making the measurement of their heats relatively easy. For example, by combining the heats of combustion of carbon, hydrogen, and methane, we can obtain the standard enthalpy of formation of methane, which as we noted above, cannot be determined directly (Example \(\PageIndex{1}\)).

Example \(\PageIndex{1}\): Combustion of Methane

Use the following heat of formation/combustion information to estimate the standard heat of formation of methane \(\ce{CH4}\).

\[\begin{aligned} \ce{C(graphite)} + \ce{O2(g)} &→ \ce{CO2(g)} \quad &ΔH° = -393\, kJ\, mol^{-1} \label{P1-1} \\[4pt] \ce{H2(g)} + \ce{1/2 O2(g)} &→ \ce{H2O(g)} \quad &ΔH° = -286 kJ mol^{-1} \label{P1-2} \\[4pt] \ce{CH4(g)} + \ce{2O2(g)} &→ \ce{CO2(g)} + \ce{2H2O(g)} \quad &ΔH^o = -890\, kJ\, mol^{-1} \label{P1-3} \end{aligned}\]

Solution

The standard heat of formation of methane is defined by the reaction

\[\ce{C(graphite) + 2H2(g) → CH4(g)} \quad ΔH^o = ? \label{P1-4}\]

Our task is thus to combine the top three equations in such a way that they add up to (4).

Step 1

Begin by noting that (3), the combustion of methane, is the only equation that contains the CH₄ term, so we need to write it in reverse (not forgetting to reverse the sign of ΔH°!) so that CH₄ appears as the product.

\[\ce{CO2(g) + 2H2O(g) → CH4(g) + 2O2(g)} \quad ΔH^o = +890\, kJ\, mol^{-1} \label{P1-3Rev}\]

Step 2

Since H₂O does not appear in the net reaction (4), add two times (2) to cancel these out. Notice that this also cancels one of the oxygens in (3Rev):

CO₂(g) + 2H₂O(g) → CH₄(g) + 2O₂(g) ΔH° = +890 kJ mol^-1(P1-3Rev)
→ 2H₂O(g) ΔH° = -484 kJ mol^-1(P1-2)

Step 3

Finally, get rid of the remaining O₂ and CO₂ by adding (1); this also adds a needed C:

→ CH₄(g) + 2O₂(g) ΔH° = +890 kJ mol^-1(P1-3Rev)
→ 2H₂O(g) ΔH° = -572 kJ mol^-1(P1-2)
→ CO₂(g) ΔH° = -393 kJ mol^-1(P1-1)

Step 4

So our creative cancelling has eliminated all except the substances that appear in (4). Just add up the enthalpy changes and we are done:

\[\ce{C(graphite) + 2H2(g) → CH4(g)} \]

(The tablulated value is -74.6 kJ mol^-1)

Calorimetry: Measuring ΔH in the laboratory

How are enthalpy changes determined experimentally? First, you must understand that the only thermal quantity that can be observed directly is the heat q that flows into or out of a reaction vessel, and that q is numerically equal to ΔH° only under the special condition of constant pressure. Moreover, q is equal to the standard enthalpy change only when the reactants and products are both at the same temperature, normally 25°C. The measurement of q is generally known as calorimetry.

The most common types of calorimeters contain a known quantity of water which absorbs the heat released by the reaction. Because the specific heat capacity of water (4.184 J g^-1 K^-1) is known to high precision, a measurement of its temperature rise due to the reaction enables one to calculate the quantity of heat released.

In all but the very simplest calorimeters, some of the heat released by the reaction is absorbed by the components of the calorimeter itself. It is therefore necessary to "calibrate" the calorimeter by measuring the temperature change that results from the introduction of a known quantity of heat. The resulting calorimeter constant, expressed in J K^-1, can be regarded as the “heat capacity of the calorimeter”. The known source of heat is usually produced by passing a known quantity of electric current through a resistor within the calorimeter, but it can be measured by other means as described in the following problem example.

Example \(\PageIndex{2}\): Heat Capacity of a Calorimeter

In determining the heat capacity of a calorimeter, a student mixes 100.0 g of water at 57.0 °C with 100.0 g of water, already in the calorimeter, at 24.2°C. (yhe specific heat of water is 4.184 J g^-1 K^-1). After mixing and thermal equilibration with the calorimeter, the temperature of the water stabilizes at 38.7°C. Calculate the heat capacity of the calorimeter in J/K.

Solution

The hot water loses heat, the cold water gains heat, and the calorimter itself gains heat, so this is essentially a thermal balance problem. Conservation of energy requires that

\[q_{hot} + q_{cold} + q_{cal} = 0 \nonumber\]

We can evaluate the first two terms from the observed temperature changes:

\[q_{hot} = (100\; g) (38.7\;K - 57.0\;K) (4.184\; J \;g^{-1}K^{-1}) = -7,657\; J \nonumber\]

\[q_{cold} = (100\; g) (38.7 \;K - 24.2 \;K) (4.184\; J\; g^{-1} K^{-1}) = 6,067\; J \nonumber\]

So

\[q_{cal} = 7,657 \;J - ,6067\; J = 1,590;\ J \nonumber\]

The calorimeter constant is

\[\dfrac{1590\; J}{38.7\; K - 24.2\; K} = 110\; J\; K^{-1} \nonumber\]

Note: Strictly speaking, there is a fourth thermal balance term that must be considered in a highly accurate calculation: the water in the calorimeter expands as it is heated, performing work on the atmosphere.

For reactions that can be initiated by combining two solutions, the temperature rise of the solution itself can provide an approximate value of the reaction enthalpy if we assume that the heat capacity of the solution is close to that of the pure water — which will be nearly true if the solutions are dilute.

For example, a very simple calorimetric determination of the standard enthalpy of the reaction

\[\ce{H^{+}(aq) + OH^{-}(aq) → H2O(\ell)} \nonumber\]

could be carried out by combining equal volumes of 0.1M solutions of HCl and of NaOH initially at 25°C. Since this reaction is exothermic, a quantity of heat q will be released into the solution. From the temperature rise and the specific heat of water, we obtain the number of joules of heat released into each gram of the solution, and q can then be calculated from the mass of the solution. Since the entire process is carried out at constant pressure, we have ΔH° = q.

For reactions that cannot be carried out in dilute aqueous solution, the reaction vessel is commonly placed within a larger insulated container of water. During the reaction, heat passes between the inner and outer containers until their temperatures become identical. Again, the temperature change of the water is observed, but in this case we need to know the value of the calorimeter constant described above.

The Bomb Calorimeter

\(\Delta H_{combustion}\), since these are essential to the determination of standard enthalpies of formation of the thousands of new compounds that are prepared and characterized each month. In a constant volume calorimeter, the system is sealed or isolated from its surroundings, and this accounts for why its volume is fixed and there is no volume-pressure work done. A bomb calorimeter structure consists of the following:

• Steel bomb which contains the reactants
• Water bath in which the bomb is submerged
• Thermometer
• A motorized stirrer
• Wire for ignition

Figure 1: A simplified bomb calorimeter

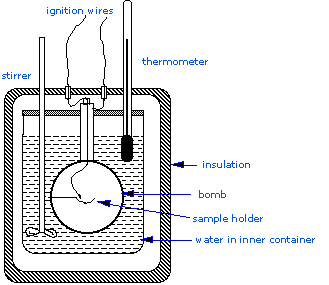
Since the process takes place at constant volume, the reaction vessel must be constructed to withstand the high pressure resulting from the combustion process, which amounts to a confined explosion. The vessel is usually called a “bomb”, and the technique is known as bomb calorimetry. The reaction is initiated by discharging a capacitor through a thin wire which ignites the mixture.

Another consequence of the constant-volume condition is that the heat released corresponds to q_v , and thus to the internal energy change ΔU rather than to ΔH. The enthalpy change is calculated according to the formula

\[ΔH = q_v + Δn_gRT\]

• \(Δn_g\)  is the change in the number of moles of gases in the reaction.

Example \(\PageIndex{3}\): Combustion of Biphenyl

A sample of biphenyl (C₆H₅)₂ weighing 0.526 g was ignited in a bomb calorimeter initially at 25°C, producing a temperature rise of 1.91 K. In a separate calibration experiment, a sample of benzoic acid C₆H₅COOH weighing 0.825 g was ignited under identical conditions and produced a temperature rise of 1.94 K. For benzoic acid, the heat of combustion at constant pressure is known to be 3226 kJ mol^-1 (that is, ΔU = -3226 kJ mol^-1.) Use this information to determine the standard enthalpy of combustion of biphenyl.

Solution

Begin by working out the calorimeter constant:

• Moles of benzoic acid:

\[\dfrac{(0.825 g}{122.1 \;g/mol} = 0.00676\; mol\nonumber\]

• Heat released to calorimeter:

\[(0.00676\; mol) \times (3226\; kJ/mol) = 21.80\; kJ\nonumber\]

• Calorimeter constant:

\[\dfrac{21.80\; kJ}{1.94\; K} = 11.24\; kJ/K\nonumber\]

Now determine \(ΔU_{combustion}\) of the biphenyl ("BP"):

• moles of biphenyl:

\[\dfrac{0.526\; g}{154.12\; g/mol} = 0.00341 \; mol\nonumber\]

• heat released to calorimeter:

\[(1.91\; K) \times (11.24\; kJ/K) = 21.46\; kJ\nonumber\]

• heat released per mole of biphenyl:

\[\dfrac{21.46\; kJ}{0.00341\; mol} = 6,293\; kJ/mol\nonumber\]

\[ΔU_{combustion} (BP) = -6,293\; kJ/mol\nonumber\]

(This is the heat change at constant volume, \(q_v\); the negative sign indicates that the reaction is exothermic, as all combustion reactions are.)

From the reaction equation

\[(C_6H_5)_{2(s)} + \frac{19}{2} O_{2(g)} \rightarrow 12 CO_{2(g)} + 5 H_2O_{(l)} \nonumber\]

we have

\[Δn_g = 12 - \frac{19}{2} = \frac{-5}{2} \nonumber\]

Thus the volume of the system decreases when the reaction takes place. Converting to ΔH, we can write the following equation. Additionally, recall that at constant volume, \(ΔU = q_V\).

\[\begin{align*} ΔH &= q_V + Δn_gRT \\[4pt] &= ΔU -\left( \dfrac{5}{2}\right) (8.314\; J\; mol^{-1}\; K^{-1}) (298 \;K) \\[4pt] &=(-6,293 \; kJ/mol)-(6,194\; J/mol)=(-6,293-6.2)\;kJ/mol= -6299 \; kJ/mol \end{align*}\]

A common mistake here is to forget that the subtracted term is in J, not kJ. Note that the additional 6.2 kJ in \(ΔH\) compared to \(ΔU\) reflects the work that the surroundings do on the system as the volume of gases decreases according to the reaction equation.

Determining the Heat of Reaction

The amount of heat that the system gives up to its surroundings so that it can return to its initial temperature is the heat of reaction. The heat of reaction is just the negative of the thermal energy gained by the calorimeter and its contents (\(q_{calorimeter}\)) through the combustion reaction.

\[q_{rxn} = -q_{calorimeter} \label{2A}\]

where

\[q_{calorimeter} = q_{bomb} + q_{water} \label{3A}\]

If the constant volume calorimeter is set up the same way as before, (same steel bomb, same amount of water, etc.) then the heat capacity of the calorimeter can be measured using the following formula:

\[q_{calorimeter} = \text{( heat capacity of calorimeter)} \times \Delta{T} \label{4A}\]

Heat capacity is defined as the amount of heat needed to increase the temperature of the entire calorimeter by 1 °C. The equation above can also be used to calculate \(q_{rxn}\) from \(q_{calorimeter}\) calculated by Equation 2. The heat capacity of the calorimeter can be determined by conducting an experiment.

Example \(\PageIndex{4}\): Heat of Combustion

1.150 g of sucrose goes through combustion in a bomb calorimeter. If the temperature rose from 23.42°C to 27.64°C and the heat capacity of the calorimeter is 4.90 kJ/°C, then determine the heat of combustion of sucrose, \(C_{12}H_{22}O_{11}\), in kJ per mole of \(C_{12}H_{22}O_{11}\).

Given:

• mass of \(C_{12}H_{22}O_{11}\): 1.150 g
• \(T_{initial}\): 23.42°C
• \(T_{final}\):27.64°C
• Heat Capacity of Calorimeter: 4.90 kJ/°C

Solution

Using Equation 4 to calculate \(q_{calorimeter}\):

\[q_{calorimeter} = (4.90\; kJ/°C) \times (27.64 - 23.42)°C = (4.90 \times 4.22) \;kJ = 20.7\; kJ \]

Plug into Equation 2:

\(q_{rxn} = -q_{calorimeter} = -20.7 \; kJ \;\)

But the question asks for kJ/mol \(C_{12}H_{22}O_{11}\), so this needs to be converted:

\(q_{rxn} = \dfrac{-20.7 \; kJ}{1.150 \; g \; C_{12}H_{22}O_{11}} = \dfrac{-18.0 \; kJ}{g\; C_{12}H_{22}O_{11}}\)

Per Mole \(C_{12}H_{22}O_{11}\):

\(q_{rxn} = \dfrac{-18.0 \; kJ}{g \; C_{12}H_{22}O_{11}} \times \dfrac{342.3 \; g \; C_{12}H_{22}O_{11}}{1 \; mol \; C_{12}H_{22}O_{11}} = \dfrac{-6.16 \times 10^3 \; kJ \;}{mol \; C_{12}H_{22}O_{11}}\)

Calorimeters

Although calorimetry is simple in principle, its practice is a highly exacting art, especially when applied to processes that take place slowly or involve very small heat changes, such as the germination of seeds. Calorimeters can be as simple as a foam plastic coffee cup, which is often used in student laboratories. Research-grade calorimeters, able to detect minute temperature changes, are more likely to occupy table tops, or even entire rooms:

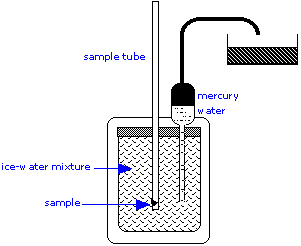
The ice calorimeter is an important tool for measuring the heat capacities of liquids and solids, as well as the heats of certain reactions. This simple yet ingenious apparatus is essentially a device for measuring the change in volume due to melting of ice. To measure a heat capacity, a warm sample is placed in the inner compartment, which is surrounded by a mixture of ice and water.

The heat withdrawn from the sample as it cools causes some of the ice to melt. Since ice is less dense than water, the volume of water in the insulated chamber decreases. This causes an equivalent volume of mercury to be sucked into the inner reservoir from the outside container. The loss in weight of this container gives the decrease in volume of the water, and thus the mass of ice melted. This, combined with the heat of fusion of ice, gives the quantity of heat lost by the sample as it cools to 0°C.