14.3: Molecules as Energy Carriers and Converters

Learning Objectives

Make sure you thoroughly understand the following essential concepts:

• Describe the sources of potential energy and kinetic energy contained in a molecule.
• Describe the nature of "thermal" energy, and how it relates to other forms of kinetic energy and to temperature.
• Explain why the simplest molecules (monatomic and diatomic) have smaller heat capacities than polyatomic molecules.
• Similarly, explain why the dependence of heat capacity on the temperature is different for monatomic and polyatomic molecules.

All molecules at temperatures above absolue zero possess thermal energy— the randomized kinetic energy associated with the various motions the molecules as a whole, and also the atoms within them, can undergo. Polyatomic molecules also possess potential energy in the form of chemical bonds. Molecules are thus both vehicles for storing and transporting energy, and the means of converting it from one form to another when the formation, breaking, or rearrangement of the chemical bonds within them is accompanied by the uptake or release of heat.

Chemical Energy: Potential + Kinetic

When you buy a liter of gasoline for your car, a cubic meter of natural gas to heat your home, or a small battery for your flashlight, you are purchasing energy in a chemical form. In each case, some kind of a chemical change will have to occur before this energy can be released and utilized: the fuel must be burned in the presence of oxygen, or the two poles of the battery must be connected through an external circuit (thereby initiating a chemical reaction inside the battery.) And eventually, when each of these reactions is complete, our source of energy will be exhausted; the fuel will be used up, or the battery will be “dead”.

Where did the energy go? It could have gone to raise the temperature of the products, to perform work in expanding any gaseous products or to push electrons through a circuit. The remainder will reside in the chemical potential energy associated with the products of the reaction.

Chemical substances are made of atoms, or more generally, of positively charged nuclei surrounded by negatively charged electrons. A molecule such as dihydrogen, H₂, is held together by electrostatic attractions mediated by the electrons shared between the two nuclei. The total potential energy of the molecule is the sum of the repulsions between like charges and the attractions between electrons and nuclei:

\[PE_{total} = PE_{electron-electron} + PE_{nucleus-nucleus} + PE_{nucleus-electron} \label{1-1}\]

In other words, the potential energy of a molecule depends on the time-averaged relative locations of its constituent nuclei and electrons. This dependence is expressed by the familiar potential energy curve which serves as an important description of the chemical bond between two atoms.

Translation refers to movement of an object as a complete unit. Translational motions of molecules in solids or liquids are restricted to very short distances comparable to the dimensions of the molecules themselves, whereas in gases the molecules typically travel hundreds of molecular diameters between collisions.

In gaseous hydrogen, for example, the molecules will be moving freely from one location to another; this is called translational motion, and the molecules therefore possess translational kinetic energy

\[KE_{trans} = \dfrac{mv^2}{2}\]

in which \(v\) stands for the average velocity of the molecules; you may recall from your study of gases that \(v\), and therefore \(KE_{trans}\), depends on the temperature.

In addition to translation, molecules composed of two or more atoms can possess other kinds of motion. Because a chemical bond acts as a kind of spring, the two atoms in H₂ will have a natural vibrational frequency. In more complicated molecules, many different modes of vibration become possible, and these all contribute a vibrational term KE_vib to the total kinetic energy. Finally, a molecule can undergo rotational motions which give rise to a third term \(KE_{rot}\). Thus the total kinetic energy of a molecule is the sum

\[KE_{total} = KE_{trans} + KE_{vib} + KE_{rot} \label{1-2}\]

The total energy of the molecule (its internal energy U) is just the sum

\[U = KE_{total} + PE_{total} \label{1-3}\]

Although this formula is simple and straightforward, it cannot take us very far in understanding and predicting the behavior of even one molecule, let alone a large number of them. The reason, of course, is the chaotic and unpredictable nature of molecular motion. Fortunately, the behavior of a large collection of molecules, like that of a large population of people, can be described by statistical methods.

How Molecules Store Thermal Energy

As noted above, the heat capacity of a substance is a measure of how sensitively its temperature is affected by a change in heat content; the greater the heat capacity, the less effect a given flow of heat q will have on the temperature.

Thermal energy is randomized kinetic energy

We also pointed out that temperature is a measure of the average kinetic energy due to translational motions of molecules. If vibrational or rotational motions are also active, these will also accept thermal energy and reduce the amount that goes into translational motions. Because the temperature depends only on the latter, the effect of the other kinds of motions will be to reduce the dependence of the internal energy on the temperature, thus raising the heat capacity of a substance.

Table \(\PageIndex{1}\): Molar heat capacities (kJ mol^–1 K^–1) of some gaseous substances at constant pressure.

monatomic		diatomic		triatomic
He	20.5	CO	29.3	H2O	33.5
Ne	20.5	N2	29.5	D2O	34.3
Ar	20.5	F2	31.4	CO2	37.2
Kr	20.5	Cl2	33.9	CS2	45.6

Whereas monatomic molecules can only possess translational thermal energy, two additional kinds of motions become possible in polyatomic molecules.

A linear molecule has an axis that defines two perpendicular directions in which rotations can occur; each represents an additional degree of freedom, so the two together contribute a total of ½ R to the heat capacity.

Vibrational and rotational motions are not possible for monatomic species such as the noble gas elements, so these substances have the lowest heat capacities. Moreover, as you can see in the leftmost column of Table 1, their heat capacities are all the same. This reflects the fact that translational motions are the same for all particles; all such motions can be resolved into three directions in space, each contributing one degree of freedom to the molecule and ½ R to its heat capacity. (R is the gas constant, 8.314 J K^–₁).

Think of a "degree of freedom" as a kind of motion that adds kinetic energy to a molecule.

For a non-linear molecule, rotations are possible along all three directions of space, so these molecules have a rotational heat capacity of 3/2 R. Finally, the individual atoms within a molecule can move relative to each other, producing a vibrational motion. A molecule consisting of N atoms can vibrate in 3N –6 different ways or modes. Each vibrational mode contributes R (rather than ½ R) to the total heat capacity. (These results come from advanced mechanics and will not be proven here.)

Table \(\PageIndex{2}\): Contribution of molecular motions to heat capacity

type of motion →	translation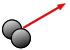	rotation	vibration
monatomic	3/2R	0	0
diatomic	3/2 R	R	R
polyatomic	3/2 R	3/2 R	3N – 6
separation between adjacent levels, (kJ mol^–1)	6.0 × 10^–17 J (O2)	373 J (HCl)	373 J (HCl)

Monatomic molecules have the smallest heat capacities

Now we are in a position to understand why more complicated molecules have higher heat capacities. The total kinetic energy of a molecule is the sum of those due to the various kinds of motions:

\[KE_{total} = KE_{trans} + KE_{rot} + KE_{vib} \label{2-1}\]

When a monatomic gas absorbs heat, all of the energy ends up in translational motion, and thus goes to increase its temperature. In a polyatomic gas, by contrast, the absorbed energy is partitioned among the other kinds of motions; since only the translational motions contribute to the temperature, the temperature rise is smaller, and thus the heat capacity is larger. There is one very significant complication, however: classical mechanics predicts that the energy is always partitioned equally between all degrees of freedom. Experiments, however, show that this is observed only at quite high temperatures. The reason is that these motions are all quantized. This means that only certain increments of energy are possible for each mode of motion, and unless a certain minimum amount of energy is available, a given mode will not be active at all and will contribute nothing to the heat capacity.

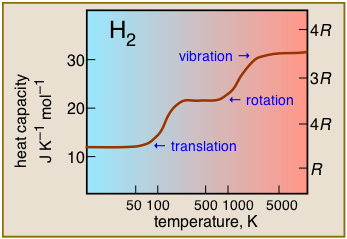
Translational energy levels are effectively a continuum

The shading indicates the average thermal energy available at 300 K. Only those levels within this range will have significant occupancy as indicated by the thickness of the lines in the two rightmost columns. At 300 K, only the lowest vibrational state and the first few rotational states will be active. Most of the thermal energy will be confined to the translational levels whose minute spacing (10^–17 J) causes them to appear as a continuum.

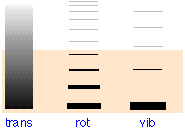
Heat capacity of dihydrogen as a function of temperature. This plot is typical of those for other polyatomic molecules, and shows the practical consequences of the spacings of the various forms of thermal energy. Thus translational motions are available at virtually all temperatures, but contributions to heat acapacity by rotational or vibrational motions can only develop at temperatures sufficiently large to excite these motions.

It turns out that translational energy levels are spaced so closely that they these motions are active almost down to absolute zero, so all gases possess a heat capacity of at least 3/2 R at all temperatures. Rotational motions do not get started until intermediate temperatures, typically 300-500K, so within this range heat capacities begin to increase with temperature. Finally, at very high temperatures, vibrations begin to make a significant contribution to the heat capacity

The strong intermolecular forces of liquids and many solids allow heat to be channeled into vibrational motions involving more than a single molecule, further increasing heat capacities. One of the well known “anomalous” properties of liquid water is its high heat capacity (75 J mol^–1 K^–1) due to intermolecular hydrogen bonding, which is directly responsible for the moderating influence of large bodies of water on coastal climates.

Heat capacities of metals

Metallic solids are a rather special case. In metals, the atoms oscillate about their equilibrium positions in a rather uniform way which is essentially the same for all metals, so they should all have about the same heat capacity. That this is indeed the case is embodied in the Law of Dulong and Petit. In the 19th century these workers discovered that the molar heat capacities of all the metallic elements they studied were around to 25 J mol^–1 K^–1, which is close to what classical physics predicts for crystalline metals. This observation played an important role in characterizing new elements, for it provided a means of estimating their molar masses by a simple heat capacity measurement.

Standard enthalpy change

Under the special conditions in which the pressure is 1 atm and the reactants and products are at a temperature of 298 K, ΔH becomes the standard enthalpy change ΔH°. Chemists usually refer to the "enthalpy change of a reaction" as simply the "enthalpy of reaction", or even more simply as the "heat of reaction". But students are allowed to employ this latter shortcut only if they are able to prove that they know the meaning of enthalpy.

Since most changes that occur in the laboratory, on the surface of the earth, and in organisms are subjected to an approximately constant pressure of "one atmosphere" and reasonably salubrious temperatures, most reaction heats quoted in the literature refer to ΔH°. But the high pressures and extreme temperatures frequently encountered by chemical engineers, geochemists, and practicioners of chemical oceanography, often preclude the convenience of the "standard" values.

The rearrangement of atoms that occurs in a chemical reaction is virtually always accompanied by the liberation or absorption of heat. If the purpose of the reaction is to serve as a source of heat, such as in the combustion of a fuel, then these heat effects are of direct and obvious interest. We will soon see, however, that a study of the energetics of chemical reactions in general can lead us to a deeper understanding of chemical equilibrium and the basis of chemical change itself.

In chemical thermodynamics, we define the zero of the enthalpy and internal energy as that of the elements as they exist in their stable forms at 298K and 1 atm pressure. Thus the enthalpies H of Xe(g), O₂(g) and C(diamond) are all zero, as are those of H₂ and Cl₂ in the reaction

\[H_{2(g)} + Cl_{2(g)} → 2 HCl_{(g)}\]

The enthalpy of two moles of HCl is smaller than that of the reactants, so the difference is released as heat. Such a reaction is said to be exothermic. The reverse of this reaction would absorb the same quantity of heat from the surroundings and be endothermic. In comparing the internal energies and enthalpies of different substances as we have been doing here, it is important to compare equal numbers of moles, because energy is an extensive property of matter. However, heats of reaction are commonly expressed on a molar basis and treated as intensive properties.

Changes in enthalpy and internal energy

We can characterize any chemical reaction by the change in the internal energy or enthalpy:

\[ΔH = H_{final} – H_{initial} \label{3-1}\]

The significance of this can hardly be exaggerated because ΔH, being a state function, is entirely independent of how the system gets from the initial state to the final state. In other words, the value of ΔH or ΔU for a given change in state is independent of the pathway of the process.

Consider, for example, the oxidation of a lump of sugar to carbon dioxide and water:

\[\ce{C12H22O11 + 12 O2(g) → 12 CO2(g) + 11 H2O(l)}\]

This process can be carried out in many ways, for example by burning the sugar in air, or by eating the sugar and letting your body carry out the oxidation. Although the mechanisms of the transformation are completely different for these two pathways, the overall change in the enthalpy of the system (the atoms of carbon, hydrogen and oxygen that were originally in the sugar) will be identical, and can be calculated simply by looking up the standard enthalpies of the reactants and products and calculating the difference

\[ΔH = [12 \times H(\ce{CO2})] + [11 \times H(\ce{H2O})] – H(\ce{C12H22O11}) = –5606\, kJ\]

The same quantity of heat is released whether the sugar is burnt in the air or oxidized in a series of enzyme-catalyzed steps in your body.

Enthalpy increases with temperature

When the temperature of a substance is raised, it absorbs heat. The enthalpy of a system increases with the temperature by the amount \(ΔH = C_p ΔT\). The defining relation

\[ΔH = ΔU + P ΔV\]

tells us that this change is dominated by the internal energy, subject to a slight correction for the work associated with volume change. Heating a substance causes it to expand, making ΔV positive and causing the enthalpy to increase slightly more than the internal energy. Physically, what this means is that if the temperature is increased while holding the pressure constant, some extra energy must be expended to push back the external atmosphere while the system expands. The difference between the dependence of U and H on temperature is only really significant for gases, since the coefficients of thermal expansion of liquids and solids are very small.

Enthalpy of phase changes

A plot of the enthalpy of a system as a function of its temperature is called an enthalpy diagram. The slope of the line is given by C_p. The enthalpy diagram of a pure substance such as water shows that this plot is not uniform, but is interrupted by sharp breaks at which the value of C_p is apparently infinite, meaning that the substance can absorb or lose heat without undergoing any change in temperature at all. This, of course, is exactly what happens when a substance undergoes a phase change; you already know that the temperature the water boiling in a kettle can never exceed 100 until all the liquid has evaporated, at which point the temperature of the steam will rise as more heat flows into the system.

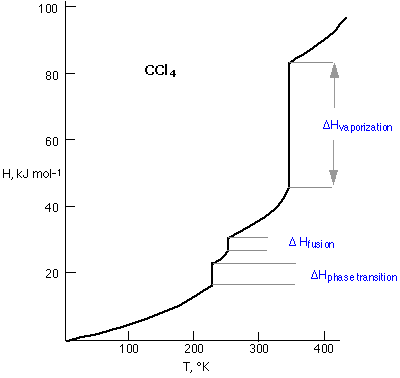
A plot of the enthalpy of carbon tetrachloride as a function of its temperature provides a concise view of its thermal behavior. The slope of the line is given by the heat capacity C_p. All H-vs.-C plots show sharp breaks at which the value of C_p is apparently infinite, meaning that the substance can absorb or lose heat without undergoing any change in temperature at all. This, of course, is exactly what happens when a substance undergoes a phase change; you already know that the temperature of the water boiling in a kettle can never exceed 100°C until all the liquid has evaporated, at which point the temperature (of the steam) will rise as more heat flows into the system.

The lowest-temperature discontinuity on the CCl₄ diagram corresponds to a solid-solid phase transition associated with a rearrangement of molecules in the crystalline solid.