10.4: Acid-Base Reactions

Learning Objectives

It is especially important that you know the precise meanings of all the highlighted terms in the context of this topic.

• Sketch out a proton-energy diagram for a strong acid, a weak acid or base, and for a strong base.
• Describe how the pH affects the relative concentrations of a conjugate acid-base pair.

Will this acid react with that base? And if so, to what extent? These questions can be answered quantitatively by carrying out the detailed equilibrium calculations you will learn about in another lesson. However, modern acid-base chemistry offers a few simple principles that can enable you to make a qualitative decision at a glance. More importantly, the ideas which we develop in this section are guaranteed to give you a far better conceptual understanding of proton-based acid-base reactions in general.

Which base gets the proton?

Will acid HA react with base B? We stated above that the outcome of any acid-base reaction depends on how well two different bases can compete in the tug-of-war for the proton

\[A^– \leftarrow H^+\rightarrow B^– \label{9.4.1}\]

The proton will always go to the stronger base. Some insight into this can be had by thinking of the proton as having different potential energies when it is bound to different acceptors. We can draw a useful analogy with the electrons in an atom, which, you will recall, will always fall into the lowest-potential energy orbitals available, filling them from the bottom up. In a similar way, protons will "fall" into the lowest-energy empty spots (bases) they can find.

Figure \(\PageIndex{1}\): A generalized proton soure-sink acid-base reaction.

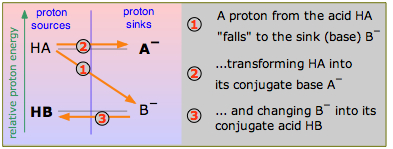
Consider the scheme shown here, which depicts two hypothetical acid-base conjugate pairs. Take careful note of the labeling of this diagram: the acids HA and HB are proton sources and the conjugate bases A^– and B^– are proton sinks. This "source-sink" terminology is synonymous with the "donor-acceptor" language that Brønsted taught us, but it also carries an implication about the relative energies of the proton as it exists in the two molecules HA and HB. If, as is indicated here, the proton is at a higher "potential energy" when it is in the form of HA than in HB, the reaction HA + B^– → HB + A ^– will be favored compared to the reverse process HB + A^– → HA + B^–, which would require elevating the proton up to the A^– level. In this example, HA is the stronger acid because its proton can fall to a lower potential energy when it joins with B^– to form HB.

We will refer to diagrams such as the one in Figure \(\PageIndex{1}\) as "proton-energy diagrams", which is not quite correct, but we do not want to get into thermodynamics at this point. (If you already know something about chemical thermodynamics, we are really referring to Gibbs energy.)

It follows, then, that if we can arrange all the common acid-base conjugate pairs on this kind of a scale, we can predict the direction of any simple acid-base reaction without resorting to numbers. This will be illustrated further on, but in order to keep things simple, let's look at a few proton-energy diagrams that illustrate some of the acid-base chemistry that we discussed in the preceding section.

Strong acids and weak acids

The hydronium ion is the dividing line; a strong acid, you will recall, is one whose conjugate base A^– loses out to the "stronger" base H₂O in the competition for the proton:

\[A^– \leftarrow H^+ \rightarrow H_2O \label{9.4.2}\]

An acid that is a stronger proton donor than hydronium ion is a "strong" acid; if it is a weaker proton donor than H₃O⁺, it is by definition "weak".This is seen most clearly in the diagram here, which contrasts the strong acid HA with the weak acid HB. HB "dissociates" to only a tiny extent because it is energetically unfavorable to promote its proton up to the H₂O-H₃O⁺ level (process 3 in the diagram).

Figure \(\PageIndex{2}\): proton-energy diagram for strong and weak acids

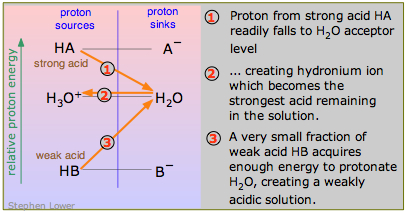
Strong acids and leveling

A strong acid, you will recall, is one whose conjugate base A^– loses out to the "stronger" base H₂O in the competition for the proton:

\[A^- ← H^+→ H_2O \label{9.4.3}\]

Because the reaction

\[HA + H_2O \rightarrow A^–+ H_3O^+ \label{9.4.4}\]

for any strong acid HA is virtually complete, all strong acids appear to be equally strong in water (the leveling effect.)

Figure \(\PageIndex{3}\): proton-energy diagram of leveling effect

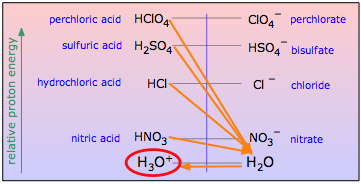
From the proton-energy standpoint, a strong acid is one in which the energy of the proton is substantially greater when attached to the anion A^–than when it is attached to H₂O. Adding a strong acid HA to water will put it in contact with a huge proton sink that drains off the protons from any such acid, leaving the conjugate base A^– along with hydronium ion, the strongest acid that can exist in water.

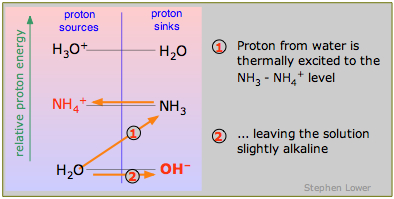
Weak bases

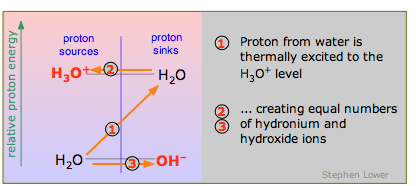
Conjugate bases of weak acids tend to accept protons from water, leaving a small excess of OH^– ions and thus an alkaline solution. As you can see in the diagram, the weak base ammonia accepts a proton from water:

\[NH_3 + H_2O \rightarrow NH_4^+ + OH^– \label{9.4.6}\]

The "weakness" of such a base is a consequence of the energetically unfavorable process (1) in which a proton must be raised up from the low-lying H₂O-OH^– level. From the standpoint of the "proton sources" column on the left, you can think of this as similar to the situation for weak acids that we discussed above; it can be considered a special case in which the weak acid is H₂O.

Figure \(\PageIndex{5}\): proton-energy diagram for weak base

The weakest acid and the strongest base

For a very long time, chemists had regarded methane, CH₄, as the weakest acid, making the methide ion CH₃^– (which is also the simplest carbanion) the strongest base. Methane still holds its position as the weakest acid, but in 2008, the ion LiO^–was found to be an even stronger base than CH₄^–. Because both of these bases are observable only in the gas phase, these facts have little obvious import on aqueous-solution chemistry.

Autoprotolysis

Because water is amphiprotic, one H₂O molecule can donate a proton to another, as explained above. In this case the proton has to acquire considerable energy to make the jump (1) from the H₂O-OH^– level to the H₃O⁺-H₂O level, so the reaction

\[2 H_2O \rightarrow H_3O^++ OH^– \label{9.4.7}\]

occurs only to a minute extent. Think of this as the special case of the "weakest" acid H₂O reacting with the "weakest" base H₂O.

Figure \(\PageIndex{6}\): proton-energy diagram of autoprotolysis

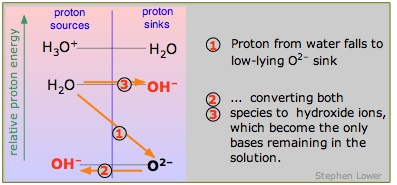
Strong bases

Finally, what is a strong base? Just as a strong acid lies above the H₃O⁺-H₂O level, so does a strong base lie below the H₂O-OH^– level. And for the same reason that H₃O⁺ is the strongest acid that can exist in water, OH^– is the strongest base that can exist in water. The example of the oxide ion O^2– is shown here. Sodium oxide Na₂O is a white powder that dissolves in water to give oxide ions which immediately decompose into hydroxide ions

\[O^{2–} + H_2O \rightarrow 2 OH^– \label{9.4.8}\]

Figure \(\PageIndex{7}\): proton-energy diagram of strong base

Putting it all together, and the meaning of pH

This table combines common examples covering the entire range of acid-base strengths, from the strong to the very weak. The energy scale at the left gives you some idea of the relative proton-energy levels for each conjugate pair; notice that the zero is arbitrarily set to that of the H₃O⁺-H₂O pair.

Figure \(\PageIndex{8}\): proton-free energy diagram for common acids and bases and pH

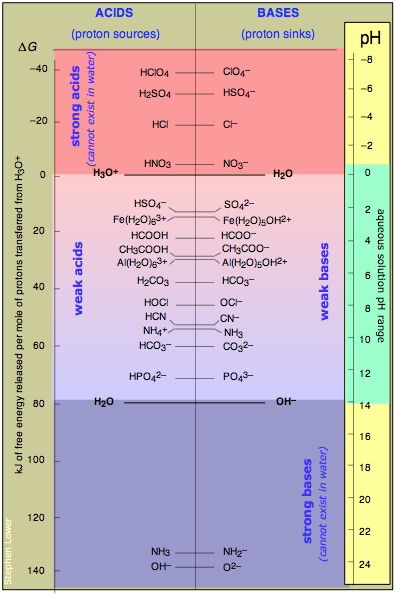
Of more importance is the pH scale on the right. The pH that corresponds to any conjugate pair is the pH at which equal concentrations of that pair are in their acid and base forms. For example, acetic acid CH₃COOH is "half ionized" at a pH of 4.7. If another strong acid such as HCl is added so as to reduce the pH, the proportion of acetate ion decreases, while if sodium hydroxide is added to force the pH higher, a larger fraction of the acetic acid will be "dissociated".

This illustrates another aspect of pH: at its most fundamental level, pH is an inverse measure of the "proton intensity" in the solution. The lower the pH, the higher the proton intensity, and the greater will be the fraction of higher-energy proton levels populated— which translates to higher acid-to-conjugate base concentration ratios. It is easy to see why acids such as H₂SO₄ and bases such as the amide ion NH₂^– cannot exist in aqueous solution; the pH would have to be at the impossible level of –6 for the former and +23 for the latter!

Why acids are titrated with hydroxide ion

When you titrate an acid with a base, you want virtually every molecule of the acid to react with the base. In the case of a weak acid such as hypochlorous, the reaction would be

\[HOCl + OH^– \rightarrow OCl^– + H_2O \label{9.4.9}\]

Because the proton level in HOCl is considerably above that in H₂O, titration with NaOH solution will ensure that every last proton is eaten up by the hydroxide ion. If, instead, you used ammonia NH₃ as a titrant, the closeness of the two proton levels would cause the reaction to be incomplete, yielding a less distinct equivalence point. And, of course, titration with a base that is weaker then hypochlorite ion (such as sodium bicarbonate) would be hopeless.

As a practical matter, you can usually estimate that when the pH differs by more than about two units from the value that corresponds to the conjugate-pair for a monoprotic acid, the concentration of the non-favored species will be down by a factor of around 1000.

Contributor

• Stephen Lower, Professor Emeritus (Simon Fraser U.) Chem1 Virtual Textbook