10.2: Aqueous Solutions- pH and Titrations
- Page ID
- 3486
Make sure you thoroughly understand the following essential ideas which have been presented above. It is especially important that you know the precise meanings of all the highlighted terms in the context of this topic.
- Define the ion product of water, and know its room-temperature value.
- State the criteria, in terms of H+ and OH– concentrations, of an acidic, alkaline, and a neutral solution.
- Given the effective hydrogen ion concentration in a solution, calculate the pH. Conversely, find the hydrogen- or hydroxide ion concentration in a solution having a given pH.
- Find the pH or pOH of a solution when either one is known.
- Describe the process of acid-base titration, and explain the significance of the equivalence point.
- Sketch a typical titration curve for a monoprotic or polyprotic acid.
As you will see in the lesson that follows this one, water plays an essential role in acid-base chemistry as we ordinarily know it. To even those who know very little about chemistry, the term pH is recognized as a measure of "acidity", so the major portion of this unit is devoted to the definition of pH and of the pH scale. But since these topics are intimately dependant on the properties of water and its ability do dissociate into hydrogen and hydroxyl ions, we begin our discussion with this topic. We end this lesson with a brief discussion of acid-base titration— probably the most frequently carried-out chemistry laboratory operation in the world.
Dissociation of water
The ability of acids to react with bases depends on the tendency of hydrogen ions to combine with hydroxide ions to form water:
H+(aq) + OH–(aq) → H2O (1)
This tendency happens to be very great, so the reaction is practically complete— but not "completely" complete; a few stray H+ and OH– ions will always be present. What's more, this is true even if you start with the purest water attainable. This means that in pure water, the reverse reaction, the "dissociation" of water
H2O → H+(aq) + OH–(aq) (2)
will proceed to a very slight extent. Both reactions take place simultaneously, but (1) is so much faster than (2) that only a minute fraction of H2O molecules are dissociated.
Liquids that contain ions are able to conduct an electric current. Pure water is practically an insulator, but careful experiments show that even the most highly purified water exhibits a very slight conductivity that corresponds to a concentration of both the H+ ion and OH– ions of almost exactly 1.00 × 10–7mol L–1 at 25°C.
All chemical reactions that take place in a single phase (such as in a solution) are theoretically "incomplete" and are said to be reversible.
What fraction of water molecules in a liter of water are dissociated
Solution: 1 L of water has a mass of 1000 g. The number of moles in 1000 g of H2O is
(1000 g)/(18 g mol–1) = 55.5 mol. This corresponds to (55.5 mol)(6.02E23 mol-1) = 3.34E25 H2O molecules.
An average of 10-7 mole, or (10-7)(6.02E23) = 6.0E16 H2O molecules will be dissociated at any time. The fraction of dissociated water molecules is therefore (6.0E16)/(3.3E25) = 1.8E–9.
Thus we can say that only about two out of every billion (109) water molecules will be dissociated.
Ion Product of water
The degree of dissociation of water is so small that you might wonder why it is even mentioned here. The reason stems from an important relationship that governs the concentrations of H+ and OH– ions in aqueous solutions:
[H+][OH–] = 1.00 × 10–14 (3)
must know this!
in which the square brackets [ ] refer to the concentrations (in moles per litre) of the substances they enclose.
Note
The quantity 1.00 x 10–14is commonly denoted by Kw. Its value varies slightly with temperature, pressure, and the presence of other ions in the solution.
This expression is known as the ion product of water, and it applies to all aqueous solutions, not just to pure water. The consequences of this are far-reaching, because it implies that if the concentration of H+ is large, that of OH– will be small, and vice versa. This means that H+ ions are present in all aqueous solutions, not just acidic ones.
This leads to the following important definitions, which you must know:
| acidic solution | [H+] > [OH–] |
| alkaline ("basic") solution | [H+] < [OH–] |
| neutral solution | [H+] = [OH–] = 1.00×10–7 mol L–1 |
Take special note of the following definition:
A neutral solution is one in which the concentrations of H+ and OH– ions are identical.The values of these concentrations are constrained by Eq. 3. Thus, in a neutral solution, both the hydrogen- and hydroxide ion concentrations are 1.00 × 10–7 mol L–1:
[H+][OH–] = [1.00 × 10–7][1.00 × 10–7] =1.00 × 10–14
Hydrochloric acid is a typical strong acid that is totally dissociated in solution:
HCl → H+(aq) + Cl–(aq)
A 1.0M solution of HCl in water therefore does not really contain any significant concentration of HCl molecules at all; it is a solution in of H+ and Cl– in which the concentrations of both ions are 1.0 mol L–1. The concentration of hydroxide ion in such a solution, according to Eq 2, is
[OH–] = (Kw)/[H+] = (1.00 x 10–14) / (1 mol L–1) = 1.00 x 10–14 mol L–1.
Similarly, the concentration of hydrogen ion in a solution made by dissolving 1.0 mol of sodium hydroxide in water will be 1.00 x 10–14 mol L–1.
2 pH
When dealing with a range of values (such as the variety of hydrogen ion concentrations encountered in chemistry) that spans many powers of ten, it is convenient to represent them on a more compressed logarithmic scale. By convention, we use the pH scale to denote hydrogen ion concentrations:
pH = – log10 [H+] (4) must know this!
or conversely, [H+] = 10–pH.
 This notation was devised by the Danish chemist Soren Sorenson (1868-1939) in 1909. There are several accounts of why he chose "pH"; a likely one is that the letters stand for the French term pouvoir hydrogène, meaning "power of hydrogen"— "power" in the sense of an exponent. It has since become common to represent other small quantities in "p-notation". Two that you need to know in this course are the following:
This notation was devised by the Danish chemist Soren Sorenson (1868-1939) in 1909. There are several accounts of why he chose "pH"; a likely one is that the letters stand for the French term pouvoir hydrogène, meaning "power of hydrogen"— "power" in the sense of an exponent. It has since become common to represent other small quantities in "p-notation". Two that you need to know in this course are the following:
pOH = – log10 [OH–]
pKw = – log Kw (= 14 when Kw = 1.00 × 10–14)
Note that pH and pOH are expressed as numbers without any units, since logarithms must be dimensionless.
Recall from Eq 3 that [H+][OH–] = 1.00 × 10–14; if we write this in "p-notation" it becomes
pH + pOH = 14
(5) must know this!
In a neutral solution at 25°C, pH = pOH = 7.0. As pH increases, pOH diminishes; a higher pH corresponds to an alkaline solution, a lower pH to an acidic solution. In a solution with [H+] = 1 M , the pH would be 0; in a 0.00010 M solution of H+, it would be 4.0. Similarly, a 0.00010 M solution of NaOH would have a pOH of 4.0, and thus a pH of 10.0. It is very important that you thoroughly understand the pH scale, and be able to convert between [H+] or [OH–] and pH in both directions.
The pH of blood must be held very close to 7.40. Find the hydroxide ion concentration that corresponds to this pH.
Solution: The pOH will be (14.0 – 7.40) = 6.60.
[OH–] = 10–pOH = 10–6.6 = 2.51 x 10–7 M
The pH scale
The range of possible pH values runs from about 0 to 14.
The word "about" in the above statement reflects the fact that at very high concentrations (10 M hydrochloric acid or sodium hydroxide, for example,) a significant fraction of the ions will be associated into neutral pairs such as H+·Cl–, thus reducing the concentration of “available” ions to a smaller value which we will call the effective concentration. It is the effective concentration of H+ and OH– that determines the pH and pOH. For solutions in which ion concentrations don't exceed 0.1 M, the formulas pH = –log [H+] and pOH = –log[OH–] are generally reliable, but don't expect a 10.0 M solution of a strong acid to have a pH of exactly –1.00!

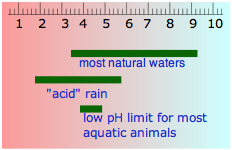
The table shown here will help give you a general feeling for where common substances fall on the pH scale. Notice especially that
- most foods are slightly acidic;
- the principal "bodily fluids" are slightly alkaline, as is seawater— not surprising, since early animal life began in the oceans.
- the pH of freshly-distilled water will drift downward as it takes up carbon dioxide from the air; CO2 reacts with water to produce carbonic acid, H2CO3.
- the pH of water that occurs in nature varies over a wide range. Groundwaters often pick up additional CO2 respired by organisms in the soil, but can also become alkaline if they are in contact with carbonate-containing sediments. "Acid" rain is by definition more acidic than pure water in equilibrium with atmospheric CO2, owing mainly to sulfuric and nitric acids that originate from fossil-fuel emissions of nitrogen oxides and SO2.
pH indicators
The colors of many dye-like compounds depend on the pH, and can serve as useful indicators to determine whether the pH of a solution is above or below a certain value.
Natural indicator dyes
|
|
 Many flower pigments are also dependent on the pH. You may have noticed that the flowers of some hydrangea shrub species are blue when grown in acidic soils, and white or pink in alkaline soils. Many flower pigments are also dependent on the pH. You may have noticed that the flowers of some hydrangea shrub species are blue when grown in acidic soils, and white or pink in alkaline soils. |
Red cabbage is a popular make-it-yourself indicator.
Universal indicators
Most indicator dyes show only one color change, and thus are only able to determine whether the pH of a solution is greater or less than the value that is characteristic of a particular indicator. By combining a variety of dyes whose color changes occur at different pHs, a "universal" indicator can be made. Commercially-prepared pH test papers of this kind are available for both wide and narrow pH ranges.

Titration
Since acids and bases readily react with each other, it is experimentally quite easy to find the amount of acid in a solution by determining how many moles of base are required to neutralize it. This operation is called titration, and you should already be familiar with it from your work in the Laboratory.
We can titrate an acid with a base, or a base with an acid. The substance whose concentration we are determining (the analyte) is the substance being titrated; the substance we are adding in measured amounts is the titrant. The idea is to add titrant until the titrant has reacted with all of the analyte; at this point, the number of moles of titrant added tells us the concentration of base (or acid) in the solution being titrated.
36.00 ml of a solution of HCl was titrated with 0.44 M KOH. The volume of KOH solution required to neutralize the acid solution was 27.00 ml. What was the concentration of the HCl?
Solution: The number of moles of titrant added was
(.027 L)(.44 mol L–1) = .0119 mol. Because one mole of KOH reacts with one mole of HCl, this is also the number of moles of HCl; its concentration is therefore
(.0119 mol) ÷ (.036 L) = 0.33 M .
Titration curves
The course of a titration can be followed by plotting the pH of the solution as a function of the quantity of titrant added. The figure shows two such curves, one for a strong acid (HCl) and the other for a weak acid, acetic acid, denoted by HAc. Looking first at the HCl curve, notice how the pH changes very slightly until the acid is almost neutralized. At that point, which corresponds to the vertical part of the plot, just one additional drop of NaOH solution will cause the pH to jump to a very high value— almost as high as that of the pure NaOH solution.
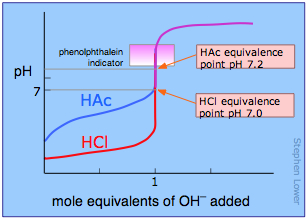
Compare the curve for HCl with that of HAc. For a weak acid, the pH jump near the neutralization point is less steep. Notice also that the pH of the solution at the neutralization point is greater than 7. These two characteristics of the titration curve for a weak acid are very important for you to know.
If the acid or base is polyprotic, there will be a jump in pH for each proton that is titrated. In the example shown here, a solution of carbonic acid H2CO3 is titrated with sodium hydroxide. The first equivalence point (at which the H2CO3 has been converted entirely into bicarbonate ion HCO3–) occurs at pH 8.3. The solution is now identical to one prepared by dissolving an identical amount of sodium bicarbonate in water.
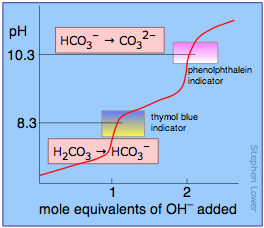
Addition of another mole equivalent of hydroxide ion converts the bicarbonate into carbonate ion and is complete at pH 10.3; an identical solution could be prepared by dissolving the appropriate amount of sodium carbonate in water.
Finding the equivalence point: indicators
When enough base has been added to react completely with the hydrogens of a monoprotic acid, the equivalence point has been reached. If a strong acid and strong base are titrated, the pH of the solution will be 7.0 at the equivalence point. However, if the acid is a weak one, the pH will be greater than 7; the “neutralized” solution will not be “neutral” in terms of pH. For a polyprotic acid, there will be an equivalence point for each titratable hydrogen in the acid. These typically occur at pH values that are 4-5 units apart, but they are occasionally closer, in which case they may not be readily apparent in the titration curve.
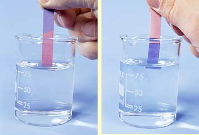
The key to a successful titration is knowing when the equivalence point has been reached. The easiest way of finding the equivalence point is to use an indicator dye; this is a substance whose color is sensitive to the pH. One such indicator that is commonly encountered in the laboratory is phenolphthalein; it is colorless in acidic solution, but turns intensely red when the solution becomes alkaline. If an acid is to be titrated, you add a few drops of phenolphthalein to the solution before beginning the titration. As the titrant is added, a local red color appears, but quickly dissipates as the solution is shaken or stirred. Gradually, as the equivalence point is approached, the color dissipates more slowly; the trick is to stop the addition of base after a single drop results in a permanently pink solution.
Different indicators change color at different pH values. Since the pH of the equivalence point varies with the strength of the acid being titrated, one tries to fit the indicator to the particular acid. One can titrate polyprotic acids by using a suitable combination of several indicators, as is illustrated above for carbonic acid.



 The best known of these is of course
The best known of these is of course