4.3: Formulas and Their Meaning
- Page ID
- 3605
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Make sure you thoroughly understand the following essential concepts that have been presented above.
- Explain why the symbol of an element often differs from the formula of the element..
- Define an ion, and explain the meaning of its formula.
- Find the simplest ("empirical") formula of a substance from a more complex molecular formula. Explain the meaning of the formula of an ionic solid such as NaCl.
- Define molecular weight, formula weight, and molar mass. Calculate any of these from any chemical formula.
- Given a chemical formula, express the mole ratios of any two elements, or the mole fraction of one of its elements.
- Find the percentage composition of a compound from its formula.
- Calculate the mass ratio of any two elements present in a compound from its formula.
- Find the empirical formula of a binary compound from the mole ratio of its two elements, expressed as a decimal number.
- Find the empirical formula of a binary compound from the mass ratio of its two elements.
- Find the empirical formula of a compound from its mass- or percentage composition.
At the heart of chemistry are substances — elements or compounds— which have adefinite composition which is expressed by a chemical formula. In this unit you will learn how to write and interpret chemical formulas both in terms of moles and masses, and to go in the reverse direction, in which we use experimental information about the composition of a compound to work out a formula.
The formula of a compound specifies the number of each kind of atom present in one molecular unit of a compound. Since every unique chemical substance has a definite composition, every such substance must be describable by a chemical formula.
The well-known alcohol ethanol is composed of molecules containing two atoms of carbon, five atoms of hydrogen, and one atom of oxygen. What is its molecular formula?
Solution
Just write the symbol of each element, following by a subscript indicating the number of atoms if more than one is present. Thus: C2H5O
Note that:
- The number of atoms of each element in a molecular formula is written as a subscript;
- When only a single atom of an element in a molecular formula is present, the subscript is omitted.
- In the case of organic (carbon-containing) compounds, it is customary to place the symbols of the elements C, H, (and if present,) O, N in this order in the formula.
Formulas of Elements and Ions
The symbol of an element is the one- or two-letter combination that represents the atom of a particular element, such as Au (gold) or O (oxygen). The symbol can be used as an abbreviation for an element name (it is easier to write "Mb" instead of "molybdenum"!) In more formal chemical use, an element symbol can also stand for one atom, or, depending on the context, for one mole of atoms of the element.
Some of the non-metallic elements exist in the form of molecules containing two or more atoms of the element. These molecules are described by formulas such as N2, S6, and P4. Some of these elements can form more than one kind of molecule; the best-known example of this is oxygen, which can exist as O2 (the common form that makes up 21% of the molecules in air), and also as O3, an unstable and highly reactive molecule known as ozone. The soccer-ball-shaped carbon molecules sometimes called buckyballs have the formula C60.
Allotropes
Different molecular forms of the same element (such as \(\ce{O_2}\) and \(\ce{O_3})\) are called allotropes.
Ions are atoms or molecules that carry an electrical charge. These charges are represented as superscripts in the ionic formulas. Thus:
| \(\ce{Cl^{-}}\) | the chloride ion, with one negative charge per atom |
| \(\ce{S^{2-}}\) | the sulfide ion carries two negative charges |
| \(\ce{HCO3^{2–}}\) | the carbonate ion— a molecular ion |
| \(\ce{NH4^{+}}\) | the ammonium ion |
Note that the number of charges (in units of the electron charge) should always precede the positive or negative sign, but this number is omitted when the charge is ±1.
Formulas of Extended Solids
In solid CdCl2, the Cl and Cd atoms are organized into sheets that extend indefinitely. Each atom is surrounded by six atoms of the opposite kind, so one can arbitrarily select any Cl–Cd–Cl as the "molecular unit". One such CdCl2 unit is indicated by the two red-colored bonds in the diagram, but it does not constitute a discrete "molecule" of CdCl2.
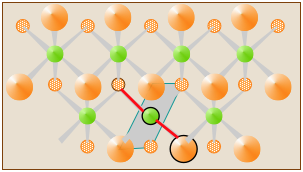
Many apparently "simple" solids exist only as ionic solids (such as NaCl) or as extended solids (such as CuCl2) in which no discrete molecules can be identified. The formulas we write for these compounds simply express relative numbers of the different kinds of atoms in the compound in the smallest possible integer numbers. These are identical with the empirical or "simplest" formulas that we discuss further on.
Many minerals and most rocks contain varying ratios of certain elements and can only be precisely characterized at the structural level. Because these are usually not pure substances, the "formulas" conventionally used to describe them have limited meanings. For example the common rock olivine, which can be considered a solid solution of Mg2SiO4 and Fe2SiO4, can be represented by (Mg,Fe)2SiO4. This implies that the ratio of the metals to SiO4 is constant, and that magnesium is usually present in greater amount than iron.
Empirical Formulas
Empirical formulas give the relative numbers of the different elements in a sample of a compound, expressed in the smallest possible integers. The term empirical refers to the fact that formulas of this kind are determined experimentally; such formulas are also commonly referred to as empirical formulas.
Glucose (the "fuel" your body runs on) is composed of molecular units having the formula C6H12O6. What is the empirical formula of glucose?
Solution
The glucose molecule contains twice as many atoms of hydrogen as carbons or oxygens, so we divide through by 6 to get CH2O.
Note: this empirical formula, which applies to all 6-carbon sugars, indicates that these compounds are "composed" of carbon and water, which explains why sugars are known as carbohydrates.
Some solid compounds do not exist as discrete molecular units, but are built up as extended two- or three-dimensional lattices of atoms or ions. The compositions of such compounds are commonly described by their empirical formulas. In the very common case of ionic solids, such a formula also expresses the minimum numbers of positive and negative ions required to produce an electrically neutral unit, as in NaCl or CuCl2.
- Write the formula of ferric bromide, given that the ferric (iron-III) ion is Fe3+ and the bromide ion carries a single negative charge.
- Write the formula of bismuth sulfide, formed when the ions Bi3+ and S2–combine.
Solution:
- Three Br– ions are required to balance the three positive charges of Fe3+, hence the formula FeBr3.
- The only way to get equal numbers of opposite charges is to have six of each, so the formula will be Bi2S3.
What formulas do not tell us
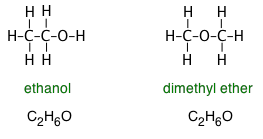
The formulas we ordinarily write convey no information about the compound's structure— that is, the order in which the atoms are connected by chemical bonds or are arranged in three-dimensional space. This limitation is especially significant in organic compounds, in which hundreds if not thousands of different molecules may share the same empirical formula. For example, both ethanol and dimethyl ether both have the empirical formula C2H6O, however the structural formulas reveal the very different nature of these two molecules:
More Complex Formulas
It is often useful to write formulas in such as way as to convey at least some information about the structure of a compound. For example, the formula of the solid (NH4)2CO3 is immediately identifiable as ammonium carbonate, and essentially a compound of ammonium and carbonate ions in a 2:1 ratio, whereas the simplest or empirical formula N2H8CO3 obscures this information.
Similarly, the distinction between ethanol and dimethyl ether can be made by writing the formulas as C2H5OH and CH3–O–CH3, respectively. Although neither of these formulas specifies the structures precisely, anyone who has studied organic chemistry can work them out, and will immediately recognize the –OH (hydroxyl) group which is the defining characteristic of the large class of organic compounds known as alcohols. The –O– atom linking two carbons is similarly the defining feature of ethers.
Several related terms are used to express the mass of one mole of a substance.
- Molecular weight :This is analogous to atomic weight: it is the relative weight of one formula unit of the compound, based on the carbon-12 scale. The molecular weight is found by adding atomic weights of all the atoms present in the formula unit. Molecular weights, like atomic weights, are dimensionless; i.e., they have no units.
- Formula weight :The same thing as molecular weight. This term is sometimes used in connection with ionic solids and other substances in which discrete molecules do not exist.
- Molar mass: The mass (in grams, kilograms, or any other unit) of one mole of particles or formula units. When expressed in grams, the molar mass is numerically the same as the molecular weight, but it must be accompanied by the mass unit.
- Calculate the formula weight of copper(II) chloride, \(\ce{CuCl2}\).
- How would you express this same quantity as a molar mass?
Solution
- The atomic weights of Cu and Cl are, respectively 63.55 and 35.45; the sum of each atomic weight, multiplied by the numbers of each kind of atom in the formula unit, yields: \[ 63.55 + 2(25.35) = 134.45.\]
- The masses of one mole of Cu and Cl atoms are, respectively, 63.55 g and 35.45 g; the mass of one mole of CuCl2 units is: \[(63.55 g) + 2(25.35 g) =134.45 g.\]
Interpreting formulas in terms of mole ratios and mole fractions
The information contained in formulas can be used to compare the compositions of related compounds as in the following example:
The ratio of hydrogen to carbon is often of interest in comparing different fuels. Calculate these ratios for methanol (CH3OH) and ethanol (C2H5OH).
Solution
The H:C ratios for the two alcohols are 4:1 = 4.0 for methanol and 6:2 (3.0) for ethanol.
Alternatively, one sometimes uses mole fractions to express the same thing. The mole fraction of an element M in a compound is just the number of atoms of M divided by the total number of atoms in the formula unit.
Calculate the mole fraction and mole-percent of carbon in ethanol (C2H5OH).
Solution
The formula unit contains nine atoms, two of which are carbon. The mole fraction of carbon in the compound is 2/9 = .22. Thus 22 percent of the atoms in ethanol are carbon.
Interpreting formulas in terms of masses of the elements
Since the formula of a compound expresses the ratio of the numbers of its constituent atoms, a formula also conveys information about the relative masses of the elements it contains. But in order to make this connection, we need to know the relative masses of the different elements.
Find the masses of carbon, hydrogen and oxygen in one mole of ethanol (C2H5OH).
Solution
Using the atomic weights (molar masses) of these three elements, we have
- carbon: (2 mol)(12.0 g mol–1) = 24 g of C
- hydrogen: (6 mol)(1.01 g mol–1) = 6 g of H
- oxygen: (1 mol)(16.0 g mol–1) = 16 g of O
The mass fraction of an element in a compound is just the ratio of the mass of that element to the mass of the entire formula unit. Mass fractions are always between 0 and 1, but are frequently expressed as percent.
Find the mass fraction and mass percentage of oxygen in ethanol (C2H5OH)
Solution
Using the information developed in the preceding example, the molar mass of ethanol is (24 + 6 + 16)g mol–1 = 46 g mol–1. Of this, 16 g is due to oxygen, so its mass fraction in the compound is (16 g)/(46 g) = 0.35 which corresponds to 35%.
Finding the percentage composition of a compound from its formula is a fundamental calculation that you must master; the technique is exactly as shown above. Finding a mass fraction is often the first step in solving related kinds of problems:
How many tons of potassium are contained in 10 tons of KCl?
Solution
The mass fraction of K in KCl is 39.1/74.6=.524; 10 tons of KCl contains(39.1/74.6) × 10 tons of K, or 5.24 tons of K. (Atomic weights: K = 39.1, Cl = 35.5. )
Note that there is no need to deal explicitly with moles, which would require converting tons to kg.
How many grams of KCl will contain 10 g of potassium?
Solution
The mass ratio of KCl/K is 74.6 ÷ 39.1; 10 g of potassium will be present in (74.6/39.1) × 10 grams of KCl, or 19 grams.
Mass ratios of two elements in a compound can be found directly from the mole ratios that are expressed in formulas.
Molten magnesium chloride (MgCl2) can be decomposed into its elements by passing an electric current through it. How many kg of chlorine will be released when 2.5 kg of magnesium is formed? (Mg = 24.3, Cl = 35.5)
Solution
The mass ratio of Cl/Mg is (35.5 ×2)/24.3, or 2.9; thus 2.9 kg of chlorine will be produced for every kg of Mg, or (2.9 × 2.5) = 7.2 kg of chlorine for 2.5 kg of Mg. (Note that is is not necessary to know the formula of elemental chlorine (Cl2) in order to solve this problem.)
Empirical formulas from Experimental data
As was explained above, the empirical formula (empirical formula) is one in which the relative numbers of the various elements are expressed in the smallest possible whole numbers. Aluminum chloride, for example, exists in the form of structural units having the composition Al2Cl6; the empirical formula of this substance is AlCl3. Some methods of analysis provide information about the relative numbers of the different kinds of atoms in a compound. The process of finding the formula of a compound from an analysis of its composition depends on your ability to recognize the decimal equivalents of common integer ratios such as 2:3, 3:2, 4:5, etc.
Analysis of an aluminum compound showed that 1.7 mol of Al is combined with 5.1 mol of chlorine. Write the empirical formula of this compound.
Solution
The formula Al1.7Cl5.1 expresses the relative numbers of moles of the two elements in the compound. It can be converted into the empirical formula by dividing both subscripts by the smaller one, yielding AlCl3 .
More commonly, an arbitrary mass of a compound is found to contain certain masses of its elements. These must be converted to moles in order to find the formula.
In a student lab experiment, it was found that 0.5684 g of magnesium burns in air to form 0.9426 g of magnesium oxide. Find the empirical formula of this compound. Atomic weights: Mg = 24.305, O=16.00.
Solution
Express this ratio as 0.375 g of C to 1.00 g of O.
- moles of carbon: (.375 g)/(12 g/mol) = 0.03125 mol C;
- moles of oxygen: (1.00 g)/(16 g/mol) = 0.0625 mol O
- mole ratio of C/O = 0.03125/0.0625 = 0.5;
this corresponds to the formula C0.5O, which we express in integers as CO2.
A 4.67-g sample of an aluminum compound was found to contain 0.945 g of Al and 3.72 g of Cl. Find the empirical formula of this compound. Atomic weights: Al = 27.0, Cl=35.45.
SolutionThe sample contains (0.945 g)/(27.0 g mol–1) = .035 mol of aluminum and (3.72 g)(35.45) = 0.105 mol of chlorine. The formula Al.035Cl.105 expresses the relative numbers of moles of the two elements in the compound. It can be converted into the empirical formula by dividing both subscripts by the smaller one, yielding AlCl3.
The composition of a binary (two-element) compound is sometimes expressed as a mass ratio. The easiest approach here is to treat the numbers that express the ratio as masses, thus turning the problem into the kind described immediately above.
A compound composed of only carbon and oxygen contains these two elements in a mass ratio C:H of 0.375. Find the empirical formula.
Solution
Express this ratio as 0.375 g of C to 1.00 g of O.
- moles of carbon: (.375 g)/(12 g/mol) = .03125 mol C;
- moles of oxygen: (1.00 g)/(16 g/mol) = .0625 mol O
- mole ratio of C/O = .03125/.0625 = 0.5;
this corresponds to the formula C0.5O, which we express in integers as CO2.
The composition-by-mass of a compound is most commonly expressed as weight percent (grams per 100 grams of compound). The first step is again to convert these to relative numbers of moles of each element in a fixed mass of the compound. Although this fixed mass is completely arbitrary (there is nothing special about 100 grams!), the ratios of the mole amounts of the various elements are not arbitrary: these ratios must be expressible as integers, since they represent ratios of integral numbers of atoms.
Find the empirical formula of a compound having the following mass-percent composition. Atomic weights are given in parentheses: 36.4 % Mn (54.9), 21.2 % S (32.06), 42.4 % O (16.0)
Solution100 g of this compound contains:
- Mn: (36.4 g) / (54.9 g mol–1) = 0.663 mol
- S: (21.2 g) / (32.06 g mol–1) = 0.660 mol
- O: (42.4 g) / (16.0 g mol–1) = 2.65 mol
The formula Mn .663S.660 O 2.65 expresses the relative numbers of moles of the three elements in the compound. It can be converted into the empirical formula by dividing all subscripts by the smallest one, yielding Mn 1.00S1.00 O 4.01which we write as MnSO4.
Note: because experimentally-determined masses are subject to small errors, it is usually necessary to neglect small deviations from integer values.
Find the empirical formula of a compound having the following mass-percent composition. Atomic weights are given in parentheses: 27.6 % Mn (54.9), 24.2 % S (32.06), 48.2 % O (16.0).
Solution
A preliminary formula based on 100 g of this compound can be written as
or
Mn.503S.754 O3.01
Dividing through by the smallest subscript yields Mn1S1.5O6 . Inspection of this formula suggests that multiplying each subscript by 2 yields the all-integer formula Mn2S3O12 .
Notes on experimental methods
One of the most fundamental operations in chemistry consists of breaking down a compound into its elements (a process known as analysis) and then determining the empirical formula from the relative amounts of each kind of atom present in the compound. In only a very few cases is it practical to carry out such a process directly: thus heating mercury(II) sulfide results in its direct decomposition:
\[\ce{2 HgS -> 2Hg + O2}.\]
Similarly, electrolysis of water produces the gases H2 and O2 in a 2:1 volume ratio.
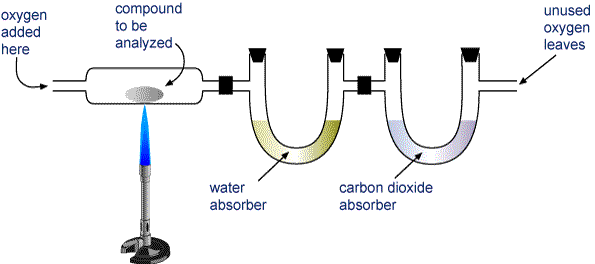
Most elemental analyses must be carried out indirectly, however. The most widely used of these methods has traditionally been the combustion analysis of organic compounds. An unknown hydrocarbon CaHbOc can be characterized by heating it in an oxygen stream so that it is completely decomposed into gaseous CO2 and H2O. These gases are passed through tubes containing substances which absorb each gas selectively. By careful weighing of each tube before and after the combustion process, the values of a and b for carbon and hydrogen, respectively, can be calculated. The subscript c for oxygen is found by subtracting the calculated masses of carbon and hydrogen from that of the original sample.
Since the 1970s, it has been possible to carry out combustion analyses with automated equipment. This one can also determine nitrogen and sulfur:
Measurements of mass or weight have long been the principal tool for understanding chemical change in a quantitative way. Balances and weighing scales have been in use for commercial and pharmaceutical purposes since the beginning of recorded history, but these devices lacked the 0.001-g precision required for quantitative chemistry and elemental analysis carried out on the laboratory scale.
It was not until the mid-18th century that the Scottish chemist Joseph Black invented the equal arm analytical balance. The key feature of this invention was a lightweight, rigid beam supported on a knife-edged fulcrum; additional knife-edges supported the weighing pans. The knife-edges greatly reduced the friction that limited the sensitivity of previous designs; it is no coincidence that accurate measurements of combining weights and atomic weights began at about this time.
Analytical balances are enclosed in a glass case to avoid interference from air currents, and the calibrated weights are handled with forceps to prevent adsorption of moisture or oils from bare fingers.
Anyone who was enrolled in college-level general chemistry up through the 1960's will recall the training (and tedium) associated with these devices. These could read directly to 1 milligram and allow estimates to ±0.1 mg. Later technical refinements added magnetic damping of beam swinging, pan brakes, and built-in weight sets operated by knobs. The very best research-grade balances achieved precisions of 0.001 mg.
Beginning in the 1970's, electronic balances have come into wide use, with single-pan types being especially popular. A single-pan balance eliminates the need for comparing the weight of the sample with that of calibrated weights. Addition of a sample to the pan causes a displacement of a load cellwhich generates a compensating electromagnetic field of sufficient magnitude to raise the pan to its original position. The current required to accomplish this is sensed and converted into a weight measurement. The best research-grade electronic balances can read to 1 microgram, but 0.1-mg sensitivities are more common for student laboratory use.


