19.7: Corrosion
- Page ID
- 349774
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To understand the process of corrosion.
CorrosionA galvanic process by which metals deteriorate through oxidation—usually but not always to their oxides. is a galvanic process by which metals deteriorate through oxidation—usually but not always to their oxides. For example, when exposed to air, iron rusts, silver tarnishes, and copper and brass acquire a bluish-green surface called a patina. Of the various metals subject to corrosion, iron is by far the most important commercially. An estimated $100 billion per year is spent in the United States alone to replace iron-containing objects destroyed by corrosion. Consequently, the development of methods for protecting metal surfaces from corrosion constitutes a very active area of industrial research. In this section, we describe some of the chemical and electrochemical processes responsible for corrosion. We also examine the chemical basis for some common methods for preventing corrosion and treating corroded metals.
Note the Pattern
Corrosion is a galvanic process.
Under ambient conditions, the oxidation of most metals is thermodynamically spontaneous, with the notable exception of gold and platinum. Hence it is actually somewhat surprising that any metals are useful at all in Earth’s moist, oxygen-rich atmosphere. Some metals, however, are resistant to corrosion for kinetic reasons. For example, aluminum in soft-drink cans and airplanes is protected by a thin coating of metal oxide that forms on the surface of the metal and acts as an impenetrable barrier that prevents further destruction. Aluminum cans also have a thin plastic layer to prevent reaction of the oxide with acid in the soft drink. Chromium, magnesium, and nickel also form protective oxide films. Stainless steels are remarkably resistant to corrosion because they usually contain a significant proportion of chromium, nickel, or both.
In contrast to these metals, when iron corrodes, it forms a red-brown hydrated metal oxide (Fe2O3·xH2O), commonly known as rust, that does not provide a tight protective film (Figure 19.17). Instead, the rust continually flakes off to expose a fresh metal surface vulnerable to reaction with oxygen and water. Because both oxygen and water are required for rust to form, an iron nail immersed in deoxygenated water will not rust—even over a period of several weeks. Similarly, a nail immersed in an organic solvent such as kerosene or mineral oil saturated with oxygen will not rust because of the absence of water.
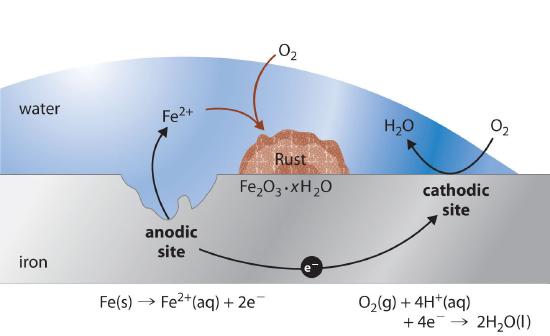
In the corrosion process, iron metal acts as the anode in a galvanic cell and is oxidized to Fe2+; oxygen is reduced to water at the cathode. The relevant reactions are as follows:
\(cathode:\; O_{2}\left ( g \right )+ 4H^{+}\left ( aq \right ) +4 e^{-} \rightarrow 2H_{2}O\left ( l \right ) \;\;\; E^{o}=1.23 \; V \tag{19.6.1} \)
\(anode:\; Fe\left ( s \right )\rightarrow Fe^{2+} \left ( aq \right ) +2e^{-} \;\;\; E^{o}=-0.24 \; V \tag{19.6.2} \)
\(overall:\; 2Fe\left ( s \right ) + O_{2}\left ( g \right )+ 4H^{+}\left ( aq \right ) \rightarrow 2Fe^{2+} \left ( aq \right ) + 2H_{2}O \left ( l \right ) \;\;\; E^{o}=1.68 \; V \tag{19.6.3} \)
The Fe2+ ions produced in the initial reaction are then oxidized by atmospheric oxygen to produce the insoluble hydrated oxide containing Fe3+, as represented in the following equation:
\( 4Fe^{2+} \left ( aq \right ) + O_{2}\left ( g \right ) + \left ( 2+4x \right )H_{2}O \left ( l \right )\rightarrow 2Fe_{2}O_{3}\cdot x H_{2}O +4H^{+} \tag{19.6.4} \)
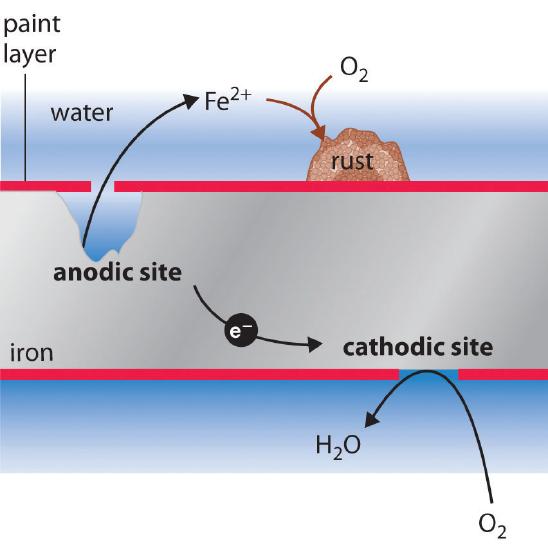
The sign and magnitude of E° for the corrosion process (Equation 19.6.3) indicate that there is a strong driving force for the oxidation of iron by O2 under standard conditions (1 M H+). Under neutral conditions, the driving force is somewhat less but still appreciable (E = 1.25 V at pH 7.0). Normally, the reaction of atmospheric CO2 with water to form H+ and HCO3− provides a low enough pH to enhance the reaction rate, as does acid rain. Automobile manufacturers spend a great deal of time and money developing paints that adhere tightly to the car’s metal surface to prevent oxygenated water, acid, and salt from coming into contact with the underlying metal. Unfortunately, even the best paint is subject to scratching or denting, and the electrochemical nature of the corrosion process means that two scratches relatively remote from each other can operate together as anode and cathode, leading to sudden mechanical failure (Figure 19.6.2).
One of the most common techniques used to prevent the corrosion of iron is applying a protective coating of another metal that is more difficult to oxidize. Faucets and some external parts of automobiles, for example, are often coated with a thin layer of chromium using an electrolytic process that will be discussed in Section 19.7. With the increased use of polymeric materials in cars, however, the use of chrome-plated steel has diminished in recent years. Similarly, the “tin cans” that hold soups and other foods are actually made of steel coated with a thin layer of tin. Neither chromium nor tin is intrinsically resistant to corrosion, but both form protective oxide coatings.
As with a protective paint, scratching a protective metal coating will allow corrosion to occur. In this case, however, the presence of the second metal can actually increase the rat that Fe is more easily oxidized than Sn. As a result, the more corrosion-resistant metal (in this case, tin) accelerates the corrosion of iron by acting as the cathode and providing a large surface area for the reduction of oxygen (Figure 19.6.3). This process is seen in some older homes where copper and iron pipes have been directly connected to each other. The less easily oxidized copper acts as the cathode, causing iron to dissolve rapidly near the connection and occasionally resulting in a catastrophic plumbing failure.

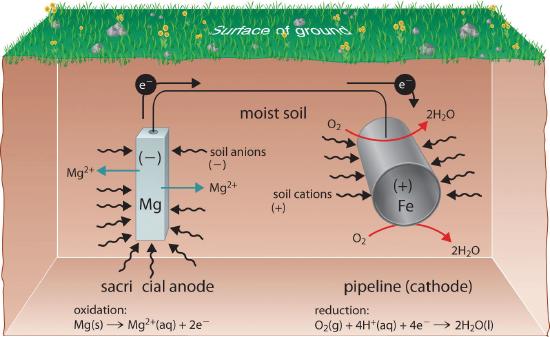
One way to avoid these problems is to use a more easily oxidized metal to protect iron from corrosion. In this approach, called cathodic protection, a more reactive metal such as Zn (E° = −0.76 V for Zn2+ + 2e− → Zn) becomes the anode, and iron becomes the cathode. This prevents oxidation of the iron and protects the iron object from corrosion. The reactions that occur under these conditions are as follows:
\(cathode:\; O_{2}\left ( g \right )+ 4H^{+}\left ( aq \right ) +4 e^{-} \rightarrow 2H_{2}O\left ( l \right ) \tag{19.6.5} \)
\(anode:\; Zn\left ( s \right )\rightarrow Zn^{2+} \left ( aq \right ) +2e^{-} \;\;\; E^{o}=-0.24 \; V \tag{19.6.6} \)
\(overall:\; 2Zn\left ( s \right ) + O_{2}\left ( g \right )+ 4H^{+}\left ( aq \right ) \rightarrow 2Zn^{2+} \left ( aq \right )+ 2H_{2}O \left ( l \right ) \ \tag{19.6.7} \)
The more reactive metal reacts with oxygen and will eventually dissolve, “sacrificing” itself to protect the iron object. Cathodic protection is the principle underlying galvanized steel, which is steel protected by a thin layer of zinc. Galvanized steel is used in objects ranging from nails to garbage cans. In a similar strategy, sacrificial electrodesAn electrode containing a more reactive metal that is attached to a metal object to inhibit that object’s corrosion. using magnesium, for example, are used to protect underground tanks or pipes (Figure 19.20). Replacing the sacrificial electrodes is more cost-effective than replacing the iron objects they are protecting.
Example 19.6.1
Suppose an old wooden sailboat, held together with iron screws, has a bronze propeller (recall that bronze is an alloy of copper containing about 7%–10% tin).
- If the boat is immersed in seawater, what corrosion reaction will occur? What is E°cell?
- How could you prevent this corrosion from occurring?
Given: identity of metals
Asked for: corrosion reaction, E°cell, and preventive measures
Strategy:
A Write the reactions that occur at the anode and the cathode. From these, write the overall cell reaction and calculate E°cell.
B Based on the relative redox activity of various substances, suggest possible preventive measures.
Solution:
- A According to Table 19.3.1, both copper and tin are less active metals than iron (i.e., they have higher positive values of E° than iron). Thus if tin or copper is brought into electrical contact by seawater with iron in the presence of oxygen, corrosion will occur. We therefore anticipate that the bronze propeller will act as the cathode at which O2 is reduced, and the iron screws will act as anodes at which iron dissolves:
\(cathode:\; O_{2}\left ( g \right )+ 4H^{+}\left ( aq \right ) +4 e^{-} \rightarrow 2H_{2}O\left ( l \right ) \;\;\; E_{cathode}^{o} = 1.23 \; V \)
\(anode:\; Fe\left ( s \right )\rightarrow Fe^{2+} \left ( aq \right ) + 2e^{-} \;\;\; E_{anode}^{o}=-0.45 \; V \)
\(overall:\; 2Fe\left ( s \right ) + O_{2}\left ( g \right )+ 4H^{+}\left ( aq \right ) \rightarrow 2Fe^{2+} \left ( aq \right )+ 2H_{2}O \left ( l \right ) \;\; E_{cell}^{o}=1.68 \; V\)
Over time, the iron screws will dissolve, and the boat will fall apart.
- B Possible ways to prevent corrosion, in order of decreasing cost and inconvenience, are as follows: disassembling the boat and rebuilding it with bronze screws; removing the boat from the water and storing it in a dry place; or attaching an inexpensive piece of zinc metal to the propeller shaft to act as a sacrificial electrode and replacing it once or twice a year. Because zinc is a more active metal than iron, it will act as the sacrificial anode in the electrochemical cell and dissolve (Equation 19.102).
Exercise
Suppose the water pipes leading into your house are made of lead, while the rest of the plumbing in your house is iron. To eliminate the possibility of lead poisoning, you call a plumber to replace the lead pipes. He quotes you a very low price if he can use up his existing supply of copper pipe to do the job.
- Do you accept his proposal?
- What else should you have the plumber do while at your home?
Answer
- Not unless you plan to sell the house very soon because the Cu/Fe pipe joints will lead to rapid corrosion.
- Any existing Pb/Fe joints should be examined carefully for corrosion of the iron pipes due to the Pb–Fe junction; the less active Pb will have served as the cathode for the reduction of O2, promoting oxidation of the more active Fe nearby.
Summary
The deterioration of metals through oxidation is a galvanic process called corrosion. Protective coatings consist of a second metal that is more difficult to oxidize than the metal being protected. Alternatively, a more easily oxidized metal can be applied to a metal surface, thus providing cathodic protection of the surface. A thin layer of zinc protects galvanized steel. Sacrificial electrodes can also be attached to an object to protect it.
Key Takeaway
- Corrosion is a galvanic process that can be prevented using cathodic protection.
Conceptual Problems
-
Do you expect a bent nail to corrode more or less rapidly than a straight nail? Why?
-
What does it mean when a metal is described as being coated with a sacrificial layer? Is this different from galvanic protection?
-
Why is it important for automobile manufacturers to apply paint to the metal surface of a car? Why is this process particularly important for vehicles in northern climates, where salt is used on icy roads?
Answer
-
Paint keeps oxygen and water from coming into direct contact with the metal, which prevents corrosion. Paint is more necessary because salt is an electrolyte that increases the conductivity of water and facilitates the flow of electric current between anodic and cathodic sites.


