21.7: Molecular Orbitals
- Page ID
- 49642
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\(\newcommand{\ket}[1]{\left| #1 \right>} \)
\( \newcommand{\bra}[1]{\left< #1 \right|} \)
\( \newcommand{\braket}[2]{\left< #1 \vphantom{#2} \right| \left. #2 \vphantom{#1} \right>} \)
\( \newcommand{\qmvec}[1]{\mathbf{\vec{#1}}} \)
\( \newcommand{\op}[1]{\hat{\mathbf{#1}}}\)
\( \newcommand{\expect}[1]{\langle #1 \rangle}\)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In order to explain both the ground state and the excited state involved in an absorption band in the ultraviolet and visible spectra of molecules, it is necessary to look at the electronic structure of molecules in somewhat different terms from the description given in the sections on Chemical Bonding and Further Aspects of Covalent Bonding. In those chapters we treated electrons either as bonding pairs located between two nuclei, or as lone pairs associated with a single nucleus. Such a model of electronic structure is known as the valence-bond model. It is of very little use in explaining molecular spectra because photons are absorbed by the whole molecule, not an individual atom or bond. Thus we need to look upon electrons in a molecule as occupying orbitals which belong to the molecule as a whole. Such orbitals are called molecular orbitals, and this way of looking at molecules is referred to as molecular-orbital (abbreviated MO) theory.
The term molecular orbital is mentioned in the discussion of The Covalent Bond when we described formation of a covalent bond in an H2 molecule as a result of overlap of two 1s atomic orbitals—one from each H atom. In that section, however, we do not point out that there are two ways in which the 1s electron wave of one H atom can combine with the 1s electron wave of another. One of these involves constructive interference between the two waves and is referred to as positive overlap. This results in a bigger electron wave (and hence more electron density) between the two atomic nuclei. This attracts the positively charged nuclei together, forming a bond as described in "The Covalent Bond". A molecular orbital formed as a result of positive overlap is called a bonding MO.
It is also possible to combine two electron waves so that destructive interference of the waves occurs between the atomic nuclei. This situation is referred to as negative overlap, and it decreases the probability of finding an electron between the nuclei. In the case of two H atoms this results in a planar node of zero electron density halfway between the nuclei. Without a buildup of negative charge between them, the nuclei repel each other and no chemical bond is possible. A molecular orbital formed as a result of negative overlap is called an antibonding MO.

If one or more electrons occupy an antibonding MO, the repulsion of the nuclei increases the energy of the molecule, and so such an orbital is higher in energy than a bonding MO. This is shown in Figure \(\PageIndex{1}\). Electron dot-density diagrams for the 1s electron in each of two separate H atoms are shown on the left and right sides of the figure. The horizontal lines show the energy each of these electrons would have. A dot-density diagram for a single electron occupying the bonding MO formed by positive overlap of the two orbitals is shown in the center of the diagram. This is labeled σ1s. Above it is a dot-density diagram for a single electron occupying the antibonding MO, σ1s*. (In general, antibonding MO’s are distinguished from bonding MO’s by adding an * to the label.) The energies of the molecular orbitals are indicated by the horizontal lines in the center of the diagram. The Greek letter σ in the labels for these orbitals refers to the fact that their positive or negative overlap occurs directly between the two atomic nuclei. Like an atomic orbital, each molecular orbital can accommodate two electrons. Thus the lowest energy arrangement for H2 would place both electrons in the a1s MO with paired spins. This molecular electron configuration is written (σ1s)2, and it corresponds to a covalent electron-pair bond holding the two H atoms together. If a sample of H2 is irradiated with ultraviolet light, however, an absorption band is observed between 110 and 170 nm. The energy of such an absorbed photon is enough to raise one electron to the antibonding MO, producing an excited state whose electron configuration is (σ1s)1(σ1s*)1. In this excited state the effects of the bonding and the antibonding orbitals exactly cancel each other; there is no overall bond between the two H atoms, and the H2 molecule dissociates. When the absorption of a photon results in the dissociation of a molecule like this, the phenomenon is called photodissociation. It occurs quite frequently when UV radiation strikes simple molecules.
The molecular-orbital model we have just described can also be used to explain why a molecule of He2 cannot form. If a molecule of He2 were able to exist, the four electrons would doubly occupy both the bonding and the antibonding orbitals, giving the electron configuration (σ1s)2(σ1s*)2. However, the antibonding electrons would cancel the effect of the bonding electrons, and there would be no resultant buildup of electronic charge between the nuclei and hence no bond. Interestingly enough, an extension of this argument predicts that if He2 loses an electron to become the He2+ ion, a bond is possible. He2+ would have the structure (σ1s)2(σ1s*)1 and the single electron in the antibonding orbital would only cancel half the effect of the two electrons in the bonding orbital. This would leave the ion with a “half-bond” joining the two nuclei. The spectrum of He shows bands corresponding to He2+, and from them it can be determined that He2+ has a bond enthalpy of 322 kJ mol–1.
The molecular-orbital model can easily be extended to other diatomic molecules in which both atoms are identical (homonuclear diatomic molecules). Three general rules are followed. First, only the core orbitals and the valence orbitals of the atoms need be considered. Second, only atomic orbitals whose energies are similar can combine to form molecular orbitals. Third, the number of molecular orbitals obtained is always the same as the number of atomic orbitals from which they were derived.
Applying these rules to diatomic molecules which consist of atoms from the second row of the periodic table, such as N2, O2, and F2, we need to consider the 1s, 2s, 2px, 2py, and 2pz atomic orbitals. Since the 1s orbital of each atom differs in energy from the 2s, we can overlap the two 1s orbitals separately from the 2s. This gives a σ1s and a σ1s* MO, as in the case of H2. Similarly, the 2s orbitals can be combined to give σ2s and σ2s* before we concern ourselves with the higher energy 2p orbitals. There are three 2p orbitals on each atom, and so we expect a total of six molecular orbitals to be derived from them.
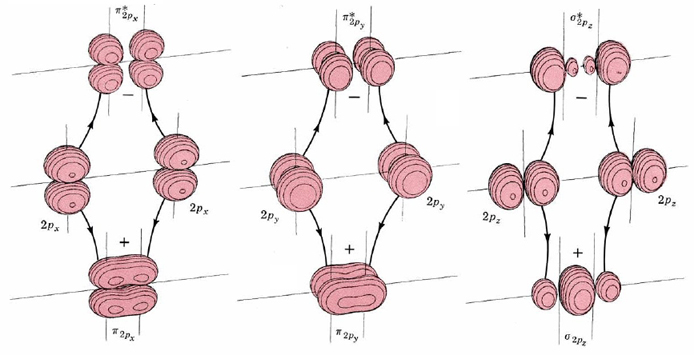
The shapes of these six molecular orbitals are shown by the boundary-surface diagrams in Figure \(\PageIndex{2}\). Two of them are formed by positive and negative overlap of 2px orbitals directly between the atomic nuclei. Consequently they are labeled σ2px and σ2px*. Two more molecular orbitals are formed by sideways overlap of 2px atomic orbitals. These are labeled π2px and π2px*, because the molecular orbitals have two parts—one above and one below a nodal plane containing the nuclei. The atomic 2py orbitals also overlap sideways to form π2py and π2py* molecular orbitals. These are identical to π2px and π2px*, except for a 90° rotation around the line connecting the nuclei. Consequently π2px and π2py have the same energy, as do π2px* and π2py*.
The electron configuration for any homonuclear diatomic molecule containing fewer than 20 electrons can be built up by filling electrons into the molecular orbitals we have just derived, starting with the orbital of lowest energy.

The relative energies of the molecular orbitals at the time they are being filled are shown in Figure \(\PageIndex{3}\). Like the energies of atomic orbitals given in Figure 1 from Electron Configurations, these relative molecular-orbital energies vary somewhat from one diatomic molecule to another. In particular the σ2p orbital is often lower than π2p. Nevertheless Figure \(\PageIndex{3}\) gives the correct order of filling the orbitals, and we can use it to determine molecular electron configurations.
Find the electronic configuration of the oxygen molecule, O2.
Solution
Starting with the lowest lying orbitals (σ1s and σ1s*) we add an appropriate number of electrons to successively higher orbitals in accord with the Pauli principle and Hund’s rule. O2 has 16 electrons, the first 14 of which are easily accommodated in the following way:
-
- \[ ( \sigma_{1s})^2 (\sigma_{1s}^* )^2 ( \sigma_{2s} )^2 (\sigma_{2s}^* )^2 ( \pi_{2p})^4 (\sigma_{2p})^2 \nonumber \]
The remaining two electrons must now be added to the π2px* orbitals. Since both these orbitals are of equal energy, one electron must be placed in each orbital and the spins must be parallel. The total electronic structure is thus
\[ (\sigma_{1s})^2 (\sigma_{1s}^*)^2 (\sigma_{2s})^2 (\sigma_{2s}^*)^2 ( \pi_{2p})^4 (\sigma_{2p})^2 (\pi_{2px}^*)^1 (\pi_{2py}^*)^1 \nonumber \]
As the previous problem shows, the molecular-orbital model predicts that O2 has two unpaired electrons. Substances whose atoms, molecules, or ions contain unpaired electrons are weakly attracted into a magnetic field, a property known as paramagnetism. (In a few special cases, such as iron, a much stronger magnetic attraction called ferromagnetism is also obsewed.) Most substances have all their electrons paired. Such materials are weakly repelled by a magnetic field, a property known as diamagnetism. Hence measurement of magnetic properties can tell us whether all electrons are paired or not. O2, for example, is found to be paramagnetic, an observation which agrees with the electron configuration predicted in Example 21.6. Before the advent of MO theory, however, the paramagnetism was a mystery, since the Lewis diagram predicted that all electrons should be paired.
The molecular-orbital model also allows us to estimate the strengths of bonds in diatomic molecules. We simply count each electron in a bonding orbital as contributing half a bond, while each electron in an antibonding orbital takes away half a bond. Thus if there are B electrons in bonding orbitals and A electrons in antibonding orbitals, the net bond order is given by
\[ \text{ Bond order} = \frac{A-B}{2} \nonumber \]
The larger the bond order, the more strongly the atoms are held together.
Calculate the bond order for the molecule N2.
Solution
There are 14 electrons, and so the electron configuration is
\[ ( \sigma_{1s})^2 (\sigma_{1s}^* )^2 ( \sigma_{2s} )^2 (\sigma_{2s}^* )^2 ( \pi_{2p})^4 (\sigma_{2p})^2 \nonumber \]
There are a total of 2 + 2 + 4 + 2 = 10 electrons in bonding MO’s and only 4 in the antibonding orbitals σ1s* and σ2s*. Thus
\[ \text{ Bond order} = \frac{10-4}{2} = 3 \nonumber \]
The bond orders derived from the molecular-orbital model for stable molecules agree exactly with those predicted by Lewis’ theory. Not only do we find a triple bond for N2, but we also find a double bond for O2 and a single bond for F2. The results of such bond-order calculations are summarized in Table 1.
| Molecule* | Bond Order | Bond Enthalpy/kJ mol–1 | Bond Length/pm |
|---|---|---|---|
| $$\text{H}^{+}_{2}$$ | $$\frac{1}{2}$$ | $$256$$ |
$$106$$
|
| $$\text{H}_2$$ | $$432$$ |
$$74$$
|
|
| $$\text{He}^{+}_{2}$$ | $$\frac{1}{2}$$ | $$322$$ |
$$108$$
|
| $$\text{He}_2$$ |
|
|
|
| $$\text{Li}_2$$ |
|
$$110$$ |
$$267$$
|
| $$\text{Be}_2$$ |
|
|
|
| $$\text{B}_2$$ |
|
$$274$$ |
$$159$$
|
| $$\text{C}_2$$ |
|
$$603$$ |
$$124$$
|
| $$\text{N}_2$$ |
|
$$942$$ |
$$110$$
|
| $$\text{O}_2$$ |
|
$$494$$ |
$$121$$
|
| $$\text{F}_2$$ |
|
$$139$$ |
$$142$$
|
| $$\text{Ne}_2$$ |
|
|
|
* Some molecule-ions such as H2+ are included. Except fur the number of electrons involved, the MO theory is applied to them in exactly the same way as to molecules.
Some of the molecules in the table, such as C2 and B2, are only stable at high temperatures or only exist transitorily in discharge tubes, and so you are probably not familiar with them. Nevertheless, their spectra can be studied. Also included in the table are values for the bond enthalpies and bond lengths of the various species obtained from their spectra. Note the excellent qualitative agreement with the MO theory. The higher the bond order predicted by the theory, the larger the bond enthalpy and the shorter the bond length.


