21.8: Delocalized Electrons
- Page ID
- 49643
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)One of the most useful aspects of molecular-orbital theory only becomes apparent when we consider molecules containing three or more atoms. According to molecular-orbital theory, electrons occupy orbitals which are delocalized. That is, the orbitals spread over the entire molecule. An electron is not confined only to the vicinity of one or two atomic nuclei as in the lone pairs and bond pairs of valence-bond theory. As seen in the section on Resonance, there are some molecules, such as O3 and C6H6, which cannot be described adequately by a single Lewis diagram. In such cases valence-bond theory resorts to resonance hybrids, such as

for ozone. The same molecules can be handled by MO theory without the need for several contributing structures, because electrons can occupy orbitals belonging to the molecule as a whole.
As an example of this we shall apply MO theory to the pi orbitals in ozone. The sigma bonds in this molecule may be attributed to overlap of sp2 hybrid orbitals on each of the three oxygen atoms. You will recall that sp2 hybrids are directed toward the corners of an equilateral triangle, in reasonable agreement with the 117° angle in ozone. For the sigma bonds and lone pairs, then, we have the Lewis diagram
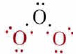
This involves only 14 of the 18 valence electrons of the three oxygens, and so 4 electrons are left for pi bonding. Furthermore, each oxygen has a p orbital perpendicular to the plane of its sp2 hybrids (that is, perpendicular to the plane of the three oxygen atoms), which has not yet been used for bonding.
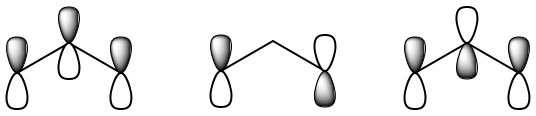
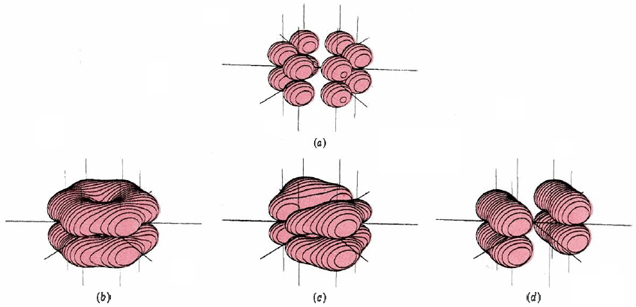
These three remaining p orbitals can overlap sideways to form molecular orbitals, which are included in the jmol shown here. Using the scroll bar, you may select which molecular orbital to display for the ozone molecule. In order to demonstrate delocalized electrons, we will focus on three of the molecular orbitals shown. The first of these orbitals to highlight is seen by selecting the orbital labeled "N7" in the scroll menu. This orbital shows a concentrated electron density between the central oxygen and each of the other two, and is therefore a bonding MO. The second to focus on is orbital "N10", which looks very similar to the original atomic p orbitals on the end oxygen atoms. An electron in this orbital neither strengthens nor weakens the attractions between the atoms, and so the MO is said to be nonbonding. Finally, there is an antibonding MO which has nodes between each pair of oxygen atoms and can be seen by selecting orbital "N13". Since there are only four electrons, only the two lower-energy MO’s (the bonding and nonbonding) will be occupied. The two electrons in the bonding MO provide a bond order of 1, but this is spread over both O—O bonds, and so it contributes a bond order of one-half between each pair of oxygens. Similarly the two electrons in the nonbonding MO correspond to a lone pair, half on the left oxygen and half on the right. Including the sigma bonding framework, this gives 1½ bonds between each pair of oxygens and 2½ lone pairs on each end oxygen. This is exactly the average of the two resonance structures already given.
The MO treatment can also be used to interpret the spectrum of ozone. Ozone in the earth’s stratosphere absorbs much solar ultraviolet radiation which would otherwise cause damage to the biosphere. This absorption is due to a band centered around 255 nm which corresponds to excitation of an electron to the unfilled antibonding pi orbital shown in Figure \(\PageIndex{1}\) c.
Another important molecule to which MO theory can be applied usefully is benzene. As described in "Resonance," benzene can be represented by the resonance hybrid
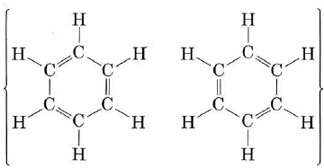
This indicates that all C—C bonds are equivalent and intermediate between a single and a double bond. As in the case of ozone, we can treat the sigma bonds of benzene in valence-bond terms, dealing only with pi bonding by the molecular-orbital, method. The sigma bonding framework is
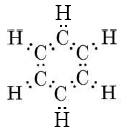
This involves 24 electrons in bonds formed by overlap of sp2 hybrid orbitals on the carbon atoms with 1s orbitals on each hydrogen or with other sp2 hybrids on other carbons. This gives a planar framework and leaves six p orbitals (one on each carbon) which are perpendicular to the molecular plane and can overlap sideways to form six pi molecular orbitals. Only the three lowest-energy MO’s are occupied, and their electron clouds are shown in Figure \(\PageIndex{2}\). All these MO’s are bonding, while the three not shown are anti- bonding. When the six valence electrons not used for sigma bonding occupy the pi-bonding MO’s, they are evenly distributed around the ring of carbon atoms. This contributes a bond order of one-half between each pair of carbons, or a total bond order of 1½ when the sigma bond is included. Thus the C—C bond is intermediate between a single and double bond, in accord with the resonance hybrid.