21.9: Conjugated Systems
- Page ID
- 49644
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In some molecules the delocalization of electron pairs can be very much more extensive than in ozone and benzene. This is particularly true of carbon compounds containing conjugated chains, i.e., long chains of alternating single and double bonds. An example is provided by vitamin A2 which has the structure
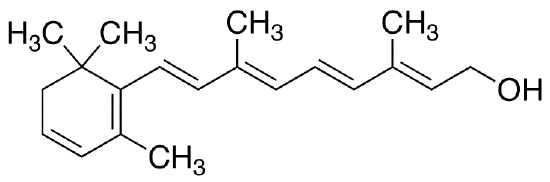
Both the physical and chemical properties of this molecule indicate that all the bonds in the conjugated chain (shown in color) are intermediate in character between single and double bonds and that the pi electrons are free to move over the whole length of the conjugated chain.
A very simple, though approximate, method of handling delocalized electrons mathematically is to treat them as though they were particles in a one-dimensional box of the same length as the chain. In the case of vitamin A2 the distance from the carbon atom at one end of the conjugated chain to that on the other is about 1210 pm. If we feed this value and the mass of the electron (9.110 × 10–31 kg) into the particle-in-the-box formula (Equation \(\ref{1}\)), we can obtain approximate values of the energy levels occupied by the delocalized electrons:
\[E_{k}=\dfrac{1}{2m}\left(\dfrac{nh}{2d}\right)^{2}=\dfrac{1}{2\times9.110\times10^{-31} \text{ kg}}\left(\dfrac{n\times6.626\times10^{-34} \text{J s }}{2\times 1210\times 10^{-12} \text{ m}}\right) ^{2} \label{1} \]
\[E_{k}=n^{2}(4.11\times10^{-20} \text{ J}) \label{2} \]
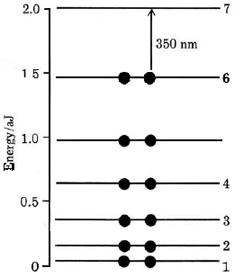
The first seven energy levels derived from this formula are shown in Figure \(\PageIndex{2}\). Note that since there are 12 pi electrons (one for each carbon atom on the conjugate chain), these will occupy the six lowest levels in accord with the Pauli principle.
This model allows us to calculate the wavelength of the main absorption band in the spectrum of vitamin A2. If an electron from the highest occupied level (n = 6) is excited to the lowest unoccupied level (n = 7), the energy required can be calculated from Equation \(\ref{2}\):
\[\Delta E = E_{7}-E_{6}=(7^{2}-6^{2})\times4.11\times10^{-20} \text{ J}=5.34\times10^{-19} \text{ J} \nonumber \]
Thus
\[ λ = \dfrac{hc}{\Delta E} = \dfrac{6.626\times10^{-34} \text{ Js}\times2.998\times0^{8} \text{ ms}^{-1}}{5.34\times10^{-19} \text{ J}} = 327 \text{ nm} \nonumber \]
This is in reasonable agreement with the observed value of 350 nm, considering the approximate nature of the model.
As a general rule, the longer a conjugated chain, the longer the wavelength at which it absorbs. Ethene (C2H4), for example, has only one double bond and absorbs at 170 nm. Hexatriene (C6H8) has three alternating double bonds and absorbs at 265 nm, while vitamin A2, with six double bonds, absorbs at 350 nm. It is not difficult to explain this effect in terms of the particle-in-a-box model. According to Equation \(\ref{1}\) the energy of a level varies inversely with the square of the length of the box. Thus the longer the conjugated chain, the closer the energy levels will be to each other, and the less energy a photon need have to excite an electron. Naturally the lower the energy of a photon, the longer its wavelength will be.
A similar effect is found for molecules containing several benzene rings. Since these correspond to Lewis formulas of alternating double and single bonds, they can also be regarded as conjugated systems containing delocalized electrons. Experimentally we find that the more benzene rings a molecule contains, the longer the wavelengths at which it absorbs:

Thus increasing the extent of electron delocalization increases the wavelength at which a molecule will absorb light, whether the electron is delocalized over rings or chains.
This behavior of delocalized electrons is important in the preparation of compounds which strongly absorb visible light, i.e., in the preparation of dyes. Very few compounds which are held together by sigma bonds alone are colored. The electrons are so tightly held that a very energetic photon is needed to excite them. In order for an organic molecule to absorb in the visible region of the spectrum, it must usually contain very delocalized pi electrons. Thus most dyes and most colored compounds occurring in living organisms turn out to be large molecules with extensive systems of conjugated double bonds.


