7.14: Resonance
- Page ID
- 49400
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In addition to molecules containing odd numbers of electrons, there is another class of molecules which does not fit easily into the electron-pair theory of the covalent bond. For these molecules it is possible to draw more than one Lewis structure which obeys the octet rule but which is unsatisfactory in other ways. A simple example of such a molecule is ozone, an unusual form of oxygen, whose molecular formula is O3. Like the oxides of nitrogen, ozone is important in a discussion of atmospheric-pollution problems, but for the moment we will confine ourselves to its structure.
We can draw two Lewis diagrams for O3, both of which obey the octet rule:
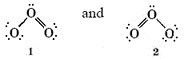
Structure 1 suggests that there is an O―O single bond on the left and an  double bond on the right side of the molecule. Structure 2 suggests the opposite placement of the double bond. However, it seems unlikely that electrons should be able to distinguish left from right in this way, and experimental evidence confirms this suspicion. Both bonds are found to have the same length, namely, 128 pm. This is intermediate between the
double bond on the right side of the molecule. Structure 2 suggests the opposite placement of the double bond. However, it seems unlikely that electrons should be able to distinguish left from right in this way, and experimental evidence confirms this suspicion. Both bonds are found to have the same length, namely, 128 pm. This is intermediate between the  double-bond length of 121 pm in O2 and the O―O single-bond length of 147 pm in H2O2. In other words the structure of O2 is somehow intermediate in character between the two structures shown.
double-bond length of 121 pm in O2 and the O―O single-bond length of 147 pm in H2O2. In other words the structure of O2 is somehow intermediate in character between the two structures shown.
On a mathematical level, we can satisfactorily account for the properties of ozone by regarding its structure as a hybrid of the two structures shown above, the term hybrid having exactly the same sense as for hybrids. We then obtain an electron probability distribution in which both bonds receive equal treatment and are intermediate in character between double and single bonds. Such a structure is called a resonance hybrid and is indicated in one of the following ways:
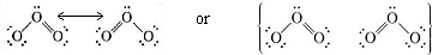
The term resonance and the use of a double-headed arrow,  , are both unfortunate since they suggest that the structure is continually oscillating between the two alternatives, so that if only you were fast enough, you could “catch” the double bond on one side or the other. One can no more do this than “catch” an sp hybrid orbital instantaneously in the form of an s or a p orbital.
, are both unfortunate since they suggest that the structure is continually oscillating between the two alternatives, so that if only you were fast enough, you could “catch” the double bond on one side or the other. One can no more do this than “catch” an sp hybrid orbital instantaneously in the form of an s or a p orbital.
The most important example of resonance is undoubtedly the compound benzene, C6H6, which has the structure
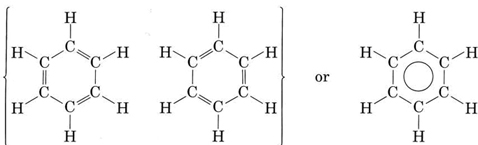
The circle within the second formula indicates that all C—C bonds in the hexagon are equivalent. This hexagonal ring of six carbon atoms is called a benzene ring. Each carbon-carbon bond is 139 pm long, intermediate between the length of a C―C single bond (154 pm) and a 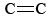 double bond (135 pm). Whereas a double bond between two carbon atoms is normally quite reactive, the bonding between the carbons in the benzene ring is difficult to alter. In virtually all its chemical reactions, the ring structure of benzene remains intact.
double bond (135 pm). Whereas a double bond between two carbon atoms is normally quite reactive, the bonding between the carbons in the benzene ring is difficult to alter. In virtually all its chemical reactions, the ring structure of benzene remains intact.
Even when a molecule exhibits resonance, it is still possible to predict its shape. Any bonds which are intermediate in character can be treated as though they were single bonds, though perhaps a bit fatter. On this basis one would predict that the ozone molecule is angular rather than linear because of the lone pair on the central oxygen atom, with an angle slightly less than 120°. Experimentally the angle is 117°. In the same way each carbon atom in benzene can be expected to be surrounded by three atoms in a plane around it, separated by angles of approximately 120°. Again this agrees with experiment. All the atoms in C6H6 lie in the same plane, and all bond angles are 120°.
Write resonance structures to indicate the bonding in the carbonate ion, CO32–. Predict the O—C—O angle and the carbon-oxygen bond length.
Solution
We must first write a plausible Lewis structure for the ion. Counting valence electrons, we have a total of
4(from C) + 3 × 6(from O) + 2(from charge) = 24 electrons
There are 4 octets to be filled, making a total of 4 × 8 = 32 electrons. We must thus count 32 – 24 = 8 electrons twice, and so there are 4 shared pairs. Since there are only three oxygen atoms, one must be double bonded to the carbon atom:
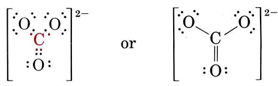
Two other equivalent structures can also be drawn, and so the carbonate ion corresponds to the following resonance hybrid:
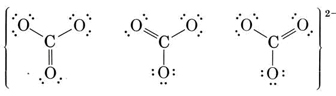
Since the carbon has no lone pairs in its valence shell, the three oxygens should be arranged trigonally around the carbon and all four atoms should lie in a plane. As we saw in the previous chapter, the C—O single-bond length is 143 pm, while the 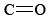 double-bond length is 122 pm. We can expect the carbon-oxygen distance in the carbonate ion to lie somewhere in between these values. Experimentally it is found to be 129 pm.
double-bond length is 122 pm. We can expect the carbon-oxygen distance in the carbonate ion to lie somewhere in between these values. Experimentally it is found to be 129 pm.


