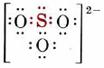7.13: Formal Charge and Oxidation Numbers
- Page ID
- 49398
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Formal Charge
On the page discussing the covalent bond, it is shown that the density of electrons in a covalent bond is shared between both atoms. When drawing Lewis Structures it is sometimes useful to see which structure can be deemed the best. The Formal Charge is a somewhat artificial device that exists in the minds of chemists (not within the molecules, themselves) to help keep track of electrons in their bonding configurations. The Formal Charge is the charge an atom in a molecule or polyatomic ion would have if all of the bonding electrons were divided equally between atoms in the bond.
Here are some rules for determining the Formal Charge on each atom in a molecule or polyatomic ion:
- Electrons within a Lone Pair on an atom are assigned exclusively to that atom.
- Half of the electrons in each bond around an atom are assigned to that atom.
- The Formal Charges on all atoms in a molecule must sum to zero; for a polyatomic ion the Formal Charges must sum to the charge on the ion (which may be positive or negative).
The Formal Charge is defined by the relationship:
Formal Charge = [number of valence electrons in an isolated atom] - [(number of lone pair electrons) + ½ (number of bonding electrons)]
With the definitions above, we can calculate the Formal Charge on the thiocyanate Ion, SCN-:
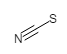 |
S | C | N |
|---|---|---|---|
| Valence electrons | 6 | 4 | 5 |
| Lone pair electrons | 6 | 0 | 2 |
| Shared electrons (bonds) | 2 (1) | 8 (4) | 6 (3) |
| Formal Charge = | 6 - (6 + ½·2) | 4 - (0 + ½·8) | 5 - (2 + ½·6) |
| Formal Charge | -1 | 0 | 0 |
Notice how the sum of all of the formal charges adds up to the charge of the thiocyanate ion (-1). When drawing Lewis Structures, we use this information to determine which structure would be the most likely. The following rules apply:
- Smaller absolute Formal Charges are more favorable (recall that the absolute value of a number is > 0)
- Negative Formal Charges should be on the most electronegative atoms
- Like charges should not be on adjacent atoms
Oxidation Numbers
We have also discussed electronegativity, which gives rise to polarity in bonds and molecules. Thus, sometimes it is helpful for us to define another somewhat artificial device - invented by chemists, not by molecules - which enables us to keep track of electrons in complicated reactions where electrons rearrange into new bonds.
We can obtain oxidation numbers by arbitrarily assigning the electrons of each covalent bond to the more electronegative atom in the bond. This is in contrast to the Formal Charge which divides each bonding pair equally without concern for which atom may be more electronegative. When this division has been done for all bonds, the charge remaining on each atom is said to be its oxidation number. If two like atoms are joined, each atom is assigned half the bonding electrons.
Determine the oxidation number of each atom in each of the following formulas: (a) Cl2; (b) CH4; (c) NaCl; (d) OF2; (e) H2O2.
Solution:
In each case we begin by drawing a Lewis diagram:

In each Lewis diagram, electrons have been color coded to indicate the atom from which they came originally. The boxes enclose electrons assigned to a given atom by the rules for determining oxidation number.
a) Since the bond in Cl2 is purely covalent and the electrons are shared equally, one electron from the bond is assigned to each Cl, giving the same number of valence electrons (7) as a neutral Cl atom. Thus neither atom has lost any electrons, and the oxidation number is 0. This is indicated by writing a 0 above the symbol for chlorine in the formula
\[\overset{0}{\mathop{\text{Cl}}}\,_{\text{2}} \nonumber \]
b) Since C is more electronegative than H, the pair of electrons in each C―H bond is assigned to C. Therefore each H has lost the one valence electron it originally had, giving an oxidation number of +1. The C atom has gained four electrons, giving it a negative charge and hence an oxidation number of – 4:
\[\overset{-\text{4}}{\mathop{\text{C}}}\,\overset{\text{+1}}{\mathop{\text{H}}}\,_{\text{4}} \nonumber \]
c) In NaCl each Na atom has lost an electron to form an Na+ ion, and each Cl atom has gained an electron to form Cl–. The oxidation numbers therefore correspond to the ionic charges:
\[\overset{\text{+1}}{\mathop{\text{Na}}}\,\overset{-\text{1}}{\mathop{\text{Cl}}}\, \nonumber \]
d) Since F is more electronegative than O, the bonding pairs are assigned to F in oxygen difluoride (OF2). The O is left with four valence electrons, and each F has eight. The oxidation numbers are
\[\overset{\text{+2}}{\mathop{\text{O}}}\,\overset{-\text{1}}{\mathop{\text{F}_{\text{2}}}}\, \nonumber \]
e) In Hydrogen peroxide (H2O2) the O—H bond pairs are assigned to the more electronegative O’s, but the O―O bond is purely covalent, and the electron pair is divided equally. This gives each O seven electrons, a gain of 1 over the neutral atom. The oxidation numbers are
\[\overset{\text{+1}}{\mathop{\text{H}_{\text{2}}}}\,\overset{-\text{1}}{\mathop{\text{O}_{\text{2}}}}\, \nonumber \]
Although one could always work out Lewis diagrams to obtain oxidation numbers as shown in Example \(\PageIndex{1}\), it is often easier to use a few simple rules to obtain them. The rules summarize the properties of oxidation numbers illustrated in Example \(\PageIndex{2}\).
- The oxidation number of an atom in an uncombined element is 0. Since atoms of the same element always form pure covalent bonds, they share electrons equally, neither losing nor gaining, e.g., Cl2.
- The oxidation number of a monatomic ion equals the charge on that ion, e.g., Na+ and Cl–.
- Some elements have the same oxidation number in nearly all their compounds.
- Elements in periodic group IA have oxidation numbers of +1, and elements in periodic group IIA have oxidation numbers of +2, e.g., Na+.
- The most electronegative element, fluorine, is always assigned both electrons from any bond in which it participates. This gives fluorine an oxidation number of –1 in all its compounds, e.g., OF2.
- Oxygen usually exhibits an oxidation number of –2, but exceptions occur in peroxides, superoxides, and when oxygen combines with fluorine.
- Hydrogen exhibits an oxidation number of +1 unless it is combined with an element more electropositive than itself, e.g., with lithium, in which case its oxidation number is –1.
- The sum of the oxidation numbers of all atoms in a complete formula must be 0; that is, when an electron is lost by one atom (+1 contribution to oxidation number), the same electron must be gained by another atom (–1 contribution to oxidation number).
- If a polyatomic ion is considered by itself, the sum of the oxidation numbers of its constituent atoms must equal the charge on the ion.
As an illustration of these rules, let us consider a few more examples.
Determine the oxidation number of each element in each of the following formulas: (a) NaClO; (b) ClO4–; and (c) MgH2.
Solution:
a) Since Na is a group IA element, its oxidation number is +1 (rule 3a). The oxidation number of O is usually –2 (rule 3c). Therefore (rule 4), +1 + oxidation number of Cl + (–2) = 0.
\[ \text{Oxidation number of Cl} = 2 – 1 = +1 \nonumber \]
Thus we write the formula
\[\overset{\text{+1}}{\mathop{\text{Na}}}\,\overset{+\text{1}}{\mathop{\text{Cl}}}\,\overset{-\text{2}}{\mathop{\text{O}}}\, \nonumber \]
if oxidation numbers are to be included.
b) In this case the oxidation numbers must add to –1, the charge on the polyatomic ion. Since O is usually –2, we have
\[ \text{Oxidation number of Cl} + 4(–2) = –1 \nonumber \]
\[ \text{Oxidation number of Cl} = –1 + 8 = +7 \nonumber \]
c) In MgH2, H is combined with an element more electropositive than itself, and so its oxidation number is –1. Mg is in group IIA,and so its oxidation number is +2:
\[\overset{\text{+2}}{\mathop{\text{Mg}}}\,\overset{-\text{1}}{\mathop{\text{H}}}\,_{\text{2}} \nonumber \]
As a check on these assignments, it is wise to make sure that the oxidation numbers sum to 0:
\[ +2 + 2(–1) = 0 \qquad \text{OK} \nonumber \]
Oxidation numbers are mainly used by chemists to identify and handle a type of chemical reaction called a redox reaction, or an oxidation-reduction reaction. This type of reaction can be recognized because it involves a change in oxidation number of at least one element. More information on these reactions is found in the section on redox reactions. Oxidation numbers are also used in the names of compounds. The internationally recommended rules of nomenclature involve roman numerals which represent oxidation numbers. For example, the two bromides of mercury, Hg2Br2 and HgBr2, are called mercury(I) bromide and mercury(II) bromide, respectively. Here the numeral I refers to an oxidation number of +1 for mercury, and II to an oxidation number of +2. Oxidation numbers can sometimes also be useful in writing Lewis structures, particularly for oxyanions. In the sulfite ion, SO32– for example, the oxidation number of sulfur is +4, suggesting that only four sulfur electrons are involved in the bonding. Since sulfur has six valence electrons, we conclude that two electrons are not involved in the bonding, i.e., that there is a lone pair. With this clue, a plausible Lewis structure is much easier to draw: