7.3: The Shapes of Molecules
- Page ID
- 49293
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The location in three-dimensional space of the nucleus of each atom in a molecule defines the molecular shape or molecular geometry. Molecular shapes are important in determining macroscopic properties such as melting and boiling points, and in predicting the ways in which one molecule can react with another. A number of experimental methods are available for finding molecular geometries, but we will not describe them here. Instead we will concentrate on several rules based on Lewis diagrams which will allow you to predict molecular shapes.
To provide specific cases which illustrate these rules, “ball-and stick” models for several different types of molecular geometries are shown in Table \(\PageIndex{1}\). The atoms (spheres) in each ball-and-stick model are held together by bonds (sticks). These electron-pair bonds determine the positions of the atoms and hence the molecular geometry.
| Formula A is central atom B is bonding atom N is unshared pair |
Shape | Structure Name | Example | Bond Angle (deg) |
|---|---|---|---|---|
| AB4 | 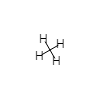 |
tetrahedral | 109 | |
| AB3N | .png?revision=1&size=bestfit&width=100&height=100) |
trigonal pyramidal | 109 | |
| AB3 | .png?revision=1&size=bestfit&width=100&height=100) |
trigonal planar | 120 | |
| AB2N2 | .png?revision=1&size=bestfit&width=70&height=70) |
bent | 109 | |
| AB2 | linear | 180 | ||
| AB2N |
.png?revision=1&size=bestfit&width=100&height=100)
|
bent | 120 | |
| AB5 | .png?revision=1&size=bestfit&width=100&height=100) |
triangular bipyrimidal | 120, 90 | |
| AB6 | .png?revision=1&size=bestfit&width=100&height=100) |
octahedral | 90 |
In each of the molecules shown in Table \(\PageIndex{1}\) the electron-pair bonds are arranged so that they avoid each other in space to the maximum possible extent. This may be understood in terms of the repulsion between electron clouds due to their like charges. During the 1950s the Australian R. S. Nyholm (1917 to 1971) and the Canadian R. J. Gillespie (1924 to ) summed up this behavior in terms of the valence-shell-electron-pair repulsion (VSEPR) theory. The VSEPR theory states that, because of their mutual repulsions, valence electron pairs surrounding an atom stay as far as possible from one another.
A simple model for demonstrating the behavior of electron pairs under the influence of their mutual repulsion is provided by a set of spherical balloons of equal size. It is a model that you can easily make for yourself. If, say, four balloons are tied together so that they squeeze each other fairly tightly, they inevitably adopt the tetrahedral arrangement shown for CH4 in Table \(\PageIndex{1}\). Although it is possible to flatten the balloons on a table until they are all in the same plane, they invariably spring back to the tetrahedral configuration as soon as the pressure is removed. Similar behavior is found if two, three, five, or six balloons are tightly tied together, except that in each case a different stable shape is adopted once the balloons are left to themselves.
Since all the shapes described in Table \(\PageIndex{1}\) constantly recur in chemical discussions, it is worth being able to recall them and their names without hesitation. To this end we will discuss the geometry of each of the five molecules. The table above has rotatable versions of each of these molecules. Use your mouse to rotate each of them as they are discussed.
- In BeH2 central Be atom has only two electron pairs in its valence shell. These are arranged on opposite sides of the Be atom in a straight line, and they bond the two atoms to the Be atom. Thus the three nuclei are all in a straight line, and the H―Be-H angle is 180°. A molecule such as BeH2, whose atoms all lie on the same straight line, is said to be linear. In BCl3 the three valence electron pairs, and hence the three Cl nuclei, are arranged in an equilateral triangle around the B atom. Each Cl―B―Cl angle is 120° and all four nuclei (B included) lie in the same plane. The three Cl atoms are said to be trigonally arranged around B.
- In CH4 the four H nuclei are at the four corners of a geometric figure called a tetrahedron. A tetrahedron has six equal edges, four equilateral triangular faces, and four identical corners (apices). The C nucleus lies in the exact center of the tetrahedron, equidistant from each corner. All the H—C—H angles are the same, namely, 109.5°. This important angle is called the tetrahedral angle. The four H atoms are said to be tetrahedrally arranged around the C atom. This tetrahedral arrangement is the most important of those described in Table 1.
- In PF5 the five F nuclei are arranged at the corners of a trigonal bi-pyramid. As drawn in the figure, one F atom lies directly above the P atom and one directly below. The remaining three F atoms are arranged in a triangle around the middle of the P. Some of the F―P―F angles are 90°, while others are 120°.
- In SF6 the six F atoms are arranged at the corners of an octahedron. An octahedron has twelve edges, eight equilateral triangular faces, and six identical corners. The name octahedron is derived from the eight faces, but it is usually the six corners of this figure which are of interest to chemists. Thus you will have to remember that an octahedral arrangement involves six atoms, not the eight that the name seems to imply.
- In SF6 the six F atoms are octahedrally arranged around the S. All the F―S―F angles are 90°. Octahedral arrangements are quite common in chemistry. In crystals of LiH and NaCl, for instance, six anions are arranged octahedrally around each cation while six cations are arranged octahedrally around each anion.


