14.3: Redox Reactions and Titrations
- Page ID
- 134631
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Define oxidation, reduction, oxidizing agent and reducing agent.
- Define oxidation state and oxidation number.
- Have a knowledge of the oxidation state rules and assign oxidation numbers to atoms in molecules and ions.
- Identify a redox reaction by assigning oxidation numbers to each element.
- Write the oxidation and reduction half reactions for a redox reaction.
- Distinguish between a redox reaction and a non-redox reaction.
- Write balanced Oxidation/Reduction Equations.
- Apply the Nernst equation in all directions to determine missing quantities.
- Describe and discuss Redox titrations.
- Carry out redox-type titrations and associated calculations.
Summary of learning activity #3
Chemical reactions in which there is a transfer of electrons from one substance to another are known as oxidation-reduction reactions or redox reactions. In this unit, we will consider the class of reactions called oxidation-reduction, or redox and examine the oxidation-reduction process and use the oxidation state and oxidation number concepts to not only identify redox reactions but also keep track of electrons transferred in a chemical reaction. The introductory sections of the unit explains the fundamental principles of galvanic cells, the thermodynamics of electrochemical reaction. Some applications of the concept of redox equilibria in explaining oxidation-reduction titrations as a technique for volumetric chemical analysis are also discussed.
Key Concepts
- Nernst equation: relates the electrochemical potential to the concentration of reactants and products participating in a redox reaction.
- Oxidation: theprocessbywhichacompoundloosesorappearstolooseelectrons. It corresponds to an increase in the oxidation number.
- Oxidizing agent: species that causes oxidation. An oxidizing agent accepts electrons from the species it oxidizes and therefore, an oxidizing agent is alwaysreduced.
- Oxidation number: these are used to keep track of electron transfer. Oxidation numbers are assigned to ionic as well as molecular compounds. Oxidation numbers are assigned per atom.
- Oxidation reaction:refers to the half-reaction that involves loss of electrons.
- Redox reactions: these are or oxidation-reduction reactions that involve trans- fer of electrons. As the electron transfer occurs, substances undergo changes inoxidation number.
- Reduction: the process by which a compound gains or appears to gain electrons. It corresponds to a decrease in oxidation number.
- Reduction reaction: is a half-reaction that involves gain of electrons.Reducing agent: species that causes reduction. A reducing agent donates electrons to the species it reduces and therefore, a reducing agent is always oxidized.
Introduction to activity # 3
Oxidation-reduction (redox) reactions or processes are very much a part of the world that we live in. These processes or reactions range from the burning of fossil fuels to the action of the oxidizing power of sodium hypochlorite, the active ingredient in household bleach. It is very likely that all of us have at one time or another come across atleast a process or feature that is as a result of a redox process. It is very probable that we have seen many examples of corrosion around us such as rust on iron, tarnish on silverware, and the greening on copper or brass surfaces or material. All these changes that we observe on almost day to day basis without thinking of their chemical origin or nature are examples of processes resulting from redox reactions. Most metallic and nonmetallic elementswhich find important uses in modern day world, are obtained from their ores bythe process of oxidation or reduction reactions.All of these examples are some of the consequences of oxidation-reduction reactions. These are basically reactions that involve electron-transfer. Oxidation-reduction analysis has been used over the years as an alternate method of analyzing for materials that have multiple oxidation states. This unit in part, will help us to link what is happening at the submicroscopic level to macroscopic events in electrochemistry that we see.
List of other compulsory readings
A text that contains vital information on the Nernst Equation, the significance ofthe equation and analytical applications in quantitative analysis of metal ions in solution (Reading #24)
A text on “Redox Equilibria in Natural Waters” (Reading #25)
A text with sub-sections containing sample problems dealing with chemical equilibrium, oxidation-reduction reactions (Reading #13)
Balancing Redox Equations by Using Half-reactionsBalancing Redox Equations (Reading # 26)
Oxidation NumbersRules for Oxidation Numbers (Reading #27) Reactions in Aqueous solutions (Reading #28)
Balance redox (Reading #29)
List of relevant resources
List of relevant useful links
http://www.chemguide.co.uk/inorganic...xmenu.html#top
http://www.chemguide.co.uk/physical/...tions.html#top
www.voyager.dvc.edu/~Iborowsk...RedoxIndex.htm
Detailed description of activity #3
Redox (Reduction – Oxidation) Reactions
Introduction: Chemical reactions involve the exchange of electrons between two or more atoms or molecules. The species involved, exchange electrons which, leads to a change in the charge of both the atoms of that species. This change in the charges of atoms (change in the atom’s oxidation number) by means ofelectron exchange is defined as a Reduction-Oxidation (Redox) reaction. Che- mists usually use the terms oxidizing and reducing agents to describe the reac- tants in redox reactions. Because oxidation is the process of losing electrons, an oxidizing agent is defined simply as any substance that can cause a loss of electronsinanothersubstanceinachemicalreaction. Thus,anoxidizingagentgains electrons, and its oxidation number (a positive or negative number which represents the oxidation state of an atom as defined below) thereby decreases.Reduction on the other hand, is the process of gaining electrons and therefore areducing agent is a substance that can cause another substance to gain electrons. The reducing agent therefore loses electrons, and its oxidation number thereby increases. Therefore, as a reducing agent reduces the other reagent, it is itself being oxidized. Conversely, as an oxidizing agent oxidizes the other reagent, it is itself being reduced.
To keep track of electrons in redox reactions, it is useful to assign oxidation num- bers to the reactants and products. An atom’s oxidation number, also referred to as oxidation state, signifies the number of charges the atom would have in a molecule (or an ionic compound) if electrons were transferred completely.
For example, we can write equations for the formation of HCl and SO2 as follows:
0 0 + -1
H2 (g) + Cl2 (g) → 2HCl (g)
0 0 +4 -2
S (s) + O2 (g) → SO2 (g)
The numbers above the elements symbols are the oxidation numbers. In both of the reactions shown, there is no charge on the atoms in the reactant molecu- les. Thus their oxidation number is zero. For the product molecules, however, it is asumed that complete electron transfer has taken place and that atoms havegained or lost electrons. The oxidation numbers reflect the number of electrons“transferred”.
Oxidation numbers enables us to identify elements that are oxidized and reduced at a glance. The elements that show an increase in oxidation number- hydrogen and sulfur in the preceding examples – are oxidized. Chlorine and oxygen are reduced, so their oxidation numbers show a decrease from their initial values. Note that the sum of the oxidation numbers of H and Cl in HCl (+1 and -1) is zero. Likewise, if we add the charges on S (+4) and two atoms of O [2 x (-2)], the total is zero. The reason is that the HCl and SO2 molecules are neutral, so the charges must cancel.
The following rules are used by chemists to assign oxidation numbers:
- In free elements (i.e., in the uncombined state), each atom has an oxidation number of zero. Thus each atom in H2, Br2, Na, K, O2 and P4 has the same oxidation number: zero.
- For ions composed of only one atom (i.e., monoatomic ions) the oxidation number is equal to the charge on the ion. Thus Li+ ion has an oxidation number of +1, Ba2+ ion, +2; Fe3+, +3; I- ion, -1; O2- ion, -2; etc. All alkali metals have an oxidation number of +1 and all alkaline earth metals have an oxidation number of +2 in their compounds. Aluminum has an oxidation number of +3 in all its compounds.
- The oxidation number of oxygen in most compounds (e.g., MgO and H2O) is -2, but in hydrogen peroxide (H2O2) and peroxide ion (O22-), it is -1.
- The oxidation number of of hydrogen is +1, except when it is bonded to metals in binary compounds. In these case (for example, LiH, NaH, CaH2), its oxidation number is -1.
- Fluorine has an oxidation number of -1 in all its compounds. Other halogens (Cl, Br, and I) have negative oxidation numbers when they occur as halide ions in their compounds. When combined with oxygen – for example in oxoacids and oxoanions – they have positive oxidation numbers.
- In a neutral molecule, the sum of the oxidation numbers of all the atoms must be zero. In a polyatomic ion, the sum of oxidation numbers of all the elements in the ion must be equal to the net charge of the ion. For example, in the ammonium ion, NH4+, the oxidation number of N is -3
and that of H is +1. the sum of the oxidation numbers is -3 + 4(+1) = +1, which is equal to the net charge of the ion. - Oxidation numbers do not have to be integers. For example, the oxidation number of O in the superoxide ion O2-, is -1/2.
Using the rules above, assign oxidation numbers to all the elements in the following compounds and ion: (a) Li2O, (b) HNO3, (c) Cr2O22-
Solution
- By rule 2, we see that lithium has an oxidation number of +1 (Li+) and oxygen’s oxidation number is -2 (O2-).
- HNO3 yields H+ and NO3- ion in solution. From rule 4 we see that H has an oxidation number of +1. Thus the other group (nitrate ion) must have a net oxidation number of -1. Oxygen has an oxidation number of -2, and if we use x to represent the oxidation number of nitrogen, then the nitrate ion can be written as: [N(x) O3(2-)]- so that x + 3(-2) = -1 or x = +5
- From Rule 6, we see that the sum of the oxidation numbers in the dichromate ion Cr2O72- must be -2. We know that the oxidation number of O is -2, so all that remains is to determine the oxidation number of Cr, which we can call y. the dichromate ion can be written as: [Cr2(y) O7(2-)]2- so that 2(y) + 7(-2) = -2 or y = +6.
Assign oxidation numbers to all the elements in the following anions (a) NO3-, (b) MnO4- (c) SbCl5
- Answer
Question : How does one tell a redox reaction from an ion exchange reaction? How does one know that electron transfer has taken place?
Answer: Electron transfer is manifested in change in oxidation number or oxi- dation state. We know electron transfer has taken place if the oxidation number of an element has changed.
(The numbers written above the symbols are their corresponding oxidation states)
- +1 +5 -2 +2 -1 +1 -1 +2 +5 -2
2 AgNO3 (aq) + CuCl2 (aq) → 2 AgCl (s) + Cu(NO3)2 (aq)
- +1 +5 -2 0 0 +2 +5 -2
2 AgNO3 (aq) + Cu (s) → 2 Ag (s) + Cu(NO3)2 (aq)
Which of the two reactions is a redox reaction? Explain!
Solution: (b) is a redox reaction since reaction involves electron transfer. Note that the oxidation state of Cu has moved from zero to +2, while that of Ag has changed from +1 to zero. Ag+ is the oxidizing agent (it gains an electron) while Cu is the reducing agent (it loses two electrons).
Which is the reducing agent in the following reaction?
2 VO + 3Fe3O4 →
V2O5 + 9 FeO
- Answer
Balancing of a Redox Reaction
The rules for balancing half reactions are the same as those for ordinary reactions;that is, the number of atoms of each element as well as the net charge on both sides of the equation must be equal.
The following are the steps for balancing a Redox reaction:
- Identify the species being oxidized and the species being reduced.
- Write the oxidation and reduction half-reactions. For each half-reaction:
- Solution:
Step 1: Determine the oxidation state for every atom in the skeleton equationabove.
Balance the elements except for O and H.
- Balance the number of electrons gained or lost.
- Balance the net charges by adding H+ (acidic) or OH- (basic).
- Balance the O and H by adding H2O.
- Solution:
Strategy for balancing redox reactions in acidic solutions:
Balance the equation for the reaction between dilute nitric acid and copper metal leading to the production of copper ions and the gas nitric oxide, NO given below:
Cu(s) + H+ (aq) + NO3- (aq) → Cu2+ (aq) + NO(g)
Solution
Step 1: Determine the oxidation state for every atom in the skeleton equation above.
0 +1 +5 -2 +2 +2-2
Cu(s) + H+ (aq) + NO3- (aq) → Cu2+ (aq) + NO(g)
Changes in Oxidation status:
CU: 0 → +2 Oxidation
N: +5 → +2 Reduction
Step 2: Write the skeleton half reactions.
Oxidation: Cu → Cu2+
Reduction: NO3- → NO
Step 3: Balance each half-reaction “atomically).
- consider all atoms other than H and O (use any of the species that appear in the skeleton equation of step 1 above)
- balance O atoms by adding H2O
- balance H atoms by adding H+
Oxidation: Cu → Cu2+
Reduction: NO3- → NO + 2H2O
Reduction: NO3- + 4H+ → NO + 2H2O
Step 4: Balance the electric charges by adding electrons (electrons have to appear on the right hand side of the oxidation half-reaction and on the left hand side of the reduction half-reaction).
Oxidation: Cu → Cu2+ + 2e-
Reduction: NO3- + 4H+ + 3e- → NO + 2H2O
Step 5: Make the number of electrons the same in both the half reactions by findingthe least common multiple as we prepare to sum the two half equations.
i.e., 3 x Oxidation reaction: 3Cu → 3Cu2+ + 6e-
and 2 x Reduction reaction: 2NO3- + 8H+ + 6e- → 2NO + 4H2O
Step 6: Now combine the two half-reactions.
3Cu + 2NO3 - + 8H+ + 6e- → 3Cu2+ + 6e- + 2NO + 4H2O
Step 7: Simplify the summation.
3Cu + 2NO3 - + 8H+ → 3Cu2+ + 2NO + 4H2O
Step 8: Indicate the state of each species to obtain the fully balanced net ionic equation.
3Cu(s) + 2NO3 - (aq) + 8H+ (aq) → 3Cu2+ (aq) + 2NO (aq) + 4H2O (l)
Strategy for redox reactions in basic solutions: (First balance the reaction as though it was in acid (use H+ to balance hydrogen atoms)
Example 2: Balance the equation NO3- + Al → NH3 + Al(OH)4- in basic solution.
Solution
Step 1: Write the skeleton equation and determine the oxidation state per atom.
+5 -2 0 +3 -1 +3 -2 -1
NO3- + Al → NH3 + Al(OH)4-
Al is being oxidized. Its oxidation number changes from 0 to +3
N in NO3 - is being reduced. Its oxidation number changes from +5 to +3
Changes in Oxidation status:
Al: 0 → +3 Oxidation
N: +5 → +3 Reduction
Step 2: Write the skeleton half reactions.
Oxidation: Al → Al(OH)4 -
Reduction: NO3 - → NH3
Step 3: Balance each half-reaction “atomically).
NOTE: In basic solutions, no H+ are available to balance H. Hence, we pretend that the solution is acidic and carry out a neutralization reaction at the end.
As was the case with acidic solution above,
- consider all atoms other than H and O (use any of the species that appear in the skeleton equation of step 1 above)
- balance O atoms by adding H2O
- balance H atoms by adding H+
Oxidation: Al + 4H2O → Al(OH)4 -
Oxidation: Al + 4H2O → Al(OH)4- + 4H+
Reduction: NO3- → NH3 + 3H2O
Reduction: NO3- → 9H+ → NH3 + 3H2O
Step 4: Balance the electric charges by adding electrons (electrons have to appear on the right hand side of the oxidation half-reaction and on the left hand side of the reduction half-reaction).
Oxidation: Al + 4H2O → Al(OH)4 - + 4H+ + 3e-
Reduction: NO3- + 9H+ + 8e- → NH3 + 3H2O
Step 5: Make the number of electrons the same in both the half reactions by findingthe least common multiple as we prepare to sum the two half equations.
i.e., 8 x Oxidation reaction: 8Al + 32H2O → 8Al(OH)4 - + 32H+ + 24e-
and 3 x Reduction reaction: 3NO3 - + 27H+ + 24e- → 3NH3 + 9H2O
Step 6: Now combine the two half-reactions.
8Al + 32H2O + 3NO3- + 27H+ + 24e- → 8Al(OH)4- + 32H+ + 24e- + 3NH3 + 9H2O
Step 7: Simplify the summation.
8Al + 23H2O + 3NO3 - → 8Al(OH)4 - + 3NH3 + 5H+
Step 7b: Change to basic solution by adding as many OH- to both sides as there are H+.
8Al + 23H2O + 3NO3- + 5OH- → 8Al(OH)4 - + 3NH3 +5H+ + 5OH-
Neutralization procedure: Combine the H+ and the OH- to form H2O.
8Al + 3NO3- + 23 H2O + 5OH - → 8Al(OH)4- + 3NH3 + 5H2O
Now simplify: (by cancelling out redundant H2O molecules from each side)
8Al + 3NO3- + 18H2O + 5OH - → 8Al(OH)4- + 3NH3
Step 8:Indicate state of each species
8Al(s) + 3NO3- (aq) + 18H2O(l) + 5OH- (aq) → 8Al(OH)4-(aq) + 3NH3 (g)
This is the fully balanced net ionic equation.
Balance the following reaction that occurs in basic solution. Write complete, balanced equations for the oxidation and reduction half-reactions and the net ionic equation.
N2H4 + BrO3- → NO + Br-
Solution
Step 1: Check the oxidation numbers to determine what is oxidized and what is reduced.
Bromine goes from +5 in BrO3- to -1 in Br-. Thus BrO3- is being reduced.
Nitrogen goes from -2 in N2H4 to +2 in NO. Hence N2H4 is being oxidized.
The unbalance half-reactions are:
Oxidation: N2H4 → NO
Reduction: BrO3- → Br-
Step 2: Balance atoms other than H and O:
Oxidation: N2H4 → 2NO
Reduction: BrO3- → Br-
Step 3: Balance O with H2O and then H with H+.
Oxidation: 2H2O + N2H4 → 2NO + 8H+
Reduction: 6H+ + BrO3 - → Br- + 3H2O
(Now the atoms are balanced but the charges are not)
Step 4:Balance the charge with electrons.
Oxidation: 2H2O + N2H4 → 2NO + 8H+ + 8e-
Reduction: 6H+ + BrO3- + 6e- → Br- + 3H2O
Step 5: Make the number of electrons the same in both the half reactions by findingthe least common multiple as we prepare to sum the two half equations.
3 x Oxidation: 6H2O + 3N2H4 → 6NO + 24H+ + 24e-
4 x Reduction: 24H+ + 4BrO3- + 24e- → 4Br- + 12H2O
Step 6: Now combine the two half-reactions.
6H2O + 3N2H4 + 24H+ + 4BrO3- + 24e- → 6NO + 24H+ + 24e- + 4Br- + 12H2O
Step 7:Simplify the summation.
3N2H4 + 4BrO3- → 6NO + 4Br- + 6H2O
Step 8: Indicate state of each species
3N2H4 (g) + 4BrO3- (aq) → 6NO (g) + 4Br- (aq) + 6H2O (l)
This is the fully balanced net ionic equation.
Balance the equation: I- + Br2 → IO3- + Br- in acidic solution.
Oxidation: 3H2O + I- → IO3- + 6e- + 6H+
Reduction: Br2 + 2e- → 2Br-
Overall: 3Br2 + I- + 3H2O → 6Br- + IO3- + 6H+
- Answer
Redox Titrations
Redox titration is a titration in which the reaction between the analyte and titrant is an oxidation/reduction reaction. Like acid-base titrations, redox titrations normally require an indicator that clearly changes colour. In the presence of large amounts of reducing agent, the colour of the indicator is characteristic of its reduced form. The indicator normally assumes the colour of its oxidized form when it is present in an oxidizing medium. At or near the equivalence point, a sharp change in the indicator’s colour will occur as it changes from one form to the other, so the equivalence point can be readily identified.
Since all redox titrations involve the flow of electrons, all redox titrations can bemonitored by looking at the electrical potential of the solution. All one needs to monitor the potential of a solution is a reference electrode and an inert electrode. The details of the workings of such a setup is however, outside the scope of this unit and will not be covered. Nevertheless, the relevant expression that utilizes the experimentally measurable elctrochemical potential, E as a function of titrant volume will be discussed later.
Titrimetic methods that are based on the use of the principles of redox reactionshave been used widely in the determination of metals which have two well-definedoxidation states. The process of analysis often involves either:
(i) converting all the metal ions to be analysed (analyte) to a higher oxidation state by use of an oxidizing agent such as sodium peroxide and sodium bismuthate, or
(ii) converting all the analyte metal ions to a lower oxidation state by using a reducing agent such as sulphur dioxide or sodium bisulphite.
In both situations, an excess of reagent is needed which is then destroyed or removed before the sample is titrated.
There are other ways of carrying out quantitative reduction experiments but these are outside the scope of this Unit and will not be covered here.
Redox Titration Curves
To evaluate a redox titration we must know the shape of its titration curve. In an acid–base titration (see previous unit) or a complexation titration (see unit 4), a titration curve shows the change in concentration of hydronium ions, H3O+ (as pH) or Mn+ (as pM) as a function of the volume of titrant. For a redox titration,
it is convenient to monitor electrochemical potential. Nernst equation, which relates the electrochemical potential to the concentration of reactants and products participating in a redox reaction is often used in determining the concentration of an analyte. Consider, for example, a titration in which the analyte in a reduced state, Ared, is titrated against a titrant in an oxidized state, Tox. The titration reaction can therefore be expressed as:
Ared + Tox ⇌ Tred + Aox
The corresponding electrochemical potential for the reaction, Erxn, is the difference between the potentials for the reduction and oxidation half-reactions; i.e.,
$$\bf{E}_{rxn}=\bf{E}_{Tox/Tred}-\bf{E}_{Aox}$$
During the titration process, upon each addition of titrant, the reaction between the analyte and titrant reaches a state of equilibrium. Under these equilibrium conditions, the reaction’s electrochemical potential, Erxn, becomes zero, and
\[\bf{E}_{Tox/Tred}=\bf{E}_{Aox/Ared}\]
This is true since the two redox systems we are titrating together are in equili- brium and hence the potential of the two pairs are equal. Thus, the potential of the reactant mixture can be found by calculating the electrochemical potential, E for either of the redox pairs.
Consequently, the electrochemical potential for either half-reaction may beused to monitor the titration’s progress.
It is significant to note that before the equivalence point is reached during thecourse of the titration process, the resultant mixture consists of appreciable quantities of both the oxidized (Aox) and reduced (Ared) forms of the analyte, but very little unreacted titrant. The potential, therefore, is best calculated using the Nernst equation for the analyte’s half-reaction. Although E°Aox /Ared is the standard-state potential for the analyte’s half-reaction, a matrix-dependent formal potential,the potential of a redox reaction for a specific set of solution conditions, such aspH and ionic composition, is used in its place.
Illustration of How to Calculate a Redox Titration Curve
Let us calculate the titration curve for the titration of 50.0 mL of 0.100 mol/L Fe2+ with 0.100 mol/L Ce4+ in a matrix of 1 mol/L HClO . The reaction in
this case is
Fe2+(aq) + Ce4+(aq) ⇌ Ce3+(aq) + Fe3+(aq)
The equilibrium constant for this reaction is quite large (it is approximately 6x1015), so we may assume that the analyte and titrant react completely.
The first task in calculating the titration curve is to calculate the volume of Ce4+needed to reach the equivalence point. From the stoichiometry of the reaction we know that
Number of moles of Fe2+ = number of moles of Ce4+ or
MFeVFe = MCeVCe
where MFe is the concentration of Fe2+ and VFe is the volume of solution of Fe2+; and MCE is the concentration of Ce4+ and VCe is the volume of solution of Ce4+. Solving for the volume of Ce4+ gives the equivalence point volume as 50.0 mL (i.e., VCe = MFeVFe / MCe).
Before the equivalence point the concentration of unreacted Fe2+ and the concentration of Fe3+ produced by the reaction are easy to calculate. For this reason we find the electrochemical potential, E using the Nernst equation for the analyte’s half-reaction
\[
\mathrm { E } = \mathrm { E } _ { \mathrm { Fe } ^ { 3 + } / \mathrm { Fe } ^ { 2 + } } ^ { 0 } - 0.05916 \log \frac { \left[ \mathrm { Fe } ^ { 2 + } \right] } { \left[ \mathrm { Fe } ^ { 3 + } \right] }
\nonumber\]
Illustration:
The concentrations of Fe2+ and Fe3+ in solution after adding 5.0 mL of titrant (i.e., Ce4+ solution) are:
\(\
\left[ \mathrm { Fe } ^ { 2 + } \right] = \frac { \text { moles of unreacted } \mathrm { Fe } ^ { 2 + } } { \text { total volume } } = \frac { \mathrm { M } _ { \mathrm { Fc } } \mathrm { V } _ { \mathrm { Fe } } - \mathrm { M } _ { \mathrm { Ce } } \mathrm { V } _ { \mathrm { Ce } } } { \mathrm { V } _ { \mathrm { re } } + \mathrm { V } _ { \mathrm { ce } } } = \frac { ( 0.100 \times 50 ) - ( 0.100 \times 5 ) } { ( 50 + 5 ) } = 8.18 \times 10 ^ { - 2 } \mathrm { M }
\nonumber\)
\(\
\left[ \mathrm { Fe } ^ { 3 + } \right] = \frac { \text { moles of } \mathrm { Ce } ^ { 4 + } \text { added } } { \text { total volume } } = \frac { \mathrm { M } _ { c e } \mathrm { V } _ { \mathrm { ce } } } { \mathrm { V } _ { \mathrm { Fe } } + \mathrm { V } _ { \mathrm { ce } } } = 9.09 \times 10 ^ { - 3 } \mathrm { mol } / \mathrm { L }
\nonumber\)
Substituting these concentrations into the Nernst equation for Fe along with the formal potential for the Fe3+/Fe2+ half-reaction from a table of reduction potentials,we find that the electrochemical potential is:
\(\
\mathrm { E } = + 0.767 \mathrm { V } - 0.05916 \log \left( \frac { 8.18 \times 10 ^ { - 2 } } { 9.09 \times 10 ^ { - 3 } } \right) = + 0.711 \mathrm { V }
\)
Similar electrochemical potential calculations can be carried out for various volumes of titrant (Ce4+) added.
At the equivalence point, the moles of Fe2+ initially present and the moles of Ce4+added become equal. Now, because the equilibrium constant for the reaction is large, the concentrations of Fe2+ and Ce4+ become exceedingly small and difficultto calculate without resorting to a complex equilibrium problem. Consequently, we cannot calculate the potential at the equivalence point, Eeq using just the Nernst equation for the analyte’s half-reaction or the titrant’s half-reaction. We can, however, calculate Eeq by combining the two Nernst equations. To do so we recognize that the potentials for the two half-reactions are the same; thus,
\(\
\mathrm { E } _ { \mathrm { eq } } = \mathrm { E } _ { \mathrm { Fe } ^ { 3+ }/ \mathrm { Fe } ^ { 2 + } } ^ { 0 } - 0.05916 \log \frac { \left[ \mathrm { Fe } ^ { 2 + } \right] } { \left[ \mathrm { Fe } ^ { 3 + } \right] } \mathrm { and }
\)
\(\
\mathrm { E } _ { \mathrm { eq } } = \mathrm { E } _ { \mathrm { ce } ^ { 4 }/ \mathrm { Ce } ^ { 3 + } } ^ { 0 } - 0.05916 \log \frac { \left[ \mathrm { Ce } ^ { 3 + } \right] } { \left[ \mathrm { Ce } ^ { 4 + } \right] }
\)
Adding the two Nernst equations yields
\(\
2 \mathrm { E } _ { \mathrm { eq } } = \mathrm { E } _ { \mathrm { Fe } ^ { 3 + }/ \mathrm { Fe } ^ { 2 + } } ^ { 0 } + \mathrm { E } _ { \mathrm { Ce } ^ { 4 + } / \mathrm { ce } ^ { 3 + } } ^ { 0 } - 0.05916 \log \frac { \left[ \mathrm { Fe } ^ { 2 + } \right] \left[ \mathrm { Ce } ^ { 3 + } \right] } { \left[ \mathrm { Fe } ^ { 3 + } \right] \left[ \mathrm { Ce } ^ { 4 + } \right] }
\)
At the equivalence point, the titration reaction’s stoichiometry requires that
[Fe2+] = [Ce4+] and [Fe3+] = [Ce3+]
This will make the log term in the above equation equals zero. The equationsimplifies to
\(\ \bf{E}_{eq}={\bf{E^o}_{Fe^{3+}/{Fe^{2+}}}+\bf{E^o}_{Ce^{4+}/Ce^{3+}}\over 2 }={0.767V+1.70V\over 2}=1.23\)
After the equivalence point, the concentrations of Ce3+ and excess Ce4+ are easy to calculate. The potential, therefore, is best calculated using the Nernst equation for the titrant’s half-reaction,
\(\
\mathrm { E } = \mathrm { E } _ { \mathrm { ce } ^ { 4 + } / \mathrm { ce } ^ { 3 + } } ^ { 0 } - 0.05916 \log \frac { \left[ \mathrm { Ce } ^ { 3 + } \right] } { \left[ \mathrm { Ce } ^ { 4 + } \right] }
\)
Illustration:
After adding 60.0 mL of titrant, the concentrations of Ce3+ and Ce4+ are
\(\
[\mathrm {Ce^{3+}}]={initial\ moles\ \mathrm{Fe^{2+}}\over total\ volume}={\bf{M}_{Fe}\bf{V}_{Fe}\over{\bf{V}_{Fe}+\bf{V}_{Ce}}}={(0.100\ mol/L)(50.0\ mL)\over 50.0\ mL \ +\ 60.0\ mL }=4.55x10^{-2}\ mol/L
\)
\(\
[\mathrm{Ce}^{4+}]={moles\ of\ excess\ \mathrm{Ce}^{4+}\over total\ volume}={\bf{M}_{Ce}\bf{V}_{Ce}\ -\ \bf{M}_{Fe}\bf{V}_{Fe}\over \bf{V}_{Fe}\ +\ \bf{V}_{Ce}}={(0.100\ mol/L)(60.0\ mL)\ -\ (0.100\ mol/L)(50.0\ mL)\over 50.0\ mL\ +\ 60.0\ mL}
\)
Substituting these concentrations into the Nernst equation for Ce4+/Ce3+ half- reaction equation gives the potential as
\(\
\mathrm { E } = + 1.70 \mathrm { V } - 0.05916 \log \frac { 4.55 \times 10 ^ { - 2 } } { 9.09 \times 10 ^ { - 3 } } = 1.66 \mathrm { V }
\)
Additional data for the plot of the titration curve can be generated following the same procedure above.
How to Sketch a Redox Titration Curve using minimum number of calculations:
Sketch a titration curve for the titration of 50.0 mL of 0.100 mol/L Fe2+ with 0.100 mol/L Ce4+ in a matrix of 1 M HClO4.
Solution
This is the same titration that we previously calculated the titration curve for.
We begin as usual, by drawing the axes for the titration curve Potential E versus volume of titrant added in mLs. Having shown that the equivalence point volume is 50.0 mL, we draw a vertical line intersecting the x-axis at this volume.
Before the equivalence point, the solution’s electrochemical potential is calculated from the concentration of excess Fe2+ and the concentration of Fe3+ produced by the titration reaction. Using tabulated values of the matrix-dependent formal potential values, we can now calculate the corresponding electrochemical potential values E and plot E for 5.0 mL and 45.0 mL of titrant in the graph.
After the equivalence point, the solution’s electrochemical potential is determined by the concentration of excess Ce4+ and the concentration of Ce3+. Using tabulated values of the matrix-dependent formal potential values, we can now calculate the corresponding electrochemical potential values E and again plot points for 60.0 mL and 80.0 mL of titrant.
To complete an approximate sketch of the titration curve, we draw separate straight lines through the two points before and after the equivalence point. Finally, a smooth curve is drawn to connect the three straight-line segments.
Selecting and Evaluating the End Point
The equivalence point of a redox titration occurs when stoichiometrically equivalent amounts of analyte and titrant react. As with other titrations, any difference between the equivalence point and the end point is a determinate (see unit 1) source of error.
The most obvious question to ask is: Where is the Equivalence Point?
Previously, in discussing acid–base titrations, we noted that the equivalence pointis almost identical with the inflection point located in the sharply rising part of anytitration curve. When the stoichiometry of a redox titration is symmetrical (i.e., one mole analyte per mole of titrant), then the equivalence point is equally sym-metrical. If however, the stoichiometry is not symmetrical, then the equivalence point will lie closer to the top or bottom of the titration curve’s sharp rise. In this case the equivalence point is said to be asymmetrical. The following example shows how to calculate the equivalence point potential in this situation.
Derive a general equation for the electrochemical potential at the equivalence point for the titration of Fe2+ with MnO4- . The stoichiometry of the reaction is such that
5Fe2+(aq) + MnO4- (aq) + 8H3O+ (aq) ⇌5Fe3+ (aq) + Mn2+(aq) + 12H2O(l)
Solution
The redox half-reactions for the analyte and the titrant are:
Fe2+(aq)⇌ Fe3+(aq) + e–
MnO4- (aq) + 8H3O+(aq) + 5e- ⇌ Mn2+(aq) + 12H2O(l)
for which the corresponding Nernst equations are:
\(\
\mathrm { E } _ { \mathrm { eq } } = \mathrm { E } _ { \mathrm { Fe } ^ { 3 + }/ \mathrm { Fe } ^ { 2 + } } ^ { 0 } - 0.05916 \log \frac { \left[ \mathrm { Fe } ^ { 2 + } \right] } { \left[ \mathrm { Fe } ^ { 3 + } \right] }
\)
\(\
\mathrm { E } _ { \mathrm { eq } } = \mathrm { E } _ { \mathrm { MnO }_4 ^ { - }/ \mathrm { Mn } ^ { 2 + } } ^ { 0 } - {0.05916\over 5} \log \frac { \left[ \mathrm { Mn } ^ { 2 + } \right] } { \left[ \mathrm { MnO }_4 ^ { - } \right]\left[ \mathrm { H_3O } ^ { + } \right]^8 }
\)
Before adding together these two equations, the second equation must be multi-plied by 5 so that the log terms can be combined; thus at the equivalence point,we know that
[Fe2+] = 5 x [MnO4- ]
[Fe3+] = 5 x [Mn2+]
Substituting these equalities into the equation for Eeq and rearranging gives
\(\
\bf{E}_{eq}={\bf{E}_{Fe^{3+}/Fe^{2+}}^0\ +\ \bf{5E}_{\bf{MnO}_4^-/Mn^{2+}}^0\over 6}-{0.05916\over 6}log{5[\bf{MnO}_4^-][Mn^{2+}]\over 5[Mn^{2+}][\bf{MnO}_4^-][\bf{H}_3O^+]^8}
\)
\(\
={\bf{E}_{Fe^{3+}/Fe^{2+}}^0\ +\ \bf{5E}_{\bf{MnO}_4^-/Mn^{2+}}\over 6}-{0.05916\over 6}log{1\over [\bf{H}_3O^+]^8}
\)
\(\
={\bf{E}_{Fe^{3+}/Fe^{2+}}^0\ +\ \bf{5E}_{\bf{MnO}_4^-/Mn^{2+}}\over 6}+{(0.05916)(8)\over 6}log [\bf{H}_3O^+]
\)
\(\
={\bf{E}_{Fe^{3+}/Fe^{2+}}^0\ +\ \bf{5E}_{\bf{MnO}_4^-/Mn^{2+}}\over 6}-0.0788pH
\)
For this titration, the electrochemical potential at the equivalence point consistsof two terms: The first term is a weighted average of the standard state orformal potentials for the analyte and titrant, in which the weighting factors are the number of electrons in their respective redox half-reactions. The second term shows that Eeq is pH-dependent. The Figure below shows a typical titration curve for the analysis of Fe2+ by titration with MnO4-, showing the asymmetrical equivalence point. Note that the change in potential near the equivalence point is sharp enough that selecting an end point near the middle of the titration curve’ssharply rising portion does not introduce a significant titration error.
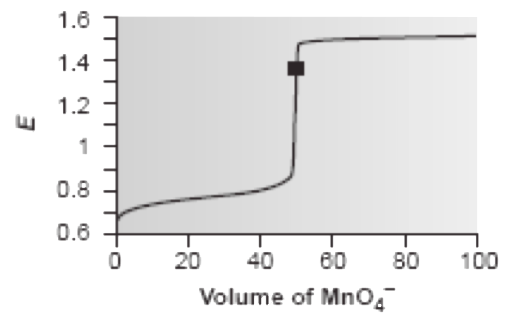
Figure: Titration curve for Fe2+ with MnO4- in 1 mol/L H2SO4 . The equivalence point is shown by the symbol •.
Detection of End Point:
The end point of a redox titration can be determined by either an electrode via measuring the electrochemical potential with an indicating electrode relative to a reference electrode and plotting this electrochemical potential against the volume of titrant or by a colour indicator. However, as in other titrations, it is usually more convenient to use visual indicators.
Finding the End Point with a Visual Indicator
There are three methods used for visual indication of the end point in a redox titration. These are:
A. Self-Indication: A few titrants, such as MnO4-, have oxidized and reduced forms whose colors in solution are significantly different: Solutions of MnO4- are intensely purple. In acidic solutions, however, the reduced form of permanganate, Mn2+, is nearly colourless. When MnO4- is used as an oxidizing titrant, the solution remains colourless until the first drop of excess MnO4- is added. The first permanent tinge of purple signals the end point.
B. Starch Indicator: A few substances indicate the presence of a specific oxidized or reduced species. Starch, for example, forms a dark blue complex with I3- and can be used to signal the presence of excess I3- (color change: colourless to blue), or the completion of a reaction in which I3- is consumed (color change:blue to colourless). Another example of a specific indicator is thiocyanate, whichforms a soluble red-colored complex, Fe(SCN)2+, with Fe3+.
C. Redox Indicators: The most important class of visual indicators, however, are substances that do not participate in the redox titration, but whose oxidized and reduced forms differ in color. When added to a solution containing the ana- lyte, the indicator imparts a color that depends on the solution’s electrochemical potential. Since the indicator changes color in response to the electrochemicalpotential, and not to the presence or absence of a specific species, these compoundsare called general redox indicators.
The relationship between a redox indicator’s change in color and the solution’s electrochemical potential is easily derived by considering the half-reaction for the indicator
Inox + ne- ⇌ Inred
where Inox and Inred are the indicator’s oxidized and reduced forms, respectively. The corresponding Nernst equation for this reaction is
\(\
E=\bf{E}_{\bf{In}_{ox}/\bf{In}_{red}}^0-{0.05916\over n}log{[\bf{In}_{red}]\over [\bf{In}_{ox}]}
\)
If we assume that the indicator’s color in solution changes from that of Inox to that of Inred when the ratio [Inred]/[Inox] changes from 0.1 to 10, then the end point occurs when the solution’s electrochemical potential is within the range
\(\
E=\bf{E}_{\bf{In}_{ox}/\bf{In}_{red}}^0\pm{ 0.05916\over n}
\)
Table below shows some examples of general redox indicators
Table showing Redox Indicators
| Indicator | Colour | Solution | E0 (V) | |
| Reduced form | Oxidized form | |||
| Nitroferroin | Red | Pale Blue | 1 mol/L H2SO4 | 1.25 |
| Ferroin | Red | Pale Blue | 1 mol/L H2SO4 | 1.06 |
| Diphenylamine sulfonic acid | Colourless | Purple | Dilute acid | 0.84 |
| Diphenylamine | Colourless | Violet | 1 mol/L H2SO4 | 0.76 |
| Methylene Blue | Blue | Colourless | 1 mol/L acid | 0.53 |
| Indigo tetrasulfonate | Colourless | Blue | 1 mol/L acid | 0.36 |
A 25.0 mL solution of sodium ethanedioate (Sodium oxalate) ofconcentration 0.10 mol/L was placed in a titration flask. A solution of potas- sium manganate(VII) of concentration 0.038 mol/L was run from a burette intothe titration flask. To ensure that the reaction takes place at a suitable rate, thesolution was heated to nearly 60°c before potassium manganate (VII) solution was run in from burette.
- Write the balanced overall redox reaction given the following half-reac- tions:
Oxidation half-reaction: C2O42- → 2 CO2 + 2e-
Reduction half-reaction: MnO4- (aq) + 8H3O+(aq) + 5e- ⇌ Mn2+ (aq) + 12H2O(l)
- Which indicator is the most suitable to use in this titration?
- Derive the expression for Eeq
- What volume of the manganate(VII) solution would be needed to reachthe end point of the titration?
- Answer


