14.2: Fundamentals of Volumetric Chemical Analysis, Acid/Base Equilibria & Titrations

Learning Objectives

Review the concept of chemical equilibria, and in particular ionic equilibria.

• Define and distinguish between acids and bases.
• Distinguish between monoprotic and polyprotic acid-base equilibrium.
• Describe and distinguish between weak acid/base dissociations.
• Have a working knowledge of the fundamentals of volumetric analysis.
• Define and distinguish between equivalence and end point.
• Use the concept of titration to distinguish between blank and back titrations.
• Define neutralization reactions and explain their corresponding titration curve structures.
• Define and explain standardization, indicators, and primary standards and their use
• Use the concept of polyprotic acid equilibria to do related calculations.

Some of the most important processes in chemical and biological systems are acid-base reactions in aqueous solutions. At the onset of this unit, a review of the topic of acid-base equilibria, together with the properties of acids and bases is undertaken. This is because the concepts of ionic equilibria and reactions are important for a better understanding of the ideas and workings of acid-base neutralization titrations. This unit discusses the basic principles of titrimetric analytical methods, and the use of the equivalence concept in quantitative titration methods. The latter part of this unit will provide you with the opportunity to carry out simple acid-base titration reactions and calculations as well as demonstrations of simulated acid-base titrations.

Key Concepts

• Arrhenius Acid: A substance that yields hydrogen ions (H⁺) when dissolved in water.
• Arrhenius Base: A substance that yields hydroxide ions (OH^-) when dissolved in water.
• Bronsted acid : A substance capable of donationg a proton.Bronsted base: A substance capable of accepting a proton.
• Chemical Equilibrium: A state in which the rates of the forward and reverse reactions are equal.
• Chemical Reaction: A process in which a substance (or substances) is changed into one or more new substances.
• End point: The volume of titrant required for the detection of the equivalence point.
• Equilibrium constant: A number equal to the ratio of the equilibrium concen- trations of products to the equilibrium concentrations of reactants, each raised tothe power of its stoichiometric coefficient.
• Equivalence point: The point at which the acid has completely reacted with or been neutralized by the base.
• Indicators: Substancesthathavedistinctlydifferentcoloursinacidicandbasic media.
• Molar solubility: The number of moles of solute in one litre of a saturated so- lution (mol/L)
• Monoprotic acid: Each unit of the acid yields one hydrogen ion upon ioniza- tion.
• Neutralization reaction: A reaction between an acid and a base.
• Precipitation reaction: A reaction that results in the formation of a precipitate.
• Primary Standard: a high purity compound used to prepare the standard solution or to standardize the solution with.
• Quantitative analysis: The determination of the amount of substances present in a sample.
• Secondary Standard: a second material used as a substitute for a suitable primary standard. This standard solution should always be standardized using a primary standard.
• Solubility product, K_sp: The equilibrium constant for the reaction in which a solid salt dissolves to give its constituent ions in solution. It expresses the equilibrium between a solid and its ions in solution.
• Standardization: The process by which the concentration of a solution is deter- mined.
• Standard Solution: A solution of accurately known concentration.
• Stoichiometry: The quantitative study of reactants and products in a chemical reaction.
• Stoichiometric amounts: The exact molar amounts of reactants and products that appear in the balanced chemical equation.
• Strong acids: Strong electrolytes which are assumed to ionize completely in water.
• Strong bases: Strong electrolytes which are assumed to ionize completely in water.
• Titration: The gradual addition of of a solution of accurately known concentration to another solution of unknown concentration until the chemical reaction between the two solutions is complete.
• Volumetric methods of analysis:based on the measurement of the amount of reagent that combines with the analyte. The terms volumetric analysis specifically involves the determination of the volume of the reagent solution needed for a complete reaction.
• Volumetric titrimetry: methods that require that a reagent solution of known concentration, standard solution or titrant, be used.

Introduction to activity # 2

The thrust of this unit deals primarily with the fundamentals of volumetric methods of analysis. Volumetric method of analysis or sometimes referred to as titrimetric method of analysis is a quantitative method of analysis that is based upon the measurement of volume. These methods are considered important since they are usually rapid, convenient and are often accurate. The concept of pH and the pH scale, the ionization of weak acids and weak bases are introduced and discussed at length. Also, the unit looks at the relationship between acid strength and molecular structure.

List of other compulsory readings

Chemical equilibria (Reading #9)

Introduction to acid-base chemistry (Reading #10)

Acid-Base equilibria and Calculations (Reading #11)

Acid-base equilibria of aquatic environment (Reading #12)

A reference text with file with sub-sections containing sample problemsdealing with acids and bases, chemical equilibrium, quantitative calcula-tions in acids and bases (Reading #13).

Acid Base (Reading #14)

Bronsted-Lowry Acid-Base Reactions (Reading #15)

Chemistry Chapter 16 Complex Ions (Reading #16)

Chemistry Chapter 16 Hydrolysis of Bases (Reading #17)

Chemistry Chapter 16 Titrations (Reading #18)

Chemistry Chapter 16 Hydrolysis of Acids (Reading #19)

Chemistry Chapter 16 Autoionization of Water (Reading #20)

Addition of Strong Base to a weak Acid (Reading #21)

pH curves (titration curves) (Reading #22)

Titration of a Weak Acid with a Strong Base (Reading #23)

Detailed description of the activity

Review of General concepts and Principles of Chemical Equilibria:

The concept of equilibrium is extremely important in chemistry. For example, an industrial chemist who wants to maximize the yield of sulphuric acid, must have a clear understanding of the equilibrium constants for all the steps in the process, starting from the oxidation of sulphur as a reactant and ending with theformation of the final product. For a “general” reaction at equilibrium, we write:

\[\ce{aA + bB <=> cC + dD}\]

where the double arrow, ⇔ , is used to indicate that the chemical reaction proceeds in both directions. Dynamic equilibrium is said to occur when the rate of the forward reaction (represented by the chemical reaction,

\[\ce{aA + bB -> cC + dD}\]

which implies that a moles of substance A reacts with b moles of substance B to form c moles of C and d moles of D) equals the rate of the reverse reaction represented by the chemical reaction

\[\ce{cC + dD -> aA + bB}\]

which again implies that \(c\) moles of substance \(C\) reacts with \(d\) moles of substance \(D\) to form \(a\) moles of \(A\) and \(b\) moles of \(B).

At equilibrium, when there is no net change in any of the concentrations of the materials involved in that reaction over time,

\[\bf{K}_{eq}={[C]^c[D]^d\over \bf{[A]}_{eq}^a\bf{[B]}_{eq}^b}\]

where the K_eq is the equilibrium constant and the square brackets, [ ], indicate a concentration of a species relative to the standard state for that particular phase at equilibrium. The standard state and their standard concentrations are:

[solutes] = mol/L; [gases] = atmospheres (atm) and [pure liquids], [pure solids], and [solivents] = unity.

For most calculations required for this module, it is sufficient to rememberthat the molar concentrations are to be used in the equilibrium expressions.

Types of Equilibria:

There are 4 main types of chemical equilibria that will be discussed in this module:

1. Solubility Equilibria
2. Acid-Base Equilibria
3. Oxidation/Reduction Equilibria and
4. Complex ion Formation Equilibria

In this unit, our discussions will be limited to solubility and acid-base equilibria. The latter two equilibria types will be dealt with in the subsequent two units of this module.

Solubility Equilibria: In solubility equilibrium, (see equation below) a moles of the analyte A reacts with r moles of the reagent, R, to form an insoluble species,A_aR_r. Recall that the standard state for a solid solution is unity (i.e., x = 1). The solid precipitate is assumed to be pure, thus has x =1. Thus, because of this, the concentration of A_aR_r (s) does not appear in the solubility product expression given below.

\[aA(aq) + rR(aq)\Leftrightarrow\bf{A}_a\bf{R}_x(s)$$
\[\bf{K}_{sp}={[A]^a[R]^r}\]

where K_sp is defined as the solubility product constant.

The sequence of steps for (a) calculating K_sp from solubility data and (b) calculating solubility from K_sp data are given in the figure below:

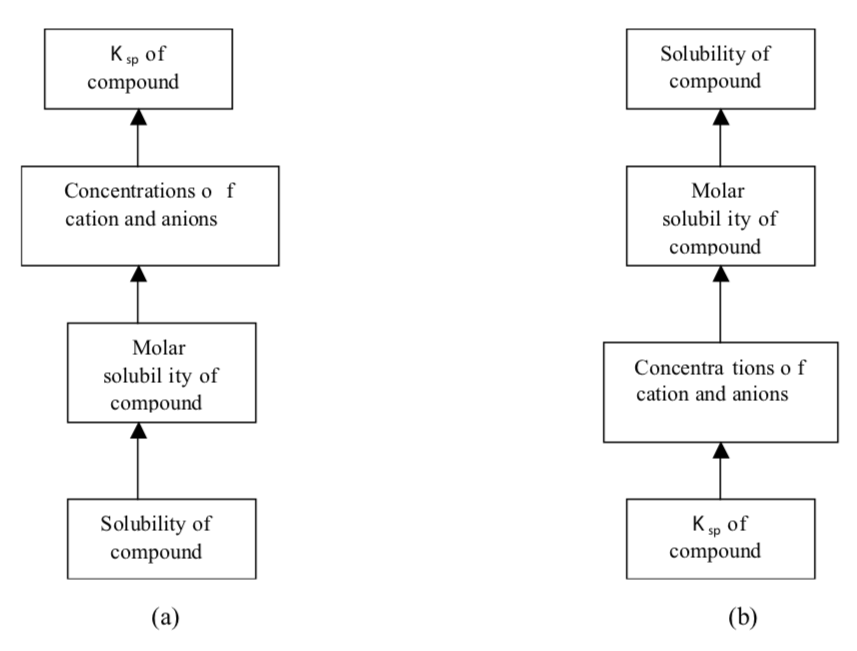
Here, molar solubility, is the number of moles of solute in 1 L of a standard solution (mol/L), and solubility, which is the number of grams of solute in 1 L of a saturated solution (g/L). Note that both of these expressions refer to the concentration of saturated solutions at some given temperature (usually 25^oC).

Example \(\PageIndex{1}\)

Consider the reaction in which a solid salt of mercury chloride dis- solves in water to give its constituent ions in solutions as shown below:

\[\ce{Hg2Cl2 (s) <=> Hg2^{+} (aq) + 2Cl^{−} (aq)}\]

If the solubility product, K is 1.2 x 10^-18, then

Hg₂Cl₂ (s) É Hg₂⁺ (aq) + 2Cl⁻ (aq)

Initail Conc. 0 0

Final Conc. x 2x

where x equals solubility only if there is little ion-pair formation. Therefore,

\[K_{sp} = 1.2 \times 10^{-18} = [Hg2^{2+}] [Cl^{-}]^2\]

This implies that: [Hg_2²⁺] [Cl^-]² = 1.2 x 10^-18. Thus, (x) (2x^-)² = 1.2 x 10^-18

Therefore, the solubility x = 6.7 x 10^-7 M.

Since some dissolved Hg₂Cl₂ may not dissociate into free ion, we say that its solubility is at least 6.7×10^-7 M.

Example \(\PageIndex{2}\): solubility of calcium sulfate

The solubility of calcium sulfate (CaSO₄) is found to be 0.67 g/L. Calculate the value of K_sp for calcium sulfate.

Solution

Please note that we are given the solubility of CaSO₄ and asked to calculate its K_sp. The sequence of conversion steps, according to the Figure above is:

Solubility of → Molar Solubility → [Ca²⁺] → K_sp of

CaSO₄ of CaSO and [SO 2-] CaSO₄

Now consider the dissociation of CaSO₄ in water. Let s be the molar solubility (in mol/L) of CaSO₄.

CaSO₄ (s) ⇌ [Ca²⁺] (aq) + SO₄^2- (aq)​

Initial (M): 0 0

Change (M): -s +s +s

Equilibrium (M): s s

The solubility product of CaSO4 is:

K_sp = [Ca²⁺] [SO₄^2-] = S²

First, we calculate the number of moles of CaSO₄ dissolved in 1 L of solution.

\[
\frac { 0.67 \mathrm { g } ~\mathrm { CaSO } _ { 4 } } { 1 \mathrm { L } \text { solution } } \times \frac { 1 \mathrm { mol }~ \mathrm { CaSO } _ { 4 } } { 136.2 \mathrm { g } ~\mathrm { CaSO } _ { 4 } } = 4.9 \times 10 ^ { - 3 } \mathrm { mol } / \mathrm { L } = \mathrm { s }
\nonumber\]

From the solubility equilibrium we see that for every mole of CaSO₄ that dissolves,

1 mole of Ca²⁺ and 1 mole of SO₄ ^2- are produced. Thus, at equilibrium

[Ca²⁺] = 4.9 x 10^-3 M and [SO₄ ^2-] = 4.9 x 10^-3 M

Now we can calculate K_sp:

K_sp = [Ca²⁺] [SO₄ ^2-]
= (4.9 x 10^-3) (4.9 x 10^-3)
= 2.4 x 10^-5

Exercise \(\PageIndex{1}\)

Exercise 1: The solubility of lead chromate (PbCrO₄) is 4.5 x 10^-5 g/L. Calculate the solubility product of this compound.

Answer

Add texts here. Do not delete this text first.

Acid-Base Equilibria

Theory of Acids and Bases (Arrhenius and Bronsted-Lowry Theories):

According to the Arrhenius Theory of Acids: All acids contain H⁺ ions andAll bases contain OH^- ions; and that an acid-base reaction involves the reaction of hydrogen and hydroxide ions to form water. The corresponding equation is as below:

H⁺ (aq) + OH^- (aq) → H₂O (i)

Where (aq) stands for aqueous phase in which the species exists and l, the liquid phase.

Problems with Arrhenius Theory are two-fold:

(i) Theory requires bases to have an OH^- group. However, we know that ammonia (whose structural formula is NH₃) does not contain the OH^- group but is nonetheless a base.

(ii) Theory does not consider the role of the solvent water, H₂O. These shortcomings are overcome by the Bronsted-Lowry Theory.

Bronsted-Lowry Theories on acids and bases:

Acid: An acid as any substance that can donate a proton to a base.

HA

+

H2O

->

A^-

+

H3O^+

acid base conjugate Conjugate

base of HA acid of H₂O

Base: A base is any substance that can accept a proton from an acid.

NH₃ + H₂O -> NH₄⁺ + OH^-

base acid conjugate acid conjugate base

We now recognize that NH₃ acts as a base (proton acceptor) because of its role as a hydrogen atom acceptor in the reaction and H₂O acts as an acid (proton donor). Moreover, H₂O is now included as a solvent in our consideration. The conjugate acid of NH₃ is NH₄⁺ while the conjugate base of water in the reaction is OH-. NH₄⁺/NH₃ are referred to as conjugate acid/base pair.

In these two examples, water has acted as either an acid or a base, hence a unique solvent. This is one of the Hence it is called water is called an amphiprotic sol- vent. It undergoes self ionization in a process called (autoprotolysis) as shown below:

H₂O + H₂O ↔ H₃O⁺ + OH^-

In the study of acid-base reactions, the hydrogen ion concentration is key; its value indicates the acidity or basicity of the solution. In pure water, only 1 water in 10⁷ undergoes autoprotolysis. This implies that only a very small fraction of water molecules are ionized, hence the concentration of water, [H₂O], remains virtually unchanged. Therefore, the equilibrium constant for the autoionization of water according to the immediate above equation is

K_c = [H₃O⁺][OH^-]

And because we use H⁺ (aq) and H₃O⁺ (aq) interchangeably to represent the hydrated proton, the equilibrium constant can also be expressed as

K_c = [H⁺][OH^-]

To indicate that the equilibrium constant refers to the autoionization of water, we replace K_c by K_w

K_w = [H₃O⁺][OH^-] = [H⁺][OH^-]

Where is the ion-product constant, which is the product of the molar concentra- tions of H⁺ and OH^- ions at a particular temperature.

In pure water at 25^oC, the concentrations of H⁺ and OH^- ions are equal and found to be [H⁺] = 1.0 x 10^-7 M and [OH^-] = 1.0 x 10^-7 M. From the above equation

K_w = (1.0 x 10^-7 M) (1.0 x 10^-7 M) = 1.0 x 10^-14

Note that, whether we have pure water or an aqueous solution of dissolved species, the following relation always holds at 25oC:

K_w = [H⁺][OH^-] = 1.0 x 10^-14

Whenever [H⁺] = [OH^-], the aqueous solution is said to be neutral. In an acidic solution, there is an excess of H+ ions and [H⁺] > [OH^-]. In a basic solution, there is an excess of hydroxide ions, so [H⁺] < [OH^-]. In practice, we can change the concentration of either H⁺ or OH^- ions in solution, but we cannot vary both of them independently. If we adjust the solution so that [H⁺] = 1.0 x 10^-6 M, the OH^- concentration must change to

\[
\left[ \mathrm { OH } ^ { - } \right] = \frac { \mathrm { K } _ { \mathrm { w } } } { \left[ \mathrm { H } ^ { + } \right] } = \frac { 1.0 \times 10 ^ { - 14 } } { 1.0 \times 10 ^ { - 6 } } = 1.0 \times 10 ^ { - 8 } \mathrm { M }
\nonumber\]

Example \(\PageIndex{3}\):

Calculate the concentration of H+ ions in a certain cleaning solution if the concentration of OH- ions is 0.0025 M.

Solution

We are given the concentration of the OH^- ions and asked to calculate [H⁺]. We also know that K_w = [H⁺][OH^-] = 1.0 x 10^-14. Hence, by rearranging the equation,

\[
\left[ \mathrm { H } ^ { + } \right] = \frac { \mathrm { K } _ { w } } { \left[ \mathrm { OH } ^ { - } \right] } = \frac { 1.0 \times 10 ^ { - 14 } } { 0.0025 } = 4.0 \times 10 ^ { - 12 } \mathrm { M }
\nonumber\]

Exercise \(\PageIndex{2}\)

Cacultate the concentration OH^- ions in HCl solution whose hydrogen ion concentration is 1.4 x 10^-3 M.

Answer

pH as a measure of acidity:

The pH of a solution is defined as the negative logarithm of the hydrogen ionconcentration (in mol/L).

\[
\mathrm { pH } = - \log \left[ \mathrm { H } _ { 3 } \mathrm { O } ^ { + } \right] \text { or } \mathrm { pH } = - \log \left[ \mathrm { H } ^ { + } \right]
\]

Note that because pH is simply a way of expressing hydrogen ion concentration, acidic and basic solutions at 25^oC can be distinguished by their pH values, as follows:

Acidic solutions: [H⁺] > 1.0 x 10^-7 M, pH < 7.00

Basic solutions: [H⁺] < 1.0 x 10^-7 M, pH > 7.00

Neutral solutions: [H⁺] = 1.0 x 10^-7 M, pH = 7.00

Note that pH increases as [H⁺] decreases.

Now, taking the negative logarithm of both sides of the expression [H⁺][OH^-] = 1.0 x 10^-14

yields the expression,

-log ([H⁺][OH-]) = -log (1.0 x 10^-14)

-(log ([H⁺]) + log ([OH^-]) = -log (1.0 x 10^-14)

-log ([H⁺]) - log ([OH^-]) = 14.00

From the definitions of pH and pOH we obtainpH + pOH = 14.00

This expression provides us with another way of showing the relationship between the H⁺ ion concentration and the OH^- ion concentration.

Example \(\PageIndex{4}\):

The pH of a rain water sample collected in the Western Province of Kenya on a particular day was found to be 4.82. Calculate the H⁺ ion concentra- tion of the rain water.

Solution:

We know that pH = -log [H⁺] = 4.82

Therefore, log [H⁺] = -4.82

This implies that [H⁺] = antilog (-4.82)

Therefore, [H⁺] = 10^-4.82 = 1.5 x 10^-5 M.

Exercise \(\PageIndex{3}\)

If the pH of a mixture of orange and passion juice is 3.30, calculate the H+ ion concentration.

Answer

Exercise \(\PageIndex{4}\)

Calculate the hydrogen ion concentration in mol/L for solutions with the following pH values: (a) 2.42, (b) 11.21, (c) 6.96, (d) 15.00

Answer

Add texts here. Do not delete this text first.

Base/Acid Ionization Constant:

In the reaction below,

NH₃ + H₂O ⇌ NH₄⁺ + OH^-

base acid conjugate conjugate

acid base

we can write the following equilibrium expression, called the base ionization constant, Kb.

\[
\mathrm { K } _ { \mathrm { b } } = \frac { \left[ \mathrm { NH } _ { 4 } ^ { + } \right] \left[ \mathrm { OH } ^ { - } \right] } { \left[ \mathrm { NH } _ { 3 } \right] } = 1.8 \times 10 ^ { - 5 }
\nonumber\]

Note that water does not explicitly appear in the equilibrium expression because the reaction is taking place in water (water being the solvent). It is important to note that the larger the K_b, the stronger the base. Since NH₃ is a known weak base, there will be a reasonable amount of unreacted NH₃ in solution when equilibrium is established. Hence the low value of its K_b.

Strength of Acids and Bases

Strong acids are assumed to ionize completely in water. Examples of strong acids are hydrochloric acid (HCl), nitric acid (HNO3), perchloric acid (HClO4) and sulphuric acid (H2SO4). Most acids are weak acids, which ionize only to a limited extent in water.

Strong bases ionize completely in water. Examples of strong bases are Hydroxi- des of alkali metals (e.g., NaOH, KOH, etc).

Dissociation of Weak acids and Bases:

Weak Acids:
If HA is a weak acid, then

HA + H₂O ↔ H₃O⁺ + A^-

\[
\mathrm { K } _ { \mathrm { A } } = \frac { \left[ \mathrm { H } _ { 3 } \mathrm { O } ^ { + } \right] \left[ \mathrm { A } ^ { - } \right] } { [ \mathrm { HA } ] }
\]

Weak base:

If B is a weak base, then

B + H₂O ↔ BH⁺ + OH^-

\[
\mathrm { K } _ { \mathrm { B } } = \frac { \left[ \mathrm { OH } ^ { - } \right] \left[ \mathrm { BH } ^ { + } \right] } { [ \mathrm { B } ] }
\]

Note that water is not included in both expressions because it is a constant.

Example \(\PageIndex{5}\):

Determine the pH of a 0.10 M acetic acid solution, if the acid disso- ciation constant, K is 2.24 x 10-5.

We need to know that acetic acid is a weak acid which will only ionize to a limited extent. This can be represented by the equilibrium reaction below:

HAc + H₂O ↔ H₃O⁺ + Ac^-

\[
\mathrm { K } _ { \mathrm { A } } = \frac { \left[ \mathrm { H } _ { 3 } \mathrm { O } ^ { + } \right] \left[ \mathrm { A } ^ { - } \right] } { [ \mathrm { HA } ] }
\nonumber\]

Since both a H₃O⁺ and a A^- is produced for each HA that dissociates:

[H₃O⁺] = [A^-]

Also,

[HA] = 0.10 M –[H₃O⁺]

Suppose y = [H₃O⁺], then

K_A = 2.24 x 10^-5 = y² / (0.10-y)A

Rearranging yields a quadratic equation of the form: y² + 2.24 x 10^-5 y – 2.24 x 10^-6 = 0

Note that this quadratic equation can be solved

using $$
y = \frac { - b \pm \sqrt { \left( b ^ { 2 } - 4 a c \right) } } { 2 a }
\nonumber\]

or the solution can be estimated by assuming that the amount of acid dissociated is insignificant when compared with the undissociated form ( HAc).

Let us try the exact solution using

using $$
y = \frac { - b \pm \sqrt { \left( b ^ { 2 } - 4 a c \right) } } { 2 a }
\nonumber\]

y = [-2.24 x 10^-5 + {(2.24 x 10^-5)² – (4 x 2.24 x 10^-6)}^1/2]/2

y = 0.00149

Therefore, pH = -log (0.00149) = 2.82

Exercise \(\PageIndex{5}\)

The K_a for benzoic acid is 6.5 x 10^-5. Calculate the pH of a 0.10 M benzoic acid solution.

Answer

Exercise \(\PageIndex{6}\)

The pH of an acid solution is 6.20. Calculate the K_a for the acid. The initial acid concentration is 0.010 M.

Answer

Add texts here. Do not delete this text first.

Dissociation of Weak bases:

The calculations are essentially the same as for weak acids. The important ex- pression to remember is:

pH + pOH = pK_w = 14.00

Also, it can be shown that pK_A + pK_B = 14.00, where pK_A = -log (K_A) Note the following:

• If you are starting with an acid, acidic conditions or the conjugate acid of a base, then perform your calculations using K_A.
• If starting with a base, basic conditions or the conjugate base of an acid, then do your calculations using K_B.
• You can readily convert pH to pOH (i.e., pH + pOH = 14.00) and K_A toKB (i.e., pK_A + pK_B = 14.00) values.

Fundamentals of Volumetric Analysis

Volumetric or titrimetric analyses are quantitative analytical techniques which employ a titration in comparing an unknown with a standard. In a titration, a measured and controlled volume of a standardized solution, a solution containing a known concentration of reactant «A» from a buret is added incrementally to a sample solution of known volume (measured by a pipete) containing a substance to be determined (analyte) of unknown concentration of reactant «B». Th titration proceeds until reactant «B» is just consumed (stoichiometric completion). This is known as the equivalence point. (The titration is complete when sufficienttitrant has been added to react with all the analyte.) At this point the number ofequivalents of «A» added to the unknown equals the number of equivalents of «B» originally present in the unknown.

An indicator, a substance that have distinctly different colours in acidic and basic media, is usually added to the reaction flask to signal when and if all the analytehas reacted. The use of indicators enables the end point to be observed. In this, the titrant reacts with a second chemical, the indicator, after completely reacting with the analyte in solution. The indicator undergoes a change that can be detected (like colour). The titrant volume required for the detection of the equivalence point is called the end point. Note that the end point and equivalence point are seldomly the same. Ideally, we want the equivalence point and the end point to be the same. This seldom happens due to the methods used to observe end points. As a result, we get a titration error, the difference between the end point and the equivalence point, which leads to overtitration.

The end point is then the point where sufficient indicator has been converted fordetection. The sequence of events can be demonstrated as below:

followed by

The last step does NOT require that all indicator be converted. Infact, it is best if a very small percent need to be reacted to make the colour change visible.

For volumetric methods of analysis to be useful, the reaction must reach 99%+ completion in a short period of time. In almost all cases, a burette is used to measure out the titrant. When a titrant reacts directly with an analyte (or with a reaction the product of the analyte and some intermediate compound), the procedure is termed a direct titration. The alternative technique is called a back titration. Here, an intermediate reactant is added in excess of that required to exhaust the analyte, then the exact degree of excess is determined by subsequent titration of the unreacted intermediate with the titrant. Regardless of the type of titration, an indicator is always used to detect the equivalence point. Most com- mon are the internal indicators, compounds added to the reacting solutions that undergo an abrupt change in a physical property (usually absorbance or color) at or near the equivalence point. Sometimes the analyte or titrant will serve this function (auto indicating). External indicators, electrochemical devices such as pH meters, may also be used. Ideally, titrations should be stopped precisely at the equivalence point. However, the ever-present random and systematic error, often results in a titration endpoint, the point at which a titration is stopped, that is not quite the same as the equivalence point. Fortunately, the systematic error, or bias may be estimated by conducting a blank titration. In many cases the titrantis not available in a stable form of well-defined composition. If this is true, thetitrant must be standardized (usually by volumetric analysis) against a compound that is available in a stable, highly pure form (i.e., a primary standard).

Note that by accurately measuring the volume of the titrant that is added (using a buret), the amount of the sample can be determined.

For a successful titrimetric analysis, the following need to be true:

• The titrant should either be a standard or should be standardized.
• The reaction should proceed to a stable and well defined equivalence point.
• The equivalence point must be able to be detected.
• The titrant’s and sample’s volume or mass must be accurately known.
• The reaction must proceed by a definite chemistry. There should be nocomplicating side reactions.
• The reaction should be nearly complete at the equivalence point. In other words, chemical equilibrium should favour the formation of products.
• The reaction rate should be fast enough to be practical.

Illustration: In the determination of chloride, 50 ml of a 0.1M AgNO₃ solution would be required to completely react with 0.005 moles of chloride present in solution.

Balanced Equation for the reaction: Ag⁺(aq) + Cl^-(aq) → AgCl(s). Here, 1 mole of Ag⁺ ions reacts stoichiometrically with 1 mole of Cl^- ions. Therefore 50 ml (0.05L) of a standard 0.10M AgNO₃ which contains 0.005 moles (= 0.10 moles L-1 x 0.050 L) requires an equivalent number of moles of Cl^- ions.

Since the titrant solution must be of known composition and concentration, we ideally would like to start with a primary standard material, a high purity compound used to prepare the standard solution or to standardize the solution with. A standard solution is one whose concentration is known. The concentration of a standard solution is usually expressed in molarity (mole/liter). The process by which the concentration of a solution is determined is called standardization. Because of the availability of some substances known as primary standards, in many instances the standardization of a solution is not necessary. Primary standard solutions are analytically pure, and by dissolving a known amount of aprimary standard in a suitable medium and diluting to a definite volume, a solutionof known concentration is readily prepared. Most standard solutions, however, are prepared from materials that are not analytically pure and they have to be standardized against a suitable primary standard.

The following are the desired requirements of a primary standard:

• High purity
• Stable in air and solution: composition should be unaltered in the air at ordinary or moderately hgh temperatures.
• Not hygroscopic.
• Inexpensive
• Large formula weight: equivalence weight ought to be high in order to reduce the effects of small weighing error.
• Readily soluble in the solvent under the given conditions of the analy- sis.
• On titration, no interfering product(s) should be present.
• The primary standard should be colorless before and after titration to avoid interference with indicators.
• Reacts rapidly and stoichiometrically with the analyte.

The following are also the desired requirements of a primary standard solution:

• Have long term stability in solvent.
• React rapidly with the analyte.
• React completely with analyte.
• Be selective to the analyte.

The most commonly used primary standards are:

A. Acidimetric standards.

Sodium carbonate (Na₂Co₃, equivalent weight 53.00) and Borax (Na₂B₄O₇.10H₂O, equivalent weight 63.02)

B. Alkalimetric standards.

Sulphamic acid (NH₂ SO₃H, equivalent weight 97.098),

Potassium hydrogenphthalate (KHC₈H₂O₄, equivalent weight 204.22)

Oxalic acid (H₂C₂O₄.2H₂O, Equivalent weight 63.02)

This is a second material used As a substitute for a suitable primary standard, asecondary standard are often used as a second material. However, the standard solution should always be standardized using a primary standard.

Exercise \(\PageIndex{7}\)

Discuss the following analytical terms: Standard solution; Primary standards; Standardized solution; Standardization; End point of titration; Equi- valence point of titration; and Titration error

Answer

Summary:

The basic requirements or components of a volumetric method are:

1. A standard solution (i.e., titrant) of known concentration which reacts with the analyte in a known and repeatable stoichiometry (i.e., acid/base, precipitation, redox, complexation).
2. A device to measure the mass or volume of sample (e.g., pipet, graduatedcylinder, volumetric flask, analytical balance).
3. A device to measure the volume of the titrant added (i.e., buret).
4. If the titrant-analyte reaction is not sufficiently specific, a pretreatment toremove interferents.
5. A means by which the endpoint can be determined. This may be an in- ternal indicator (e.g., phenolphthalein) or an external indicator (e.g., pH meter).

Apparatus for titrimetric analysis:

The most common apparatus used in volumetric determinations are the pipette,buret, measuring cylinder, volumetric and conical (titration) flask. Reliablemeasurements of volume is often done with the help of a pipet, buret, and a vo-lumetric flask. The conical flask is preferred for titration because it has a good“mouth” that minimizes the loss of the titrant during titration.

Classification of reactions in volumetric (titrimetric) analysis

Any type of chemical reactions in solution should theoretically be used for ti- trimetric analysis. However, the reactions most often used fall under two main categories:

(a) Those in which no change in oxidation state occurs. These are dependent on combination of ions.

(b) Oxidation-reduction reactions: These involve a change of oxidation state (i.e., the transfer of electrons).

For convenience, however, these two types of reactions are further divided into four main classes:

(i) Neutralization reactions or acidimetry and alkalimetry: HA+B⇌HB+ +A-

(ii) Precipitation reactions: M(aq) +nL(aq) ⇌ ML_n(s)

(iii) Oxidation-reduction reactions: Ox + Red ⇌ Red' + ox'

(iv) Complex ion formation reactions: M(aq) +nL(aq) ⇌ ML_n(aq)

In this unit, we shall focus on neutralization reactions. The latter two will be dealt with in the next two units that follow in this module.

General Theory of Titrations

In determining what happens during a titration process, some of the theories of chemical equilibria (previously covered in this unit as well as in an earlier Module entitled General Chemistry) are often used. To fully understand what happens during a titration experiment enables one to set up a titration and choose an indicator wisely.

Consider a hypothetical titration reaction illustrated as follows:

T+A→P_x +P_y
where T is the titrant (considered as the standard), A is the titrand (considered as the

unknown analyte whose concentration is desired), and P_x and P_y are products. Note that the extent of the above hypothetical reaction is determined by the magnitude of the equilibrium constant,

\[
\mathrm { K } _ { \mathrm { eq } } = \frac { \left[ \mathrm { P } _ { x } \right] \left[ \mathrm { P } _ { y } \right] } { [ \mathrm { T } ] [ \mathrm { A } ] }
\]

Suppose C_t is the concentration of the titrant which must be known (in the buret) and C_A is the concentration of the unknown analyte A in the titration flask before any titrant is added. For the purposes of our illustrations here, we shall assume that both C_t and C_A are known.

In order to understand what is occuring in a titration flask, we shall consider asingle step titration to comprise of four (4) distinct regions described as below:

• Region 1 –Initial Stage (i.e., before the addition of any titrant):
  Here, a pure solution of analyte, A is placed in a titration flask before any volume of reagent is added. At this point there is no titrant, T introduced in the flask, no products P_x or P_y formed yet and [A] in the titration flask is a function of C_A.
• Region 2 –Before equivalence point (i.e., after addition of the titrant but before the equivalence point): Here, the volume of reagent added to analyte is not sufficient to make the reaction complete (when there is excess of analyte). Thus, in this region T becomes the limiting reagent,and hence there will be very little T in solution (in fact [T] in the flask could be zero if the reaction went totally to completion). Therefore, only A, Px and Py would be present in measurable quantities.
• Region 3 –At equivalence point: In this region, the reagent added is the amount that is chemically equivalent to the amount of substance being determined (analyte). The equivalence point is defined as the point at which there would be neither T nor A present if the reaction went to completion. In reality though, there is often very little of either T or A present and there exists a very simple relationship between [T] and [A]. As is expected, only Px and Py would be present in measurable amounts.
• Region 4 –After equivalence point: Here, the amount of reagent added is higher than the amount of substance being determined. In this region, A now becomes the limiting reagent, and therefore there will be very little A (if any, depending on whether the reaction went totally to completion, in which case [A] = 0) in solution. Only T, P_x, and P_y are present in measurable amounts in the titration flask.

In view of the aforementioned, it is clear that the method for determining what is trully present in a titration flask during a titration depends on the region under consideration. To demonstrate what happens and how the concentrations of all substances present varies during a titration process, acid/base titrations will be used as examples of titrations in general. The types of acid/base titrations that will be considered in this unit are:

A) Titration of strong acid with strong base

B) Titration of weak acid with strong base

C) Titration of weak base with strong acid

D) Titration of polyprotic weak acids with strong base

Note that the behaviour in each of the stages mentioned above is a function of the type of acid-base titration process. This behaviour is best depicted or described by making plots of pH as a function of the volume of base added. This plot is known as a titration curve.

Let us now examine each of the types of acid/base titrations mentioned above.

Titration of a Strong acid with a Strong Base

The reaction between HCl (considered here as the unknown) and NaOH (the titrant) will be used as an example. As discussed earlier, strong acids are 100% dissociated in water (i.e., H⁺Cl⁻ +H₂O→H₃O⁺ +Cl^-) and strong bases are 100%hydrolysed (i.e., Na⁺OH⁻ +H₂O→H₂O+OH^- +Na⁺ ).​​​​​​ The reaction therefore between HCl and NaOH can be expressed as:

H₃O⁺ +OH^- →2H₂O

Here, Na⁺ and Cl^- are spectator ions and do not enter into the titration reaction. In this reaction, Cl^- is neither added to the flask nor is it consumed in the reaction in the course of the titration process. Thus the number of moles of Cl^- remains constant while its concentration decreases due dilution. (Remember that the volume of solution in the flask is increasing as titration progresses and this dilution process has an effect on the concentrations.)

If C_t is the concentration of the titrant in the buret and whose value is a fixed; C_A is the concentration of the unknown analyte, A in the flask before the titration and is also a fixed value; V_t is the volume of the titrant added to the titration flask;and V_A is the volume of the unknown analyte placed initially in the titration flask,then the concentration of Cl^-, [Cl^-] which does not depend on the region of the titration is given by

\[
\left[ \left. C \right| ^ { - } \right] = \frac { \text { mol } } { \text { Volume } } = \frac { C _ { A } V _ { A } } { \left( V _ { A } + V _ { t } \right) } \text { and } p C l = - \log [ C l ]
\nonumber\]

Na⁺ is continuously being added to the titration flask in the course of the titration process but is not reacting. Hence, the concentration of Na⁺, [Na⁺] will continuously increase and its concentration will not depend on the region of the titration and is given as

\[
\left[ \mathrm { Na } ^ { + } \right] = \frac { \mathrm { mol } } { \text { Volume } } = \frac {\mathrm{C}_{t} \mathrm { V } _ { \mathrm { t } } } { \left( \mathrm { V } _ { \mathrm { A } } + \mathrm { V } _ { \mathrm { t } } \right) } \text { and pNa } = - \log \left[ \mathrm { Na } ^ { + } \right]
\nonumber\]

Since the species H₃O⁺ and OH^- are involved in the titration reaction, the calculations of [H₃O⁺] and [OH^-] in the titration flask will now depend on the titration region. This is now examined below.

Suppose C_a is the concentration of the strong acid that is present in the flask at any point during the titration process, and C_b is the concentration of the strong base actually present in the titration flask at any point in the titration. Note that these values will always be different from C_t and C_A.

Let us now examine what happens to the concentrations of [H₃O⁺] and [OH^-] in each of the titration regions discussed above.

Region 1: This is simple a solution of the strong acid present in the titration flask.

\[
\left[ \mathrm { H } _ { 3 } \mathrm { O } ^ { + } \right] = \mathbf { C } _ { \mathrm { a } } = \mathbf { C } _ { \mathrm { A } } \text { and } \mathrm { pH } = - \log \left[ \mathrm { H } _ { 3 } \mathrm { O } ^ { + } \right] \text { and } \mathrm { pOH } = 14.00 - \mathrm { pH }
\]

Region 2: As titrant (strong base) is added, some of the strong acid get consu- med, but no strong base is yet present. Thus, only the strong acid affects theoverall pH of the solution in the titration flask.

\[\ Moles of acid remaining = (moles of original acid – moles of base added)\]

\[\bf{C}_a={(moles\ of\ acid\ remaining)\over(total\ resultant\ volume)}={(\bf{V}_a\bf{C}_a-\bf{V}_t\bf{C}_t)\over(\bf{V}_a+\bf{V}_t)}\]

\[[H^+]=\bf{C}_a={(\bf{V}_a\bf{C}_A-\bf{V}_t\bf{C}_t)\over(\bf{V}_a+{V}_t)}\ if\ \bf{C}_a>>2\bf{K}_w^{1/2}\]

Region 3: In this region, there is neither strong acid nor strong base present inthe titration flask. The solution simply contains the salt, NaCl, the product of theacid-base reaction. Since neither Na+ nor Cl- affect pH of the solution mixture, the pH will be that of pure water.

\[
[ \mathrm { H } + ] = \left( K _ { W } \right) ^ { 1 / 2 } \text { or } \mathrm { pH } = 7.00
\]

Region 4: In this region, all the strong acid is now exhausted and there is excess strong base present. Therefore, the pH of the soultion mixture is determined by the excess strong base present.

Moles of base present = (total moles of base added so far – moles of original acidpresent in flask at beginning of titration)

\[Moles\ of\ base\ present={(total\ moles\ of\ base\ added\ so\ far\ -\ moles\ of\ original\ acid\ present\ in\ flask\ at\ beginning\ of\ titration)}\]

\[\bf{C}_a={(moles\ of\ base\ present)\over(total\ resultant\ volume)}={(\bf{V}_t\bf{C}_t-\bf{V}_A\bf{C}_A)\over(\bf{V}_a+\bf{V}_t)}\]

\[[OH^-]=\bf{C}_b={(\bf{V}_t\bf{C}_t-\bf{V}_a\bf{C}_A)\over(\bf{V}_a+{V}_t)}\ if\ \bf{C}_a>>2\bf{K}_w^{1/2}\]

\[[\bf{H}_3O^+]={\bf{K}_w\over[OH^-]}\]

Example \(\PageIndex{6}\):

Consider titration of 100.0 mL of 0.100 mol/L HCl solution with 0.100 mol/L standard NaOH solution.

Region 1: Before addition of any titrant. The 100.0 mL solution contains a strong HCl acid and the total volume is 100 mL (0.100 L).

[Na⁺] = 0.0 mol/L

\[
[ \mathrm { Cl } ^-] = \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol }/ \mathrm { L } ) } { ( 0.100 \mathrm { L } ) } = 0.100 \mathrm { mol } / \mathrm { L }
\nonumber\]

\[
\left[ \mathrm { H } ^ { + } \right] = \mathbf { C } _ { \mathrm { a } } = \mathbf { C } _ { \mathrm { A } } = \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.100 \mathrm { L } ) } = 0.100 \mathrm { mol } / \mathrm { L }
\nonumber\]

\[
[ \mathrm { OH } ^-] = \frac { 1.00 \times 10 ^ { - 14 } } { ( 0.100 ) } = 1.00 \times 10 ^ { - 13 } \mathrm { mol } / \mathrm { L }
\nonumber\]

Region 2: After addition of, say 50.00 mL of NaOH. The solution still contains a strong acid and the total volume is 150.0 mL.

\[
\left[ \mathrm { Na } ^ { + } \right] = \frac { ( 0.0500 \mathrm { L } ) ( 0.100 \mathrm { mol } /\mathrm { L } ) } { ( 0.1500 \mathrm { L } ) } = 0.0333 \mathrm { mol } / \mathrm { L }
\nonumber\]

\[
[ \mathrm { Cl }^- ] = \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol/L } ) } { ( 0.1500 \mathrm { L } ) } = 0.0667 \mathrm { mol } / \mathrm { L }
\nonumber\]

\[
{ \left[ \mathrm { H } ^ { + } \right] = \mathbf { C } _ { \mathrm { a } } = } { \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) - ( 0.0500 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.1500 \mathrm { L } ) } = 0.0333 \mathrm { mol } / \mathrm { L } }
\nonumber\]

\[[ \mathrm { OH ^-} ] = \frac { 1.00 \times 10 ^ { - 14 } } { ( 0.0333 ) } = 3.00 \times 10 ^ { - 13 } \mathrm { mol } / \mathrm { L }\nonumber\]

Region 3: After addition of, say 99.00 mL of NaOH. The solution contains very little of the strong acid and the total volume is 199.0 mL.

\[
\left[ \mathrm { Na } ^ { + } \right] = \frac { ( 0.0990 \mathrm { L } ) ( 0.100 \mathrm { mol/ } \mathrm { L } ) } { ( 0.1990 \mathrm { L } ) } = 0.0498 \mathrm { mol } / \mathrm { L }
\nonumber\]

\[
[ \mathrm { Cl^- } ] = \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.1990 \mathrm { L } ) } = 0.0502 \mathrm { mol } / \mathrm { L }
\nonumber$$
$$
{ \left[ \mathrm { H } ^ { + } \right] = \mathbf { C } _ { \mathrm { a } } = } { \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) - ( 0.0990 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.1990 \mathrm { L } ) } = 5.03 \times 10 ^ { - 4 } \mathrm { mol } / \mathrm { L } }
\nonumber\]

\[
[ \mathrm { OH^- } ] = \frac { 1.00 \times 10 ^ { - 14 } } { \left( 5.03 \times 10 ^ { - 4 } \right) } = 1.99 \times 10 ^ { - 11 } \mathrm { mol } / \mathrm { L }
\nonumber\]

Region 3 Continued: After addition of, say 99.90 mL of NaOH. The solution contains further reduced strong acid and the total volume is 199.90 mL.

\[
\left[ \mathrm { Na } ^ { + } \right] = \frac { ( 0.0999 \mathrm { L } ) ( 0.100 \mathrm { mol/L } ) } { ( 0.199 \mathrm { L } ) } = 0.04998 \mathrm { mol } / \mathrm { L }
\nonumber\]

\[
[ \mathrm { Cl ^-} ] = \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.1999 \mathrm { L } ) } = 0.05003 \mathrm { mol } / \mathrm { L }
\nonumber\]

\[
{ \left[ \mathrm { H } ^ { + } \right] = \mathbf { C } _ { \mathrm { a } } = } { \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) - ( 0.0999 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.1999 \mathrm { L } ) } = 5.00 \times 10 ^ { - 5 } \mathrm { mol } / \mathrm { L } }
\nonumber\]

\[
[ \mathrm { OH^- } ] = \frac { 1.00 \times 10 ^ { - 14 } } { \left( 5.00 \times 10 ^ { - 5 } \right) } = 1.999 \times 10 ^ { - 10 } \mathrm { mol } / \mathrm { L }
\nonumber\]

Region 3 Continued: After addition of, say 99.99 mL of NaOH. The solution contains even further reduced strong acid and the total volume is 199.90 mL.

\[
\left[ \mathrm { Na } ^ { + } \right] = \frac { ( 0.09999 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.19999 \mathrm { L } ) } = 0.049998 \mathrm { mol } / \mathrm { L }
\nonumber\]

\[
[ \mathrm { Cl^- } ] = \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol/ } \mathrm { L } ) } { ( 0.1999 \mathrm { L } ) } = 0.050003 \mathrm { mol } / \mathrm { L }
\nonumber\]

\[
{ \left[ \mathrm { H } ^ { + } \right] = \mathbf { C } _ { \mathrm { a } } = } { \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol/ } \mathrm { L } ) - ( 0.09999 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.1999 \mathrm { L } ) } = 5.00 \times 10 ^ { - 6 } \mathrm { mol/ } \mathrm { L } }
\nonumber\]

\[
[ \mathrm { OH^- } ] = \frac { 1.00 \times 10 ^ { - 14 } } { \left( 5.00 \times 10 ^ { - 6 } \right) } = 2.00 \times 10 ^ { - 9 } \mathrm { mol } / \mathrm { L }
\nonumber\]

Region 3 Continued: After addition of 100.00 mL of NaOH. The solution contains neither a strong acid nor a strong base and the total volume is 200.00 mL

\[
{ \left[ \mathrm { Na } ^ { + } \right] = \left[ \mathrm { Cl } ^ { - } \right] = \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.200 \mathrm { L } ) } = 0.0500 \mathrm { mol } / \mathrm { L } } \\ { \left[ \mathrm { H } ^ { + } \right] = \left[ \mathrm { OH } ^ { - } \right] = 1.00 \mathrm { x } 10 ^ { - 7 } \mathrm { mol } / \mathrm { L } }
\nonumber\]

Region 4: After addition of, say 100.01 mL of NaOH. The solution contains a little strong base and the total volume is 200.01 mL.

\[
\left[ \mathrm { Na } ^ { + } \right] = \frac { ( 0.10001 \mathrm { L } ) ( 0.100 \mathrm { mol/L } ) } { ( 0.20001 \mathrm { L } ) } = 0.050022 \mathrm { mol } / \mathrm { L }
\nonumber\]

\[
[ \mathrm { Cl ^-} ] = \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol/L } ) } { ( 0.20001 \mathrm { L } ) } = 0.0499975 \mathrm { mol/L }
\nonumber\]

\[
{ [ \mathrm { OH^- } ] = \mathbf { C } _ { \mathrm { b } } = } { \frac { ( 0.10001 \mathrm { L } ) ( 0.100 \mathrm { mol/L } ) - ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol/L } ) } { ( 0.20001 \mathrm { L } ) } = 4.99975 \times 10 ^ { 6 } \mathrm { mol } / \mathrm { L } }
\nonumber\]

\[
\left[ \mathrm { H } ^ {+} \right] = \frac { 1.00 \times 10 ^ { - 14 } } { \left( 4.99975 \times 10 ^ { - 6 } \right) } = 2.00 \times 10 ^ { - 9 } \mathrm { mol } / \mathrm { L }
\nonumber\]

Region 4 Continued: After addition of 100.10 mL of NaOH. The solution contains a little strong base and the total volume is 200.10 mL.

\[
\left[ \mathrm { Na } ^ { + } \right] = \frac { ( 0.1001 \mathrm { L } ) ( 0.100 \mathrm { mol/ } \mathrm { L } ) } { ( 0.2001 \mathrm { L } ) } = 0.050025 \mathrm { mol } / \mathrm { L }
\nonumber\]

\[
[ \mathrm { Cl^- } ] = \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol/L } ) } { ( 0.2001 \mathrm { L } ) } = 0.049975 \mathrm { mol } / \mathrm { L }
\nonumber\]

\[
{ [ \mathrm { OH^- } ] = \mathrm { C } _ { \mathrm { b } } = } { \frac { ( 0.1001 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) - ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.2001 \mathrm { L } ) } = 4.9975 \times 10 ^ { 5 } \mathrm { mol } / \mathrm { L } }
\nonumber\]

\[
\left[ \mathrm { H } ^ { + } \right] = \frac { 1.00 \times 10 ^ { - 14 } } { \left( 4.9975 \times 10 ^ { - 5 } \right) } = 2.001 \times 10 ^ { - 10 } \mathrm { mol } / \mathrm { L }
\nonumber\]

Region 4 Continued: After addition of 110.00 mL of NaOH. The solution contains more strong base and the total volume is 210.00 mL.

\[
\left[ \mathrm { Na } ^ { + } \right] = \frac { ( 0.110 \mathrm { L } ) ( 0.100 \mathrm { mol/ } \mathrm { L } ) } { ( 0.210 \mathrm { L } ) } = 0.05238 \mathrm { mol/L }
\nonumber\]

\[
[ \mathrm { Cl^- } ] = \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol/ } \mathrm { L } ) } { ( 0.210 \mathrm { L } ) } = 0.04762 \mathrm { mol } / \mathrm { L }
\nonumber\]

\[
{ [ \mathrm { OH^- } ] = \mathbf { C } _ { \mathrm { b } } = } { \frac { ( 0.110 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) - ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.210 \mathrm { L } ) } = 4.762 \times 10 ^ { - 3 } \mathrm { mol } / \mathrm { L } }
\nonumber\]

\[
\left[ \mathrm { H } ^ { + } \right] = \frac { 1.00 \times 10 ^ { - 14 } } { \left( 4.762 \times 10 ^ { - 3 } \right) } = 2.1 \times 10 ^ { - 12 } \mathrm { mol } / \mathrm { L }
\nonumber\]

Region 4 Continued: After addition of 150.00 mL of NaOH. The solution contains more strong base and the total volume is 250.00 mL.

\[
\left[ \mathrm { Na } ^ { + } \right] = \frac { ( 0.150 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.250 \mathrm { L } ) } = 0.06 \mathrm { mol } / \mathrm { L }
\nonumber\]

\[
[ \mathrm { Cl^- } ] = \frac { ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.250 \mathrm { L } ) } = 0.04 \mathrm { mol } / \mathrm { L }
\nonumber\]

\[
{ [ \mathrm { OH^- } ] = \mathrm { C } _ { \mathrm { b } } = } { \frac { ( 0.150 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) - ( 0.100 \mathrm { L } ) ( 0.100 \mathrm { mol } / \mathrm { L } ) } { ( 0.250 \mathrm { L } ) } = 0.02 \mathrm { mol } / \mathrm { L } }
\nonumber\]

\[
\left[ \mathrm { H } ^ { + } \right] = \frac { 1.00 \times 10 ^ { - 14 } } { ( 0.02 ) } = 5.0 \times 10 ^ { - 13 } \mathrm { mol } / \mathrm { L }
\nonumber\]

The result of a series of such calculations can now be ploted as a graph of pH versus volume of NaOH to generate what is referred to as a titration curve. In such a plot, it becomes evident that the concentrations of the reactants, but not the products or the spectator ions, go through a large change exactly at the equivalence point. It is this change that allows one to pinpoint the equivalence point. The equivalence point can therefore be determined, say in this case, by monitoring either the concentration of OH^- or H⁺ ions.

A typical titration curve for a strong acid versus a strong base is given in the figurebelow. (We’ll take hydrochloric acid and sodium hydroxide as typical of a strongacid and a strong base; i.e., NaOH _(aq) + HCl _(aq) → NaCl _(aq) + H2O _(l) ).

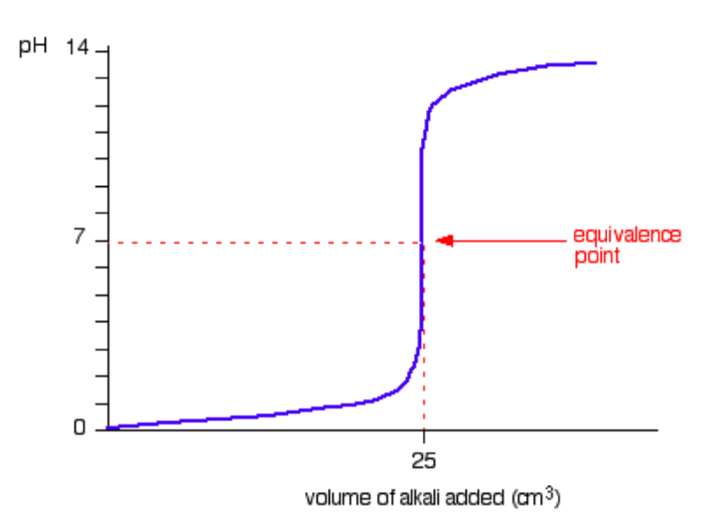
It is clear from this figure that the pH only rises a very small amount until quitenear the equivalence point. Then there is a really steep rise.

In order for you to appreciate the generation of a titration curve from such calcu- lations as above, you are encouraged to do the exercise problem below.

Exercise: Using the above calculations, plot the corresponding titration curve for the titration of 100.00 mL of 0.10 mol/L HCL solution with 0.10 mol/L standard NaOH solution.

Let us now consider the case of titration of a weak acid with a strong base and see how it compares with that of a strong acid with a strong base dealt with above.

Titration of a Weak acid with a Strong Base

At first glance, it might seem that weak acid/strong base titrations are just like the strong acid/strong base titration encountered in the preceding section. However, there is a significant difference that makes this case more complicated. Whereas the product of the titration reaction and the spectator ions in a strong acid/strong base titration (such as H₂O, Na⁺, and Cl^-) do not affect the pH of the solution in the titration flask and can thus be neglected, the same cannot be said of the weak acid/strong base titration. In fact, when a weak acid is titrated with a strong base, one of the products is a weak base which does affect the pH in all the regions discussed above except Region 1, and this must be taken into consideration.

The titration reaction involving a weak acid (HA) with a strong base such as NaOH is often expressed as:

\[
\mathrm { HA } + \mathrm { NaOH } \rightarrow \mathrm { NaA } + \mathrm { H } _ { 2 } \mathrm { O }
\nonumber\]

which can be more accurately represented as:

\[
\mathrm { HA } + \mathrm { OH } ^ { - } \rightarrow \mathrm { A } ^ { - } + \mathrm { H } _ { 2 } \mathrm { O }
\]

with a corresponding equilibrium constant expressed as:

\[
\mathrm { K } _ { \mathrm { eq } } = \frac { \left[ \mathrm { A } ^ { - } \right] } { [ \mathrm { HA } ] \left[ \mathrm { OH } ^ { - } \right] } = \frac { 1 } { \mathrm { K } _ { \mathrm { b } } } = \frac { \mathrm { K } _ { a } } { \mathrm { K } _ { \mathrm { w } } }
\]

Note that K_eq for the titration of a weak acid with an K_a of about 1.0 x 10^-5 will be only 1.0x10⁹ (i.e., \(\ k_{eq}=\)\(\dfrac{1}{K_b}\)=\(\dfrac{K_a}{K_w}\)=\(\dfrac{K_a}{10^{-14}}\)) a value that is not as large as that for a strong acid. However, this is still considered large enough for the reaction to proceed to completion. In fact, as the value of K_a of the weak acid decreases, so does the value of K_eq for the titration. Therefore, if the acid is too weak, it cannot be easily titrated.

A typical titration curve for a weak acid versus a strong base is given in the figurebelow. (We’ll take ethanoic acid and sodium hydroxide as typical of a waek acidand a strong base; i.e., CH3COOH _(aq) + NaOH _(aq) → CH3COONa _(aq) + H2O _(l)).

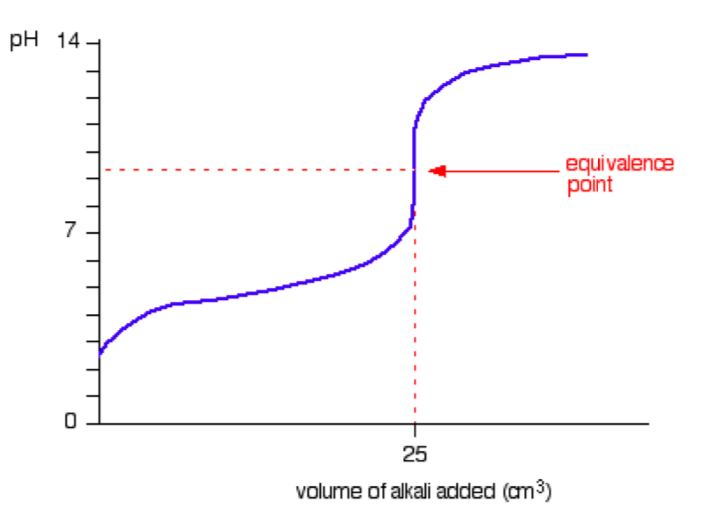
The start of the graph shows a relatively rapid rise in pH but this slows down as a buffer solution containing ethanoic acid and sodium ethanoate is produced. Beyond the equivalence point (when the sodium hydroxide is in excess) the curve is just the same as that end of the HCl-NaOH graph shown previously.

Let us now consider the four regions of the titration in the same manner as for the strong acid/strong base titration. Here again, we shall assume that the weak acid of concentration C_A is the unknown and that the titrant of concentration C_t, is a strong base.

Region 1: Prior to addition of any base, the solution in the titration flask basicallycontains only the weak acid, HA and that C_a = C_A . In order to calculate [H+], a weak acid equation need to be used. Thus

\[
\left[ \mathrm { H } ^ { + } \right] = \left( \mathrm { K } _ { \mathrm { a } } \mathrm { C } _ { \mathrm { A } } \right) ^ { \frac { 1 } { 2 } } , \mathrm { i.e. } , \mathrm { pH } = - \log \sqrt { \mathrm { K } _ { \mathrm { a } } \mathrm { C } _ { \mathrm { A } } }
\]

Region 2: Upon addition of some titrant, the solution contains some unreacted acid, HA (since the acid is not 100% dissociated) and some conjugate base, A-, due to the titration reaction.

Therefore, moles of acid remaining = original moles of acid-moles of strong base added.

\[\bf{C}_a={(moles\ of\ acid\ remaining)\over Total volme}={\bf{V}_A\bf{C}_A-\bf{V}_t\bf{C}_t\over(\bf{V}_A+\bf{V}_t)}\]

Moles of weak base formed = moles of strong base added.

Therefore C_B=V_tC_t\(V_A+V_t), where C_B is concentration of the weak base formed.

To calculate the [H⁺], we need to use the simplified equation for a mixture of a weak acid and its conjugate base, i.e.,

\[
\left[ \mathrm { H } ^ { + } \right] = \frac { \mathrm { K } _ { a } \mathrm { C } _ { \mathrm { a } } } { \mathrm { C } _ { \mathrm { B } } } , \text { i.e., } \mathrm { pH } = \mathrm { pK } _ { \mathrm { a } } + \log \frac { \mathrm { C } _ { \mathrm { B } } } { \mathrm { C } _ { \mathrm { a } } }
\]

Region 3: At the equivalence point, all the weak acid has been completely neu- tralized by the strong base and only the weak base remains. There is no excess strong base present. Since the solution contains a weak base, the pH of the solutionin the flask cannot be equal to 7.00 and must be greater than 7.00.

Moles of weak base present = moles of strong base added.

\[
C _ { B } = \frac { V _ { t } C _ { t } } { \left( V _ { A } + V _ { t } \right) }
\]

[OH^-] can be calculated using the simplified weak base equation, i.e.,

\[
\left[ \mathrm { OH } ^ { - } \right] = \left( \mathrm { K } _ { \mathrm { b } } \mathrm { C } _ { \mathrm { B } } \right) ^ { \frac { 1 } { 2 } }
\]

Region 4: After the equivalence point , both the weak base, A-, and excess strong base, OH-, will be present.

moles of weak base = moles of original weak acid

Concentration of weak base,

\[
\mathbf { C } _ { w } = \frac { V _ { A } C _ { A } } { \left( V _ { A } + V _ { t } \right) }
\]

Moles of strong base present = moles of titrant added – moles of original weak acid

Thus, concentration of strong base,

\[
\mathbf { C } _ { \mathrm { s } } = \frac { \left( \mathrm { V } _ { \mathrm { t } } \mathrm { C } _ { \mathrm { t } } - \mathrm { V } _ { \mathrm { A } } \mathrm { C } _ { \mathrm { A } } \right) } { \left( \mathrm { V } _ { \mathrm { A } } + \mathrm { V } _ { \mathrm { t } } \right) }
\]

The [OH^-] can be calculated by using an equation for a mixture of a weak base and a strong base, i.e.,

\[
\left[ \mathrm { OH } ^ { - } \right] = \mathrm { C } _ { \mathrm { s } }
\]

Example \(\PageIndex{7}\):

Consider the titration of a 50.0 mL solution of weak acid of butanoic (pK_a =4.98,i.e.,K_a =1.05x10^-5)ofconcentration0.10mol/Lwitha0.10mol/L standard NaOH solution. For convenience, we shall calculate only the pH of thesolution mixture in the titration flask.

Region 1: Before addition of NaOH, C_A = 0.10 mol/L.

\[
{ \left[ \mathrm { H } ^ { + } \right] = \left( \mathrm { K } _ { \mathrm { a } } \mathrm { C } _ { \mathrm { A } } \right) ^ { \frac { 1 } { 2 } } = \left\{ \left( 1.05 \times 10 ^ { - 5 } \right) ( 0.10 ) \right\} ^ { \frac { 1 } { 2 } } = 1.02 \times 10 ^ { - 3 } \mathrm { mol } / \mathrm { L } } \\ { \left[ \mathrm { OH } ^ { - } \right] = \frac { 1.00 \times 10 ^ { - 14 } } { 1.02 \times 10 ^ { - 3 } } = 9.77 \times 10 ^ { - 12 } \mathrm { mol } / \mathrm { L } }
\nonumber\]

Region 2: After addition of, say, 20.0 mL of NaOH. Total volume in the titra-tion flask becomes 70.0 mL and the solution is a mixture of a weak acid and its conjugate base.

\[
{ \mathrm { C } _ { a } = \frac { ( \text { moles of acid remaing } ) } { \text { Total volume } } = \frac { ( 0.050 \mathrm { L } ) ( 0.10 \mathrm { mol } / \mathrm { L } ) - ( 0.020 \mathrm { L } ) ( 0.10 \mathrm { mol } / \mathrm { L } ) } { ( 0.050 \mathrm { L } + 0.020 \mathrm { L } ) } = 0.0429 \mathrm { mol } / \mathrm { L } } \\ { \mathrm { C } _ { B } = \frac { ( 0.10 \mathrm { mol } / \mathrm { L } ) ( 0.020 \mathrm { L } ) } { 0.070 \mathrm { L } } = 0.0286 \mathrm { mol/L } \ \mathrm { C } \mathrm { B } }
\nonumber\]

Using the simplified equation for a mixture of a weak acid and its conjugate baseto solve for [H⁺] and therefore pH,

\[
\begin{aligned} \left[ H ^ { + } \right] = \frac { K _ { a } C _ { a } } { C _ { B } } & = \frac { \left( 1.05 \times 10 ^ { - 5 } \right) ( 0.0429 ) } { 0.0286 } = 1.57 \times 10 ^ { - 5 } \mathrm { mol } / \mathrm { L } \text { and } p H = - \log \left( 1.5 \times 10 ^ { - 5 } \right) = 4.80 \end{aligned}
\nonumber\]

\[
\left[ \mathrm { OH } ^ { - } \right] = \frac { 1.00 \times 10 ^ { - 14 } } { 1.57 \times 10 ^ { - 5 } } = 6.37 \times 10 ^ { - 10 } \mathrm { mol } / \mathrm { L }
\nonumber\]

Region 3: After addition of, say, 50.0 mL of NaOH. Total volume in the titrationflask becomes 100.0 mL and the solution contains only a weak base.

\[
{ C _ { B } = \frac { V _ { t } C _ { t } } { \left( V _ { A } + V _ { t } \right) } = \frac { ( 0.050 L ) ( 0.10 m o l / L ) } { 0.10 L } = 0.050 m o l / L } \\ { K _ { b } = \frac { 1.00 \times 10 ^ { - 14 } } { K_a } = 9.55 \times 10 ^ { - 10 } }
\nonumber\]

With the simplified equation for a weak base

\[
{ \left[ \mathrm { OH } ^ { - } \right] = \left( \mathrm { K } _ { \mathrm { b } } \mathrm { C } _ { \mathrm { B } } \right) ^ { \frac { 1 } { 2 } } = \left\{ \left( 9.55 \times 10 ^ { - 10 } \right) ( 0.050 ) \right\} ^ { \frac { 1 } { 2 } } = 6.91 \times 10 ^ { - 6 } \mathrm { mol } / \mathrm { L } } \\ { \left[ \mathrm { H } ^ { + } \right] = \frac { 1.00 \times 10 ^ { - 14 } } { 6.91 \times 10 ^ { - 6 } } = 1.45 \times 10 ^ { - 9 } \mathrm { mol } / \mathrm { L } , \text { and } \mathrm { pH } = - \log \left( 1.45 \times 10 ^ { - 9 } \right) = } { 8.84 }
\nonumber\]

Region 4: After addition of, say, 60.0 mL of NaOH. Total volume in the titrationflask becomes 110.0 mL and the solution contains both a weak base and a strong base.

Concentration of weak base,

\[
{C_w}=\frac { V _ { A } C _ { A } } { \left( V _ { A } + V _ { t } \right) } = \frac { ( 0.050 L ) ( 0.10 m o l / L ) } { 0.110 L } = 0.0455 \text { mol } / L
\nonumber\]

Concentration of strong base,

\[
C_s=\frac { \left( \mathrm { V } _ { \mathrm { t } } \mathrm { C } _ { \mathrm { t } } - \mathrm { V } _ { \mathrm { A } } \mathrm { C } _ { \mathrm { A } } )\right. } { \left( \mathrm { V } _ { \mathrm { A } } + \mathrm { V } _ { \mathrm { t } } \right) } = \frac { \{ ( 0.060 \mathrm { L } ) ( 0.10 \mathrm { mol } / \mathrm { L } ) - ( 0.050 \mathrm { L } ) ( 0.10 \mathrm { mol } / \mathrm { L } ) \} } { 0.110 \mathrm { L } }=0.00909\ mol/L
\nonumber\]

Using the simplified equation for a mixture of a strong and weak base,

\[
{ [ \mathrm { OH } ] = \mathrm { C } _ { \mathrm { s } } = 0.00909 \mathrm { mol } / \mathrm { L } } \\ { \left[ \mathrm { H } ^ { + } \right] = \frac { 1.00 \times 10 ^ { - 14 } } { 0.00909 } = 1.10 \times 10 ^{-12} \mathrm { mol } / \mathrm { L } , \text { and } \mathrm { pH } = - \log \left( 1.10 \times 10 ^{-12} \right) = 11.96 }
\nonumber\]

Note that the complete titration curve can be plotted when a series of additional calculations similar to those above are carried out.

Exercise \(\PageIndex{8}\): Titration of weak acid with strong base.

Using the information pro- vided below, plot the titration curve for the titration of 100.00 mL of 0.10 mol/L CH3COOH solution with 0.10 mol/L standard NaOH solution. Hint: Consider the four titration stages given above.

Answer

Illustration

Calculating pH at Initial Stage:

Let n moles of HA (i.e., a monoprotic weak acid such as the CH3COOH) be available in a titration flask. The pH is dependent on extent of dissociation of the weak acid. If K_a of the weak acid is very small (i.e., K_a < 1.0 x 10^-4), then it is possible to calculate the pH from the dissociation of weak acid using the relation:

\[
\mathrm { pH } = - \log \left[ \sqrt { \mathrm { K } _ { \mathrm { a } } [ \mathrm { Acid } ] }\right.
\]

Before equivalence point:

Again, let n moles of HA be available in titration flask. To this solution let mmoles of NaOH be added. In this titration, “Before Equivalence Point” meansn > m.

HA + NaOH → NaA + H2O

Start n m 0 0

n>m

Final n-m 0 m m

Question: What is left in the solution in the titration flask?

The solution left in the flask contains excess weak acid by an amount of (n-m) moles and salt of weak acid of an amount of equivalent to m moles. The solution is a buffer solution. Therefore, the pH of the solution can be calculated using the Henderson-Hasselbalch equation:
$$
\mathrm{pH}=\mathrm{pKa}+\log\frac{[\mathrm{salt}]}{[\mathrm{Acid}]}=\mathrm { pK } _ { \mathrm { a } } + \log \frac { \frac { \mathrm { m } } { \left( \mathrm { V } _ { \text { Acid } } + \mathrm { V } _ { \text { base added } } \right) } } { \frac { ( \mathrm { n } - \mathrm { m } ) } { \left( \mathrm { V } _ { \text { Acid } } + \mathrm { V } _ { \text { base added } } \right) } } = \mathrm { pK } _ { \mathrm { a } } + \log \frac { \mathrm { m } } { ( \mathrm { n } - \mathrm { m } ) }
\]

At equivalence point:

The acid is completely neutralized by the base added. Hence the pH is dependent on the salt solution. The resultant salt obtained is a salt of a weak acid and strong base. Therefore the anion part of the salt will hydrolyze as follows.

\[
\begin{array} { l } { \mathrm { NaA } \rightarrow \mathrm { Na } ^ { + } ( \mathrm { aq } ) + \mathrm { A } ^ { - } ( \mathrm { aq } ) } \\ { \mathrm { A } ^ { - } + \mathrm { H } _ { 2 } \mathrm { O } \Leftrightarrow \mathrm { HA } + \mathrm { OH } ^ { - } } \end{array}
\]

\[
\mathrm{pH}=\frac{1}{2}\{(\mathrm {pK_w}+\mathrm{pK_a}-\mathrm {pC_{salt \ produced}})\}= \frac { 1 } { 2 } \left\{ \left( \mathrm { pK } _ { \mathrm { w } } + \mathrm { pK } _ { \mathrm { a } } + \log \left( \frac { \mathrm { m } } { \mathrm { V } _ { \text { arid } } + \mathrm { V } _ { \text { base } } } \right) \right\}\right.
\]

After equivalence point:

The amount of strong base added is more than the amount required to neutralize the acid. Hence an excess amount of strong base will remain in solution. The pH can be calculated from the excess strong base left in the solution using the following equation.

\[
\mathrm { pH } = \mathrm { pK } _ { \mathrm { w } } + \log[\frac{\mathrm(C_{Base}V_{base\ added})-(C_{Acid}V_{acid})}{(V_{acid}+V_{base\ added})}]
\]

Exercise \(\PageIndex{9}\): Titration of weak acid with strong base.

Plot a titration curve for titrating 75 mL of 0.12 mol/L CH3COOH with 0.09 mol/L NH₃. K_a for CH₃COOH= 1.8 x 10^-5 and K_b for NH₃ = 1.8 x 10^-5. Hint: Consider the four titration stages discussed earlier.

Answer

Polyprotic Acids:

In our previous discussion of acid-base reactions, we dealt with acids (e.g., HCl, HNO₃, and HCN) that contain only one ionizable hydrogen atom in each molecule. This group of acids that have only one ionizable hydrogen atom per molecule is known as monoprotic acid. The corresponding reactions of the monoprotic acids given above with a base like water are as follows:

HCl + H₂O → H₃O⁺ + Cl^-

HNO₃ + H₂O → H₃O⁺ + NO₃^-

HCN + H₂O ↔ H₃O⁺ + CN^-

HNO₃ + H₂O → H₃O⁺ + NO₃^-

HCN + H₂O ↔ H₃O⁺ + CN^-

In general, however, acids can be classified by the number of protons present permolecule that can be given up in a reaction. For acids that can transfer more than one proton to a base, the term polyprotic acid is used. Diprotic acids contain two ionizable hydrogen atoms per molecule and their ionization occurs in two stages. Examples of diprotic acids include, H₂SO₄, H₂S, H₂CO₃, etc. An illustration of the two-stage ionization of H₂S is as follows:

H₂S + H₂O ⇌H₃O⁺ + HS^- (primary ionization)

HS^- + H₂O ⇌ H₃O⁺ + S^2- (secondary ionization)

Each of the above steps is characterized by a different acid ionization constant.

The primary ionization step has an acid ionization constant,

\[
\mathrm { K } _ { 1 } = \frac { \left[ \mathrm { HS } ^ { - } \right] \left[ \mathrm { H } _ { 3 } \mathrm { O } ^ { + } \right] } { \left[ \mathrm { H } _ { 2 } \mathrm { S } \right] }
\]

whereas the secondary has an acid ionization constant,

\[
\mathrm { K } _ { 2 } = \frac { \left[ \mathrm { S } ^ { 2 - } \right] \left[ \mathrm { H } _ { 3 } \mathrm { O } ^ { + } \right] } { \left[ \mathrm { HS } ^ { - } \right] }
\]

If K₁ ≈ K₂, the two steps occur simultaneously and both must be considered in solving any problems involving the pH of solutions of the acid. If however,

K₁ ≫ K₂ (by atleast a factor of 10⁴), then only the one reaction involving the species present need be considered. This then makes one apply the simple monobasic equations that have been dealt with previously in unit 2.

Of the two steps above, the primary ionization always takes place to a greater extent than the secondary ionization.

The most common triprotic acid is phosphoric acid or sometimes called ortho-phosphoric acid (H₃PO₄), which can ionize in solution in three steps as follows:

H₃PO₄ + H₂O ⇌H₃O⁺ + H₂PO₄^- (primary ionization)

H₂PO₄^- + H₂O ⇌ H₃O⁺ + H₂PO₄^2- (secondary ionization)

H₂PO₄^2- + H₂O ⇌ H₃O⁺ + H₂PO^3- (tertiary ionization)

The corresponding experimentally determined acid ionization constants for phosphoricacid (H₃PO₄) are: K₁ =7.5×10^-3, K₂ =6.6×10^-6, and K₃ =1.0×10^-12

Thus, a solution of phosphoric acid will usually comprise a mixture of three different acids; H₃PO₄, H₂PO₄^- , and HPO₄^2- and their corresponding conjugate bases.

It is important to note that successive ionization constants for a given acid gene- rally have widely different values as can be seen in the case of phosphoric acid (i.e., K₁ >> K₂ >> K₃). Thus, as mentioned in the case of the diprotic acid above, no more than two of the successive species associated with the ionization of a particular polyprotic acid are present in significant concentrations at any particular pH. Hence, the equilibria or any calculations can be determined by only one, or at most two,of the acid ionization constants.

Titration of a Polyprotic Weak acid with a Strong base

In accordance with the stepwise dissocitation of di- and polyprotic weak acids, their neutralization reactions are also stepwise. For instance, in the titration of orthophosphoric acid (H₃PO₄) with a strong base such as NaOH, the following stepwise reactions occur:

H₃PO₄ + NaOH ↔ NaH₂PO₄ + H₂O

NaH₂PO₄ + NaOH → NaH₂PO₄ + H₂O

Na₂HPO₄ + NaOH ↔ Na₃PO4 + H₂O

Accordingly, the H₃PO₄–NaOH titration curve has not one but three equivalence points. The first equivalence point is reached after one mole of NaOH has beenadded per mole of H₃PO₄; the second after addition of two moles of NaOH; andthe third after addition of three moles of NaOH.

Example \(\PageIndex{8}\):

If 10.00 mL of 0.10 mol L-1 H₃PO₄ solution is titrated, the first equivalence point is reached after addition of 10.00 mL, the second after addition of 20.00 mL, and the third after addition of 30.00 mL of 0.10 mol L-1 NaOH solution.

Titration of a Diprotic weak acid (H₂A) with NaOH

For a diprotic weak acid represented by H₂A,
1. The pH at the beginning of the titration is calculated from the ionization (dissocitation) of the first proton, i.e.,

H₂A⇌H⁺ +HA^-

If K_a1, the acid dissociation constatant$$
(= \frac { \left[ \mathrm { H } ^ { + } \right] \left[ \mathrm { HA } ^ { - } \right] } { \left[ \mathrm { H } _ { 2 } \mathrm { A } \right] } )
\nonumber$$, is not too large and amount of dissociated H2A is ignored compared to the analytical concentration of the acid, then

\[
\left[ \mathrm { H } ^ { + } \right] = \sqrt { \mathrm { K } _ { \mathrm { al } } \left[ \mathrm { H } _ { 2 } \mathrm { A } \right] }
\]

Otherwise the quadratic formula must be used to solve pH (see section on .... Of unit 2).

2. The pH during titration upto the first equivalence point

An HA^-/H₂A buffer region (a region where the solution attempts to resist any change in pH upon addition of base during the titration) is established such that

\[
\mathrm { pH } = \mathrm { pK } _ { \mathrm { al } } + \log \left( \frac { \mathrm { HA } ^ { - } } { \mathrm { H } _ { 2 } \mathrm { A } } \right)
\]

3. At the first equivalence point

$$
\mathrm { pH } = \frac { \mathrm { pK } _ { \mathrm { al } } + \mathrm { pK } _ { \mathrm { a } 2 } } { 2 }
$$

4. Beyond the first equivalence point an A2-/HA- buffer exists

\[
\mathrm { pH } = \mathrm { pK } _ { \mathrm { a } 2 } + \log \left( \frac { \left[ \mathrm { A } ^ { 2 - } \right] } { \left[ \mathrm { HA } ^ { - } \right] } \right)
\]

5. At the second equivalence point the pH is determined from the hydrolysis of A^2- salt (i.e., A^2- + H₂O ⇌ HA^- + OH^-), such that

$$
\left[ \mathrm { OH } ^ { - } \right] = \sqrt { \frac { \mathrm { K } _ { w } } { \mathrm { K } _ { \mathrm { a } 2 } } \left[ \mathrm { A } ^ { 2 - } \right] }
$$

6. Beyond the second equivalence point

The pH will be dependent on the concentration of excess strong base added (i.e., concentration of the titrant).

Illustration:

Consider addition of sodium hydroxide solution to dilute ethanedioic acid (oxalic acid). Ethanedioic acid is a diprotic acid which means that it can give away 2 protons (hydrogen ions) to a base. (Note that something which can only give away one (like HCl) is known as a monoprotic acid).

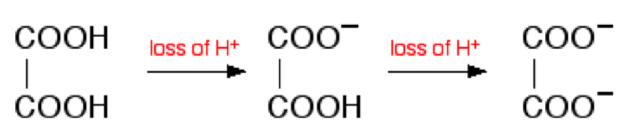
The reaction with NaOH takes place in two stages because one of the hydrogens is easier to remove than the other. The two successive reactions can be represented as:

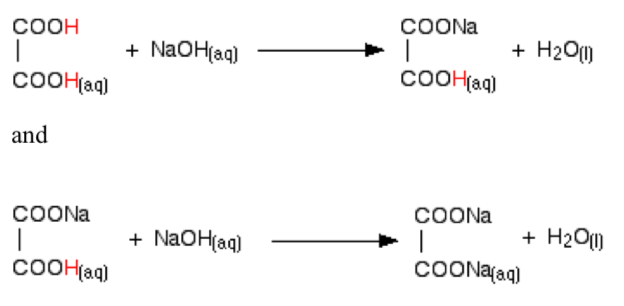
By running NaOH solution into ethanoic acid solution, the pH curve shows the end points for both of these reactions as shown in the figure below.

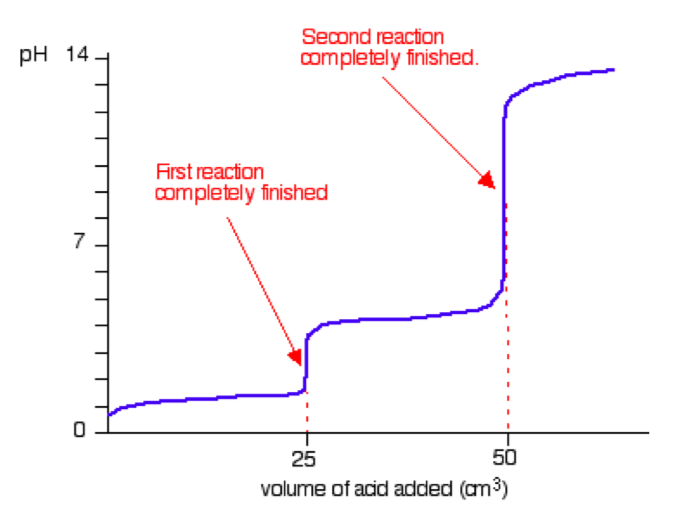
The curve is the reaction between NaOH and ethanedioic acid solutions of equal concentrations.

Exercise \(\PageIndex{10}\)

Plot a titration curve for the titration of 75 mL of 0.12 mol L^-1 H₂CO₃ with 0.09 mol L^-1 NaOH, given that K_al = 4.3 x 10^-7 and K_a2 = 5.6 x 10^-11.

Hint: You are expected to consider the six titration stages shown above to collect data in order to plot the titration curve.

Answer

Exercise \(\PageIndex{11}\)

In the titration of a triprotic acid, H₃A with NaOH where K_a1/K_a2 ≥104andK/K ≥10⁴,

(a) Identify the eight titration stages that need to be considered in order to plot the corresponding titration curve.

(b) Derive the expressions for pH in each of the eight stages.

Answer

Titration of Anions of a weak acid with strong acid, HA

For the titration of Na₂A salt:

1. The pH at the beginning of the titration is calculated from the hydrolysis of A^2- salt i.e.,

   A^2- + H₂O ⇌ HA^- + OH^-

2. During the titration up to the first equivalence point

   A^2- + H+ ⇌ HA^-

   The solution mixture of HA- and A2- is a buffer solution and so,

   \[
   \mathrm { pH } = \mathrm { pK } _ { \mathrm { a } 2 } + \log \frac { \left[ \mathrm { A } ^ { 2 - } \right] } { \left[ \mathrm { HA } ^ { - } \right] }
   \]

3. At the first equivalence point

   A^2- + H⁺ ⇌ HA^-

   We have HA^- in solution and pH arises from the dissociation of HA^-, i.e.,

   HA^- + H₂O ⇌ H₃O⁺ + A^2- and

   \[
   \mathrm { pH } = \frac { \mathrm { pK } _ { \mathrm { al } } + \mathrm { pK } _ { \mathrm { a } 2 } } { 2 }
   \]

4. Beyond the first equivalence point:

   HA^- + H⁺ ⇌ H₂A

   The resultant solution is a mixture of H A and HA-, hence a buffer solution and so

   \[
   \mathrm { pH } = \mathrm { pK } _ { \mathrm { al } } + \log \frac { \left[ \mathrm { HA } ^ { - } \right] } { \left[ \mathrm { H } _ { 2 } \mathrm { A } \right] }
   \]

5. At second equivalence point:

   HA^- + H⁺ ⇌ H₂A

   Here, only H₂A is left in solution and hence pH is dependent on the dissociation of H₂A, and so

   H₂A + H₂O ⇌ H₃O⁺ + HA^-

   \[
   \left[ \mathrm { H } ^ { + } \right] = \sqrt { \mathrm { K } _ { \mathrm { al } } \left[ \mathrm { H } _ { 2 } \mathrm { A } \right] }
   \]

6. Beyond the second equivalence point:

   Excess strong acid is added and the pH is determined by the concentration of excess strong acid.

Exercise \(\PageIndex{12}\)

Plot the titration curve of 75mL of 0.12 mol L^-1 CH COONa with 0.09 mol L^-1 HCl. K_a for CH₃COOH = 1.80 x 10^-5. Hint: Consider the four possible titration stages.

Answer

Add texts here. Do not delete this text first.

Exercise \(\PageIndex{13}\)

Plot the titration curve of 75mL of 0.12 mol L^-1 Na₂CO₃ with 0.09 mol L^-1 HCl. K_a1 = 4.3 x 10^-7 and K_a2 = 5.6 x 10^-11. Hint: You are expected to consider six possible titration stages to collect data in order to plot the titration curve.

Answer

Acid-Base Indicators

Example \(\PageIndex{9}\):

In the titration of 30.0 mL of 0.10 M HF with 0.20 M KOH, the pH of the solution mixtures at 10.0, 15.0, and 20.0 mL additions of the strong alkali are 3.76, 8.14, and 12.30, respectively. If phenol red (whose pK value is 7.5 and its acid colour is yellow and its base colour is red) were to be used as an indicator for the titration reaction, what colour would the indicator be at the 10, 15, and20 mL additions of KOH?

Solution

At 10 mL, the pH is 3.76. This is very acidic; the colour will be yellow.

At 15 mL, the pH is 8.14. This is just within the of the pK, so it will be orange. Likely a reddish-orange colour.

At 20 mL, the pH is 12.30. This is very basic; and hence the colour will bered.

Since it changes colour at the equivalence point (it doesn’t have to hit exactly), this would be a reasonable choice indicator.

Exercise \(\PageIndex{14}\)

Refer to the example above. The indicator methyl orange has a pK of about 3.5. It is red in its acidic form and yellow in its basic form. What colourwill the indicator be at 10, 15, and 20 mL additions of KOH? Would this be a good indicator for this titration?

Answer