14.4: Complex ion Equilibria and Complexometric Titrations
- Page ID
- 134632
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Define and use the relevant terminologies of complex ion equilibria
- Compare and contrast between complex ion and Lewis acid-base equilibria
- Describe and explain the concept of complex equilibria and stepwise equilibrium reactions.
- Use the concept of chemical equilibria in complexometric titrations and calculations.
- Distinguish among the various types of EDTA titrations and their uses.
- Carry out complexometric titrations and related calculations.
In this unit, the concept of complex ion formation and associated stepwise equilibrium reactions will be examined and discussed. Particular emphasis will be given to the application of the complex ion reactions in complexometric titrations, titrimetric methods based upon complex formation, as a means to quantitative analysis of metal ions in solution. The emphasis will be on how complex ion formation can be used as a basis of a titrimetric method to quantify metal ions in solution. Here, ethylenediamine tetraacetic acid (EDTA) will be studied as an analytical reagent or titrant that forms very stable complexes with many metal ions in complexometric titration. EDTA (a tertiary amine that also contains carboxylic acid groups) is the most widely used polyaminocarboxylic acid. A discussion of the factors that influence the stability of metal-EDTA complexes and their significance as well as the types of EDTA titrations will also be covered.
Key Concepts
- Acid-base indicators: acids or bases which exhibits a visual change on neutrali- zation by the basic or acidic titrant at or near the equivalence point.
- Chelation: the process involved in formation of a chelate.
- Chemical stoichiometry: measurement based on exact knowledge of chemical combination
- Colorimetric indicator: intensely coloured substances in atleast one form (bound or unbound to a metal) and do change colour when the metal ion analyte binds with it.
- Complex: a substance composed of two or more components capable of an in- dependent existence.
- Complexation: the association of two or more chemical species that are capable of independent existence by sharing one or more pairs of electrons.
- Complexometric indicator: water soluble organic molecules that undergoedefinite colour change in the presence of specific metal ions and are used incomplexometric titrations.
- Complexometric titration: A titration based on the formation of coordination complexes between a metal ion and complexing agent (or chelating agent) to form soluble complexes.
- Complexing agent or ligand: molecules and/or anions with one or more donor atoms that each donate a lone pair of electrons to the metal ion to form a covalent bond.
- Coordination complex: a complex in which a central atom or ion is joined to one or more ligands through what is formally a coordinate covalent bond in which both of the bonding electrons are supplied by a ligand.
- Metal chelate: a species that is simultaneously bound to two or more sites on a ligand.
- Monodentate (or Unidentate) ligand: A ligand that shares a single pair of elec- trons with a central metal ion in a complex.
- Multidentate ligand: A ligand which shares more than one pair of electrons with a central metal ion in a complex. Those ligands which share 2, 3, 4, 5, or 6 are referred to as bidentate, tridentate, tetradentate (or quadridentate), pentadentate (or quinqui dentate), and hexadentate, respectively.
- Stability constant of a complex: a measure of the extent of formation of the complex at equilibrium.
Introduction
Complex-forming reactions involving many metal ions can serve as a basis for accurate and convenient titrations for such metal ions. These kinds of complex ion titration procedures referred to as complexometric titrations, have high ac- curacies and offer the possibility of determinations of metal ions at the millimole levels. They have their applications in many chemical and biological processes. The processes involved in the formation of complex ions are basically acid-base type reactions in which the metal ion acts as an acid and the anions or molecules as the base (see unit 2 that deals with acids and bases). In this activity, the theoryand applications of complex ion formation, and specifically complexometric ti- trations in quantifying metal ions in solution will be examined. In addition, thesignificance of using a reagent that forms a chelate over one that merely forms acomplex with a metal ion in volumetric analysis will be explained. Since much attention has recently been focused on the use of ethylenediamine tetraacetic acid (EDTA) in titrimetry, its various applications will be highlighted in this unit.
Introduction to Complexation Equilibria and Processes
In this introduction, important terminologies that will be encountered when dealing with the topic of complexation titration are provided. Also included is a brief description of what a complex is and how their very nature contrast Lewis acid-base systems.
In the broadest sense, complexation is the association of two or more chemical species that are capable of independent existence by sharing one or more pairs of electrons. Although this type of a chemical reaction can be classified as a Lewis acid-base reaction, it is more commonly known as a complexation reaction. As applied to chemical analysis, this definition is generally taken to mean the bonding of a central metal ion, capable of accepting an unshared pair of electrons with a ligand that can donate a pair of unshared electrons.
Consider the addition of anhydrous copper (II) perchlorate to water. The salt dissolves readily according to the reaction,
\[\ce{Cu(ClO4)2 (s) + 4H:O:H -> Cu(H2O)4^{2+} (aq) + 2ClO4^{-}}\]
in which a pair of electrons on the oxygen atom of each H2O molecule forms a coordinate covalent bond, a bond in which both electrons originate from one atom(in this case one oxygen atom of H2O), to Cu2+ ion. In this reaction, Cu2+ acts as a Lewis acid and H2O as a Lewis base. Such binding of solvent molecules to a metal ion is called solvation or, in the special case of solvent water, hydration. The Cu(H2O)42- ion is called an aquo complex.
In a complexation reaction, the product of the reaction is termed a complex. The species which donates the electron pairs by acting as a Lewis base is known as a complexing agent or ligand, and the ion which accepts the donated electrons, theLewis acid, is called the central ion or central atom. Central ions are generally metallic cations. The ligand can be either a neutral molecule such as water orammonia; or an ion such as chloride, cyanide, or hydroxide. The complex can have either a positive or a negative charge, or it can be neutral.
For most analytical applications, complexation occurs between a dissolved metal ion and a dissolved ligand capable of displacing water from the metal ion. This is illustrated for the reaction between a hydrated copper (II) ion and dissolved NH3 ligand below.
\(\
\left[ \mathrm { Cu } \left( \mathrm { H } _ { 2 } \mathrm { O } \right) _ { 4 } \right] ^ { 2 + } + \mathrm { NH } _ { 3 } \stackrel { \mathrm { water } } { \longrightarrow } \left[ \mathrm { CuNH } _ { 3 } \left( \mathrm { H } _ { 2 } \mathrm { O } \right) _ { 3 } \right] ^ { 2 + } + \mathrm { H } _ { 2 } \mathrm { O }
\)
Normally for reactions that occur in water, \(\ce{H2O}\) is omitted and the complexation reaction is written simply a
\[\ce{Cu^{2+} + NH3 <=> [CuNH3]^{2+}}\]
Classification of Ligands
Ligands are classified according to the number of pairs of electrons which theycan share with the central metal or metal ion. A ligand that shares a single pair of electrons (such as ammonia, water, cyanide, F-, Cl-, Br-, I-, CN-, SCN-, NO2-, NH3, H2O, N(CH2CH3)3, CH3COCH3, etc.) is a monodentate or unidentate ligand; a ligand, which shares more than one pair of electrons, is a multidentate ligand. A multidentate ligand, which shares two (such as NH2CH2CH2NH2, C2O42-, etc,), three, four, five, or six pairs of electrons is a bidentate, tridentate (or terdentate), tetradentate (or quadridentate), pentadentate (or quinqui dentate), or hexadentate (or sexadentate) ligand, respectively. The maximum number of electron pair donor groups that a metal ion can accommodate in complexation reaction is known as its coordination number. Typical values are 2 for Ag+, as in Ag(CN)2-, 4 for Zn2+, as in Zn(NH3)42+; and 6 for Cr3+, as in Cr(NH3)63+.
Nature of Linkage in complex ions
A central metal ion can form a single bond with a ligand which is able to donate a pair of electrons from one of its atoms only, as in the examples given above for the formation of Zn(NH3)42+, Cr(NH3)63+ etc. However, with multidentate (or sometimes known as polydentate) ligands, it can form a bond in more than one location to form a ring structure. Generally, ring formation results in increased stability of the complex. A species that is simultaneously bonded to two or more sites on a ligand is called a metal chelate, or simply a chelate and the process of its formation is called chelation.
A chelate is formed if two or more donor atoms is coordinated by the simulta- neous use of two or more electron pairs to the same metal atom. An example ofa metal-EDTA complex is provided in the figure below.
Note that, all types of bidentate, tridentate, tetradentate, pentadentate and hexa- dentate ligands can act as chelating ligands and their complexes with metals are therefore known as chelates.
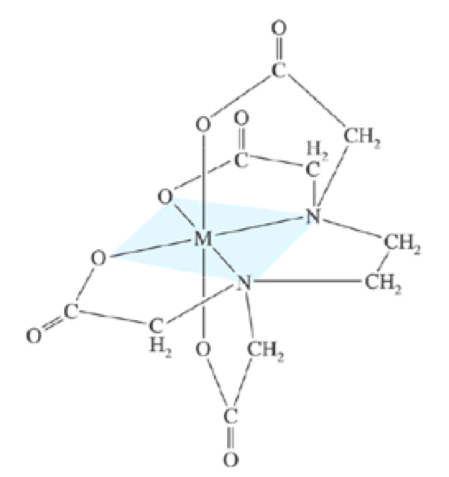
Here, EDTA behaves as a hexadentate ligand since six donor groups are involved in bonding the divalent metal cation.
Importance of Chelates
Chelates find application both in industry and in the laboratory where fixing ofmetal ions is required. In analytical chemistry, chelates are used in both qualitative and quantitative analysis. For example, Ni2+, Mg2+, and Cu2+ are quantitatively precipitated by chelating agents. In volumetric analysis, chelating agents (such as ethylenediamine tetraacetic acid, EDTA) are often used as a reagents or as indicators for the titration of some metal ions. Because of the stability of chelates, polydentate ligands (also called chelating agents) are often used to sequester or remove metal ions from a chemical system. Ethylenediamine tetraacetic acid (EDTA), for example, is added to certain canned foods to remove transition-metal ions that can catalyze the deterioration of the food. The same chelating agent has been used to treat lead poisoning because it binds Pb2+ ions as the chelate, which can then be excreted by the kidneys.
In the subsequent sections that follow, the application of the fundamentals of complex ion formation is demonstrated in complexometric titration. This isachieved after briefly considering the subtopic of complex equilibria.
Complex ion Equilibria
Stability constant of a complex is defined as a measure of the extent of formation of the complex at equilibrium. Stability of a complex depends on the strength of the linkage between the central metal ion and the ligands (ie., the bond) and therefore, the stronger the metal ligand bond, the more stable the complex.
Metal complexes are formed by replacement of molecules in the solvated shell of a metal ion in aqueous solution with the ligands by stepwise reaction as shown below:
[M(H2O)2] + L ⇌ [M(H2O)n-1L] + H2O
[M(H2O)n-1L] + L ⇌ [M(H2O)n-2L2] + H2O
[M(H2O)n-2L2] + L ⇌ [M(H2O)n-3L3] + H2O
Overall reaction is:
[M(H2O)n] + nL ⇌ [MLn] + nH2O
where L stands for the ligand and n refers to the number of molecules of a parti- cular species. If we ignore the water molecules in the above equations, one can then write the above equations and their corresponding equilibrium constants as follows:
M + L ⇌ ML \(\ \bf{K}_1=\dfrac{[ML]}{[M][L]}\)
ML + L ⇌ ML2 \(\ \bf{K}_2=\dfrac{[\bf{ML}_2]}{[ML][L]}\)
ML2 + L ⇌ ML3 \(\ \bf{K}_3=\dfrac{[\bf{ML}_3]}{[\bf{ML}_2][L]}\)
MLn-1 + L ⇌ MLn \(\ \bf{K}_n=\dfrac{[\bf{ML}_n]}{[\bf{ML}_{n-1}][L]}\)
The equilibrium constants, K1, K2, K3, ...., and Kn are known as the stepwise formation constants or stepwise stability constants or consecutive stability constants.
Note that the values of the stepwise stability constants decrease in the order:
K1 >K2 >K3 >...>Kn
because a previously metal ion-coordinated ligand tends to repel any incoming ligand of a similar kind.
The products of the stepwise stability constants is known as overall stability or cumulative stability constant and is designated as \(β\), i.e.,
\[β=K_1 \times K_2 \times K_3 \times ... \times K_n\]
\(\
\beta = \frac { [ \mathrm { ML } ] } { [ \mathrm { M } ] [ \mathrm { L } ] } \cdot \frac { \left[ \mathrm { ML } _ { 2 } \right] } { [ \mathrm { ML } ] [ \mathrm { L } ] } \cdot \frac { \left[ \mathrm { ML } _ { 3 } \right] } { \left[ \mathrm { ML } _ { 2 } \right] [ \mathrm { L } ] } \cdots \cdot \frac { \left[ \mathrm { ML } _ { \mathrm { n } } \right] } { \left[ \mathrm { ML } _ { n - 1 } \right] [ L ] }
\)
As previously mentioned, multidentate ligands which form five- or six-member red rings with central metal ions, generally have unusually high stability. To be useful in a titration, the complexation reaction must occur rapidly as compared with the rate of addition of the titrant. Complexes which are formed rapidly are called labile complexes and those which are formed slowly are called nonla-bile or inert complexes. Generally, only titration reactions which form labile complexes are useful.
Consider the simple complexation of copper (II) ion by the unidentate ligand NH3 in water. The reaction between these two species is
\[\ce{Cu^{2+} + NH3 <=> [CuNH3]^{2+}}\]
(the H2O is omitted for simplicity). In aqueous solution the copper (II) ion is actually hydrated and NH3 replaces H2O. The equilibrium constant for this reaction is the stepwise formation constant, K1, is expressed as:
\(\
\mathrm { K } _ { 1 } = \frac { \left[ \left[ \mathrm { CuNH } _ { 3 } \right] ^ { 2 + } \right] } { \left[ \mathrm { Cu } ^ { 2 + } \right] \left[ \mathrm { NH } _ { 3 } \right] } = 2.0 \times 10 ^ { 4 }
\)
The equilibrium of the addition of a second ammonia molecule,
CuNH32+ + NH3 ⇌ [Cu(NH3)2 ]2+
is described by a second stepwise formation constant, \(K_2\),
\(\
\mathrm { K } _ { 2 } = \frac { \left[ \left[ \mathrm { Cu } \left( \mathrm { NH } _ { 3 } \right)_2 \right] ^ { 2 + } \right] } { \left[ \mathrm { CuNH } _ { 3 } \right] ^ { 2 + } ] \left[ \mathrm { NH } _ { 3 } \right] } = 5.0 \times 10 ^ { 3 }
\)
The overall process for the addition of the two NH3 molecules to a Cu2+ ion and the equilibrium constant for that reaction are given by the following:
Cu2+ + NH3 ⇌ [CuNH3 ]2+
\(\
\mathrm { K } _ { 1 } = \frac { \left[ \left[ \mathrm { CuNH } _ { 3 } \right] ^ { 2 + } \right] } { \left[ \mathrm { Cu } ^ { 2 + } \right] \left[ \mathrm { NH } _ { 3 } \right] } = 2.0 \times 10 ^ { 4 }
\)
CuNH32+ + NH3 ⇌ [Cu(NH3)2]2+
\(\
\mathrm { K } _ { 2 } = \frac { \left[ \left[ \mathrm { Cu } \left( \mathrm { NH } _ { 3 } \right) _ { 2 } \right] ^ { 2 + } \right] } { \left[ \mathrm { CuNH } _ { 3 } \right] ^ { 2 + } ] \left[ \mathrm { NH } _ { 3 } \right] } = 5.0 \times 10 ^ { 3 }
\)
Cu2+ + 2NH3 ⇌ [Cu(NH3)2 ]2+
\(\
\beta _ { 2 } = \frac { \left[ \left[ C u \left( \mathrm { NH } _ { 3 } \right) _ { 2 } \right] ^ { 2 + } \right] } { \left[ C u ^ { 2 + } \right] ] \left[ N H _ { 3 } \right] ^ { 2 } } = K _ { 1 } \times K _ { 2 } = 1.0 \times 10 ^ { 8 }
\)
The formation constant β2 (= K1K2) is called an overall formation constant. Recall that the equilibrium constant of a reaction obtained by adding two other reactions is the product of the equilibrium constants of these two reactions, β2.
Similarly, the stepwise and overall formation constant expressions for the complexation of a third and fourth molecule of NH3 to copper (II) are given by the following:
[Cu(NH3)2 ]2+ + NH3 ⇌ [Cu(NH3)3]2+ \(\ \mathrm { K } _ { 3 } = \frac { \left[ \left[ \mathrm { Cu } \left( \mathrm { NH } _ { 3 } \right) _ { 3 } \right] ^ { 2 + } \right] } { \left[ \left[ \mathrm { Cu } \left( \mathrm { NH } _ { 3 } \right) _ { 2 } \right] ^ { 2 + } \right] \left[ \mathrm { NH } _ { 3 } \right] }
\)
[Cu(NH3)3 ]2+ + NH3 ⇌ [Cu(NH3)4]2+ \(\ \mathrm { K } _ { 4 } = \frac { \left[ \left[ \mathrm { Cu } \left( \mathrm { NH } _ { 3 } \right) _ { 4 } \right] ^ { 2 + } \right] } { \left[ \left[ \mathrm { Cu } \left( \mathrm { NH } _ { 3 } \right) _ { 3 } \right] ^ { 2 + } \right] \left[ \mathrm { NH } _ { 3 } \right] }
\)
Cu2+ + 4NH3 ⇌ [Cu(NH3)4]2+
\(\
\beta _ { 4 } = \frac { \left[ \left[ \mathrm { Cu } \left( \mathrm { NH } _ { 3 } \right)_4 \right] ^ { 2 + } \right] } { \left[ \mathrm { Cu } ^ { 2 + } \right] ] \left[ \mathrm { NH } _ { 3 } \right] ^ { 4 } } = \mathrm { K } _ { 1 } \times \mathrm { K } _ { 2 } \times \mathrm { K } _ { 3 } \times \mathrm { K } _ { 4 }
\)
The values of K3 and K4 are 1.0 x 103 and 2.0 x 102, respectively. Therefore, the values of β3 and β4 are 1.0 x 1011 and 2.0 x 1013, respectively.
The stepwise formation constants of the amine complexes of copper (II) are rela- tively close together. This means that over a wide range of NH3 concentrations, there will exist at the same time, at least two (normally more), copper (II) aminecomplexes in solution at significant concentrations relative to each other. This isgenerally true of unidentate ligands and hence limits their use as titrants for the determination of metal ions (save for a few specialized cases, which is beyond the scope of this module).
A major requirement for titration is a single reaction that goes essentially to completion at the equivalence point. This requirement is generally not met by unidentate ligands because of the fact that their formation constants are not very high.
Dissociation of Complexes
A given complex behaves as a weak electrolyte and dissociates to a small degree. The equilibrium constant for the dissociation of a complex is simply the inverse of its formation constant, Kform, and is known as the instability constant, Kins. For example, the complex ion Ag(NH3)2+ dissociates according to the equilibrium reaction:
[Ag(NH3)2 ]+ ⇌ Ag+ + 2NH3
and its instability constant is given by,
\(\
\mathrm { K } _ { \mathrm { ins } } = \frac { 1 } { \mathrm { K } _ { \mathrm { form } } } = \frac { \left[ \mathrm { Ag } ^ { + } \right] \left[ \mathrm { NH } _ { 3 } \right] ^ { 2 } } { \left[ \mathrm { Ag } \left( \mathrm { NH } _ { 3 } \right) _ { 2 } ^ { + } \right] }
\)
In actual practice, the dissociation of a complex ion, just like the ionization of a polyprotic acid, occurs in steps as shown below:
Ag(NH3)2+ ⇌ Ag(NH3)+ + NH3 \(\
\mathrm { K } _ { 1 } = \frac { \left[ \mathrm { Ag } \left( \mathrm { NH } _ { 3 } \right) ^ { + } \right] \left[ \mathrm { NH } _ { 3 } \right] } { \left[ \mathrm { Ag } \left( \mathrm { NH } _ { 3 } \right) _ { 2 } ^ { + } \right] }
\)
Ag(NH3)+ ⇌ Ag+ + NH3 \(\
\mathrm { K } _ { 2 } = \frac { \left[ \mathrm { Ag } ^ { + } \right] \left[ \mathrm { NH } _ { 3 } \right] } { \left[ \mathrm { Ag } \left( \mathrm { NH } _ { 3 } \right) ^ { + } \right] }
\)
The overall instability constant, Kins = K1 x K2
Calculate the percent dissociation of a 0.10 M Ag(NH3)2+ solution if its instability constant, Kins = 6.3 x 10-8.
- Answer
Application of Complex Equilibria in Complexation Titration:
The concept behind formation of complexes can be used as stated earlier (see section on importance of chelates), in quantitative analysis of either metal ions or other anions of interest.
An example to illustrate the use of complex titration exercise is in the determi- nation of cyanide present in a solution via the titration of cyanide with silver nitrate solution given below.
When a solution of silver nitrate is added to a solution containing cyanide ion(alkali cyanide), a white precipitate is formed when the two ligands first comeinto contact with each another. On stirring, the precipitate re-dissolves due to the formation of an alkali stable salt of silver-cyanide complex, i.e.,
Ag+ + 2CN- ⇌ [Ag(CN)2]-
When the above reaction is complete (following attainement of an equivalence point), further addition of the silver nitrate solution now yields an insoluble silver cyanoargentate (some times termed insoluble silver cyanide). The end point of the reaction is indicated by the formation of a permanent precipitate or turbidity. Such a titration experiment can be used to quantify the amount of cyanide present in a solution. Here cyanide is an example of a complexone; another term for a complexing agent.
Note that the formation of a single complex species in contrast to a stepwiseproduction of complex species simplifies complexation titration (i.e., complexo- metric titrations) and facilitates the detection of end points.
The chelate most commonly used for complexometric titrations is ethylenedia- mine tetraacetic acid (EDTA); an aminopolycarboxylic acid which is an excel- lent complexing agent. It is normally represented by either of the following two structures:
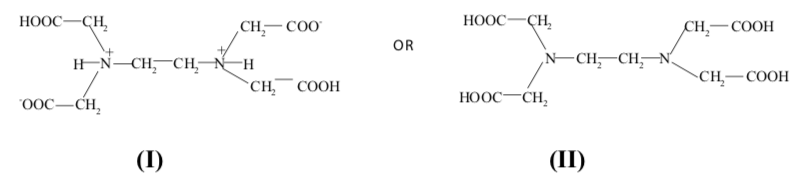
Its greatest advantage is that it is inexpensive, chemically inert, and it reacts with many metals with a simple stoichiometry
EDTA4- +Mn+ → [M−EDTA]n-4
where n is the charge on the metal ion, M.
This complexing agent has four (4) ionizable acid groups with the following pKa(= -logKa, where Ka is the acid dissociation constant) values: pKa1 = 2, pKa2 = 2.7,pKa3 = 6.6 and pKa4 = 10.3 at 20°C. These values suggest that the complexing agent behaves as a dicarboxylic acid with two strongly acidic groups and thatthere are two ammonium protons of which the first ionizes in the pH region ofabout 6.3 and the second at pH of about 11.5.
If Mn+ is the metal ion and Y4- stands for the completely ionized form of EDTA, then the metal-EDTA complex can be represented as MY(n-4)+. The stability of such a complex is often dependent on a number of factors, that need due consi- deration as one investigates the application of EDTA titration experiments inquantification of metal ions in solution. These factors affect the various multiple equilibria shown above, which in turn influences how complexometric titrationis carried out. The next section looks at the two important factors that are true for all complexometric titrations.
Factors affecting Stability of Metal-EDTA complexes
- Effect of pH on stability of metal-EDTA complexes
The concentration of each of the complexes shown, say in examples above, will depend on the pH of the solution. So to have any properly defined equilibria,the pH of the solution mixture will have to be buffered. Equally important, the concentration of protons, H+, which would otherwise compete with the Mn+ ions, must be held rigorously constant. For instance, at low pH values protonation(the act of transferring or donating a proton, a hydrogen ion, H+, to a species) of Y4- species occurs and the species HY3-, H2Y2-, H3Y- and even undissociated H4Y may well be present. (The abbreviations H4Y, H3Y-, H2Y2-, HY3-, and Y4- are often used to refer to EDTA and its ions.) Thus, the act of lowering the pH of the solution will decrease the concentration of Y4-. On the other hand, Increasing the pH of the solution will cause tendency to form slightly soluble metallic hydroxides owing to the reaction below:
(MY)(n-4)+ + nOH- ⇌M(OH)n + Y4-
The extent of hydrolysis (meaning the splitting of water in a reaction such as)
-OAc + H2O ⇌ HOAc + OH-
of (MY)(n-4) depends upon the characteristic of the metal ion and is largely controlled by the solubility product of the metallic hydroxide and the stabiltity constant of the complex. The larger the stability constant of the complex, the lesser the tendency of the metal hydroxide to form.
- The effect of other complexing agents
If another complexing agent (other than Y4-) is also present in the solution, then the concentration of Mn+ in solution will be reduced owing to its ability to further complex with the interfering complexing agent. The relative proportions of the complexes will be dependent on the stability constants of the two types of metal- complexing agent complexes.
EDTA titration has been traditionally used in quantitating calcium ions in water, in a process referred to as determining water hardness. Water hardness is customarily referred to as concentration of calcium in the form of calcium carbonate.
In the following section, we shall use the Ca2+-EDTA titration to illustrate the method of complexometric titration. In this method, a colorimetric indicator, [these are intensely coloured substances in at least one form (bound or unbound to the metal) and do change colour when the metal-ion analyte binds with it], is used.
The reaction between Ca2+ and EDTA proceeds according to the stoichiometry shown below:
Ca2+ + EDTA4− ⇌ Ca − EDTA2−
with a corresponding equilibrium constant for formation expressed as
\(\
\mathrm { K } _ { \mathrm { f } } \left( \mathrm { Ca } - \mathrm { EDTA } ^ { 2 - } \right) = \frac { \left[ \mathrm { Ca } - \mathrm { EDTA } ^ { 2 - } \right] } { \left[ \mathrm { Ca } ^ { + } \right] \left[ \mathrm { EDTA } ^ { 4 - } \right] }
\)
Note that, whereas the equilibrium constants for acids and bases are often tabulated as dissociation constants, equilibrium constants for complex formation are tabulated as formation constants.
Titration Curves
In the former unit, we learnt that in the titration of a strong acid versus a strong base, a plot of pH against the volume of the solution of the strong base addedyields a point of inflexation at the equivalence point. Similarly, in an EDTAversus metal ion titration, if pM (= -log[Mn+], where Mn+ signifies the metal ionwhose concentration is required) is plotted against the volume of EDTA solutionadded, a point of inflexation occurs at the equivalence point. The general shapeof a titration curve obtained following the titration of 100 mL of a 0.1 mol/L solution of Ca2+ ion with a 0. 1 mol/L Na-EDTA solution at two separate pH conditions is shown below.
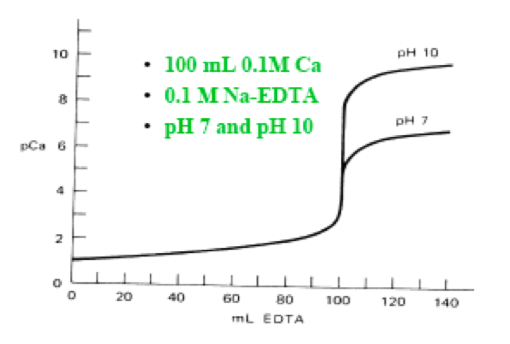
Chemistry of EDTA Titrations
EDTA is used to titrate many ions. For instance, EDTA has been used succesfully over the years for the determination of water hardness (a meassure of the total Ca2+ and Mg2+ ions in water). Water hardness is often conveniently determined by titration of total Ca2+ and Mg2+ ions with EDTA. In this subsection, we shall look at the chemistry of EDTA titrations in general.
In the presence of Eriochrome Black T (EBT) as an indicator, a minor difficultyis usually encountered. Note that metal complexes of EBT are generally red in colour. Therefore, if a colour change is to be observed with EBT indicator, the pH of the solution must be between 7 and 11 so that the blue form of the indicator dominates when the titrant breaks up the red metal-EBT complex at the end point. At a pH of 10, the endpoint reaction is:
MIn- + Y4- + H+ → MY2- + HIn2-
(Red) (Blue)
EDTA is normally standardized against a solution of Ca2+ ions. In the early stages of the EDTA titration with EBT as indicator, the Ca2+-EBT complex does not dissociate appreciably due to a large excess of the untitrated Ca2+ ions in solution (i.e., Ca2+ ions is plenty in solution). As the titration progresses further and more Ca2+ ions is complexed with the titrant, the equilibrium position shifts to the left (i.e., previously complexed Ca-EBT complex, which is red in colour, begins to dissociate to give back more Ca2+ ions for complexation with the titrant EDTA), causing a gradual change in colour from the red Ca-EBT complex.
To avoid this problem of gradual change in colour, a small amount of 1:1 EDTA:Mg is often added to the titration flask (this does not affect the stoichiometry of thetitration reaction because the quantities of EDTA and Mg are equimolar) becauseMgIn complex is sufficiently stable that it will not dissociate appreciably priorto attainement of the equivalence point. (Note that at pH 10, Ca-EDTA complex is more stable than Mg-EDTA complex and also, MgIn-complex is more stable than CaIn-complex.)
Note that when 1:1 EDTA:Mg is added to the Ca2+ analyte-containing indicator solution, the following reactions take place:
MgY2- + Ca2+ → Mg2+ + CaY2- (more stable)
Mg2+ + CaIn- → Ca2+ + MgIn- (more stable)
Explanation:
When EDTA titrant is added, it first binds all the Ca2+ as per the reaction shown below (Note that at pH 10, the predominant species of EDTA is HY3-):
Ca2+ + HY3- → CaY2- + H+
Upto and including the end point, EDTA replaces the less strongly bound Erio-chrome Black T from the Mg2+-EBT complex (represented as MgIn-) as shown below:
MgIn- + HY3- → HIn2- + MgY2-
Types of EDTA Titrations
Important metal ions-EDTA titration experiments fall into the following categories:
A. Direct Titration
In direct titration, the solution containing the metal ion to be determined is buf- fered to the desired pH and titrated directly with a standard EDTA solution. It may be necessary to prevent precipitation of the hydroxide of the metal ion (or a basic salt) by the addition of an auxillary complexing agent (or sometimes calledmasking agent, since they form stable complexes with potential interference), such as tartarate or citrate.
At start (i.e., before addition of titrant):
Mn+ + Ind ⇌ [Mind]n+
where Ind is representing the indicator.
During titration:
Mn+ + [H2Y]2- ⇌ [MY]n-4 + 2H+
where [H2Y]2- is representing EDTA titrant
At Endpoint:
[MInd]n+ + [H2Y]2- ⇌ [MY]n-4 + Ind + 2H+
Note that the complexed ([Mind]n+)and free indicator (ind) have different colours.
At the equivalence point the magnitude of the concentration of the metal ion being determined decreases abruptly. This equivalence point is generally determined by the change in color of a metal indicator that responds to changes in pM.
Titration of 100 mL of a water sample at pH 13 in the presence of acalcium specific indicator such as Eriochrome Black T required 14.0 mL of 0.02M EDTA solution. Calculate the hardness of the water sample as CaCO3 in mg L-1.
Solution
Important infromation to note:
- Molecular weight for CaCO3 is 100g
- The stoichiometry for the reaction between Ca2+ and EDTA at pH 13 is given by:
Ca2+ + EDTA4- ⇌ Ca − EDTA2-
- Both Mg2+ and Ca2+ contribute to water hardness. Both metal ions have the same stoichiometry with EDTA, hence the titration includes the sum of Mg and Ca ions in the water sample.
- The14.0mLof0.02MEDTAcontains (\(\dfrac{14.0\ mL}{1000\ mL/L}\ x\ 0.02\ moles/L\)) = 2.80 x 10-4 moles of EDTA.
- From the above 1:1 stoichiometry, the number of Ca2+ ions present in the 100 mL water sample (equivalent to the combined Ca2+ and Mg2+ ions responsible for water hardness) should be equal to the number of moles of the titrant, EDTA.
- Hence, number of moles of Ca2+ ions present in the 100 mL water sample = 2.80 x 10-4 moles.
- 2.80 x 10-4 moles of Ca2+ is equivalent to (2.80 x 10-4 moles) x 100 g mole-1 CaCO3 =2.80x10-2 g=2.80x10-2 g x 1000mg g-1 =28.0 mg of Ca (as CaCO3).
- Therefore, the hardness of the water is 28.0 mg present in the 100 mL of water \(\ =\dfrac{28.0\ mg}{100\ ml\ /\ 1000\ mlL^{-1}}=280\ mg\ L^{-1} \) hardness.
A 50.00 mL water sample required 21.76 mL of 0.0200 mol/L EDTA to titrate water hardness at pH 13.0. What was the hardness in mg L-1 of CaCO3 ?
- Answer
B. Back titration
This is for the determination of metal ions that cannot be titrated directly with EDTA, say in alkaline solution (e.g., Mn2+ and Al3+) due to precipitation of their hydroxides).
In back titration, an excess known amount of a standard EDTA solution is added to the solution of the analyte. The resulting solution mixture is then buffered to the desired pH, and the excess EDTA titrated with a standard solution of a second metal ion. Examples of metal ions often used as the second metal includesolutions of; ZnCl2, ZnSO4, MgCl2 or MgSO4. The end point is then detected with the aid of an appropriate metal indicator that responds to the second metal ion introduced in the back titration.
The following steps apply:
Mn+ + [H2Y]2- ⇌ [MY]n-4 + 2H+
where [H2Y]2- is representing EDTA titrant
Zn2+ + [H2Y]2- ⇌ [ZnY]-2 + 2H+
At Endpoint:
Zn2+ + ind + ⇌ [Znind]2+
Back titration becomes necessary if analyte:
- precipitates in the absence of EDTA,
- reacts too slowly with EDTA, or
- blocks the indicator.
A 3208 g sample of nickel ore was processed to remove interferences and 50.00 ml of 0.1200 mol L-1 EDTA was added in excess to react with Ni2+ ions in solution. The excess EDTA was titrated with 24.17 mL of 0.0755 mol L-1standard Mg2+. Calculate the %Ni in the ore.
Solution
- The stoichiometry for the reaction between Ni2+ (or Mg2+) and EDTA can be represented as: Ni2+ + EDTA4− ⇌ Ni − EDTA2−
- The stoichiometry represents a 1:1, i.e., for every mole of EDTA present, an equivalent number of moles of Ni2+ is used up.
- Total number of moles of EDTA initially available in the 50.00 mL (=0.050 L) solution of 0.1200 mol L-1 EDTA = (0.1200 moles L-1 x 0.050 L) = 6.0 x 10-3 moles.
- Number of moles of the titrant Mg2+ ions present in the 24.17 mL (= 0.02417 L) of 0.0755 mol L-1 = (0.02417 L x 0.0755 moles L-1) = 1.82 x 10-3 moles
- Therefore, the moles of EDTA that must have reacted with the available Ni2+ ions originally present = (6.0 x 10-3 - 1.82 x 10-3) moles = 4.18 x 10-3 moles.
- Hence, number of moles of Ni2+ ions originally present in the 50.00 mL (= 0.050 L) solution = 4.18 x 10-3 moles.
- This is = 4.18 x 10-3 moles x 58.7g/mol (Atomic weight for Ni = 58.7g) = 0.245366 g
- Therefore, %Ni in the ore \(\ =\dfrac{0.245366\ g}{3208\ g} \) x 100% = 0.00765%
C. Replacement or substitution titration
Substitution titration may be used for the metal ions that do not react (or react unsatisfactorily) with a metal indicator (e.g., Ca2+, Pb2+, Hg2+, Fe3+), or for metal ions that form EDTA complexes that are more stable than those of other metals such as magnesium and calcium.
In this, there is quantitative displacement of the second metal (Mg2+ or Zn2+) from a complex by the analyte metal. Usually, the determination of the metal ions that form weak complexes with the indicator and the colour change is unclear and vague.
The metal cation Mn+ to be determined may be treated with the magnesium complex of EDTA leading to the following reaction:
Mn+ + MgY2- (MY)(n-4)+ + Mg2+
The amount of magnesium ion set free is equivalent to the cation present and can be titrated with a standard solution of EDTA.
The following steps apply:
- Replacement step:
Ca2+ + [MgY]2- ⇌ [CaY]2- + Mg2+
- [Mg Ind]2+ + [H2Y]2- ⇌ [MgY]2- + Ind + 2H+
D. Alkalimetric Titration
When a solution of Na2H2Y is added to a solution containing metallic ions, com- plexes are formed with the liberation of two equivalents of hydrogen ion, i.e.,
Mn+ + H2Y2− ⇌ (MY)(n-4) + 2H+
The hydrogen ions thus set free can be titrated with a standard solution of sodium hydroxide using an acid-base indicator or potentiometric end point. Alternatively, an iodateiodide mixture is added as well as the EDTA solution and the librated iodine is titrated with a standard thiosulphate solution.
Note that the solution of the metal to be determined must be accurately neutralized before titration; this is often a difficult matter on account of the hydrolysisof many salts, and constitutes a weak feature of alkalimetric titration.
A 10.00 mL solution of FeSO4 was added to 50.00 mL of 0.05 mol L-1 Na2H2Y. The H+ released required 18.03 mL of 0.080 mol L-1 NaOH for titration. What was the molar concentration of the FeSO4 solution?
Solution
- The stoichiometry for the reaction between Fe2+ and Na2H2Y can be represented as: Fe2+ + Na2H2Y ⇌ Na2FeY + 2H+. Here 1 mole of Fe2+ ions yields 2 moles of H+ ions.
- The stoichiometry for the acid-base neutralization reaction between the released H+ ions and NaOH in the titration process can be represented as:
H+ + OH− ⇌ H2O . This is 1:1 reaction (i.e., for every 1 mole of H+ ions released, an equivalent moles of hydroxide is needed for neutralization.
- Therefore, number of moles of H+ released = number of moles of OH- ions present in the 18.03 mL (= 0.01803 L) of the 0.080 mol L-1 NaOH solution = 0.01803 L x 0.080 mol L-1 = 1.4424 x 10-3 moles.
- Since for every mole of Fe2+ ions consumed, twice as many moles of H+ ions are released, then the number of moles of Fe2+ ions consumed = \(\ \dfrac{1}{2}\) x 1.4424x10-3 moles = 7.212×10-4 moles
- Therefore, 7.212 x 10-4 moles of Fe2+ ions were present in the original 10.00 mL (= 0.010 L) solution of FeSO4. Thus, Molar concentration of the FeSO4 solution \(\ \dfrac{7.212 x 10^{-4}\ moles}{0.0100\ L}\) = 0.07212 M