Oxidation States (Oxidation Numbers)
- Page ID
- 3660
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Oxidation states simplify the process of determining what is being oxidized and what is being reduced in redox reactions. However, for the purposes of this introduction, it would be useful to review and be familiar with the following concepts:
- oxidation and reduction in terms of electron transfer
- electron-half-equations
To illustrate this concept, consider the element vanadium, which forms a number of different ions (e.g., \(\ce{V^{2+}}\) and \(\ce{V^{3+}}\)). The 2+ ion will be formed from vanadium metal by oxidizing the metal and removing two electrons:
\[ \ce{V \rightarrow V^{2+} + 2e^{-}} \label{1}\]
The vanadium in the \( \ce{V^{2+}}\) ion has an oxidation state of +2. Removal of another electron gives the \(\ce{V^{3+}}\) ion:
\[ \ce{V^{2+} \rightarrow V^{3+} + e^{-}} \label{2}\]
The vanadium in the \(\ce{V^{3+} }\) ion has an oxidation state of +3. Removal of another electron forms the ion \(\ce{VO2+}\):
\[ \ce{V^{3+} + H_2O \rightarrow VO^{2+} + 2H^{+} + e^{-}} \label{3}\]
The vanadium in the \(\ce{VO^{2+}}\) is now in an oxidation state of +4.
Notice that the oxidation state is not always the same as the charge on the ion (true for the products in Equations \ref{1} and \ref{2}), but not for the ion in Equation \ref{3}).
The positive oxidation state is the total number of electrons removed from the elemental state. It is possible to remove a fifth electron to form another the \(\ce{VO_2^{+}}\) ion with the vanadium in a +5 oxidation state.
\[ \ce{VO^{2+} + H_2O \rightarrow VO_2^{+} + 2H^{+} + e^{-}}\]
Each time the vanadium is oxidized (and loses another electron), its oxidation state increases by 1. If the process is reversed, or electrons are added, the oxidation state decreases. The ion could be reduced back to elemental vanadium, with an oxidation state of zero.
If electrons are added to an elemental species, its oxidation number becomes negative. This is impossible for vanadium, but is common for nonmetals such as sulfur:
\[ \ce{S + 2e^- \rightarrow S^{2-}} \]
Here the sulfur has an oxidation state of -2.
Summary
The oxidation state of an atom is equal to the total number of electrons which have been removed from an element (producing a positive oxidation state) or added to an element (producing a negative oxidation state) to reach its present state.
- Oxidation involves an increase in oxidation state
- Reduction involves a decrease in oxidation state
Recognizing this simple pattern is the key to understanding the concept of oxidation states. The change in oxidation state of an element during a reaction determines whether it has been oxidized or reduced without the use of electron-half-equations.
Determining oxidation states
Counting the number of electrons transferred is an inefficient and time-consuming way of determining oxidation states. These rules provide a simpler method.
- The oxidation state of an uncombined element is zero. This applies regardless of the structure of the element: Xe, Cl2, S8, and large structures of carbon or silicon each have an oxidation state of zero.
- The sum of the oxidation states of all the atoms or ions in a neutral compound is zero.
- The sum of the oxidation states of all the atoms in an ion is equal to the charge on the ion.
- The more electronegative element in a substance is assigned a negative oxidation state. The less electronegative element is assigned a positive oxidation state. Remember that electronegativity is greatest at the top-right of the periodic table and decreases toward the bottom-left.
- Some elements almost always have the same oxidation states in their compounds:
| Element | Usual oxidation state | Exceptions |
|---|---|---|
| Group 1 metals | Always +1 | |
| Group 2 metals | Always +2 | |
| Oxygen | Usually -2 | Peroxides and F2O (see below) |
| Hydrogen | Usually +1 | Metal hydrides (-1) (see below) |
| Fluorine | Always -1 | |
| Chlorine | usually -1 | Compounds with O or F (see below) |
The reasons for the exceptions
Hydrogen in the metal hydrides: Metal hydrides include compounds like sodium hydride, NaH. Here the hydrogen exists as a hydride ion, H-. The oxidation state of a simple ion like hydride is equal to the charge on the ion—in this case, -1.
Alternatively, the sum of the oxidation states in a neutral compound is zero. Because Group 1 metals always have an oxidation state of +1 in their compounds, it follows that the hydrogen must have an oxidation state of -1 (+1 -1 = 0).
Oxygen in peroxides: Peroxides include hydrogen peroxide, H2O2. This is an electrically neutral compound, so the sum of the oxidation states of the hydrogen and oxygen must be zero.
Because each hydrogen has an oxidation state of +1, each oxygen must have an oxidation state of -1 to balance it.
Oxygen in F2O: The deviation here stems from the fact that oxygen is less electronegative than fluorine; the fluorine takes priority with an oxidation state of -1. Because the compound is neutral, the oxygen has an oxidation state of +2.
Chlorine in compounds with fluorine or oxygen: Because chlorine adopts such a wide variety of oxidation states in these compounds, it is safer to simply remember that its oxidation state is not -1, and work the correct state out using fluorine or oxygen as a reference. An example of this situation is given below.
What is the oxidation state of chromium in Cr2+?
Solution
For a simple ion such as this, the oxidation state equals the charge on the ion: +2 (by convention, the + sign is always included to avoid confusion)
What is the oxidation state of chromium in CrCl3?
This is a neutral compound, so the sum of the oxidation states is zero. Chlorine has an oxidation state of -1 (no fluorine or oxygen atoms are present). Let n equal the oxidation state of chromium:
n + 3(-1) = 0
n = +3
The oxidation state of chromium is +3.
What is the oxidation state of chromium in Cr(H2O)63+?
Solution
This is an ion and so the sum of the oxidation states is equal to the charge on the ion. There is a short-cut for working out oxidation states in complex ions like this where the metal atom is surrounded by electrically neutral molecules like water or ammonia.
The sum of the oxidation states in the attached neutral molecule must be zero. That means that you can ignore them when you do the sum. This would be essentially the same as an unattached chromium ion, Cr3+. The oxidation state is +3.
What is the oxidation state of chromium in the dichromate ion, Cr2O72-?
The oxidation state of the oxygen is -2, and the sum of the oxidation states is equal to the charge on the ion. Don't forget that there are 2 chromium atoms present.
2n + 7(-2) = -2
n = +6
What is the oxidation state of copper in CuSO4?
Solution
Unfortunately, it isn't always possible to work out oxidation states by a simple use of the rules above. The problem in this case is that the compound contains two elements (the copper and the sulfur) with variable oxidation states.
In cases like these, some chemical intuition is useful. Here are two ways of approaching this problem:
- Recognize CuSO4 as an ionic compound containing a copper ion and a sulfate ion, SO42-. To form an electrically neutral compound, the copper must be present as a Cu2+ ion. The oxidation state is therefore +2.
- Recognize the formula as being copper(II) sulfate (the (II) designation indicates that copper is in a +2 oxidation state, as discussed below).
Using oxidation states
In naming compounds
You will have come across names like iron(II) sulfate and iron(III) chloride. The (II) and (III) are the oxidation states of the iron in the two compounds: +2 and +3 respectively. That tells you that they contain Fe2+ and Fe3+ ions.
This can also be extended to negative ions. Iron(II) sulfate is FeSO4. The sulfate ion is SO42-. The oxidation state of the sulfur is +6 (work it out!); therefore, the ion is more properly named the sulfate(VI) ion.
The sulfite ion is SO32-. The oxidation state of the sulfur is +4. This ion is more properly named the sulfate(IV) ion. The -ate ending indicates that the sulfur is in a negative ion.
FeSO4 is properly named iron(II) sulfate(VI), and FeSO3 is iron(II) sulfate(IV). Because of the potential for confusion in these names, the older names of sulfate and sulfite are more commonly used in introductory chemistry courses.
Using oxidation states to identify what has been oxidized and what has been reduced
This is the most common function of oxidation states. Remember:
- Oxidation involves an increase in oxidation state
- Reduction involves a decrease in oxidation state
In each of the following examples, we have to decide whether the reaction is a redox reaction, and if so, which species have been oxidized and which have been reduced.
This is the reaction between magnesium and hydrogen chloride:
\[ \ce{Mg + 2HCl -> MgCl2 +H2} \nonumber\]
Solution
Assign each element its oxidation state to determine if any change states over the course of the reaction:
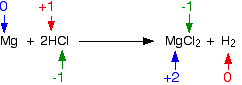
The oxidation state of magnesium has increased from 0 to +2; the element has been oxidized. The oxidation state of hydrogen has decreased—hydrogen has been reduced. The chlorine is in the same oxidation state on both sides of the equation—it has not been oxidized or reduced.
The reaction between sodium hydroxide and hydrochloric acid is:
\[ NaOH + HCl \rightarrow NaCl + H_2O\]
The oxidation states are assigned:
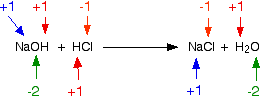
None of the elements are oxidized or reduced. This is not a redox reaction.
The reaction between chlorine and cold dilute sodium hydroxide solution is given below:
\[ \ce{2NaOH + Cl_2 \rightarrow NaCl + NaClO + H_2O} \nonumber\]
It is probable that the elemental chlorine has changed oxidation state because it has formed two ionic compounds. Checking all the oxidation states verifies this:
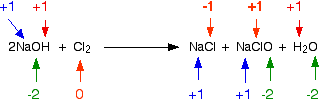
Chlorine is the only element to have changed oxidation state. However, its transition is more complicated than previously-discussed examples: it is both oxidized and reduced. The NaCl chlorine atom is reduced to a -1 oxidation state; the NaClO chlorine atom is oxidized to a state of +1. This type of reaction, in which a single substance is both oxidized and reduced, is called a disproportionation reaction.
Using oxidation states to determine reaction stoichiometry
Oxidation states can be useful in working out the stoichiometry for titration reactions when there is insufficient information to work out the complete ionic equation. Each time an oxidation state changes by one unit, one electron has been transferred. If the oxidation state of one substance in a reaction decreases by 2, it has gained 2 electrons.
Another species in the reaction must have lost those electrons. Any oxidation state decrease in one substance must be accompanied by an equal oxidation state increase in another.
Ions containing cerium in the +4 oxidation state are oxidizing agents, capable of oxidizing molybdenum from the +2 to the +6 oxidation state (from Mo2+ to MoO42-). Cerium is reduced to the +3 oxidation state (Ce3+) in the process. What are the reacting proportions?
Solution
The oxidation state of the molybdenum increases by 4. Therefore, the oxidation state of the cerium must decrease by 4 to compensate. However, the oxidation state of cerium only decreases from +4 to +3 for a decrease of 1. Therefore, there must be 4 cerium ions involved for each molybdenum ion; this fulfills the stoichiometric requirements of the reaction.
The reacting proportions are 4 cerium-containing ions to 1 molybdenum ion.
Here is a more common example involving iron(II) ions and manganate(VII) ions:
A solution of potassium manganate(VII), KMnO4, acidified with dilute sulfuric acid oxidizes iron(II) ions to iron(III) ions. In the process, the manganate(VII) ions are reduced to manganese(II) ions. Use oxidation states to work out the equation for the reaction.
The oxidation state of the manganese in the manganate(VII) ion is +7, as indicated by the name (but it should be fairly straightforward and useful practice to figure it out from the chemical formula)
In the process of transitioning to manganese(II) ions, the oxidation state of manganese decreases by 5. Every reactive iron(II) ion increases its oxidation state by 1. Therefore, there must be five iron(II) ions reacting for every one manganate(VII) ion.
The left-hand side of the equation is therefore written as: MnO4- + 5Fe2+ + ?
The right-hand side is written as: Mn2+ + 5Fe3+ + ?
The remaining atoms and the charges must be balanced using some intuitive guessing. In this case, it is probable that the oxygen will end up in water, which must be balanced with hydrogen. It has been specified that this reaction takes place under acidic conditions, providing plenty of hydrogen ions.
The fully balanced equation is displayed below:
\[ MnO_4^- + 8H^+ + 5Fe^{2+} \rightarrow Mn^{2+} + 4H_2O + 5Fe^{3+} \nonumber\]
Contributors and Attributions
Jim Clark (Chemguide.co.uk)


