Distillation

Distillation is an important commercial process that is used in the purification of a large variety of materials. However, before we begin a discussion of distillation, it would probably be beneficial to define the terms that describe the process and related properties. Many of these are terms that you are familiar with but the exact definitions may not be known to you. Let us begin by describing the process by which a substance is transformed from the condensed phase to the gas phase. For a liquid, this process is called vaporization and for a solid it is called sublimation. Both processes require heat. This is why even on a hot day at the beach, if there is a strong breeze blowing, it may feel cool or cold after you come out of the water. The wind facilitates the evaporation process and you supply some of the heat that is required. All substances regardless of whether they are liquids or solids are characterized by a vapor pressure. The vapor pressure of a pure substance is the pressure exerted by the substance against the external pressure which is usually atmospheric pressure. Vapor pressure is a measure of the tendency of a condensed substance to escape the condensed phase. The larger the vapor pressure, the greater the tendency to escape. When the vapor pressure of a liquid substance reaches the external pressure, the substance is observed to boil. If the external pressure is atmospheric pressure, the temperature at which a pure substance boils is called the normal boiling point. Solid substances are not characterized by a similar phenomena as boiling. They simply vaporize directly into the atmosphere. Many of you may have noticed that even on a day in which the temperature stays below freezing, the volume of snow and ice will appear to decrease, particularly from dark pavements on the streets. This is a consequence of the process of sublimation. Both vaporization and sublimation are processes that can be used to purify compounds. In order to understand how to take advantage of these processes in purifying organic materials, we first need to learn how pure compounds behave when they are vaporized or sublimed.

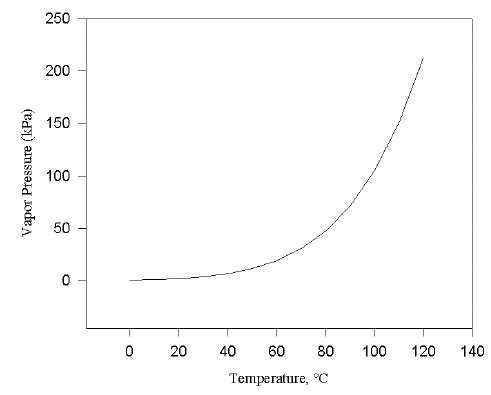
Figure 1. Vapor pressure dependence on temperature for water.

Let's begin by discussing the vapor pressure of a pure substance and how it varies with temperature. Vapor pressure is an equilibrium property. If we return to that hot windy day at the beach and consider the relative humidity in the air, the cooling effect of the wind would be most effective if the relative humidity was low. If the air contained a great deal of water vapor, its cooling effect would be greatly diminished and if the relative humidity was 100%, there would be no cooling effect. Everyone in St. Louis has experienced how long it takes to dry off on a hot humid day. At equilibrium, the process of vaporization is compensated by an equal amount of condensation. Incidentally, if vaporization is an endothermic process (i.e. heat is absorbed), condensation must be an exothermic process (i.e. heat is liberated). Now consider how vapor pressure varies with temperature. Figure 1 illustrates that vapor pressure is a very sensitive function of temperature. It does not increase linearly but in fact increases exponentially with temperature. A useful "rule of thumb" is that the vapor pressure of a substance roughly doubles for every increase in 10 °C. If we follow the temperature dependence of vapor pressure for a substance like water left out in an open container, we would find that the equilibrium vapor pressure of water would increase until it reached 1 atmosphere or 101325 Pa (101.3 kPa, 760 mm Hg). At this temperature and pressure, the water would begin to boil and would continue to do so until all of the water distilled or boiled off. It is not possible to achieve a vapor pressure greater than 1 atmosphere in a container left open to the atmosphere. Of course, if we put a lid on the container, the vapor pressure of water or any other substance for that matter would continue to rise with temperature until the container ruptured. Elevation of the boiling point with increase in external pressure is the principle behind the use of a pressure cooker.

Vacuum Distillation

Elevation of the boiling point with an increase in external pressure, while important in cooking and sterilizing food or utensils, is less important in distillation. However, it illustrates an important principle that is used in the distillation of many materials. If the boiling point of water is increased when the external pressure is increased, then decreasing the external pressure should decrease the boiling point. While this is not particularly important for the purification of water, this principle is used in the process of freeze drying, an important commercial process. In addition, many compounds cannot be distilled at atmospheric pressure because their boiling points are so high. At their normal boiling points, the compounds decompose. Some of these materials can be distilled under reduced pressure however, because the required temperature to boil the substance can be lowered significantly. Rewording the "rule of thumb" described above so that it is applicable here suggests that the boiling point will be lowered by 10 °C each time the external pressure is halved. For example, if the external pressure above a substance is reduced to 1/16 of an atmosphere by mean of a mechanical pump, the boiling point will have been reduced four times by 10 °C for a total reduction of 40 °C (1 atm x (1/2)(1/2)(1/2)(1/2) =1/16 atm).

Figure 2. A nomograph used to estimate boiling points at reduced pressures. To use, place a straight edge on two of the three known properties and read out the third. Column c is in mm of mercury. An atmosphere is also equivalent to 101.3 kPa and will support a column of mercury, 76 cm (760 mm).

A nomograph is a useful device that can be used to estimate the boiling point of a liquid under reduced pressure under any conditions provide either the normal boiling point or the boiling point at a some given pressure is available. To use the nomograph given the normal boiling point, simply place a straight edge at on the temperature in the central column of the nomograph (b). Rotating the straight edge about this temperature will afford the expected boiling point for any number of external pressures. Simply read the temperature and the corresponding pressure from where the straight edge intersects the first and third columns. As an example lets choose a normal boiling point of 400 °C. Using the nomograph in Figure 2 and this temperature for reference, rotating the straight edge about this temperature will afford a continuous range of expected boiling points and the required external pressures necessary to achieve the desired boiling point. At a pressure of 6 mm, the expected boiling point would be 200 °C. Likewise, our compound boiling at 400 °C at 1 atm would be expected to boil at 145 °C at 0.1 mm external pressure.

Simple Distillation

Although all of us have brought water to a boil many times, some of us may have not realized that the temperature of pure boiling water does not change as it distills. This is why vigorous boiling does not cook food any faster than a slow gentle boil. The observation that the boiling point of a pure material does not change during the course of distillation is an important property of a pure material. The boiling point and boiling point range have been used as criteria in confirming both the identity and purity of a substance. For example, if we synthesized a known liquid that boiled at 120-122 °C, this value could be used to confirm that we prepared what we were interested in and that our substance was reasonably pure. Of course, additional criteria must also be satisfied before the identity and purity of the liquid are known with certainty. In general, a boiling point range of 1-2 °C is usually taken as an indication of a pure material. You will use both of these properties later in the semester to identity an unknown liquid.

Occasionally, mixtures of liquids called azeotropes can be encountered that mimic the boiling behavior of pure liquids. These mixtures when present at specific concentrations usually distill at a constant boiling temperature and can not be separated by distillation. Examples of such mixtures inlcude:

• 95% ethanol-5% water (bp 78.1 °C)
• 20% acetone-80% chloroform (bp 64.7 °C)
• 74.1% benzene, 7.4% water, 18.5 % ethanol (bp 64.9)

The azeotropic composition sometimes boils lower the than boiling point of its components and sometimes higher. Mixtures of these substances at compositions other than those given above behave as mixtures.

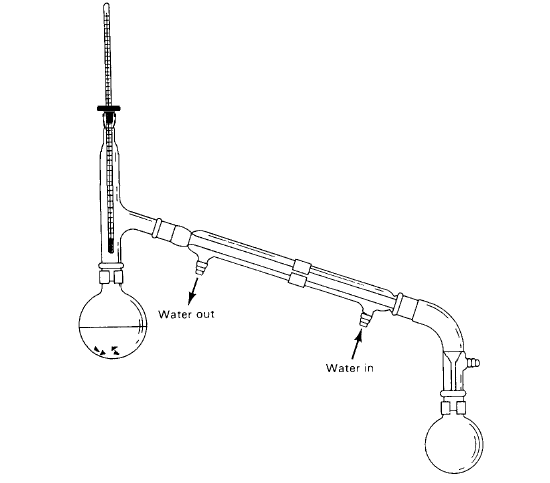
Figure 3. The apparatus used in a simple distillation. Note the position of the thermometer bulb in the distillation head and the arrangement of the flow of the cooling water.

Returning to our discussion of boiling water, if we were making a syrup by the addition of sugar to boiling water, we would find that the boiling point of the syrup would increase as the syrup begins to thicken and the sugar concentration becomes significant. Unlike pure materials, the boiling point of an impure liquid will change and this change is a reflection of the change in the composition of the liquid. In fact it is this dependence of boiling point on composition that forms the basis of using distillation for purifying liquids. We will begin our discussion of distillation by introducing Raoult's Law, which treats liquids in a simple and ideal, but extremely useful manner.

\[ P_a^{obs} = \chi P_A^{o} \label{1}\]

where

• \(P_A^{obs}\) is the observed vapor pressure of A 1
• \(\chi = \dfrac{n_A}{n_A + n_B + n_C +...}\)
• \(P_A^{o}\) = vapor pressure of pure A
• nA, nB, nC ... : number of moles of A, B, C, ...

This relationship as defined is capable of describing the boiling point behavior of compound A in a mixture of compounds under a variety of different circumstances. Although this equation treats mixtures of compounds in an oversimplified fashion and is not applicable to azeotropic compositions, it does give a good representation of the behavior of many mixtures.

Let's first consider a binary system (2 components) in which only one of the two components is appreciably volatile. Our previous discussion of sugar + water is a good example. Raoult's law states that the observed vapor pressure of water is simply equal to the product of the mole fraction of the water present and the vapor pressure of pure water at the temperature of the mixture. Once the sugar-water mixture starts to boil, and continues to boil, we know that the observed vapor pressure of the water must equal one atmosphere. Water is the only component that is distilling. Since the mole fraction of water in a mixture of sugar-water must be less than 1, in order for the observed vapor pressure of water (\(P_A^{o}\)) to equal one atmosphere, \(P_A^{o}\) must be greater than one atmosphere. This can only happen according to Figure 1 if the temperature of the mixture is greater than 100 °C. As the distillation of water continues, the mole fraction of the water continues to decrease thereby causing the temperature of the mixture to increase. Remember, heat is constantly being added. If at some point the composition of the solution becomes saturated with regards to sugar and the sugar begins to crystallize out of solution, the composition of the solution will become constant; removal of any additional water will simply result in the deposit of more sugar crystals. Under these set of circumstances, the composition of the solution will remain constant and so will the temperature of the solution although it will exceed 100 °C.

During the course of the distillation, the water vapor which distilled was initially at the temperature of the solution. Suspending a thermometer above this solution will record the temperature of the escaping vapor. As it departs from the solution, the temperature of the vapor will cool by collisions with the surface of vessel until it reaches 100 °C. Cooling below this temperature will cause most of the vapor to condense to a liquid. If cooling to 20 °C occurs in the condenser of a distillation apparatus, then by using the appropriate geometry as shown in Figure 3, it would be possible to collect nearly all of the liquid. The only vapor that would be lost to the environment would be that small amount associated with the vapor pressure of water at 20 °C. Since the vapor pressure of water at 20 °C is roughly 2.3 kPa, then 2.3/101.325 or 0.023 would be the fraction of water that would not condense and would pass out of the condenser. This is why the distillate is frequently chilled in an ice bath during the distillation.

The distillation of a volatile material from non-volatile is one practical use of distillation which works very well. However, often there may be other components present that although they may differ in relative volatility, are nevertheless volatile themselves. Let's now consider the two component system you will be using in the distillations you will perform in the laboratory, cyclohexane and methylcyclohexane. The vapor pressures of these two materials in pure form are given in Table 1. As you can see from this table, although cyclohexane is more volatile than methylcyclohexane, the difference in volatility between the two at a given temperature is not very great. This means that both materials will contribute substantially to the total vapor pressure exhibited by the solution if the distillation is carried out at 1 atmosphere. The total pressure, \(P_T\), exerted by the solution against the atmosphere according to Dalton's Law of partial pressures, Equation \(\ref{2}\), is simply the sum of the observed vapor pressures of cyclohexane, \(P_c^{obs}\), and methylcyclohexane, \(P_m^{obs}\) :

\[P_T = P_c^{obs} + P^{obs}_m \label{2}\]

As before, boiling will occur when the total pressure, \(P_T\) , equals an atmosphere. However since we have two components contributing to the total pressure, we need to determine the relative contributions of each. Again we can use Raoult's Law, but we need more information about the system before we can do so. In particular we need to know the composition of the solution of cyclohexane and methylcyclohexane. For ease of calculation, let's assume that our original solution has equal molar amounts of the two components. What we would like to determine is whether it would be possible to separate cyclohexane from methylcyclohexane by distillation. By separation, we would like to determine if it would be possible to end up with two receiver flasks at the end of the experiment that would contain mainly cyclohexane in one and mainly methylcyclohexane in the other. It is clear that at some point we will need to intervene in this experiment. Otherwise, if we were to collect the entire contents of the original distilling flask, called the pot, into one receiver flask, we would end up with the same composition as we started. Initially the mole fractions of both cyclohexane and methylcyclohexane are 0.5. From Raoult's Law (Equation \(\ref{1}\)), Dalton's Law (Equation \(\ref{2}\)) and the information in Table 1, we can estimate that boiling will occur at approximately 362 K when the total pressure of the two components equals one atmosphere or 101.3 kPa.:

\[P_T = P_c^{obs} + P_m^{obs} = 0.5(128.5\, kPa) + 0.5(71.1\, kPa) » 101.3\, kPa\]

The first thing that we should note is that the initial boiling point is higher than the lowest boiling component and lower than the highest boiling component. Next, we should inquire about the composition of the vapor. Is the composition of the vapor the same as the initial composition of the pot or is it enriched in the more volatile component? If the composition of the vapor is the same as that of the original mixture, then distillation will not be successful in separating the two components. However, we should ask, "What is the composition of the vapor?" Before the vapor is cooled and condenses on the condenser, we can treat the vapor as an ideal gas. Recalling that: PV = nRT, where P is the pressure of the gas or vapor, V is the volume it occupies, n is the number of moles of gas, R is the Gas Constant (0.0821 L. atm.K^-1.mol^-1) and T is the temperature, we can determine the composition of the vapor by taking advantage of the following factors. First we note that:

\[P_TV = nTRT\]

so that

\[P_c^{obs}V = ncRT\]

and

\[P_m^{obs}V = nmRT\]

where nT refers to the total number of moles, since

\[(P_c^{obs} + P_m^{obs}) = (n_c + n_m)RT.\]

If the total vapor can be treated as an ideal gas, then according to Dalton's Law, so can each of the components. Since the two components are in thermal contact and are distilling together, we can expect them to be at the same temperature. We don't necessarily know the volume of the container, but since it is assumed that the volumes of the molecules are very small in comparison to the total volume the gas occupies, whatever the value of \(V\), it is the same for both components. This means we can establish the following ratio:

\[ \dfrac{P_c^{obs}}{ P^{obs}_m} = \dfrac{nc}{nm}\]

which in turn allows us to determine the composition of the vapor from the observed partial pressures of the two components. If we use the experimental values found in Table 1, we conclude that the composition of the vapor is 1.8/1, and is indeed enriched in the more volatile component.

Table 1. Vapor pressures of cyclohexane and methyl cyclohexane as a function of temperature.

Temperature (K)	Vapor Pressure (kPa)	Temperature (K)		Vapor Pressure (kPa)
cyclohexane		methylcyclohexane
300	14.1	300		6.7
305	17.6	305		8.5
310	21.7	310		10.6
315	26.5	315		13.2
320	32.2	320		16.2
325	38.8	325		19.8
330	46.5	330		24.0
335	55.3	335		28.9
340	65.4	340		34.6
345	77.0	345		41.2
350	90.0	350		48.7
354	101.3	354		55.4
360	121.3	360		66.9
362	128.5	362		71.1
365	139.9	365		77.9
370	160.5	370		90.2
373	174.0	373		101.3
380	208.8	380		119.3
385	236.7	385		136.4
390	267.3	390		155.3
395	300.9	395		176.2
400	337.5	400		199.1

This simple treatment allows us to understand the principles behind distillation. However it is important to point out that distillation is far more complex than our simple calculation indicates. For example, we just calculated the composition of the vapor as soon as the solution begins to boil and we have correctly determined that the vapor will be enriched in the more volatile component. This means that as the distillation proceeds, the pot will be enriched in the less volatile component. Since the composition of the pot will change from the initial 1:1 mole ratio and become enriched in the less volatile component; the new composition in the pot will introduce changes in the composition of the vapor. The composition of the vapor will also change from the initial ratio we just calculated to a new ratio to reflect the new composition of the pot. The consequences of these changes are that the temperature of both the pot and the distillate will slowly increase from the initial value to a value approaching the boiling point and composition of the less volatile component. If we are interested in separating our mixture into components, we are left with the task of deciding how much material to collect in each receiver and how many receivers to use. Obviously this will depend on the quality of separation we are interested in achieving. Generally, the more receivers we use, the less material we will have in each. It is possible to combine fractions that differ very little in composition but this requires us to analyze each mixture. While it is possible to do this, in general, we really want to end with three receivers, one each enriched in the two components of our mixture and a third that contains a composition close to the initial composition.

It is difficult to describe how much material to collect in each receiver since the volume collected will depend on the differences in the boiling points of the components. As a general rule, the receiver should be changed for every 10 °C change in boiling point. Each fraction collected can be analyzed and those with compositions similar to the initial composition can be combined. The main fractions collected can then be fractionated a second time if necessary.

The experiment we have just discussed is called a simple distillation. It is an experiment that involves a single equilibration between the liquid and vapor. This distillation is referred to as involving one theoretical plate. As you will see, it is possible to design more efficient distillation columns that provide separations on the basis of many theoretical plates. Before discussing these columns and the advantages offered by such fractionating columns, it is important to understand the basis of the advantages offered by columns with many theoretical plates. The following is a simplified discussion of the process just described involving a column with more than one theoretical plate.

Fractional Distillation

We have just seen that starting with a composition of 1:1, cyclohexane: methylcyclohexane, the composition of the vapor was enriched in the more volatile component. Suppose we were to collect and condense the vapor and then allow the resulting liquid to reach equilibrium with its vapor. Let’s call this liquid, liquid 2. The properties of liquid 2 will differ from the original composition in two ways. First, since the composition of liquid 2 is higher in cyclohexane than the initial one; the temperature at which liquid 2 will boil will be lower than before (what is the approximate boiling point of a 1.8/1 mixture of cyclohexane/methylcyclohexane? see Table 1). In addition, the composition of the vapor, vapor 2, in equilibrium with liquid 2 will again be enriched in the more volatile component. This is exactly what happened in the first equilibration (first theoretical plate) and this process will be repeated with each new equilibration. If this process is repeated many times, the vapor will approach the composition of the most volatile component, in this case pure cyclohexane, and the liquid in the pot will begin to approach the composition of the less volatile component, methylcyclohexane. In order for this distillation to be successful, it is important to allow the condensed liquid which is enriched in the less volatile component relative to its vapor, to return to the pot. In a fractional distillation, the best separation is achieved when the system is kept as close to equilibrium as possible. This means that the cyclohexane should be removed from the distillation apparatus very slowly. Most fractional distillation apparati are designed in such a way as to permit control of the amount of distillate that is removed from the system. Initially the apparatus is set up for total reflux, (i.e. all the distillate is returned back to the system). Once the distillation system reaches equilibrium, a reflux to takeoff ratio of about 100:1 is often used (about 1 out of every 100 drops reaching the condenser is collected in the receiver).

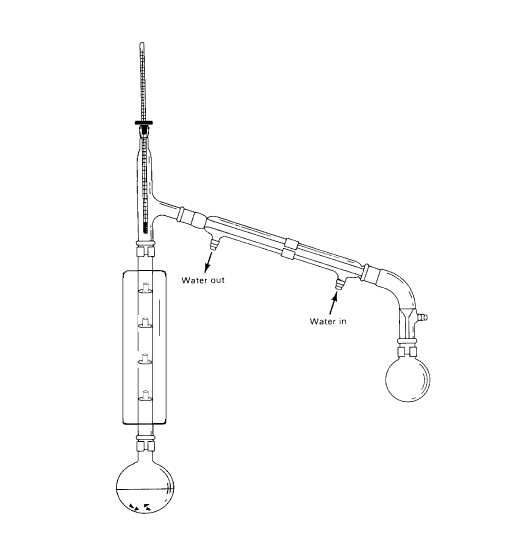
Figure 4. A fractionating column which contains four chambers, each with a center opening into the chamber directly above. The vapor entering the first chamber cools slightly and condenses, filling the lower chamber with liquid. At equilibrium, all chambers are filled with distillate. A portion of the liquid condensing in the first chamber is allowed to return to the pot. The remaining liquid will volatilize and travel up the column condensing in the second chamber and so on. As discussed in the text, the composition of the vapor at each equilibration is enriched in the more volatile component. The heat necessary to volatilize the liquid in each chamber is obtained from the heat released from the condensing vapors replacing the liquid that has been removed. The vacuum jacket that surrounds the column ensures a minimum of heat loss.

A column which allows for multiple equilibrations is called a fractionating column and the process is called fractional distillation. An example of a fractionating column is shown in Figure 4. Each theoretical plate is easy to visualize in this column. The column contains a total of 4 theoretical plates and including the first equilibration between the pot and chamber 1 accounts for a total of 5 from pot to receiver. As you might expect, a problem with this column is the amount of liquid that is retained by the column. Many other column designs have been developed that offer the advantages of multiple theoretical plates with low solvent retention. Typical spinning band columns often used in research laboratories offer fractionating capabilities in the thousand of theoretical plates with solute retention of less than one mL. Commercial distillation columns have been designed for gasoline refineries that are multiple stories high and are capable of separating compounds with boiling points that differ by only a few degrees.

In addition to performing a fractional distillation at one atmosphere pressure, it is also possible to conduct fractional distillations at other pressures. This is often avoided when possible because of the increased difficulty and expense in maintaining the vacuum system leak free.

Steam Distillation

The concentration and isolation of an essential oil from a natural product has had a dramatic impact on the development of medicine and food chemistry. The ability to characterize the structure of the active ingredient from a natural product has permitted synthesis of this material from other chemicals, resulting in a reliable and often cheaper sources of the essential oil. The process often used in this isolation is called steam distillation. Steam distillation is an important technique that has significant commercial applications. Many compounds, both solids and liquids, are separated from otherwise complex mixtures by taking advantage of their volatility in steam. A compound must satisfy three conditions to be successfully separated by steam distillation. It must be stable and relatively insoluble in boiling water, and it must have a vapor pressure in boiling water that is of the order of 1 kPa (0.01) atmosphere. If two or more compounds satisfy these three conditions, they will generally not separate from each other but will be separated from everything else. The following example, expressed as a problem, illustrates the application of steam distillation:

Suppose we have 1 g of an organic compound present in 100 g of plant material composed mainly of macromolecular material such cellulose and related substances. Let's assume that the volatile organic material has a molecular weight of 150 Daltons, a vapor pressure of 1 kPa and is not soluble in water to an appreciable extent. Examples of such materials characterized by these properties include eugenol from cloves, cinnamaldehyde from cinnamon bark or cuminaldehyde from cumin seeds. How much water must we collect to be assured we have isolated all of the natural oil from the bulk of the remaining material?

We can simplify this problem by pointing out that the organic material is not appreciably soluble in water. We know from previous discussions that boiling will occur when the total pressure of our system equals atmospheric pressure. We can also simplify the problem by assuming that the essential oil in not appreciably soluble in the macromolecular material. While in reality this does not have to be correct, this assumption simplifies our calculation. Boiling of our

\[PT = P_{water}^{obs} + P_{org}^{obs}\]

\[PT = \chi_{water} P_{water}^{o} + \chi_{org} P_{org}^{o}\]

mixture will occur close to 100°C. Remember that very little oil is soluble in water which makes the mole fraction of water near unity. Similarly for the our volatile oil, its mole fraction is also close to one according to our assumption. The total pressure, PT, is the sum of the vapor pressure of water, 100 kPa, and the essential oil, \(P_{org}^o\), 1 kPa. Boiling will occur very close to the boiling point of pure water. Treating the water vapor and the organic vapor which are miscible as ideal, the PV ratio for both vapors is given by the following:

\[\dfrac{P_{water}V}{P_{org}V} = \dfrac{n_{water}RT}{n_{org}RT}\]

\[\dfrac{P_{water}}{P_{org}} = \dfrac{n_{water}}{n_{org}}\]

and

\[n_{water} = wt_{water}/18n_{org} = \dfrac{1}{150}\]

rearranging:

\[wt_{water} = \left(\dfrac{100}{1}\right)\left(\dfrac{18}{150}\right) = 120\, g\, water\]

or 120 mL

Our calculation suggests that we can be assured that most of the 1 g of the organic mater has been transferred by the steam if we condense and collect 120 mL of water. The basis of the separation by steam distillation is that while the water and organic condensed phases are immiscible, the vapors of both are miscible. Once condensed, the two separate again allowing for an easy separation. As noted above, both liquids and solids can be distilled by steam.

Contributors and Attributions

• James Chickos, David Garin, and Valerian D'Souza. University of Missouri–St. Louis; Chemistry)