Vapor Pressure
- Page ID
- 3863
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This page looks at how the equilibrium between a liquid (or a solid) and its vapor leads to the idea of a saturated vapor pressure. It also looks at how saturated vapor pressure varies with temperature, and the relationship between saturated vapor pressure and boiling point.
Evaporation: Liquid/Vapor Equilibrium
The average energy of the particles in a liquid is governed by the temperature. The higher the temperature, the higher the average energy. But within that average, some particles have energies higher than the average, and others have energies lower than the average. Some of the more energetic particles on the surface of the liquid can be moving fast enough to escape from the attractive forces holding the liquid together. They evaporate. The diagram shows a small region of a liquid near its surface.
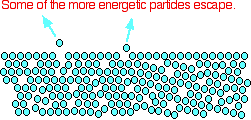
Notice that evaporation only takes place on the surface of the liquid. That's quite different from boiling which happens when there is enough energy to disrupt the attractive forces throughout the liquid. That's why, if you look at boiling water, you see bubbles of gas being formed all the way through the liquid.
If you look at water which is just evaporating in the sun, you don't see any bubbles. Water molecules are simply breaking away from the surface layer. Eventually, the water will all evaporate in this way. The energy which is lost as the particles evaporate is replaced from the surroundings. As the molecules in the water jostle with each other, new molecules will gain enough energy to escape from the surface.
The evaporation of a liquid in a closed container
Now imagine what happens if the liquid is in a closed container. Common sense tells you that water in a sealed bottle does not seem to evaporate - or at least, it does not disappear over time. But there is constant evaporation from the surface. Particles continue to break away from the surface of the liquid - but this time they are trapped in the space above the liquid.
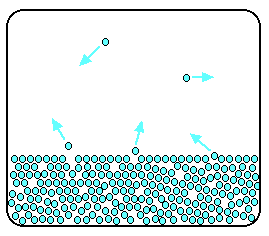
As the gaseous particles bounce around, some of them will hit the surface of the liquid again, and be trapped there. There will rapidly be an equilibrium set up in which the number of particles leaving the surface is exactly balanced by the number rejoining it.

In this equilibrium, there will be a fixed number of the gaseous particles in the space above the liquid. When these particles hit the walls of the container, they exert a pressure. This pressure is called the saturated vapor pressure (also known as saturation vapor pressure) of the liquid.
Measuring the saturated vapor pressure
It is not difficult to show the existence of this saturated vapor pressure (and to measure it) using a simple piece of apparatus. If you have a mercury barometer tube in a trough of mercury, at 1 atmosphere pressure the column will be 760 mm tall. 1 atmosphere is sometimes quoted as 760 mmHg ("millimetres of mercury").
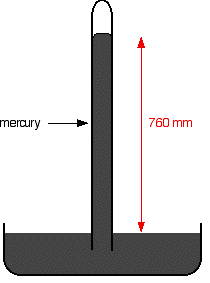
If you squirt a few drops of liquid into the tube, it will rise to form a thin layer floating on top of the mercury. Some of the liquid will evaporate and you will get the equilibrium we've just been talking about - provided there is still some liquid on top of the mercury. It is only an equilibrium if both liquid and vapor are present.
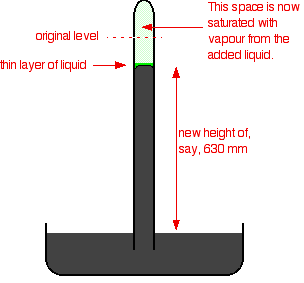
The saturated vapor pressure of the liquid will force the mercury level down a bit. You can measure the drop - and this gives a value for the saturated vapor pressure of the liquid at this temperature. In this case, the mercury has been forced down by a distance of 760 - 630 mm. The saturated vapor pressure of this liquid at the temperature of the experiment is 130 mmHg. You could convert this into proper SI units (pascals) if you wanted to. 760 mmHg is equivalent to 101,325 Pa.
A value of 130 mmHg is quite a high vapor pressure if we are talking about room temperature. Water's saturated vapor pressure is about 20 mmHg at this temperature. A high vapor pressure means that the liquid must be volatile - molecules escape from its surface relatively easily, and aren't very good at sticking back on again either.
That will result in larger numbers of them in the gas state once equilibrium is reached. The liquid in the example must have significantly weaker intermolecular forces than water.
The variation of saturated vapor pressure with temperature
The effect of temperature liquid/ vapor equilibrium
You can look at this in two ways. (1) There is a common sense way. If you increase the temperature, you are increasing the average energy of the particles present. That means that more of them are likely to have enough energy to escape from the surface of the liquid. That will tend to increase the saturated vapor pressure. (2) Or you can look at it in terms of Le Chatelier's Principle - which works just as well in this kind of physical situation as it does in the more familiar chemical examples.
When the space above the liquid is saturated with vapor particles, you have this equilibrium occurring on the surface of the liquid:

The forward change (liquid to vapor) is endothermic. It needs heat to convert the liquid into the vapor. According to Le Chatelier, increasing the temperature of a system in a dynamic equilibrium favors the endothermic change. That means that increasing the temperature increases the amount of vapor present, and so increases the saturated vapor pressure.
The effect of temperature on the saturated vapor pressure of water
The graph shows how the saturated vapor pressure (svp) of water varies from 0°C to 100 °C. The pressure scale (the vertical one) is measured in kilopascals (kPa). 1 atmosphere pressure is 101.325 kPa.
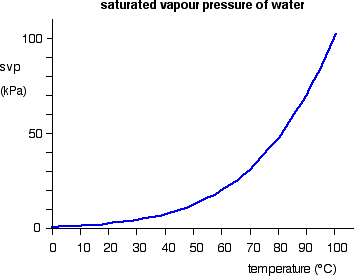
Saturated vapor pressure and boiling point
A liquid boils when its saturated vapor pressure becomes equal to the external pressure on the liquid. When that happens, it enables bubbles of vapor to form throughout the liquid - those are the bubbles you see when a liquid boils.
If the external pressure is higher than the saturated vapor pressure, these bubbles are prevented from forming, and you just get evaporation at the surface of the liquid. If the liquid is in an open container and exposed to normal atmospheric pressure, the liquid boils when its saturated vapor pressure becomes equal to 1 atmosphere (or 101325 Pa or 101.325 kPa or 760 mmHg). This happens with water when the temperature reaches 100°C.
But at different pressures, water will boil at different temperatures. For example, at the top of Mount Everest the pressure is so low that water will boil at about 70°C. Whenever we just talk about "the boiling point" of a liquid, we always assume that it is being measured at exactly 1 atmosphere pressure. In practice, of course, that is rarely exactly true.
Sublimation: solid/vapor Equilibrium
Solids can also lose particles from their surface to form a vapor, except that in this case we call the effect sublimation rather than evaporation. Sublimation is the direct change from solid to vapor (or vice versa) without going through the liquid stage.
In most cases, at ordinary temperatures, the saturated vapor pressures of solids range from low to very, very, very low. The forces of attraction in many solids are too high to allow much loss of particles from the surface. However, there are some which do easily form vapors. For example, naphthalene (used in old-fashioned "moth balls" to deter clothes moths) has quite a strong smell. Molecules must be breaking away from the surface as a vapor, because otherwise you would not be able to smell it. Another fairly common example (discussed in detail on another page) is solid carbon dioxide - "dry ice". This never forms a liquid at atmospheric pressure and always converts directly from solid to vapor. That's why it is known as dry ice.
Contributors and Attributions
Jim Clark (Chemguide.co.uk)


