12.2: General Theory of Column Chromatography
- Page ID
- 5592
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Of the two methods for bringing the stationary phase and the mobile phases into contact, the most important is column chromatography. In this section we develop a general theory that we may apply to any form of column chromatography.
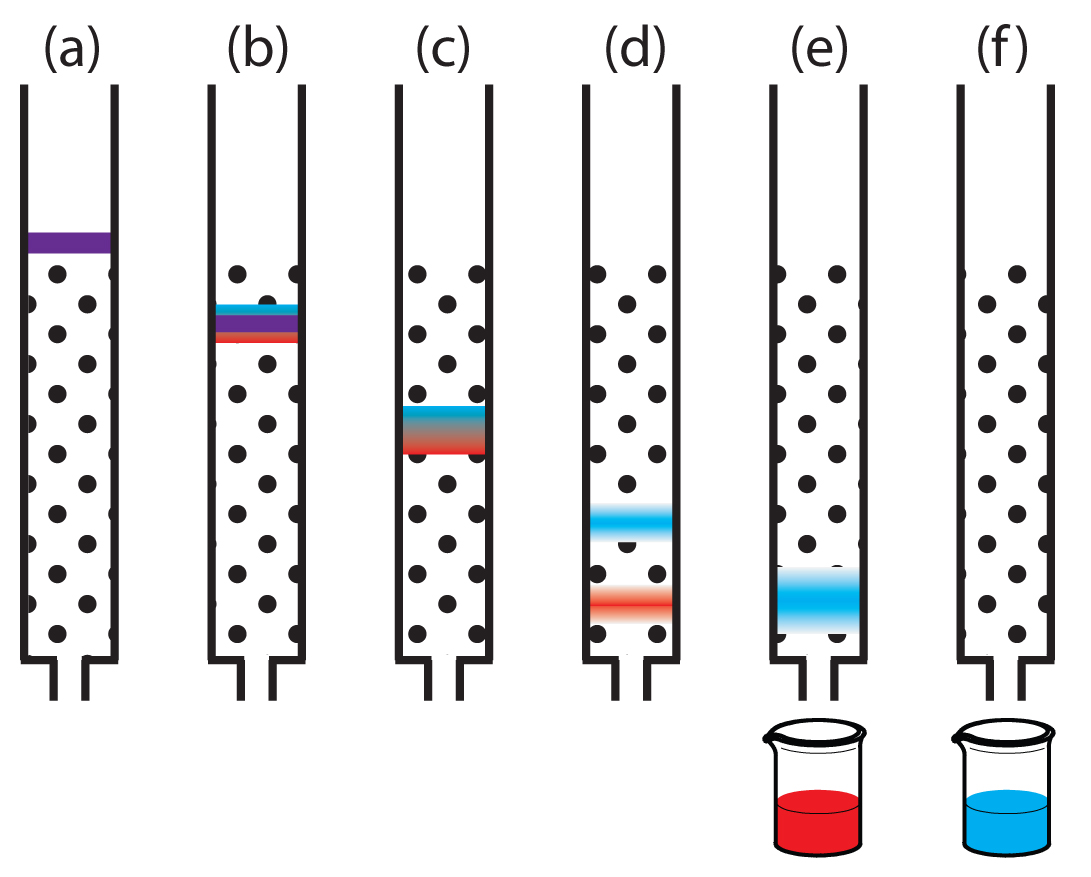
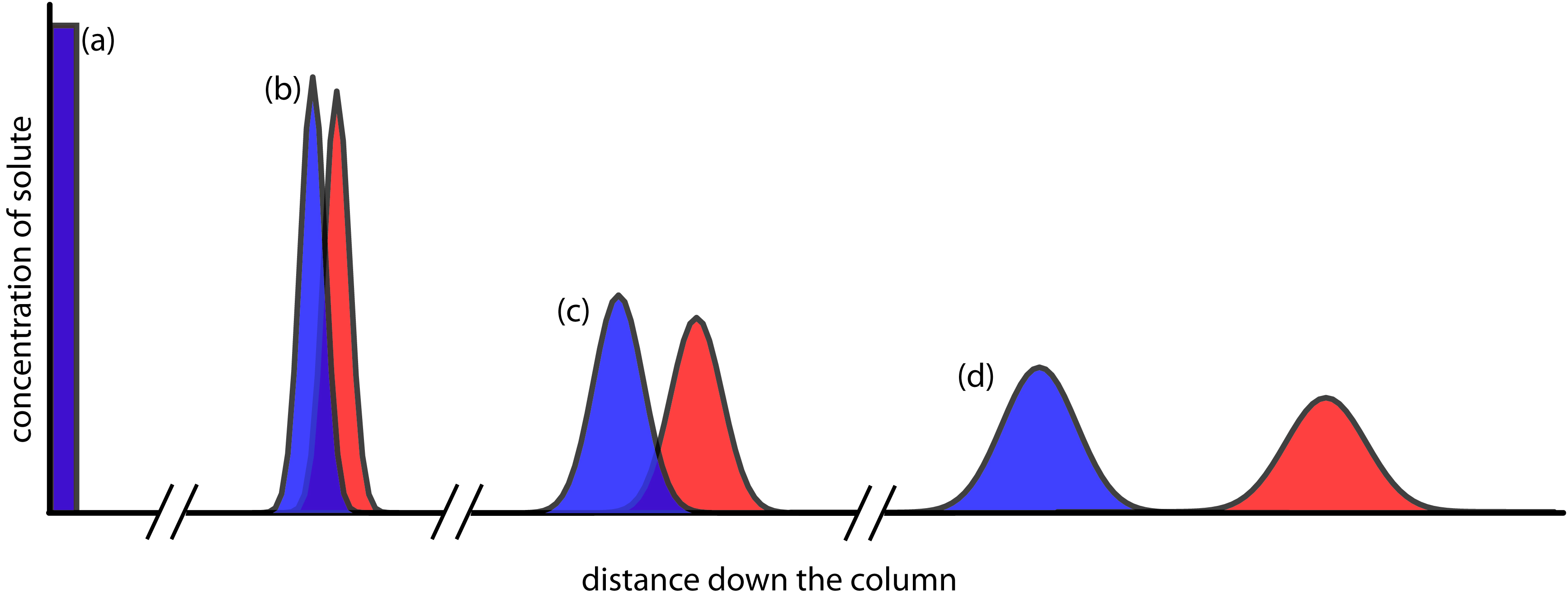
Figure 12.6 provides a simple view of a liquid–solid column chromatography experiment. The sample is introduced at the top of the column as a narrow band. Ideally, the solute’s initial concentration profile is rectangular (Figure 12.7a). As the sample moves down the column the solutes begin to separate (Figures 12.6b,c), and the individual solute bands begin to broaden and develop a Gaussian profile (Figures 12.7b,c). If the strength of each solute’s interaction with the stationary phase is sufficiently different, then the solutes separate into individual bands (Figure 12.6d and Figure 12.7d).
Figure 12.6 Progress of a column chromatographic separation of a two-component mixture. In (a) the sample is layered on top of the stationary phase. As mobile phase passes through the column, the sample separates into two solute bands (b–d). In (e) and (f), we collect each solute as it elutes from the column.
Figure 12.7 An alternative view of the separation in Figure 12.6 showing the concentration of each solute as a function of distance down the column.
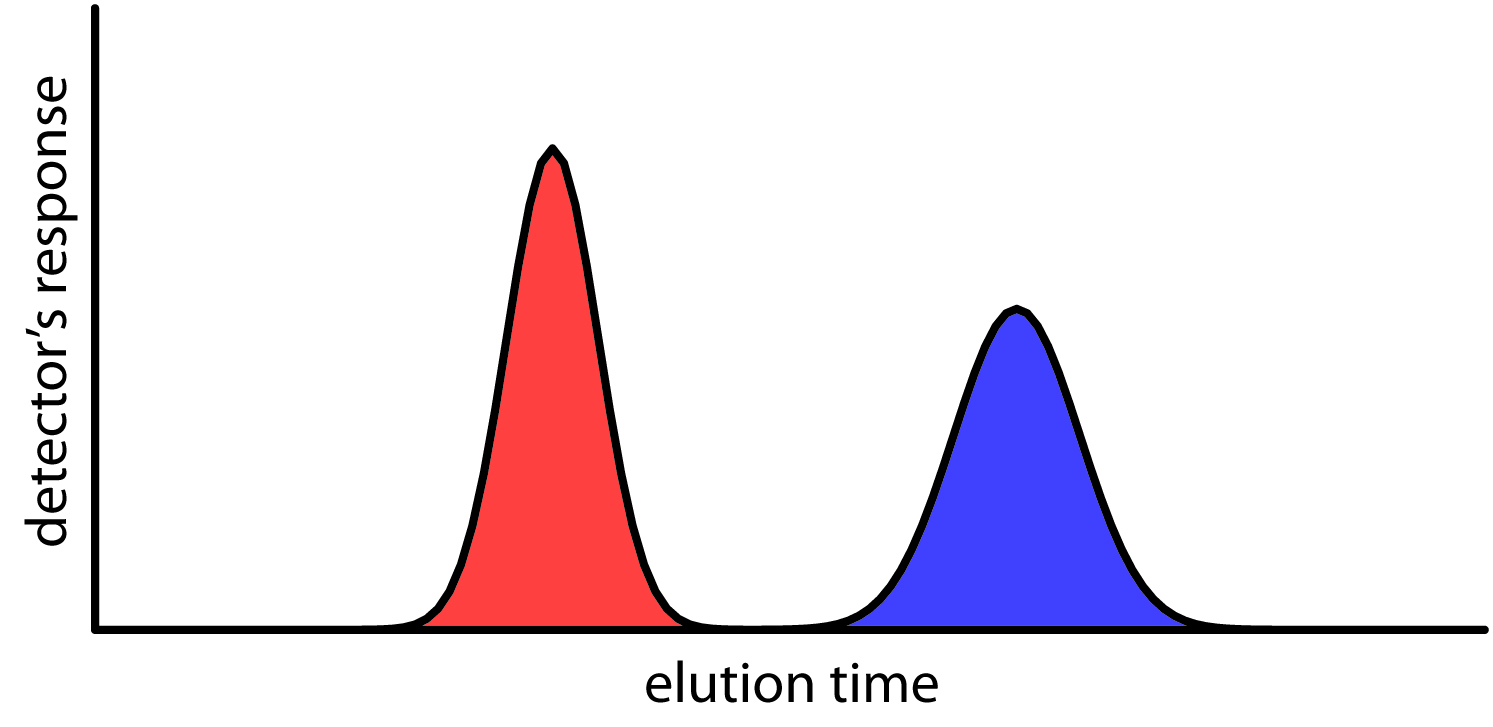
We can follow the progress of the separation either by collecting fractions as they elute from the column (Figure 12.6e,f), or by placing a suitable detector at the end of the column. A plot of the detector’s response as a function of elution time, or as a function of the volume of mobile phase, is known as a chromatogram (Figure 12.8), and consists of a peak for each solute.
Note
There are many possible detectors that we can use to monitor the separation. Later sections of this chapter describe some of the most popular.
Figure 12.8 Chromatogram for the separation shown in Figure 12.6 and Figure 12.7, showing the detector’s response as a function of the elution time.
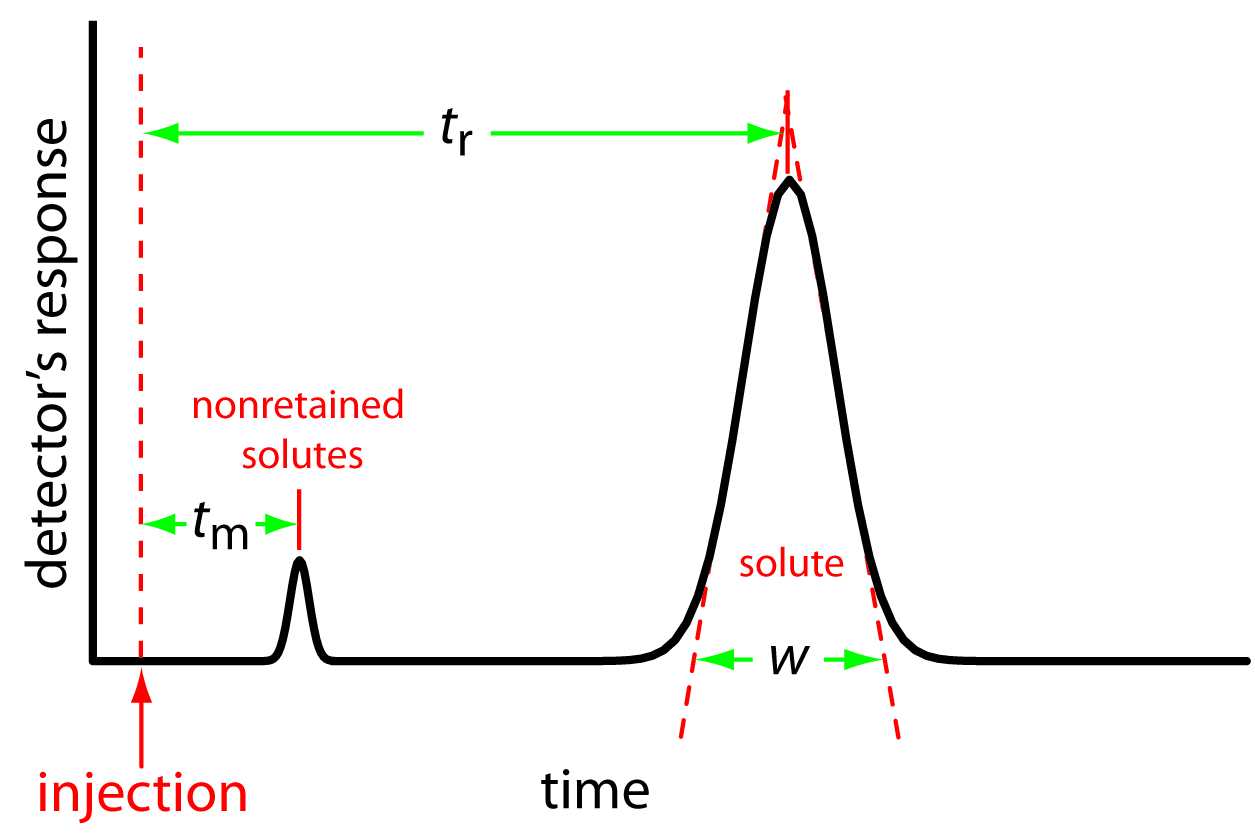
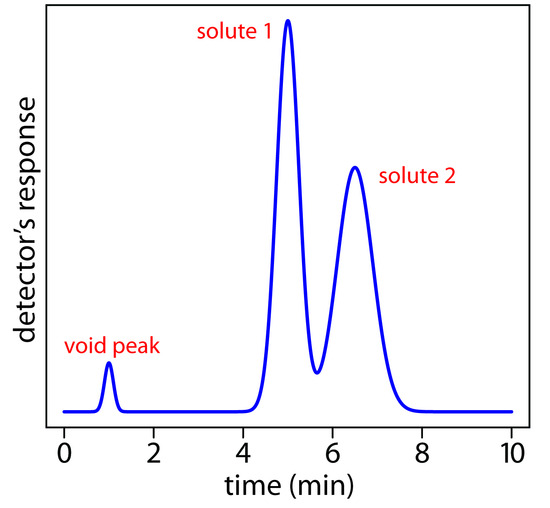
A solute’s chromatographic peak may be characterized in many ways, two of which are shown in Figure 12.9. Retention time, tr, is the time between the sample’s injection and the maximum response for the solute’s peak. Another important parameter is the baseline width, w, which, as shown in Figure 12.9, is determined by extending tangent lines from the inflection points on either side of the chromatographic peak through the baseline. Although usually we report tr and w using units of time, we can report them using units of volume by multiplying each by the mobile phase’s velocity, or in linear units by measuring distances with a ruler.
For example, a solute’s retention volume, Vr, is
\[V_r = t_r \times u\]
where u is the mobile phase’s velocity through the column.
In addition to the peak for the solute, Figure 12.9 also shows a small peak that elutes shortly after injecting the sample into the mobile phase. This peak is for nonretained solutes. Because these solutes do not interact with the stationary phase, they move through the column at the same rate as the mobile phase. The time required to elute nonretained solutes is called the column’s void time, tm.
Figure 12.9: Chromatogram showing a solute’s retention time, tr, and baseline width, w, and the column’s void time, tm, for nonretained solutes.
12.2.1 Chromatographic Resolution
The goal of chromatography is to separate a mixture into a series of chromatographic peaks, each representing a single component of the mixture. The resolution between two chromatographic peaks, RAB, is a quantitative measure of their separation, and is defined as
\[ R_\ce{AB}= \dfrac{t_\textrm{r,B} − t_\textrm{r,A} }{0.5(w_\ce{B} + w_\ce{A})} = \dfrac{2\Delta t_\ce{r}}{w_\ce{B} + w_\ce{A}} \tag{12.1}\]
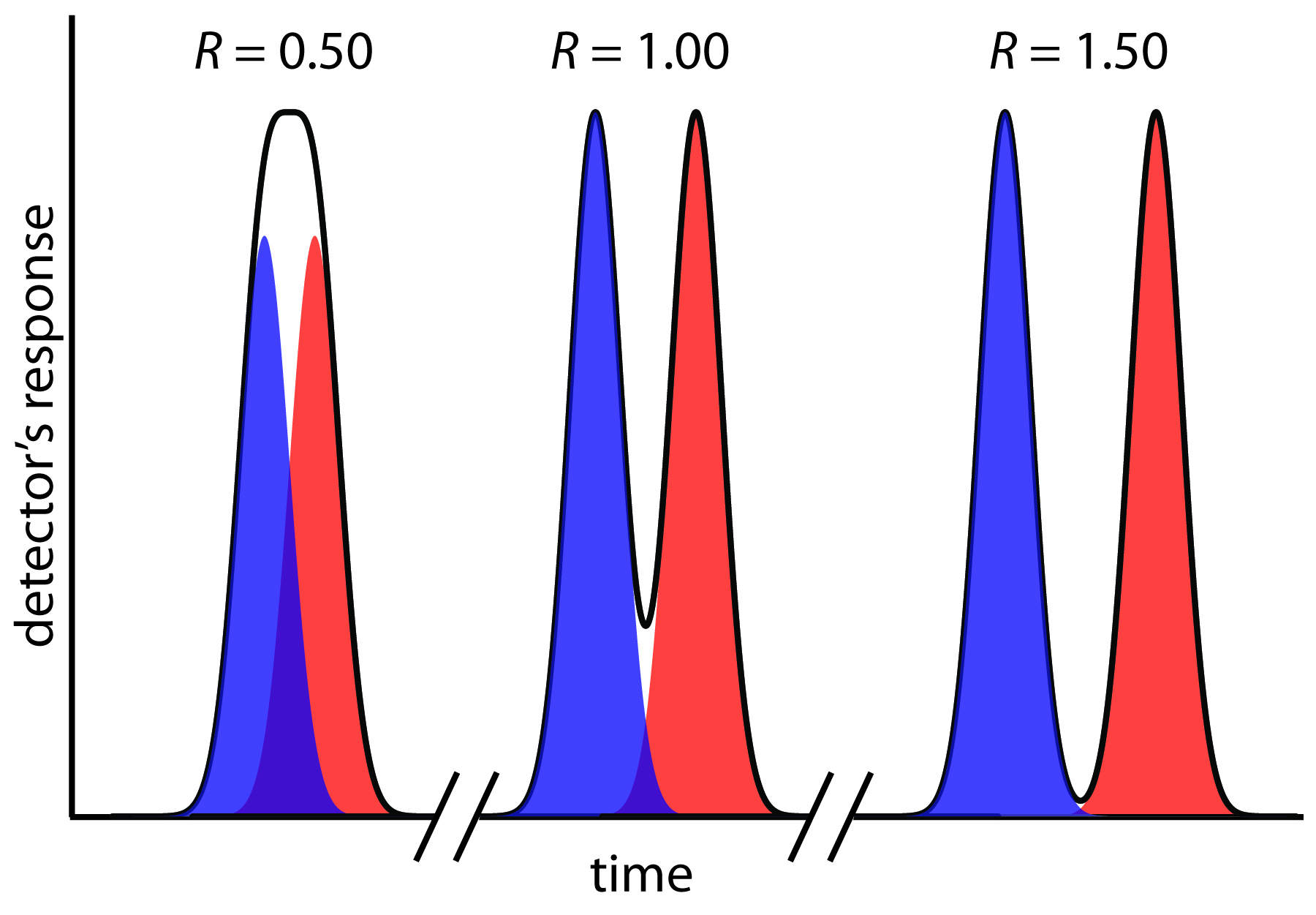
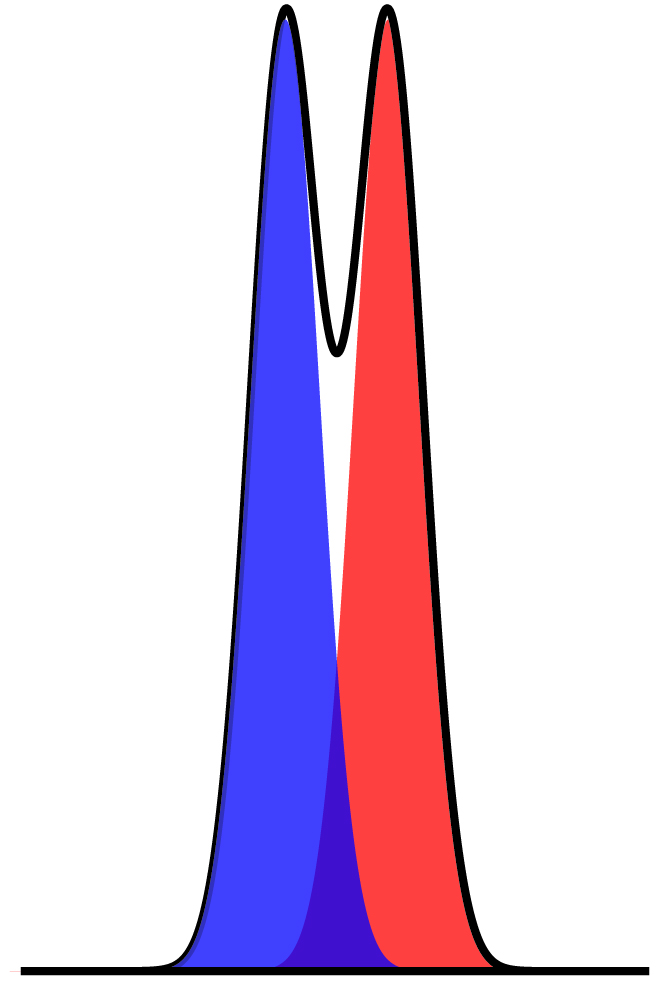
where B is the later eluting of the two solutes. As shown in Figure 12.10, the separation of two chromatographic peaks improves with an increase in RAB. If the areas under the two peaks are identical—as is the case in Figure 12.10—then a resolution of 1.50 corresponds to an overlap of only 0.13% for the two elution profiles. Because resolution is a quantitative measure of a separation’s success, it is a useful way to determine if a change in experimental conditions leads to a better separation.
Figure 12.10 Three examples showing the relationship between resolution and the separation of a two component mixture. The blue and red peaks are the elution profiles for the two components. The chromatographic peak—which is the sum of the two elution profiles—is shown by the solid black line.
Example 12.1
In a chromatographic analysis of lemon oil a peak for limonene has a retention time of 8.36 min with a baseline width of 0.96 min. γ-Terpinene elutes at 9.54 min with a baseline width of 0.64 min. What is the resolution between the two peaks?
Solution
Using equation 12.1 we find that the resolution is
\[R_\ce{AB} = \dfrac{2\Delta t_\ce{r}}{w_\ce{B} + w_\ce{A}} = \mathrm{\dfrac{2(9.54\: min − 8.36\: min)}{1.64\: min + 0.96\: min} = 1.48}\]
Exercise 12.1
Figure 12.11 shows the separation of a two-component mixture. What is the resolution between the two components? Use a ruler to measure ∆tr,wA, and wB in millimeters.
Figure 12.11 Chromatogram for Practice Exercise 12.1.
Click here to review your answer to this exercise.
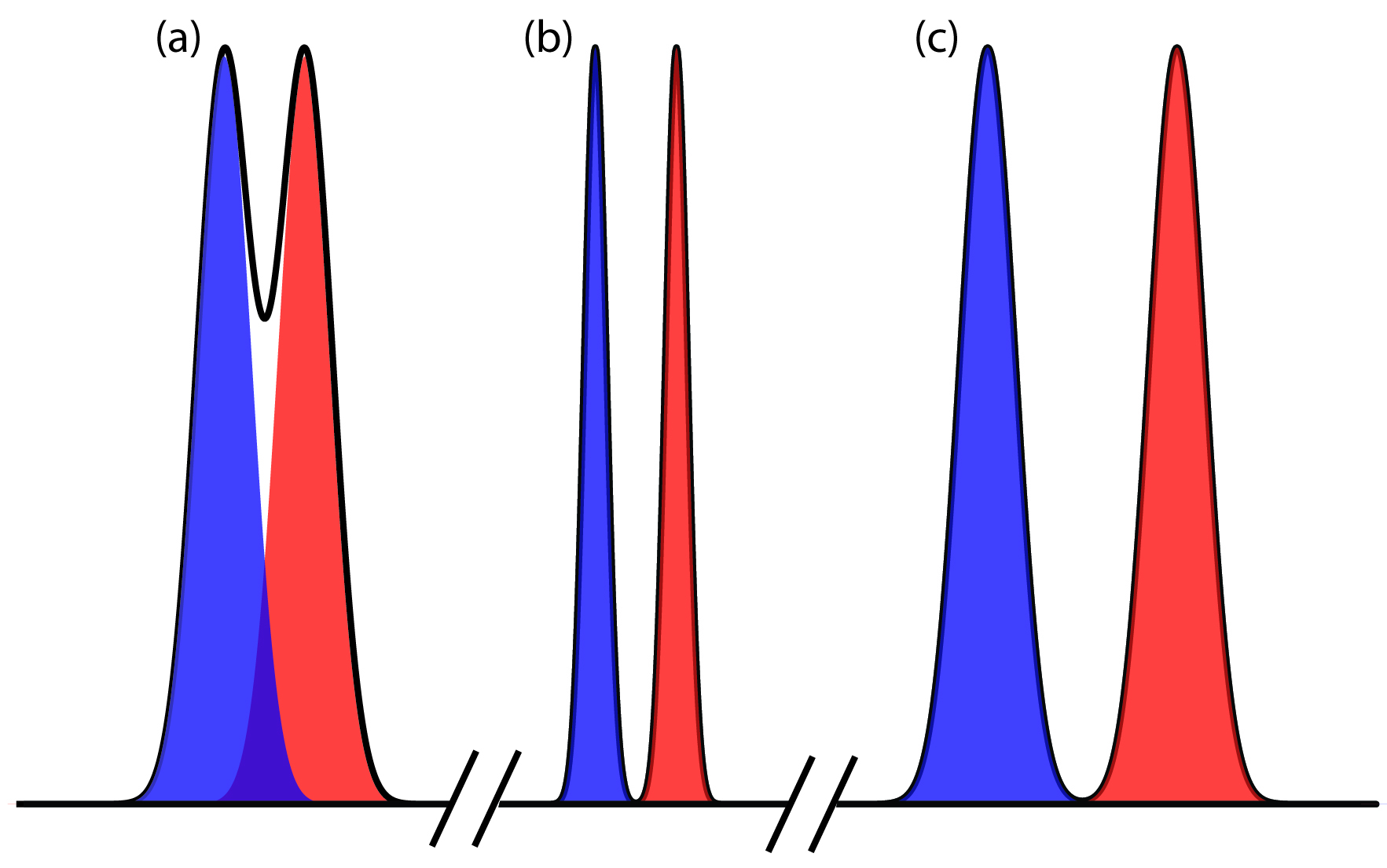
Equation 12.1 suggests that we can improve resolution by increasing ∆tr, or by decreasing wA and wB (Figure 12.12). To increase ∆tr we can use one of two strategies. One approach is to adjust the separation conditions so that both solutes spend less time in the mobile phase—that is, we increase each solute’s retention factor—which provides more time to effect a separation. A second approach is to increase selectivity by adjusting conditions so that only one solute experiences a significant change in its retention time. The baseline width of a solute’s peak depends on the solutes movement within and between the mobile phase and the stationary phase, and is governed by several factors that we collectively call column efficiency. We will consider each of these approaches for improving resolution in more detail, but first we must define some terms.
Figure 12.12: Two method for improving chromatographic resolution: (a) original chromatogram; (b) chromatogram after decreasing wA and wB by 4×; (c) chromatogram after increasing ∆tr by 2×.
12.2.2 Solute Retention Factor
Let’s assume that we can describe a solute’s distribution between the mobile phase and stationary phase using the following equilibrium reaction
\[\mathrm{S_m \rightleftharpoons S_s}\]
where
- \(\mathrm{S_m}\) is the solute in the mobile phase and
- \(\mathrm{S_s}\) is the solute in the stationary phase.
Note
This is not a trivial assumption. In this section we are, in effect, treating the solute’s equilibrium between the mobile phase and the stationary phase as if it is identical to the equilibrium in a liquid–liquid extraction. You might question whether this is a reasonable assumption.
There is an important difference between the two experiments we need to consider. In a liquid–liquid extraction, which takes place in a separatory funnel, the two phases remain in contact with each other at all times, allowing for a true equilibrium. In chromatography, however, the mobile phase is in constant motion. A solute moving into the stationary phase from the mobile phase equilibrates back into a different portion of the mobile phase; this does not describe a true equilibrium.
So, we ask again: Can we treat a solute’s distribution between the mobile phase and the stationary phase as an equilibrium process? The answer is yes, if the mobile phase velocity is slow relative to the kinetics of the solute’s moving back and forth between the two phase. In general, this is a reasonable assumption.
Following the same approach that we used in Section 7G.2 for liquid–liquid extractions, the equilibrium constant for this reaction is an equilibrium partition coefficient, KD.
\[K_\ce{D} = \mathrm{\dfrac{[S_s]}{[S_m]}}\]
In the absence of any additional equilibrium reactions in the mobile phase or stationary phase, KD is equivalent to the distribution ratio, D,
\[D = \mathrm{\dfrac{[S_s]}{[S_m]} = \dfrac{(mol\: S)_s / \mathit{V}_s}{(mol\: S)_m / \mathit{V}_m} = \mathit{K}_D}\tag{12.2}\]
where Vs and Vm are the volumes of the stationary phase and the mobile phase, respectively.
A conservation of mass requires that the total moles of solute remain constant throughout the separation; thus, we know that the following equation is true.
\[\mathrm{(mol\: S)_{total} = (mol\: S)_m + (mol\: S)_s}\tag{12.3}\]
Solving equation 12.3 for the moles of solute in the stationary phase and substituting into equation 12.2 leaves us with
\[D = \mathrm{\dfrac{\left\{(mol\: S)_{total} - (mol\: S)_s\right\}/\mathit{V}_s}{(mol\: S)_m / \mathit{V}_m}}\]
Rearranging this equation and solving for the fraction of solute in the mobile phase, fm, gives a result
\[f_m= \mathrm{\dfrac{(mol\: S)_m}{(mol\: S)_{total}}} =\dfrac{V_\ce{m}}{(DV_\ce{s} + V_\ce{m})}\tag{12.4}\]
that is identical to equation 7.26 for a liquid–liquid extraction. Because we may not know the exact volumes of the stationary phase and the mobile phase, we can simplify equation 12.4 by dividing both the numerator and the denominator by Vm; thus
\[f_m= \dfrac{V_\ce{m} / V_\ce{m}}{DV_\ce{s} / V_\ce{m} + V_\ce{m} / V_\ce{m}} = \dfrac{1}{DV_\ce{s} / V_\ce{m} + 1} = \dfrac{1}{1 + k}\tag{12.5}\]
where k
\[k = D × \dfrac{V_\ce{s}}{V_\ce{m}}\tag{12.6}\]
is the solute’s retention factor. Note that the larger the retention factor, the more the distribution ratio favors the stationary phase, leading to a more strongly retained solute and a longer retention time.
Note
The retention factor is also called the capacity factor, the capacity ratio, and the partition ratio, and is sometimes given the symbol k′. Keep this in mind if you are using other resources. Retention factor is the approved name from the IUPAC Gold Book.
We can determine a solute’s retention factor from a chromatogram by measuring the column’s void time, tm, and the solute’s retention time, tr (see Figure 12.9). Solving equation 12.5 for k, we find that
\[k = \dfrac{1 - f_\ce{m}}{f_\ce{m}}\tag{12.7}\]
Earlier we defined fm as the fraction of solute in the mobile phase. Assuming a constant mobile phase velocity, we also can define fm as
\[f_\ce{m} = \dfrac{\textrm{time spent in mobile phase}}{\textrm{total time spent on column}} = \dfrac{t_\ce{m}}{t_\ce{r}}\]
Substituting back into equation 12.7 and rearranging leaves us with
\[k = \dfrac{1 - \dfrac{t_\ce{m}}{t_\ce{r}}}{\dfrac{t_\ce{m}}{t_\ce{r}}} = \dfrac{t_\ce{r} − t_\ce{m}}{t_\ce{m}} =\dfrac{t^′_\ce{r}}{t_\ce{m}}\tag{12.8}\]
where t′r is the adjusted retention time.
Example 12.2
In a chromatographic analysis of low molecular weight acids, butyric acid elutes with a retention time of 7.63 min. The column’s void time is 0.31 min. Calculate the retention factor for butyric acid.
Solution
\[k_\ce{but}= \dfrac{t_\ce{r} - t_\ce{m}}{t_\ce{m}}= \mathrm{\dfrac{7.63\: min - 0.31\: min}{0.31\: min} = 23.6}\]
Practice Exercise 12.2
Figure 12.13 is the chromatogram for a two-component mixture. Determine the retention factor for each solute assuming the sample was injected at time t = 0.
Click here to review your answer to this exercise.
Figure 12.13 Chromatogram for Practice Exercise 12.2.
12.2.3 Selectivity
Selectivity is a relative measure of the retention of two solutes, which we define using a selectivity factor, α
\[α = \dfrac{k_\ce{B}}{k_\ce{A}} = \dfrac{t_\textrm{r,B} - t_\ce{m}}{t_\textrm{r,A} - t_\ce{m}}\tag{12.9}\]
where solute A always has the smaller retention time. When two solutes elute with identical retention time, α = 1.00; for all other conditions α > 1.00.
Example 12.3
In the chromatographic analysis for low molecular weight acids described in Example 12.2, the retention time for isobutyric acid is 5.98 min. What is the selectivity factor for isobutyric acid and butyric acid?
Solution
First we must calculate the retention factor for isobutyric acid. Using the void time from Example 12.2.
\[k_\ce{iso}= \dfrac{t_\ce{r} - t_\ce{m}}{t_\ce{m}} = \mathrm{\dfrac{5.98\: min − 0.31\: min}{0.31\: min} = 18.3}\]
The selectivity factor, therefore, is
\[α = \dfrac{k_\ce{but}}{k_\ce{iso}} =\dfrac{23.6}{18.3} = 1.29\]
Practice Exercise 12.3
Determine the selectivity factor for the chromatogram in Practice Exercise 12.2.
Click here to review your answer to this exercise.
12.2.4 Column Efficiency
Suppose we inject a sample consisting of a single component. At the moment of injection the sample occupies a narrow band of finite width. As the sample passes through the column, the width of this band continually increases in a process we call band broadening. Column efficiency provides a quantitative measure of the extent of band broadening.
Note
See Figure 12.6 and Figure 12.7. When we inject the sample it has a uniform, or rectangular concentration profile with respect to distance down the column. As it passes through the column, the band broadens and takes on a Gaussian concentration profile.
In their original theoretical model of chromatography, Martin and Synge divided the chromatographic column into discrete sections—what they called theoretical plates—in which there is an equilibrium partitioning of the solute between the stationary phase and the mobile phase.2 They described column efficiency in terms of the number of theoretical plates, N,
\[N = \dfrac{L}{H}\tag{12.10}\]
where L is the column’s length and H is the height of a theoretical plate. Column efficiency improves—and chromatographic peaks become narrower—when there are more theoretical plates.
If we assume that a chromatographic peak has a Gaussian profile, then the extent of band broadening is given by the peak’s variance or standard deviation. The height of a theoretical plate is the variance per unit length of the column
\[H = \dfrac{σ^2}{L}\tag{12.11}\]
where the standard deviation, σ, has units of distance. Because retention times and peak widths are usually measured in seconds or minutes, it is more convenient to express the standard deviation in units of time, τ, by dividing σ by the solute’s average linear velocity, ν.
\[τ = \dfrac{σ}{\overline{ν}} = \dfrac{σt_\ce{r}}{L}\tag{12.12}\]
Note
The solute’s average linear velocity is the distance it travels, L, divided by its retention time, tr.
For a Gaussian peak shape, the width at the baseline, w, is four times its standard deviation, τ.
\[w = 4τ\tag{12.13}\]
Combining equation 12.11, equation 12.12, and equation 12.13 defines the height of a theoretical plate in terms of the easily measured chromatographic parameters tr and w.
\[H = \dfrac{Lw^2}{16t_\ce{r}^2}\tag{12.14}\]
Note
See Figure 12.9 for a review of how to determine values for tr and w.
Combing equation 12.14 and equation 12.10 gives the number of theoretical plates.
\[N = 16\dfrac{t_r^2}{w^2}\tag{12.15}\]
Example 12.4
A chromatographic analysis for the chlorinated pesticide Dieldrin gives a peak with a retention time of 8.68 min and a baseline width of 0.29 min. What is the number of theoretical plates? Given that the column is 2.0 m long, what is the height of a theoretical plate in mm?
Solution
Using equation 12.15, the number of theoretical plates is
\[N = 16 \dfrac{t_r^2}{w^2} = N = \mathrm{16\dfrac{(8.68\: min)^2}{(0.29\: min)^2} = 14300\: plates}\]
Solving equation 12.10 for H gives the average height of a theoretical plate as
\[H = \dfrac{L}{N} = \mathrm{\dfrac{2.0\: m}{14300\: plates} × \dfrac{1000\: mm}{m} = 0.14\: mm/plate}\]
Practice Exercise 12.4
For each solute in the chromatogram for Practice Exercise 12.2, calculate the number of theoretical plates and the average height of a theoretical plate. The column is 0.5 m long.
Click here to review your answer to this exercise.
It is important to remember that a theoretical plate is an artificial construct and that a chromatographic column does not contain physical plates. In fact, the number of theoretical plates depends on both the properties of the column and the solute. As a result, the number of theoretical plates for a column may vary from solute to solute.
12.2.5 Peak Capacity
One advantage of improving column efficiency is that we can separate more solutes with baseline resolution. One estimate of the number of solutes that we can separate is
\[n_\ce{c} = 1 + \dfrac{\sqrt{N}}{4}\ln\dfrac{V_\ce{max}}{V_\ce{min}}\tag{12.16}\]
where nc is the column’s peak capacity, and Vmin and Vmax are the smallest and the largest volumes of mobile phase in which we can elute and detect a solute.3
Note
The smallest volume we can use is the column’s void volume. The largest volume is determined either by our patience—what is the maximum analysis time we can tolerate—or by our inability to detect solutes because there is too much band broadening.
A column with 10 000 theoretical plates, for example, can resolve no more than
\[n_\ce{c} = \mathrm{1 + \dfrac{\sqrt{10000}}{4}\ln\dfrac{30\: mL}{1\: mL} = 86\: solutes}\]
if Vmin and Vmax are 1 mL and 30 mL, respectively. This estimate provides an upper bound on the number of solutes and may help us exclude from consideration a column that does not have enough theoretical plates to separate a complex mixture. Just because a column’s theoretical peak capacity is larger than the number of solutes, however, does not mean that a separation is feasible. In most situations the practical peak capacity is less than the estimated value because the retention characteristics of some solutes are so similar that a separation is impossible. Nevertheless, columns with more theoretical plates, or with a greater range of possible elution volumes, are more likely to separate a complex mixture.
12.2.6 Asymmetric Peaks
Our treatment of chromatography in this section assumes that a solute elutes as a symmetrical Gaussian peak, such as that shown in Figure 12.9. This ideal behavior occurs when the solute’s partition coefficient, KD
\[K_\ce{D} = \mathrm{\dfrac{[S_s]}{[S_m]}}\]
is the same for all concentrations of solute. If this is not the case, then the chromatographic peak has an asymmetric peak shape similar to those shown in Figure 12.14. The chromatographic peak in Figure 12.14a is an example of peak tailing, which occurs when some sites on the stationary phase retain the solute more strongly than other sites. Figure 12.14b, which is an example of peak fronting is most often the result of overloading the column with sample.
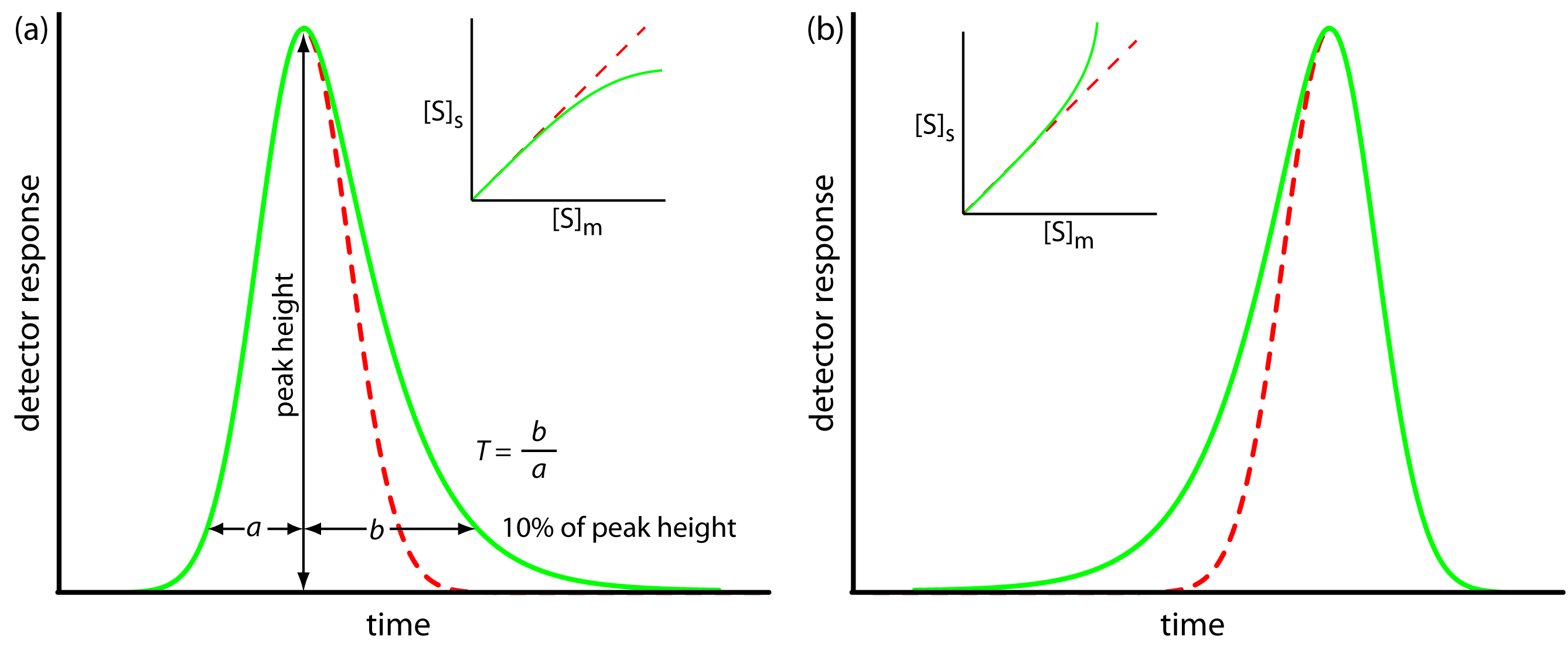
Figure 12.14 Examples of asymmetric chromatographic peaks showing (a) peak tailing and (b) peak fronting. For both (a) and (b) the green chromatogram is the asymmetric peak and the red dashed chromatogram shows the ideal, Gaussian peak shape. The insets show the relationship between the concentration of solute in the stationary phase, [S]s, and its concentration in the mobile phase, [S]m. The dashed red lines are for ideal behavior (KD is constant for all conditions) and the green lines show nonideal behavior (KD decreases or increases for higher total concentrations of solute). A quantitative measure of peak tailing, T, is shown in (a).
As shown in Figure 12.14a, we can report a peak’s asymmetry by drawing a horizontal line at 10% of the peak’s maximum height and measuring the distance from each side of the peak to a line drawn vertically through the peak’s maximum. The asymmetry factor, T, is defined as
\[T = \dfrac{b}{a}\]
The number of theoretical plates for an asymmetric peak shape is approximately
\[N ≈ \dfrac{41.7 × \dfrac{t_r^2}{(w_{0.1})^2}}{T + 1.25} = \dfrac{41.7 ×\dfrac{t_r^2}{(a + b)^2}}{T + 1.25}\]
where w0.1 is the width at 10% of the peak’s height.4
Note
Asymmetric peaks have fewer theoretical plates, and the more asymmetric the peak the smaller the number of theoretical plates. For example, the following table gives values for N for a solute eluting with a retention time of 10.0 min and a peak width of 1.00 min.
|
b |
a |
T |
N |
|
0.5 |
0.5 |
1.00 |
1850 |
|
0.6 |
0.4 |
1.50 |
1520 |
|
0.7 |
0.3 |
2.33 |
1160 |
|
0.8 |
0.2 |
4.00 |
790 |
|
0.9 |
0.1 |
9.00 |
410 |