6.2.3.1: Arrhenius Equation
- Page ID
- 1443
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)It is common knowledge that chemical reactions occur more rapidly at higher temperatures. Milk turns sour much more rapidly if stored at room temperature rather than in a refrigerator; butter goes rancid more quickly in the summer than in the winter; and eggs hard-boil more quickly at sea level than in the mountains. For the same reason, cold-blooded animals such as reptiles and insects tend to be more lethargic on cold days.
The reason for this is not hard to understand. Thermal energy relates direction to motion at the molecular level. As the temperature rises, molecules move faster and collide more vigorously, greatly increasing the likelihood of bond cleavages and rearrangements. Whether it is through the collision theory, transition state theory, or just common sense, chemical reactions are typically expected to proceed faster at higher temperatures and slower at lower temperatures.
By 1890 it was common knowledge that higher temperatures speed up reactions, often doubling the rate for a 10-degree rise, but the reasons for this were not clear. Finally, in 1899, the Swedish chemist Svante Arrhenius (1859-1927) combined the concepts of activation energy and the Boltzmann distribution law into one of the most important relationships in physical chemistry:
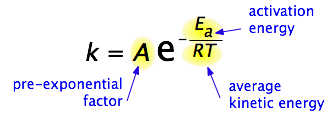
Take a moment to focus on the meaning of this equation, neglecting the A factor for the time being. First, note that this is another form of the exponential decay law discussed in the previous section of this series. What is "decaying" here is not the concentration of a reactant as a function of time, but the magnitude of the rate constant as a function of the exponent –Ea /RT. And what is the significance of this quantity? Recalling that RT is the average kinetic energy, it becomes apparent that the exponent is just the ratio of the activation energy Ea to the average kinetic energy. The larger this ratio, the smaller the rate (hence the negative sign). This means that high temperature and low activation energy favor larger rate constants, and thus speed up the reaction. Because these terms occur in an exponent, their effects on the rate are quite substantial.
The two plots below show the effects of the activation energy (denoted here by E‡) on the rate constant. Even a modest activation energy of 50 kJ/mol reduces the rate by a factor of 108.
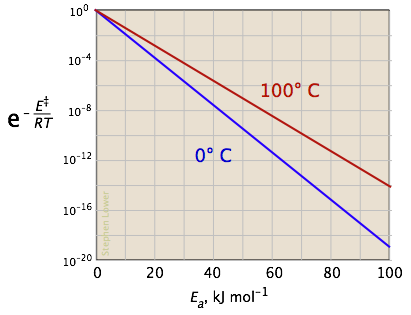
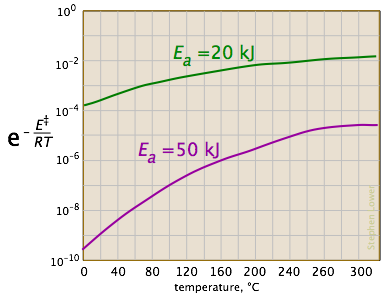
Looking at the role of temperature, a similar effect is observed. (If the x-axis were in "kilodegrees" the slopes would be more comparable in magnitude with those of the kilojoule plot at the above right.)
Determining the Activation Energy
The Arrhenius equation,
\[k = A e^{-E_a/RT} \label{1} \]
can be written in a non-exponential form that is often more convenient to use and to interpret graphically. Taking the logarithms of both sides and separating the exponential and pre-exponential terms yields
\[\begin{align} \ln k &= \ln \left(Ae^{-E_a/RT} \right) \\[4pt] &= \ln A + \ln \left(e^{-E_a/RT}\right) \label{2} \\[4pt] &= \left(\dfrac{-E_a}{R}\right) \left(\dfrac{1}{T}\right) + \ln A \label{3} \end{align} \]
Equation \ref{3} is in the form of \(y = mx + b\) - the equation of a straight line.
\[ \ln k=\ln A - \dfrac{E_{a}}{RT} \nonumber \]
where temperature is the independent variable and the rate constant is the dependent variable. So if one were given a data set of various values of \(k\), the rate constant of a certain chemical reaction at varying temperature \(T\), one could graph \(\ln (k)\) versus \(1/T\). From the graph, one can then determine the slope of the line and realize that this value is equal to \(-E_a/R\). One can then solve for the activation energy by multiplying through by -R, where R is the gas constant.
This affords a simple way of determining the activation energy from values of k observed at different temperatures, by plotting \(\ln k\) as a function of \(1/T\).
For the isomerization of cyclopropane to propene,

the following data were obtained (calculated values shaded in pink):
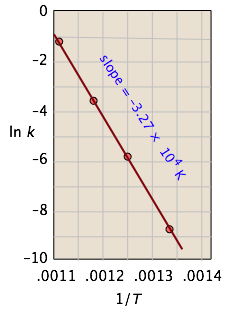
| T, °C | 477 | 523 | 577 | 623 |
|---|---|---|---|---|
| 1/T, K–1 × 103 | 1.33 | 1.25 | 1.18 | 1.11 |
| k, s–1 | 0.00018 | 0.0027 | 0.030 | 0.26 |
| ln k | –8.62 | –5.92 | –3.51 | –1.35 |
From the calculated slope, we have
\[\begin{align*} –\left(\dfrac{E_a}{R}\right) &= –3.27 \times 10^4 K \\ E_a &=– (8.314\, J\, mol^{–1} K^{–1}) (–3.27 \times 10^4\, K) \\[4pt] &= 273\, kJ\, mol^{–1} \end{align*} \]
Comment: This activation energy is high, which is not surprising because a carbon-carbon bond must be broken in order to open the cyclopropane ring. (C–C bond energies are typically around 350 kJ/mol.) This is why the reaction must be carried out at high temperature.
Calculating \(E_a\) without a plot
Because the ln k-vs.-1/T plot yields a straight line, it is often convenient to estimate the activation energy from experiments at only two temperatures. To see how this is done, consider that
\[\begin{align*} \ln k_2 -\ln k_1 &= \left(\ln A - \frac{E_a}{RT_2} \right) - \left(\ln A - \frac{E_a}{RT_1} \right) \\[4pt] &= \color{red}{\boxed{\color{black}{ \frac{E_a}{R}\left( \frac{1}{T_1}-\frac{1}{T_2} \right) }}} \end{align*} \]
The ln-A term is eliminated by subtracting the expressions for the two ln-k terms.) Solving the expression on the right for the activation energy yields
\[ E_a = \dfrac{R \ln \dfrac{k_2}{k_1}}{\dfrac{1}{T_1}-\dfrac{1}{T_2}} \nonumber \]
A widely used rule-of-thumb for the temperature dependence of a reaction rate is that a ten degree rise in the temperature approximately doubles the rate. This is not generally true, especially when a strong covalent bond must be broken. For a reaction that does show this behavior, what would the activation energy be?
Solution
Center the ten degree interval at 300 K. Substituting into the above expression yields
\[\begin{align*} E_a &= \dfrac{(8.314)(\ln 2/1)}{\dfrac{1}{295} – \dfrac{1}{305}} \\[4pt] &= \dfrac{(8.314\text{ J mol}^{-1}\text{ K}^{-1})(0.693)}{0.00339\,\text{K}^{-1} – 0.00328 \, \text{K}^{-1}} \\[4pt] &= \dfrac{5.76\, J\, mol^{–1} K^{–1}}{(0.00011\, K^{–1}} \\[4pt] &= 52,400\, J\, mol^{–1} = 52.4 \,kJ \,mol^{–1} \end{align*} \]
It takes about 3.0 minutes to cook a hard-boiled egg in Los Angeles, but at the higher altitude of Denver, where water boils at 92°C, the cooking time is 4.5 minutes. Use this information to estimate the activation energy for the coagulation of egg albumin protein.
Solution
The ratio of the rate constants at the elevations of Los Angeles and Denver is 4.5/3.0 = 1.5, and the respective temperatures are \(373 \; \rm{K }\) and \(365\; \rm{K}\). With the subscripts 2 and 1 referring to Los Angeles and Denver respectively:
\[\begin{align*} E_a &= \dfrac{(8.314)(\ln 1.5)}{\dfrac{1}{365\; \rm{K}} – \dfrac{1}{373 \; \rm{K}}} \\[4pt] &= \dfrac{(8.314)(0.405)}{0.00274 \; \rm{K^{-1}} – 0.00268 \; \rm{K^{-1}}} \\ &= \dfrac{(3.37\; \rm{J\; mol^{–1} K^{–1}})}{5.87 \times 10^{-5}\; \rm{K^{–1}}} \\[4pt] &= 57,400\; \rm{ J\; mol^{–1}} \\[4pt] &= 57.4 \; \rm{kJ \;mol^{–1}} \end{align*} \]
Comment: This low value seems reasonable because thermal denaturation of proteins primarily involves the disruption of relatively weak hydrogen bonds; no covalent bonds are broken (although disulfide bonds can interfere with this interpretation).
The Pre-exponential Factor
Up to this point, the pre-exponential term, \(A\) in the Arrhenius equation (Equation \ref{1}), has been ignored because it is not directly involved in relating temperature and activation energy, which is the main practical use of the equation.
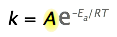
However, because \(A\) multiplies the exponential term, its value clearly contributes to the value of the rate constant and thus of the rate. Recall that the exponential part of the Arrhenius equation expresses the fraction of reactant molecules that possess enough kinetic energy to react, as governed by the Maxwell-Boltzmann law. This fraction can run from zero to nearly unity, depending on the magnitudes of \(E_a\) and of the temperature.
If this fraction were 0, the Arrhenius law would reduce to
\[k = A \nonumber \]
In other words, \(A\) is the fraction of molecules that would react if either the activation energy were zero, or if the kinetic energy of all molecules exceeded \(E_a\) — admittedly, an uncommon scenario (although barrierless reactions have been characterized).
What would limit the rate constant if there were no activation energy requirements? The most obvious factor would be the rate at which reactant molecules come into contact. This can be calculated from kinetic molecular theory and is known as the frequency- or collision factor, \(Z\).
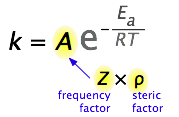
In some reactions, the relative orientation of the molecules at the point of collision is important, so a geometrical or steric factor (commonly denoted by \(\rho\)) can be defined. In general, we can express \(A\) as the product of these two factors:
\[A = Z\rho \nonumber \]
Values of \(ρ\) are generally very difficult to assess; they are sometime estimated by comparing the observed rate constant with the one in which \(A\) is assumed to be the same as \(Z\).
Implications
The exponential term in the Arrhenius equation implies that the rate constant of a reaction increases exponentially when the activation energy decreases. Because the rate of a reaction is directly proportional to the rate constant of a reaction, the rate increases exponentially as well. Because a reaction with a small activation energy does not require much energy to reach the transition state, it should proceed faster than a reaction with a larger activation energy.
In addition, the Arrhenius equation implies that the rate of an uncatalyzed reaction is more affected by temperature than the rate of a catalyzed reaction. This is because the activation energy of an uncatalyzed reaction is greater than the activation energy of the corresponding catalyzed reaction. Since the exponential term includes the activation energy as the numerator and the temperature as the denominator, a smaller activation energy will have less of an impact on the rate constant compared to a larger activation energy. Hence, the rate of an uncatalyzed reaction is more affected by temperature changes than a catalyzed reaction.
The Math in Eliminating the Constant A
To eliminate the constant \(A\), there must be two known temperatures and/or rate constants. With this knowledge, the following equations can be written:
\[ \ln k_{1}=\ln A - \dfrac{E_{a}}{RT_1} \label{a1} \]
at \(T_1\) and
\[ \ln k_{2}=\ln A - \dfrac{E_{a}}{RT_2} \label{a2} \]
at \(T_2\). By rewriting Equation \ref{a2}:
\[ \ln A = \ln k_{2} + \dfrac{E_{a}}{RT_2} \label{a3} \]
and substitute for \(\ln A\) into Equation \ref{a1}:
\[ \ln k_{1}= \ln k_{2} + \dfrac{E_{a}}{RT_2} - \dfrac{E_{a}}{RT_1} \label{a4} \]
This simplifies to:
\[\begin{align*} \ln k_{1} - \ln k_{2} &= -\dfrac{E_{a}}{RT_1} + \dfrac{E_{a}}{RT_2} \\[4pt] \ln \dfrac{k_{1}}{k_{2}} &= -\dfrac{E_{a}}{R} \left (\dfrac{1}{T_1}-\dfrac{1}{T_2} \right ) \end{align*} \]
Summary
After observing that many chemical reaction rates depended on the temperature, Arrhenius developed this equation to characterize the temperature-dependent reactions:
\[ k=Ae^{^{\frac{-E_{a}}{RT}}} \nonumber \]
or
\[\ln k=\ln A - \frac{E_{a}}{RT} \nonumber \]
with the following terms:
\(k\): Chemical reaction rate constant
- In unit of s-1(for 1st order rate constant) or M-1s-1(for 2nd order rate constant)
\(A\): The pre-exponential factor or frequency factor
- Specifically relates to molecular collision
- Deals with the frequency of molecules that collide in the correct orientation and with enough energy to initiate a reaction.
- It is a factor that is determined experimentally, as it varies with different reactions.
- In unit of L mol-1s-1 or M-1s-1(for 2nd order rate constant) and s-1(for 1st order rate constant)
- Because frequency factor A is related to molecular collision, it is temperature dependent
- Hard to extrapolate pre-exponential factor because lnk is only linear over a narrow range of temperature
\(E_a\): The activation energy is the threshold energy that the reactant(s) must acquire before reaching the transition state.
- Once in the transition state, the reaction can go in the forward direction towards product(s), or in the opposite direction towards reactant(s).
- A reaction with a large activation energy requires much more energy to reach the transition state.
- Likewise, a reaction with a small activation energy doesn't require as much energy to reach the transition state.
- In units of J/mol.
- -Ea/RT resembles the Boltzmann distribution law.
\(R\): The gas constant.
- Its value is 8.314 J/mol K.
\(T\): The absolute temperature at which the reaction takes place.
- In units of Kelvin (K).
Problems
- Find the activation energy (in kJ/mol) of the reaction if the rate constant at 600K is 3.4 M-1s-1 and 31.0 at 750K.
- Find the rate constant if the temperature is 289K, Activation Energy is 200kJ/mol and pre-exponential factor is 9 M-1s-1
- Find the new rate constant at 310K if the rate constant is 7 M-1s-1 at 370K, Activation Energy is 900kJ/mol
- Calculate the activation energy if the pre-exponential factor is 15 M-1s-1, rate constant is 12M-1s-1and it is at 22K
- Find the new temperature if the rate constant at that temperature is 15M-1s-1 while at temperature 389K the rate constant is 7M-1s1, the Activation Energy is 600kJ/mol
Solutions
1. Ea is the factor the question asks to be solved. Therefore it is much simpler to use
\(\large \ln k = -\frac{E_a}{RT} + \ln A\)
To find Ea, subtract ln A from both sides and multiply by -RT.
This will give us:
\( E_a=\ln A -\ln k)RT\)
2. Substitute the numbers into the equation:
\(\ ln k = \frac{-(200 \times 1000\text{ J}) }{ (8.314\text{ J mol}^{-1}\text{K}^{-1})(289\text{ K})} + \ln 9\)
k = 6.37X10-36 M-1s-1
3. Use the equation ln(k1/k2)=-Ea/R(1/T1-1/T2)
ln(7/k2)=-[(900 X 1000)/8.314](1/370-1/310)
k2=1.788X10-24 M-1s-1
4. Use the equation k = Ae-Ea/RT
12 = 15e-Ea/(8.314)(22)
Ea = 40.82J/mol
5. Use the equatioin ln(k1/k2)=-Ea/R(1/T1-1/T2)
ln(15/7)=-[(600 X 1000)/8.314](1/T1 - 1/389)
T1 = 390.6K
References
- Chang, Raymond. 2005. Physical Chemistry for the Biosciences. Sausalito (CA): University Science Books. p. 311-347.
- Segal, Irwin. 1975. Enzyme Kinetics. John Wiley & Sons, Inc. p.931-933.
- Ames, James. 2010. Lecture 7 Chem 107B. University of California, Davis.
- Laidler, Keith. "The Development of the Arrhenius Equation." J. Chem. Educ., 1984, 61 (6), p 494
- Logan, S. R. "The orgin and status of the Arrhenius Equation." J. Chem. Educ., 1982, 59 (4), p 279
Contributors and Attributions
- Guenevieve Del Mundo, Kareem Moussa, Pamela Chacha, Florence-Damilola Odufalu, Galaxy Mudda, Kan, Chin Fung Kelvin



