11.E: Electrochemistry (Exercises)
- Page ID
- 518137
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Redox reactions
What do oxidation and reduction mean in terms of electron transfer?
How does each process change the oxidation number of an element?
Can oxidation or reduction happen alone?
- Answer
-
Oxidation is the loss of electrons, which increases the oxidation number of an element.
Reduction is the gain of electrons, which decreases the oxidation number of an element.Oxidation and reduction always occur together in a chemical reaction because when one substance loses electrons (oxidation), another substance must gain those electrons (reduction). This is why these reactions are called redox (reduction-oxidation) reactions.
Consider the following redox reaction in acidic solution:
\[ \ce{MnO4^- (aq) + 5Fe^2+ (aq) + 8H+ (aq) \rightarrow Mn^2+ (aq) + 5Fe^3+ (aq) + 4H2O(l)} \nonumber \]
a) Identify which species is oxidized and which is reduced.
b) Identify the oxidizing agent and the reducing agent.
c) Write the oxidation half-reaction and the reduction half-reaction for this process.
- Answer
-
a) \(\ce{Fe^2+}\) (oxidation number of Fe: +2) → \(\ce{Fe^3+}\) (oxidation number of Fe: +3). The oxidation number increases, indicating a loss of electrons, which is oxidation.
\(\ce{MnO4^-}\) (oxidation number of Mn: +7) → \(\ce{Mn^2+}\) (oxidation number of Mn: +2). The oxidation number decreases, indicating a gain of electrons, which is reduction.
b) Oxidizing agent: \(\ce{MnO4^-}\), because it causes \(\ce{Fe^2+}\) to lose electrons while it is reduced itself.
Reducing agent: \(\ce{Fe^2+}\), because it donates the electrons to reduce \(\ce{MnO4^-}\).
c) Write the oxidation and reduction half-reactions:
Oxidation: \(\ce{Fe^2+ (aq) \rightarrow Fe^3+ (aq) + e^- }\)
Reduction: \(\ce{MnO4^- (aq) + 8H+ (aq) + 5e^- \rightarrow Mn^2+ (aq) + 4H2O(l)}\)
Consider the following redox reaction in basic solution:
\[ \ce{Zn(s) + 4OH- (aq) + Br2 (l) \rightarrow Zn(OH)4^2- (aq) + 2Br- (aq) } \nonumber \]
a) Identify which species is oxidized and which is reduced.
b) Identify the oxidizing agent and the reducing agent.
c) Write the oxidation half-reaction and the reduction half-reaction for this process.
- Answer
-
a) \(\ce{Zn}\) (oxidation number of Zn: 0) → \(\ce{Zn(OH)4^2-}\) (oxidation number of Zn: +2). The oxidation number increases, indicating a loss of electrons, which is oxidation.
\(\ce{Br2}\) (oxidation number of Br: 0) → \(\ce{Br-}\) (oxidation number of Br: -1). The oxidation number decreases, indicating a gain of electrons, which is reduction.
b) Oxidizing agent: \(\ce{Br2}\), because it causes \(\ce{Zn}\) to lose electrons while it is reduced itself.
Reducing agent: \(\ce{Zn}\), because it donates the electrons to reduce \(\ce{Br2}\).
c) Oxidation: \(\ce{Zn (s) + 4OH- (aq) \rightarrow Zn(OH)4^{2-} (aq) + 2e^- }\)
Reduction: \(\ce{Br2 (l) + 2e^- \rightarrow 2Br- (aq)}\)
Balance the following redox reactions in acidic solution.
a) \(\ce{Cu(s) + NO3^- (aq) \rightarrow Cu^2+ (aq) + NO(g)}\)
b) \(\ce{Cr2O7^2- (aq) + Ni(s) \rightarrow Cr^3+ (aq) + Ni^2+ (aq)}\)
c) \(\ce{MnO4^- (aq) + C2O4^2- (aq) \rightarrow CO2(g) + Mn^2+ (aq)}\)
- Answer
-
a) Step 1: Write skeletal equations for the oxidation and reduction half-reactions.
\[\begin{align*}
&\text { oxidation: } \quad \ce{Cu (s) -> Cu^{2+}(aq)} \\[4pt]
&\text { reduction: } \quad \ce{NO3^- (aq) -> NO(g)}
\end{align*} \nonumber \]Step 2: Balance each half-reaction for all elements except \(\ce{H}\) and \(\ce{O}\). Complete!
Step 3: Balance each half-reaction for \(\ce{\mathbf{O}}\) by adding \(\ce{\mathbf{H2O}}\):
\[\begin{align*}
&\text { oxidation: } \quad \ce{Cu (s) -> Cu^{2+}(aq)} \\[4pt]
&\text { reduction: } \quad \ce{NO3^- (aq) -> NO(g) + \mathbf{2 H2O(l)}}
\end{align*} \nonumber \]Step 4: Balance each half-reaction for \(\ce{\mathbf{H}}\) by adding \(\ce{\mathbf{H^{+}}}\):
\[\begin{align*}
&\text { oxidation: } \quad \ce{Cu (s) -> Cu^{2+}(aq)} \\[4pt]
&\text { reduction: } \quad \ce{\mathbf{4 H^{+}(aq)} + NO3^- (aq) -> NO(g) + 2 H2O(l)}
\end{align*} \nonumber \]Step 5: Balance each half-reaction for charge by adding electrons:
\[\begin{align*}
&\text { oxidation: } \quad \ce{Cu (s) -> Cu^{2+}(aq) + \mathbf{ 2 e^{-}}} \\[4pt]
&\text { reduction: } \quad \ce{\mathbf{3 e^{-}} + 4 H^{+}(aq) + NO3^- (aq) -> NO(g) + 2 H2O(l)}
\end{align*} \nonumber \]Step 6: If necessary, multiply one or both half-reactions so that the number of electrons gained equals the number lost:
\[\begin{align*}
&\text { oxidation: }(\times 3) \quad \ce{\mathbf{3}Cu (s) -> \mathbf{3}Cu^{2+}(aq) + \mathbf{6} e^{-}} \\[4pt]
&\text { reduction: }(\times 2) \quad \ce{\mathbf{6} e^{-} + \mathbf{8} H^{+}(aq) + \mathbf{2}NO3^- (aq) ->\mathbf{2} NO(g) + \mathbf{4} H2O(l)}
\end{align*} \nonumber \]Step 7: Add the two half-reactions and simplify:
\[\begin{align*}
\ce{3 Cu(s) + \cancel{6 e^{-}} + 8 H^{+}(aq) +2 NO3^- (aq) &-> 3 Cu^{2+}(aq) + \cancel{6 e^{-}} + 2 NO(g) + 4 H2O (l)} \\[4pt]
\ce{3 Cu(s) + 8 H^{+}(aq) + 2 NO3^- (aq) &-> 3 Cu^{2+}(aq) + 2 NO(g) + 4 H2O (l)}
\end{align*} \nonumber \]Final Check
Element Reactants Products Cu 3 3 H 8 8 N 2 2 O 6 6 Reactants: \( 3 \times 0 \, (\text{Cu}) + 8 \times (+1) \, (\ce{H^+}) + 2 \times (-1) \, (\ce{NO3^-}) = +6 \) Products: \( 3 \times (+2) \, (\ce{Cu^{2+}}) + 2 \times 0 \, (\ce{NO}) + 4 \times 0 \, (\ce{H2O}) = +6 \)
Both atoms and total charge are balanced.
b) Step 1: Write skeletal equations for the oxidation and reduction half-reactions:
\[\begin{align*}
&\text { oxidation: } \quad \ce{Ni (s) -> Ni^{2+}(aq)} \\[4pt]
&\text { reduction: } \quad \ce{Cr2O7^2- (aq) -> Cr^3+ (aq)} \end{align*} \]Step 2: Balance each half-reaction for all elements except \(\ce{H}\) and \(\ce{O}\).
\[\begin{align*}
&\text { oxidation: } \quad \ce{Ni (s) -> Ni^{2+}(aq)} \\[4pt]
&\text { reduction: } \quad \ce{Cr2O7^2- (aq) -> \mathbf{2}Cr^3+ (aq)} \end{align*} \]Step 3: Balance each half-reaction for \(\ce{\mathbf{O}}\) by adding \(\ce{\mathbf{H2O}}\):
\[\begin{align*}
&\text { oxidation: } \quad \ce{Ni (s) -> Ni^{2+}(aq)} \\[4pt]
&\text { reduction: } \quad \ce{Cr2O7^2- (aq) -> 2Cr^3+ (aq) + \mathbf{7H2O(l)} } \end{align*} \]Step 4: Balance each half-reaction for \(\ce{\mathbf{H}}\) by adding \(\ce{\mathbf{H^{+}}}\):
\[\begin{align*}
&\text { oxidation: } \quad \ce{Ni (s) -> Ni^{2+}(aq)} \\[4pt]
&\text { reduction: } \quad \ce{\mathbf{14 H^{+}(aq)} + Cr2O7^2- (aq) -> 2Cr^3+ (aq) + 7H2O(l)} \end{align*} \]Step 5: Balance each half-reaction for charge by adding electrons:
\[\begin{align*}
&\text { oxidation: } \quad \ce{Ni (s) -> Ni^{2+}(aq) + \mathbf{ 2 e^{-}}} \\[4pt]
&\text { reduction: } \quad \ce{\mathbf{ 6 e^{-}} + 14 H^{+}(aq) + Cr2O7^2- (aq) -> 2Cr^3+ (aq) + 7H2O(l)} \end{align*} \]Step 6: If necessary, multiply one or both half-reactions so that the number of electrons gained equals the number lost:
\[\begin{align*}
&\text { oxidation: }(\times 3) \quad \ce{\mathbf{3}Ni (s) -> \mathbf{3}Ni^{2+}(aq) + \mathbf{6} e^{-}} \\[4pt]
&\text { reduction: } \quad \ce{ 6 e^{-} + 14 H^{+}(aq) + Cr2O7^2- (aq) -> 2Cr^3+ (aq) + 7H2O(l)} \end{align*} \]Step 7: Add the two half-reactions and simplify:
\[\begin{align*}
\ce{3Ni (s) + \cancel{ 6 e^{-}} + 14 H^{+}(aq) + Cr2O7^2- (aq) &-> 3Ni^{2+}(aq) + \cancel{6 e^{-}} +2Cr^3+ (aq) + 7H2O(l)} \\[4pt]
\ce{3Ni (s) + 14 H^{+}(aq) + Cr2O7^2- (aq) &-> 3Ni^{2+}(aq) +2Cr^3+ (aq) + 7H2O(l)} \end{align*} \]Final Check
ChargeElement Reactants Products Ni 3 3 H 14 14 Cr 2 2 O 7 7 Reactants: +12, Products +12
Both atoms and total charge are balanced.
c) Step 1: Write skeletal equations for the oxidation and reduction half-reactions:
\[\begin{align*}
&\text { oxidation: } \quad \ce{C2O4^2- (aq) -> CO2(g)} \\[4pt]
&\text { reduction: } \quad \ce{MnO4^- (aq) -> Mn^2+ (aq)} \end{align*} \]Step 2: Balance each half-reaction for all elements except \(\ce{H}\) and \(\ce{O}\).
\[\begin{align*}
&\text { oxidation: } \quad \ce{C2O4^2- (aq) -> \mathbf{2}CO2(g)} \\[4pt]
&\text { reduction: } \quad \ce{MnO4^- (aq) -> Mn^2+ (aq)} \end{align*} \]Step 3: Balance each half-reaction for \(\ce{\mathbf{O}}\) by adding \(\ce{\mathbf{H2O}}\):
\[\begin{align*}
&\text { oxidation: } \quad \ce{C2O4^2- (aq) -> 2CO2(g)} \\[4pt]
&\text { reduction: } \quad \ce{MnO4^- (aq) -> Mn^2+ (aq) + \mathbf{4H2O(l)}} \end{align*} \]Step 4: Balance each half-reaction for \(\ce{\mathbf{H}}\) by adding \(\ce{\mathbf{H^{+}}}\):
\[\begin{align*}
&\text { oxidation: } \quad \ce{C2O4^2- (aq) -> 2CO2(g)} \\[4pt]
&\text { reduction: } \quad \ce{\mathbf{8 H^{+}(aq)} + MnO4^- (aq) -> Mn^2+ (aq) + 4H2O(l)} \end{align*} \]Step 5: Balance each half-reaction for charge by adding electrons:
\[\begin{align*}
&\text { oxidation: } \quad \ce{C2O4^2- (aq) -> 2CO2(g) +\mathbf{ 2e^{-}}} \\[4pt]
&\text { reduction: } \quad \ce{\mathbf{ 5e^{-}} + 8 H^{+}(aq) + MnO4^- (aq) -> Mn^2+ (aq) + 4H2O(l)} \end{align*} \]Step 6: If necessary, multiply one or both half-reactions so that the number of electrons gained equals the number lost:
\[\begin{align*}
&\text { oxidation: }(\times 5) \quad \ce{\mathbf{5}C2O4^2- (aq) -> \mathbf{10}CO2(g) + \mathbf{10}e^{-}} \\[4pt]
&\text { reduction: }(\times 2) \quad \ce{\mathbf{10}e^{-} + \mathbf{16}H^{+}(aq) + \mathbf{2}MnO4^- (aq) -> \mathbf{2}Mn^2+ (aq) + \mathbf{8}H2O(l)} \end{align*} \]Step 7: Add the two half-reactions and simplify:
\[\begin{align*}
\ce{5C2O4^2- (aq) + \cancel{10e^{-}} + 16H^{+}(aq) + 2MnO4^- (aq) &->10CO2(g) + \cancel{10e^{-}} + 2Mn^2+ (aq) + 8H2O(l)} \\[4pt]
\ce{5C2O4^2- (aq) + 16H^{+}(aq) + 2MnO4^- (aq) &->10CO2(g) + 2Mn^2+ (aq) + 8H2O(l)} \end{align*} \]Final Check
Charge: Reactants +4, Products +4Element Reactants Products C 10 10 O 28 28 H 16 16 Mn 2 2 Both atoms and total charge are balanced.
Balance the following redox reactions in basic solution.
a) \(\ce{MnO4^- (aq) + IO3^- (aq) -> IO4^- + MnO2 (s)}\)
b) \(\ce{Cr(OH)4^- (aq) + ClO- (aq) -> CrO4^2- (aq) + Cl2 (g)}\)
- Answer
-
a) Step 1: Write skeletal equations for the oxidation and reduction half-reactions.
\[\begin{align*}
&\text { oxidation: } \quad \ce{IO3^- (aq) -> IO4^- (aq)} \\[4pt]
&\text { reduction: } \quad \ce{MnO4^{-}(aq) -> MnO2(s)}
\end{align*} \]Step 2: Balance each half-reaction for all elements except \(\ce{H}\) and \(\ce{O}\). Complete!
Step 3: Balance each half-reaction for \(\ce{\mathbf{O}}\) by adding \(\ce{\mathbf{H2O}}\).
\[\begin{align*}
&\text { oxidation: } \quad \ce{\mathbf{H2O(l)} + IO3^- (aq) -> IO4^- (aq)} \\[4pt]
&\text { reduction: } \quad \ce{MnO4^{-}(aq) -> MnO2(s) + \mathbf{2H2O(l)}}
\end{align*} \]Step 4: Balance each half-reaction for \(\ce{\mathbf{H}}\) by adding \(\ce{\mathbf{H^{+}}}\).
\[\begin{align*}
&\text { oxidation: } \quad \ce{H2O(l) + IO3^- (aq) -> IO4^- (aq) + \mathbf{2H+ (aq)}} \\[4pt]
&\text { reduction: } \quad \ce{ \mathbf{4H+ (aq)} + MnO4^{-}(aq) -> MnO2(s) + 2H2O(l)}
\end{align*} \]Step 5: Balance each half-reaction for charge by adding electrons.
\[\begin{align*}
&\text { oxidation: } \quad \ce{H2O(l) + IO3^- (aq) -> IO4^- (aq) + 2H+ (aq) + \mathbf{2e- }} \\[4pt]
&\text { reduction: } \quad \ce{\mathbf{3e- } + 4H+ (aq) + MnO4^{-}(aq) -> MnO2(s) + 2H2O(l)}
\end{align*} \]Step 6: If necessary, multiply one or both half-reactions; so that the number of electrons gained equals the number lost.
\[\begin{align*}
&\text { oxidation: }(\times 3) \quad \ce{\mathbf{3}H2O(l) + \mathbf{3}IO3^- (aq) -> \mathbf{3}IO4^- (aq) + \mathbf{6}H+ (aq) + \mathbf{6}e- } \\[4pt]
&\text { reduction: }(\times 2) \quad \ce{\mathbf{6}e- + \mathbf{8}H+ (aq) + \mathbf{2}MnO4^{-}(aq) -> \mathbf{2}MnO2(s) + \mathbf{4}H2O(l)}
\end{align*} \]Step 7: Add the two half-reactions and simplify.
\[\begin{align*}
\ce{\cancel{3H2O(l)} + 3IO3^- (aq) + \cancel{6e- } + 2\cancel{8}H+ (aq) + 2MnO4^{-}(aq) &-> 3IO4^- (aq) + \cancel{6H+} (aq) + \cancel{6e- } + 2MnO2(s) + 1\cancel{4}H2O(l)} \\[4pt]
\ce{3IO3^- (aq) + 2H+ (aq) + 2MnO4^{-}(aq) &-> 3IO4^- (aq) + 2MnO2(s) + H2O(l)}
\end{align*} \]Step 8: If the reaction takes place in basic solution, add OH− ions to both sides to neutralize the H+ ions, then simplify (remembering that \(\ce{H+ + OH- \rightarrow H2O(l)}\)):
\[\begin{align*}
\ce{3IO3^- (aq) + \mathbf{2H+ (aq)} + \mathbf{2OH- (aq)} + 2MnO4^{-}(aq) &-> 3IO4^- (aq) + 2MnO2(s) + H2O(l)} + \mathbf{2OH^- (aq)}\\[4pt]
\ce{3IO3^- (aq) + \mathbf{2H2O(l)} + 2MnO4^{-}(aq) &-> 3IO4^- (aq) + 2MnO2(s) + H2O(l) + \mathbf{2OH^- (aq)}}\\[4pt]
\ce{3IO3^- (aq) + \cancel{2}H2O(l) + 2MnO4^{-}(aq) &-> 3IO4^- (aq) + 2MnO2(s) + \cancel{H2O(l)} + 2OH^- (aq)}
\end{align*} \]\[\ce{3IO3^- (aq) + H2O(l) + 2MnO4^{-}(aq) -> 3IO4^- (aq) + 2MnO2(s) + 2OH^- (aq)} \nonumber\]
Final Check
Element Reactants Products I 3 3 O 18 18 H 2 2 Mn 2 2 Total Charge:
Reactants: -3 + 0 + -2 = -5 Products: -3 + 0 + -2 = -5
Both atoms and total charge are balanced.
b) Step 1: Write skeletal equations for the oxidation and reduction half-reactions.
\[\begin{align*}
&\text { oxidation: } \quad \ce{Cr(OH)4^- (aq) -> CrO4^2- (aq)} \\[4pt]
&\text { reduction: } \quad \ce{ClO^{-}(aq) -> Cl2(g)}
\end{align*} \]Step 2: Balance each half-reaction for all elements except \(\ce{H}\) and \(\ce{O}\).
\[\begin{align*}
&\text { oxidation: } \quad \ce{Cr(OH)4^- (aq) -> CrO4^2- (aq)} \\[4pt]
&\text { reduction: } \quad \ce{\mathbf{2}ClO^{-}(aq) -> Cl2(g)}
\end{align*} \]Step 3: Balance each half-reaction for \(\ce{\mathbf{O}}\) by adding \(\ce{\mathbf{H2O}}\).
\[\begin{align*}
&\text { oxidation: } \quad \ce{Cr(OH)4^- (aq) -> CrO4^2- (aq)} \\[4pt]
&\text { reduction: } \quad \ce{2ClO^{-}(aq) -> Cl2(g) +\mathbf{2H2O(l)}}
\end{align*} \]Step 4: Balance each half-reaction for \(\ce{\mathbf{H}}\) by adding \(\ce{\mathbf{H^{+}}}\).\[\begin{align*}
&\text { oxidation: } \quad \ce{Cr(OH)4^- (aq) -> CrO4^2- (aq) + \mathbf{4H^{+}}} \\[4pt]
&\text { reduction: } \quad \ce{\mathbf{4H^{+}} + 2ClO^{-}(aq) -> Cl2(g) +2H2O(l)}
\end{align*} \]Step 5: Balance each half-reaction for charge by adding electrons.
\[\begin{align*}
&\text { oxidation: } \quad \ce{Cr(OH)4^- (aq) -> CrO4^2- (aq) + 4H^{+} + \mathbf{3e- }} \\[4pt]
&\text { reduction: } \quad \ce{\mathbf{2e- } + 4H^{+} + 2ClO^{-}(aq) -> Cl2(g) + 2H2O(l)}
\end{align*} \]Step 6: If necessary, multiply one or both half-reactions; so that the number of electrons gained equals the number lost.
\[\begin{align*}
&\text { oxidation:(x2): } \quad \ce{\mathbf{2}Cr(OH)4^- (aq) -> \mathbf{2}CrO4^2- (aq) + \mathbf{8}H^{+} + \mathbf{6}e- } \\[4pt]
&\text { reduction(x3): } \quad \ce{\mathbf{6}e- + \mathbf{12}H^{+} + \mathbf{6}ClO^{-}(aq) -> \mathbf{3}Cl2(g) +\mathbf{6}H2O(l)}
\end{align*} \]Step 7: Add the two half-reactions and simplify.
\[\begin{align*}
\ce{2Cr(OH)4^- (aq) + \cancel{6e-} + \mathbf{4}\cancel{12}H^{+} + 6ClO^{-}(aq) &-> 2CrO4^2- (aq) + \cancel{8H^{+}} + \cancel{6e-} + 3Cl2(g) + 6H2O(l)} \\[4pt]
\ce{2Cr(OH)4^- (aq) + 4H^{+} + 6ClO^{-}(aq) &-> 2CrO4^2- (aq) + 3Cl2(g) + 6H2O(l)}
\end{align*} \]Step 8: If the reaction takes place in basic solution, add OH− ions to both sides to neutralize the H+ ions, then simplify (remembering that \(\ce{H+ + OH- \rightarrow H2O(l)}\)):
\[\begin{align*} \ce{2Cr(OH)4^- (aq) + 4H^{+} + \mathbf{4OH- } + 6ClO^{-}(aq) &-> 2CrO4^2- (aq) + 3Cl2(g) + 6H2O(l) + \mathbf{4OH- }} \\[4pt] \ce{2Cr(OH)4^- (aq) + \cancel{\mathbf{4H2O }} + 6ClO^{-}(aq) &-> 2CrO4^2- (aq) + 3Cl2(g) + \mathbf{2}\cancel{6}H2O(l) + 4OH- } \\ \ce{2Cr(OH)4^- (aq) + 6ClO^{-}(aq) &-> 2CrO4^2- (aq) + 3Cl2(g) + 2H2O(l) + 4OH- }
\end{align*} \]Final Check
Element Reactants Products Cr 2 2 O 14 14 H 8 8 Cl 6 6 Total Charge:
Reactants: -2 + -6 = -8 Products: -4 + 0 + 0 + -4 = -8
Both atoms and total charge are balanced.
Galvanic Cells

Consider the diagram of the galvanic cell:
Identify the following:
a) Anode
b) Cathode
c) Salt bridge
d) Electrode with a negative charge
- Answer
-
a) The anode is the electrode where oxidation occurs and the electrons leave the electrode: A.
b) The cathode is the electrode where reduction occurs (gaining electrons): E.
c) The salt bridge is the U-shaped tube that allows ion flow to maintain charge balance between the half-cells: C.
d) The anode has a negative charge because it is the source of electrons in the external circuit: A.

Consider the diagram of the galvanic cell:
a) What metal makes up the anode?
b) What metal makes up the cathode?
c) Which electrode has a positive charge?
d) Which electrode loses mass as the cell operates?
e) Write the two half-reactions that occur in this galvanic cell. What is the overall balanced cell reaction?
f) Write the shorthand notation for this galvanic cell.
g) Which electrode could be replaced with an inactive material, such as platinum?
- Answer
-
a) Since electrons are leaving the Pb electrode, it is the anode where oxidation occurs.
b) Cu gains the electrons, so it is the cathode.
c) The cathode (Cu electrode) has a positive charge.
d) As the cell operates, the lead electrode is oxidized and loses mass into solution, \(\ce{Pb(s) \rightarrow Pb^2+ (aq) + 2e- }\).
e) Anode (oxidation): \(\ce{Pb(s) \rightarrow Pb^2+ (aq) + 2e- }\)
Cathode (reduction): \(\ce{Cu^2+ (aq) + 2e- \rightarrow Cu(s)}\)
Overall: \(\ce{Pb(s) + Cu^2+ (aq) \rightarrow Pb^2+ (aq) + Cu(s)}\)
f) \(\ce{Pb(s) ∣ Pb^2+ (aq) ∣∣ Cu^2+ (aq) ∣ Cu(s)}\)
g) The copper electrode could be replaced with Pt, since Cu is not oxidized in this galvanic cell.
A galvanic cell is constructed using a \(\ce{Ag/Ag+}\) half-cell and a \(\ce{Cu/Cu^2+ }\) half-cell. The copper electrode is negative.
a) Write the oxidation half-reaction, the reduction half-reaction, and the overall balanced redox reaction for this galvanic cell.
b) Draw and label the galvanic cell, indicating:
- the anode and cathode,
- the charge on each electrode,
- the direction of electron flow in the external circuit,
- the salt bridge, containing \(\ce{KNO3}\) and the direction of ion flow.
- Answer
-
a) Since the copper electrode is negative, it is the anode where oxidation occurs:
Anode (oxidation): \(\ce{Cu(s) \rightarrow Cu^2+ (aq) + 2e- }\)
Cathode (reduction): \(\ce{Ag^+ (aq) + e- \rightarrow Ag(s)}\)
Overall: \(\ce{Cu(s) + 2Ag+ (aq) \rightarrow Cu^2+ (aq) + 2Ag(s) }\)
b)

Write cell shorthand notations for the following cell reactions, using platinum as an inert electrode as needed.
a) \(\ce{Mg(s) + Ni^2+ (aq) \rightarrow Mg^2+ (aq) + Ni (s)}\)
b) \(\ce{2Ag+ (aq) + Cu(s) \rightarrow Cu^2+ (aq) + 2Ag(s)}\)
c) \(\ce{Mn(s) + Sn^2+ (aq) \rightarrow Mn^2+ (aq) + Sn(s)}\)
d. \(\ce{3Cu+ (aq) + Au^3+ \rightarrow 3Cu^2+ (aq) + Au(s)}\)
- Answer
-
The shorthand notation lists the anode on the left and the cathode on the right, with electrodes on the outside. Phases are separated by a single vertical line (∣∣), and the two half-cells are separated by a double line (∣∣).
If all species are in solution in a half-cell, a platinum electrode is used.
a) \(\ce{Mg(s)│ Mg^2+ (aq)║ Ni^2+ (aq)│Ni(s) }\)
b) \(\ce{Cu(s)│Cu^2+ (aq) ║Ag^+ (aq)│Ag(s) }\)
c) \(\ce{Mn(s) │Mn^2+ (aq) ║ Sn^2+ (aq)│Sn(s) }\)
d) Since both \(\ce{Cu+}\) and \(\ce{Cu^2+}\) are in solution in the anode compartment, a platinum electrode is required:
\(\ce{Pt(s) │Cu+ (aq), Cu^2+ (aq) ║ Au^3+ (aq)│Au(s) }\)
Why is a salt bridge necessary in galvanic cells?
- Answer
-
Without a salt bridge, the circuit would be incomplete, and no current could flow between the two half-cells. As the redox reaction proceeds, charge buildup would occur in each half-cell (excess positive in the oxidation half-cell, excess negative in the reduction half-cell), stopping the flow of electrons through the external circuit.
The salt bridge allows ions to flow between the half-cells to maintain electrical neutrality, completing the circuit and allowing electrons to continue flowing through the wire so the redox reaction (and current) can continue.
Standard Reduction Potentials (\(E_{cell}^\circ \))
What does the standard cell potential (\(E_{cell}^\circ \)) tell us about a galvanic cell and the redox reaction occurring within it?
- Answer
-
The standard cell potential (\(E_{cell}^\circ \)) indicates the driving force for the redox reaction under standard conditions (1 M concentrations, 1 atm pressure, 25°C):
If \(E_{cell}^\circ \) > 0, the redox reaction is spontaneous as written, and the galvanic cell can produce electrical energy. If \(E_{cell}^\circ \) < 0, the redox reaction is non-spontaneous as written, and the reverse reaction would be spontaneous.
The larger the positive value of \(E_{cell}^\circ \), the greater the tendency for the redox reaction to occur spontaneously, meaning the cell can produce a higher voltage.
In essence, \(E_{cell}^\circ \) helps us predict whether a redox reaction will proceed spontaneously and how much electrical energy can be harnessed from it under standard conditions.
For each of the following reactions:
- Identify which half-reaction occurs at the cathode and which occurs at the anode.
- Balance the overall redox reaction if needed.
- Calculate the standard cell potential (\(E_{cell}^\circ \)) for the reaction.
a) \(\ce{Fe^3+ (aq) + Zn(s) \rightarrow Fe^2+ (aq) + Zn^2+ (aq)}\)
b) \(\ce{Cu^2+ (aq) + Zn(s) \rightarrow Cu(s) + Zn^2+ (aq)}\)
c) \(\ce{Cd(s) + Cu^2+ (aq) \rightarrow Cd^2+ (aq) + Cu(s)}\)
d) \(\ce{Fe^2+ (aq) + Cl2 (g) \rightarrow Fe^3+ (aq) + 2Cl- (aq)}\)
Standard reduction potentials can be found in Table 11.3.1.
- Answer
-
Step 1: Identify which half-reaction occurs at the cathode (reduction) and which at the anode (oxidation).
Step 2: Balance electrons if needed and write the balanced overall reaction.
Step 3: Use \(E_{cell}^{\circ} = E_{ox}^{\circ} + E_{red}^{\circ}\) to calculate the standard cell potential.
a) reduction (cathode):\(\ce{Fe^3+ (aq) + e- \rightarrow Fe^2+ (aq)} \quad E_{red}^{\circ} = 0.77 \ \text{V} \)
oxidation (anode):\(\ce{Zn(s) \rightarrow Zn^2+ (aq) + 2e- } \quad E_{ox}^{\circ}=-E_{red}^{\circ}=+0.76 \ \text{V}\)
To balance the electrons, the reduction reaction must be multiplied by two.
Overall: \(\ce{2Fe^3+ (aq) + Zn(s) \rightarrow 2Fe^2+ (aq) + Zn^2+ (aq) }\)
\(E_{cell}^{\circ} = 0.77 \ \text{V} + 0.76 \ \text{V} = 1.53 \ \text{V} \)
The large, positive (\(E_{cell}^\circ \)) indicates the reaction is spontaneous under standard conditions, and the cell would function well as a galvanic cell.
b) reduction (cathode):\(\ce{Cu^2+ (aq) + 2e- \rightarrow Cu (s)} \quad E_{red}^{\circ} = 0.34 \ \text{V} \)
oxidation (anode):\(\ce{Zn(s) \rightarrow Zn^2+ (aq) + 2e- } \quad E_{ox}^{\circ}=-E_{red}^{\circ}=+0.76 \ \text{V}\)
Overall: \(\ce{Cu^2+ (aq) + Zn(s) \rightarrow Cu (s) + Zn^2+ (aq) }\)
\(E_{cell}^{\circ} = 0.34 \ \text{V} + 0.76 \ \text{V} = 1.10 \ \text{V} \)
The positive (\(E_{cell}^\circ \)) indicates the reaction is spontaneous under standard conditions, and the cell would function well as a galvanic cell.
c) reduction (cathode):\(\ce{Cu^2+ (aq) + 2e- \rightarrow Cu (s)} \quad E_{red}^{\circ} = 0.34 \ \text{V} \)
oxidation (anode):\(\ce{Cd(s) \rightarrow Cd^2+ (aq) + 2e- } \quad E_{ox}^{\circ}=-E_{red}^{\circ}=+0.40 \ \text{V}\)
Overall: \(\ce{Cu^2+ (aq) + Cd(s) \rightarrow Cu (s) + Cd^2+ (aq) }\)
\(E_{cell}^{\circ} = 0.34 \ \text{V} + 0.40 \ \text{V} = 0.74 \ \text{V} \)
The positive (\(E_{cell}^\circ \)) indicates the reaction is spontaneous under standard conditions, and the cell would function well as a galvanic cell.
d) reduction (cathode): \(\ce{Cl2 (g) + 2e- \rightarrow 2Cl- (aq)} E_{red}^{\circ} = 1.36 \ \text{V}\)
oxidation (anode): \(\ce{Fe^2+ (aq) \rightarrow Fe^3+ (aq) + e- (aq)} \quad E_{ox}^{\circ}=-E_{red}^{\circ}=-0.77 \ \text{V}\)
To balance the electrons, the oxidation reaction must be multiplied by two.
Overall: \(\ce{2Fe^2+ (aq) + Cl2 (g) \rightarrow 2Fe^3+ (aq) + 2Cl- (aq) }\)
\(E_{cell}^{\circ} = 1.36 \ \text{V} + -0.77 \ \text{V} = 0.59 \ \text{V} \)
The positive (\(E_{cell}^\circ \)) indicates the reaction is spontaneous under standard conditions, and the cell would function well as a galvanic cell.
Balance the following redox reaction under acidic conditions:
\[\ce{Mn^2+ (aq) + Cl2 (g) \rightarrow MnO4^- (aq) + 2Cl- (aq)} \nonumber\]
Is the reaction spontaneous under standard state conditions?
Standard reduction potentials can be found in Table 11.3.1.
- Answer
-
Step 1: Write skeletal equations for the oxidation and reduction half-reactions.
\[\begin{align*}
&\text { oxidation: } \quad \ce{Mn^2+ (aq) -> MnO4^- (aq) } \\[4pt]
&\text { reduction: } \quad \ce{Cl2 (g) \rightarrow 2Cl- (aq)}\end{align*} \nonumber \]Step 2: Balance each half-reaction for all elements except \(\ce{H}\) and \(\ce{O}\). Complete!
Step 3: Balance each half-reaction for \(\ce{\mathbf{O}}\) by adding \(\ce{\mathbf{H2O}}\):
\[\begin{align*}
&\text { oxidation: } \quad \ce{4H2O(l) + Mn^2+ (aq) -> MnO4^- (aq) } \\[4pt]
&\text { reduction: } \quad \ce{Cl2 (g) \rightarrow 2Cl- (aq)}\end{align*} \nonumber \]Step 4: Balance each half-reaction for \(\ce{\mathbf{H}}\) by adding \(\ce{\mathbf{H^{+}}}\):
\[\begin{align*}
&\text { oxidation: } \quad \ce{4H2O(l) + Mn^2+ (aq) -> MnO4^- (aq) + 8H+ (aq)} \\[4pt]
&\text { reduction: } \quad \ce{Cl2 (g) \rightarrow 2Cl- (aq)}\end{align*} \]Step 5: Balance each half-reaction for charge by adding electrons:
\[\begin{align*}
&\text { oxidation: } \quad \ce{4H2O(l) + Mn^2+ (aq) -> MnO4^- (aq) + 8H+ (aq) + 5e- } \\[4pt]
&\text { reduction: } \quad \ce{Cl2 (g) + 2e- \rightarrow 2Cl- (aq)}\end{align*} \]Step 6: If necessary, multiply one or both half-reactions so that the number of electrons gained equals the number lost:
\[\begin{align*}
&\text { oxidation: }(\times 2) \quad \ce{8H2O(l) + 2Mn^2+ (aq) -> 2MnO4^- (aq) + 16H+ (aq) + 10e- } \\[4pt]
&\text { reduction: }(\times 5) \quad \ce{5Cl2 (g) + 10e- \rightarrow 10Cl- (aq)}\end{align*} \nonumber \]Step 7: Add the two half-reactions and simplify:
\[\begin{align*}
\ce{8H2O(l) + 2Mn^2+ (aq) + 5Cl2 (g) + \cancel{10e- } &-> 2MnO4^- (aq) + 16H+ (aq) + \cancel{10e- } + 10Cl- (aq)} \\[4pt]
\ce{8H2O(l) + 2Mn^2+ (aq) + 5Cl2 (g) &-> 2MnO4^- (aq) + 16H+ (aq) + 10Cl- (aq)}\end{align*} \nonumber \]A good final check is to verify that both atom counts and total charge are balanced:
H: 16 ✓, O: 8 ✓, Mn: 2 ✓, Cl: 10 ✓ Charges: 4+ each side ✓
\(E_{cell}^{\circ} = E_{ox}^{\circ} + E_{red}^{\circ}=-1.51 \ \text{V} + 1.36 \ \text{V} = -0.15 \ \text{V}\)
Since the standard cell potential is negative, the redox reaction is nonspontaneous under standard state conditions.
Consider the following reduction potentials:
\(\ce{Ca^{2+}(aq) + 2e^- -> Ca(s)} \quad E_{red}^{\circ} = -2.87 \, V\)
\(\ce{Cd^{2+}(aq) + 2e^- -> Cd(s)} \quad E_{red}^{\circ} = -0.40 \, V\)
\(\ce{Fe^{3+}(aq) + e^- -> Fe^{2+}(aq)} \quad E_{red}^{\circ} = +0.77 \, V\)
\(\ce{Ag^{+}(aq) + e^- -> Ag(s)} \quad E_{red}^{\circ} = +0.80 \, V\)
Which of these species is the strongest oxidizing agent? Which species is the strongest reducing agent?
- Answer
-
Strongest oxidizing agent:
The species with the highest (most positive) \(E_{red}^{\circ}\) will most readily gain electrons: \(\ce{Ag+}\).Strongest reducing agent: The reducing agent is being oxidized, so we need to consider the oxidation reactions, the reverse of the reduction reactions. The species with the lowest (most negative) \(E_{red}^{\circ}\) will most readily lose electrons (as its oxidation potential is highest): \(\ce{Ca(s)}\).
Consider the following reduction potentials:
\(\ce{S2O8^2- (aq) + 2e- -> 2SO4^2- (aq)}\quad E_{red}^{\circ} = 2.01 \, V\)
\(\ce{Sn^{2+}(aq) + 2e^- -> Sn(s)} \quad E_{red}^{\circ} = -0.14 \, V\)
\(\ce{Fe^{2+}(aq) + 2e^- -> Fe(s)} \quad E_{red}^{\circ} = -0.45 \, V\)
a) Which species is the strongest oxidizing agent? Which species is the strongest reducing agent?
b) Using these half-reactions, write three spontaneous redox reactions (under standard state conditions) and calculate (\(E_{cell}^\circ \)) for each.
- Answer
-
a) Strongest oxidizing agent:
The species with the highest (most positive) \(E_{red}^{\circ}\) will most readily gain electrons: \(\ce{S2O8^2- (aq)}\).Strongest reducing agent: The reducing agent is being oxidized, so we need to consider the oxidation reactions, the reverse of the reduction reactions. The species with the lowest (most negative) \(E_{red}^{\circ}\) will most readily lose electrons (as its oxidation potential is highest): \(\ce{Fe(s)}\).
b) To write redox reactions, we need one reduction half-reaction and one oxidation half-reaction. To give a spontaneous reaction, we need a positive value of (\(E_{cell}^\circ \)).
Reaction 1:
To get the highest possible (\(E_{cell}^\circ \)), we would take the largest reduction potential and the smallest (most negative) reduction potential, which we will reverse to give the oxidation half reaction:
reduction: \(\ce{S2O8^2- (aq) + 2e- -> 2SO4^2- (aq)}\quad E_{red}^{\circ} = 2.01 \, V\)
oxidation: \(\ce{Fe(s) -> Fe^{2+}(aq) + 2e^-} \quad E_{ox}^{\circ} =-E_{red}^{\circ} = +0.45 \, V\)
overall: \(\ce{S2O8^2- (aq) + Fe(s) -> 2SO4^2- (aq) + Fe^2+ (aq)}\)
\(E_{cell}^{\circ} = E_{ox}^{\circ} + E_{red}^{\circ}=0.45 \ \text{V} + 2.01 \ \text{V} = 2.46 \ \text{V}\)
Reaction 2:
reduction: \(\ce{S2O8^2- (aq) + 2e- -> 2SO4^2- (aq)}\quad E_{red}^{\circ} = 2.01 \, V\)
oxidation: \(\ce{Sn(s) -> Sn^{2+}(aq) + 2e^-} \quad E_{ox}^{\circ} =-E_{red}^{\circ} = +0.14 \, V\)
overall: \(\ce{S2O8^2- (aq) + Sn(s) -> 2SO4^2- (aq) + Sn^2+ (aq)}\)
\(E_{cell}^{\circ} = E_{ox}^{\circ} + E_{red}^{\circ}=0.14 \ \text{V} + 2.01 \ \text{V} = 2.15 \ \text{V}\)
Reaction 3:
reduction: \(\ce{Sn^{2+}(aq) + 2e^- -> Sn(s)} \quad E_{red}^{\circ} = -0.14 \, V\)
oxidation: \(\ce{Fe(s) -> Fe^{2+}(aq) + 2e^-} \quad E_{ox}^{\circ} =-E_{red}^{\circ} = +0.45 \, V\)
overall: \(\ce{Sn^{2+}(aq) + Fe(s) -> Sn(s) + Fe^2+ (aq)}\)
\(E_{cell}^{\circ} = E_{ox}^{\circ} + E_{red}^{\circ}=0.45 \ \text{V} + -0.14 \ \text{V} = 0.31 \ \text{V}\)
Cell Potentials, Free Energy, and Equilibrium
Calculate \(\Delta G^\circ \) for the reactions below.
a) \(\ce{Cu(s) + Sn^4+ (aq) \rightarrow Cu^2+(aq) + Sn^2+(aq)}\)
b) \(\ce{2Cl_2(g) + 2H_2O(l) \rightarrow O_2(g) + 4H^+(aq) + 4Cl^{-}(aq)}\)
Standard reduction potentials can be found in Table 11.3.1.
- Answer
-
a) Oxidation: \(\ce{Cu(s) \rightarrow Cu^2+(aq) + 2e^{-}} \hspace{55 pt}\quad {E}_{ox}^\circ=-0.34\:V\)
Reduction: \(\ce{Sn^4+(aq) + 2e^- \rightarrow Sn^2+(aq)} \hspace{55 pt}\quad {E}_{red}^\circ=0.15\:V\)
\(E_{cell}^{\circ}=E_{ox}^{\circ} + E_{red}^{\circ}=-0.34\:V + 0.15\:V=-0.19\:V\)
Since \(E_{cell}^{\circ}\) is negative, \(\Delta G^\circ\) must be positive:
\(\Delta G^\circ=-nFE^\circ_{cell}=-2(96485\: C/mol)(-0.19\:J/C)= 36664\: J/mol= 37\: kJ/mol\)
The reaction is non-spontaneous under standard state conditions.
b) Oxidation: \(\ce{2H_2O(l) \rightarrow O_2(g) + 4H^+(aq) + 4e^-}\hspace{55 pt} \ {E}_{ox}^\circ=-1.23\:V\)
Reduction: \(\ce{2Cl2 (g) +4e^- \rightarrow 4Cl- (aq)}\hspace{55 pt}\quad \quad {E}_{red}^\circ=1.36\:V\)
\(E_{cell}^{\circ}=E_{ox}^{\circ} + E_{red}^{\circ}=-1.23\:V + 1.36\:V=0.13\:V\)
Since \(E_{cell}^{\circ}\) is positive, \(\Delta G^\circ\) must be negative:
\(\Delta G^\circ=-nFE^\circ_{cell}=-4(96485\: C/mol)(0.13\:J/C)= -50172\: J/mol= -50\: kJ/mol\)
The reaction is spontaneous under standard state conditions.
Calculate the equilibrium constant (\(K\)) for the following reactions.
- \(\ce{Ca^2+(aq) + 2Li(s) \rightleftharpoons Ca(s) + 2Li+(aq)}\)
- \(\ce{Cu^2+(aq) + Ni(OH)2 (s) + 2OH- (aq) \rightleftharpoons Cu(s) + NiO2(s) + 2H2O(l)}\)
Standard reduction potentials can be found in Table 11.3.1.
- Answer
-
a) Reaction: \(\ce{Ca^{2+}(aq) + 2Li(s) \rightleftharpoons Ca(s) + 2Li^{+}(aq)}\)
Half-reactions:
Reduction: \(\ce{Ca^{2+}(aq) + 2e^- \rightleftharpoons Ca(s)} \quad E^{\circ}_{red} = -2.87 \, V\)
Oxidation: \(\ce{2Li(s) \rightleftharpoons 2Li^{+}(aq) + 2e^-} \quad E^{\circ}_{ox} = 3.04 \, V\)
\[ E_{cell}^{\circ} = E_{ox}^{\circ} + E_{red}^{\circ} = 3.04 \, V + (-2.87 \, V) = 0.17 \, V \nonumber\]
Calculate \(K\):
\[ E_{cell}^{\circ} = \frac{RT}{nF} \ln K \quad \rightarrow \quad \ln K = \frac{nFE_{cell}^{\circ}}{RT} \nonumber\]
Using \(n = 2\), \(F = 96485 \, C/mol\), \(R = 8.314 \, J/(mol \cdot K)\), and \(T = 298 \, K\):
\[ \ln K = \frac{(2)(96485)(0.17)}{8.314 \times 298} = 13.24 \nonumber\] \[ K = e^{13.24} = 5.6 \times 10^{5} \nonumber\]
This large \(K\) indicates the reaction is strongly product-favoured.
b) Reaction: \(\ce{Cu^{2+}(aq) + Ni(OH)_2(s) + 2OH^{-}(aq) \rightleftharpoons Cu(s) + NiO_2(s) + 2H_2O(l)}\)
Half-reactions:
Reduction: \(\ce{Cu^{2+}(aq) + 2e^- \rightleftharpoons Cu(s)} \quad E^{\circ}_{red} = 0.34 \, V\)
Oxidation: \(\ce{Ni(OH)_2(s) + 2OH^{-}(aq) \rightleftharpoons NiO_2(s) + 2H_2O(l) + 2e^-} \quad E^{\circ}_{ox} = -0.49 \, V\)
\[ E_{cell}^{\circ} = E_{ox}^{\circ} + E_{red}^{\circ} = -0.49 \, V + 0.34 \, V = -0.15 \, V \nonumber\]
Calculate \(K\):
\[ \ln K = \frac{(2)(96485)(-0.15)}{8.314 \times 298} = -11.68 \nonumber\] \[ K = e^{-11.68} = 8.5 \times 10^{-6} \nonumber\]
This very small \(K\) indicates the reaction is strongly reactant-favoured.
At 298 K, the following reaction has an equilibrium constant of 2.32 x 1027.
\(\ce{6Br- (aq) + 14H+ (aq) + Cr2O7^2- (aq) \rightleftharpoons 2 Cr^3+ (aq) + 3 Br2 (l) + 7 H2O (l)}\)
What is the standard cell potential for the reaction? What is the standard free energy change?
- Answer
-
To find K, we need to know how many electrons are transferred in the reaction:
In \(\ce{Br-}\), the oxidation number of Br is -1. In \(\ce{Br2}\), the oxidation number is 0. Each Br loses 1 electron, so a total of 6 electrons are transferred in the redox reaction.
Similarly, in \(\ce{Cr2O7^2-}\), the oxidation number of Cr is +6. In \(\ce{Cr^3+}\), the oxidation number is +3. Each Cr gains 3 electrons, so a total of 6 electrons.
\[
\begin{align*}
E_{cell}^{\circ} &= \frac{RT}{nF} \ln K \\[6pt]
&= \frac{(8.314 \, \text{J mol}^{-1} \text{K}^{-1})(298 \, \text{K})}{(6)(96485 \, \text{C mol}^{-1})} \ln (2.32 \times 10^{27}) \\[6pt]
&= 0.270 \, \text{V}
\end{align*}
\]\(\Delta G^\circ=-nFE^\circ_{cell}=-6(96485\: \text{C/mol})(0.270 \ \text{J/C})= -1.56 \times 10^5\: \text{J/mol}=-156 \: \text{kJ/mol}\)
The reaction is spontaneous under standard state conditions. This is confirmed by the positive value of \(E_{cell}^{\circ}\) and the negative value of \(\Delta G^\circ\).
Cell Potentials Beyond Standard Conditions
Consider the following reaction taking place in a galvanic cell at 298 K:
\(\ce{Cu^2+ (aq) + Zn(s) \rightarrow Cu(s) + Zn^2+ (aq)}\)
reduction (cathode):\(\ce{Cu^2+ (aq) + 2e- \rightarrow Cu (s)} \quad E_{red}^{\circ} = 0.34 \ \text{V} \)
oxidation (anode):\(\ce{Zn(s) \rightarrow Zn^2+ (aq) + 2e- } \quad E_{ox}^{\circ}=0.76 \ \text{V}\)
a) What is the standard cell potential (\(E_{cell}^{\circ}\))?
b) What is the cell potential (\(E_{cell}\)) when [\(\ce{Cu^2+}\)] = 1.5 M and [\(\ce{Zn^2+}\)]= 0.10 M? (Before performing the calculation, would you expect the cell potential to be greater or less than the standard cell potential?)
c) What is the cell potential (\(E_{cell}\)) when [\(\ce{Cu^2+}\)] = 0.50 M and [\(\ce{Zn^2+}\)]= 1.5 M? (Before performing the calculation, would you expect the cell potential to be greater or less than the standard cell potential?)
- Answer
-
a) \(E_{cell}^{\circ} = 0.34 \, \text{V} + 0.76 \, \text{V} = 1.10 \, \text{V}\)
b) \[Q = \frac{[\ce{Zn^2+}]}{[\ce{Cu^2+ }]}\nonumber\]
\[ E_{cell} = E^\circ_{cell} - \frac{RT}{nF} \ln Q \nonumber\]
\[ E_{cell} = E^\circ_{cell} - \frac{RT}{nF} \ln \frac{[\ce{Zn^2+}]}{[\ce{Cu^2+ }]} \nonumber\]
Since the concentration of the reactant (\(\ce{Cu^2+ }\)) is higher and the concentration of the product (\(\ce{Zn^2+ }\)) is lower than under standard conditions, the cell is further from equilibrium, so the cell potential should be greater than the standard cell potential.
\[ E_{cell} = 1.10 \ \text{V} - \frac{(8.314 \frac{\text{J}}{\text{mol} \cdot \text{K}})(298\ \text{K})}{2(96485 \, \text{C/mol})} \ln \frac{(0.10)}{(1.5)} =1.13\ \text{V}\nonumber\]
As predicted, the cell potential is greater than the standard cell potential.
c) Since the concentration of the reactant (\(\ce{Cu^2+ }\)) is lower and the concentration of the product (\(\ce{Zn^2+ }\)) is higher than under standard conditions, the cell potential should be lower than the standard cell potential.
\[ E_{cell} = 1.10 \ \text{V} - \frac{(8.314 \frac{\text{J}}{\text{mol} \cdot \text{K}})(298\ \text{K})}{2(96485 \, \text{C/mol})} \ln \frac{(1.5)}{(0.50)} =1.09\ \text{V}\nonumber\]
As predicted, the cell potential is lower than the standard cell potential.
The following galvanic cell has a cell potential (\(E_{cell}\)) of 1.54 V. What is the concentration of \(\ce{Ag+}\) in the cell?
\(\ce{Zn(s) | Zn^{2+}} (2.00\: \text{M}) \ce{|| Ag^+(?\:M) | Ag(s)}\)
Standard reduction potentials:
\(\ce{Zn^{2+}(aq) + 2e^- \rightleftharpoons Zn(s)} \quad E_{red}^\circ= -0.76\: V\)
\(\ce{Ag^+(aq) + e^- \rightleftharpoons Ag(s) } \quad E_{red}^\circ= 0.80\: V\)
- Answer
-
From the cell notation, \(\ce{Zn(s)}\) is at the anode (left), meaning it is oxidized. \(\ce{Ag+ }\) is at the cathode (right), so it is reduced.
This also agrees with standard reduction potentials: \(\ce{Ag+ }\) has a higher reduction potential than \(\ce{Zn^2+ }\), so silver ions are reduced and zinc metal is oxidized.
Oxidation: \(\ce{Zn(s) \rightleftharpoons Zn^{2+} (aq) + 2e^- }\quad E_{ox}^\circ= +0.76\: V\)
Reduction: \(\ce{2Ag^+(aq) + 2e^- \rightleftharpoons 2Ag(s)} \quad E_{red}^\circ= 0.80\: V\)Net Reaction: \(\ce{Zn(s) + 2Ag^+ (aq) \rightleftharpoons Zn^{2+}(aq) + 2Ag(s)} \quad E^\circ_{cell}= 1.56\: V\)
Use Nernst equation to calculate \(\ce{[Ag+]}\):\[ E_{cell} = E^\circ_{cell} - \frac{RT}{nF} \ln Q \nonumber\]
\[1.54 \, V = 1.56 \, V - \frac{8.314 \frac{J}{mol \cdot K}(298 \, K)}{2(96485 \, C/mol)} \ln Q \nonumber\]
\[\ln Q = 1.5577 \nonumber\]
\[Q = \frac{[\ce{Zn^2+}]}{[\ce{Ag^+}]^2}=\frac{2.00}{[\ce{Ag^+}]^2}=4.748\nonumber\]
\[[\ce{Ag+}]=0.6 \ M\nonumber\]
What is the cell potential (\(E_{cell}\)) for the following galvanic cell?
\(\ce{Co(s) | Co^{2+}} (0.6\: \text{M}) \ce{|| Fe^{3+}} (1.0\: \text{M}), \ce{Fe^{2+}} (0.9\: \text{M}) \ce{| Pt(s)}\)
Standard reduction potentials:
\(\ce{Co^{2+}(aq) + 2e^- \rightleftharpoons Co(s)} \quad E_{red}^\circ= -0.28\: V\)
\(\ce{Fe^3+(aq) + e^- \rightleftharpoons Fe^2+(aq)} \quad E_{red}^\circ= 0.77\: V\)
- Answer
-
From the cell notation, \(\ce{Co(s)}\) is at the anode (left), meaning it is oxidized. \(\ce{Fe^3+ }\) is reduced (right).
This also agrees with standard reduction potentials: \(\ce{Fe^3+ }\) has a higher reduction potential than \(\ce{Co^2+ }\), so \(\ce{Fe^3+ }\) is reduced and cobalt metal is oxidized.
\(\ce{2Fe^3+(aq) + Co(s) \rightleftharpoons 2Fe^2+(aq) + Co^{2+}(aq)}\)
Determine \(E^\circ_{cell}\).
\(E_{cell}^{\circ} = 0.28 \, V + 0.77 \, V = 1.05 \, V\)
\[Q = \frac{[\ce{Co^2+}][\ce{Fe^2+}]^2}{[\ce{Fe^3+ }]^2}=\frac{(0.6)(0.9)^2}{(1.0)^2}=0.486\nonumber\]
\[ E_{cell} = E^\circ_{cell} - \frac{RT}{nF} \ln Q \nonumber\]
\[ E_{cell} = 1.05 \, V - \frac{8.314 \frac{J}{mol \cdot K}(298 \, K)}{2(96485 \, C/mol)} \ln(0.486)=1.06 \, V \nonumber\]
What is the cell potential (\(E_{cell}\)) for the following concentration cell?
![A copper concentration cell: Left half-cell (anode): [\(\ce{Cu2+}]=0.010 M, Right half-cell (cathode): [\(\ce{Cu2+}\)]=0.10 M Copper electrodes, KNO₃ salt bridge, and lightbulb indicating current flows.](https://chem.libretexts.org/@api/deki/files/489265/clipboard_efa07e74c0842d12b4284dc5c90026d4a.png?revision=1&size=bestfit&width=479&height=386)
- Answer
-
Since both half-cells use the \(\ce{Cu^2+/Cu}\) couple, the standard cell potential is 0 V. However, the cell generates a voltage because the concentrations of \(\ce{Cu^2+}\) are different in the two half-cells.
Oxidation occurs in the less concentrated solution (0.010 M), while reduction occurs in the more concentrated solution (0.10 M), as the cell spontaneously works to equalize concentrations.
The overall process is:
\( \ce{Cu^2+} (aq, 0.10 M) \rightarrow \ce{Cu^2+} (aq, 0.010 M) \\ \quad Q = \frac{[\ce{Cu^2+ }]_{dilute}}{[\ce{Cu^2+ }]_{conc}} = \frac{0.010}{0.10}=0.10\)
Each \(\ce{Cu^2+/Cu}\) half-reaction involves two electrons transferred per copper ion:
\(\ce{Cu^2+(aq) + 2e- → Cu(s)}\)Even though the electrodes are identical, the electron transfer through the external circuit still involves 2 electrons per \(\ce{Cu^2+ }\) ion reduced or oxidized, so we use n = 2 in the Nernst equation.
\[ E_{cell} = 0 \, V - \frac{8.314 \frac{J}{mol \cdot K}(298K)}{2(96485 \, C/mol)} \ln(0.10)=0.030 \, V \nonumber\]
The positive cell potential confirms that the spontaneous direction is from the more concentrated to the less concentrated half-cell.
For the following redox reaction:
\(\ce{Co(s) + Ni^2+ (aq) \rightleftharpoons Ni(s) + Co^2+ (aq)}\)
When [\(\ce{Ni^2+}\)] = 0.20 M and [\(\ce{Co^2+}\)] = 0.010 M,
a) What is the cell potential at these concentrations? In which direction does the reaction proceed spontaneously?
b) What are the concentrations of the metal ions when the battery is dead?
Standard reduction potentials:
\(\ce{Co^{2+}(aq) + 2e^- \rightleftharpoons Co(s)} \quad E_{red}^\circ= -0.280\: V\)
\(\ce{Ni^{2+}(aq) + 2e^- \rightleftharpoons Ni(s)} \quad E_{red}^\circ= -0.260\: V\)
- Answer
-
\(E_{cell}^{\circ} = 0.28 \, V - 0.26 \, V = 0.020 \, V\)
a) \[Q = \frac{[\ce{Co^2+}]}{[\ce{Ni^2+}]}=\frac{(0.010)}{(0.20)}=0.050\nonumber\]
\[ E_{cell} = E^\circ_{cell} - \frac{RT}{nF} \ln Q \nonumber\]
\[ E_{cell} = 0.020 \, V - \frac{8.314 \frac{J}{mol \cdot K}(298 \, K)}{2(96485 \, C/mol)} \ln(0.050)=0.058 \, V \nonumber\]
The reaction will proceed in the forward direction
b) When the battery is dead, the redox reaction is at equilibrium. We can find the equilibrium concentration:
\[ E_{cell}^{\circ} = \frac{RT}{nF} \ln K \quad \rightarrow \quad \ln K = \frac{nFE_{cell}^{\circ}}{RT} \nonumber\]
\[ \ln K = \frac{(2)(96485 \, C/mol)(0.020 \, V)}{(8.314 \frac{J}{mol \cdot K})(298 \, K)} = 1.56 \nonumber\] \[ K = e^{1.56} = 4.7\nonumber\]
Co(s) +
Ni2+(aq) ⇌
Co2+(aq)
+ Ni(s)
Initial
-
0.20 M
0.010 M
-
Change
-
-x
+x
-
Equilibrium
-
0.20 - x
0.010 + x
-
\[K = \frac{[\ce{Co^2+}]}{[\ce{Ni^2+}]}=\frac{(0.010+x)}{(0.20-x)}=4.7 \\
0.010+x = 0.94 -4.7x \\
x = 0.16 \, M\nonumber\]Equilibrium concentrations: [\(\ce{Ni^2+}\)] = 0.04 M and [\(\ce{Co^2+}\)] = 0.17 M.
Corrosion
Which member of each pair of metals is more likely to corrode (oxidize)?
a) Mg or Ca b) Au or Pb c) Fe or Zn d) Ag or Pt
Use the table of standard reduction potentials:
| Metal | Reduction Half-Reaction | \(E^\circ_{\text{red}}\) (V) |
|---|---|---|
| Gold (\(\ce{Au}\)) | \(\ce{Au^{3+}(aq) + 3e^{-} -> Au(s)}\) | +1.50 |
| Platinum (\(\ce{Pt}\)) | \(\ce{Pt^{2+}(aq) + 2e^{-} -> Pt(s)}\) | +1.20 |
| Silver (\(\ce{Ag}\)) | \(\ce{Ag^{+}(aq) + e^{-} -> Ag(s)}\) | +0.80 |
| Lead (\(\ce{Pb}\)) | \(\ce{Pb^{2+}(aq) + 2e^{-} -> Pb(s)}\) | -0.13 |
| Iron (\(\ce{Fe}\)) | \(\ce{Fe^{2+}(aq) + 2e^{-} -> Fe(s)}\) | -0.45 |
| Zinc (\(\ce{Zn}\)) | \(\ce{Zn^{2+}(aq) + 2e^{-} -> Zn(s)}\) | -0.76 |
| Magnesium (\(\ce{Mg}\)) | \(\ce{Mg^{2+}(aq) + 2e^{-} -> Mg(s)}\) | -2.37 |
| Calcium (\(\ce{Ca}\)) | \(\ce{Ca^{2+}(aq) + 2e^{-} -> Ca(s)}\) | -2.87 |
- Answer
-
A lower (more negative) reduction potential means the metal ion is less easily reduced and the metal itself is more easily oxidized and more likely to corrode.
- Ca is more easily oxidized than Mg.
- Pb is more easily oxidized than Au.
- Zn is more easily oxidized than Fe.
- Ag is more easily oxidized than Pt.
Consider the following metals: Ag, Au, Mg, Ni, and Zn. Which of these metals could be used as a sacrificial anode in the cathodic protection of an underground steel storage tank?
Note: Steel is an alloy composed mostly of iron.
| Metal | Reduction Half-Reaction | \(E^\circ_{\text{red}}\) (V) |
|---|---|---|
| Gold (\(\ce{Au}\)) | \(\ce{Au^{3+}(aq) + 3e^{-} -> Au(s)}\) | +1.50 |
| Silver (\(\ce{Ag}\)) | \(\ce{Ag^{+}(aq) + e^{-} -> Ag(s)}\) | +0.80 |
| Nickel (\(\ce{Ni}\)) | \(\ce{Ni^{2+}(aq) + 2e^{-} -> Ni(s)}\) | -0.26 |
| Iron (\(\ce{Fe}\)) | \(\ce{Fe^{2+}(aq) + 2e^{-} -> Fe(s)}\) | -0.45 |
| Zinc (\(\ce{Zn}\)) | \(\ce{Zn^{2+}(aq) + 2e^{-} -> Zn(s)}\) | -0.76 |
| Magnesium (\(\ce{Mg}\)) | \(\ce{Mg^{2+}(aq) + 2e^{-} -> Mg(s)}\) | -2.37 |
- Answer
-
A sacrificial anode must be more easily oxidized than iron to protect it. A lower (more negative) reduction potential means the metal ion is less easily reduced and the metal itself is more easily oxidized than iron, allowing it to corrode preferentially and protect the steel.
Magnesium and zinc are suitable sacrificial anodes for the steel storage tank because the reduction potential of their ions is lower (more negative) than the reduction potential for \(\ce{Fe^2+}\).
Gold, silver, and nickel ions have higher (less negative) reduction potentials compared to \(\ce{Fe^2+}\), so gold, silver and nickel are less easily oxidized than iron. They will not serve as sacrificial anodes in this application.
Electrolysis
Aluminum metal is produced industrially by the electrolysis of molten \(\ce{AlCl3(l)}\). Write the half-reactions at the anode and cathode, calculate the standard cell potential, and explain why an external voltage is required for this process to occur.
Given standard reduction potentials:
- \(\ce{Al^{3+}(l) + 3e^- -> Al (l)}\) \(E^\circ_{\text{red}} = -1.66\,\text{V}\)
- \(\ce{Cl_2 (g) + 2e^- -> 2Cl^- (l)}\) \(E^\circ_{\text{red}} = +1.36\,\text{V}\)
- Answer
-
Cathode (reduction):
\[\ce{Al^{3+} (l) + 3e^- -> Al (l)} \quad E^\circ_{\text{red}} = -1.66\,\text{V} \nonumber\]Anode (oxidation):
Reverse the reduction of chlorine:
\[\ce{2Cl^- (l) -> Cl_2 (g) + 2e^-} \quad E^\circ_{\text{ox}} = -1.36\,\text{V} \nonumber\]Calculating \(E^\circ_{\text{cell}}\):
Using \( E^\circ_{\text{cell}} = E^\circ_{\text{ox}} + E^\circ_{\text{red}} \), we get:
\[ E^\circ_{\text{cell}} = (-1.36\,\text{V}) + (-1.66\,\text{V}) = -3.02\,\text{V} \nonumber\]
The negative cell potential shows the reaction is non-spontaneous under standard conditions and requires an external voltage greater than 3.02 V to drive the electrolysis of molten \(\ce{AlCl_3}\).
Industrial Context:
This process is used in the Hall-Héroult process for aluminum production, where molten \(\ce{Al_2O_3}\) dissolved in molten cryolite or molten \(\ce{AlCl_3}\) is electrolyzed to produce aluminum metal at the cathode and chlorine gas at the anode. The required high temperatures and external voltage make aluminum production energy-intensive.
In the industrial electrolysis of molten \(\ce{AlCl_3}\), a current of 25.0 A is passed through the electrolytic cell for 4.00 hours.
a) How many grams of aluminum metal are produced?
b) What volume of chlorine gas (at STP) is produced at the anode?
Given:
- Molar mass of Al = 26.98 g/mol
- Faraday’s constant = 96485 C/mol e–
- Molar volume at STP = 22.4 L/mol
- Answer
-
Calculate the total charge passed:
\[ Q = I \times t = (25.0 \, \text{C/s})(4.00 \, \text{h}) \left(\frac{60 \, \text{min}}{\text{h}} \right) \left(\frac{60 \, \text{s}}{\text{min}} \right) = 360000 \, \text{C} \nonumber\]
Calculate moles of electrons:
\[ n_{\text{e}^-} = \frac{Q}{F} = \frac{360000 \, \text{C}}{96485 \, \text{C/mol}} = 3.731 \, \text{mol e}^- \nonumber\]
a) Mass of aluminum produced:
Half-reaction: \(\ce{Al^{3+} + 3e^- -> Al (l)}\)
Mass of \(\ce{Al}\) produced:
\[3.731 \, \text{mol e}^- \left(\frac{1 \, \text{mol Al}}{3 \, \text{mol e}^-} \right)\left(\frac{26.98 \, \text{g}}{\text{mol}} \right) = 33.6 \, \text{g} \nonumber\]
b) Volume of \(\ce{Cl_2}\) produced
Anode half-reaction: \(\ce{2Cl^- -> Cl_2 (g) + 2e^-}\)
\[3.731 \, \text{mol e}^- \left(\frac{1 \, \text{mol Cl}_2}{2 \, \text{mol e}^-} \right)\left(\frac{22.4 \, \text{L}}{\text{mol}} \right) = 41.8 \, \text{L} \nonumber\]
A 12-V lead-acid car battery consists of 6 cells in series, each with the discharge reaction:
\[\ce{Pb(s) + PbO_2(s) + 2H_2SO_4(aq) -> 2PbSO_4(s) + 2H_2O(l)} \nonumber\]
When recharging, the battery is electrolyzed in the reverse direction. The relevant half-reactions during charging are:
At the cathode: \(\ce{Pb^{2+} (aq) + 2e^- -> Pb(s)}\)
At the anode: \(\ce{PbSO_4(s) + 2H_2O(l) -> PbO_2(s) + 4H^+ (aq) + SO_4^{2-} (aq) + 2e^-} \)
If a current of 4.50 A is used to charge the battery for 8.00 hours, what mass of lead (\(\ce{Pb}\)) is re-plated onto the cathode during recharging?
(Molar mass of Pb = 207.2 g/mol)
- Answer
-
Each mole of Pb requires 2 mol of electrons to plate.
Calculate the mass of Pb re-plated on the cathode using:
\[ \text{mass Pb} = (4.50\,\text{C/s})(8.00\,\text{h})(3600\,\text{s/h}) \times \frac{1\,\text{mol e}^-}{96485\,\text{C}} \times \frac{1\,\text{mol Pb}}{2\,\text{mol e}^-} \times 207.2\,\text{g/mol Pb} = 139\,\text{g} \nonumber\]
Additional Problems
You have a galvanic cell at 25°C constructed as follows:
\[\ce{Pt(s) | H2(g, 1 \, atm) | H^+(aq, ? \, M) || Ag^+} (\text{aq}, 1.0 \, \text{M}) \ce{| Ag(s)} \nonumber\]
The measured cell potential is \(E_{\text{cell}} = 1.01 \, \text{V}\).
Given:
\(\ce{2H^+(aq) + 2e^- ->H_2(g)} \quad E^\circ_{\text{red}} = 0.00 \, \text{V}\)
\(\ce{Ag^+(aq) + e^- -> Ag(s)} \quad E^\circ_{\text{red}} (\ce{Ag^+ / Ag}) = +0.80 \, \text{V}\)
Calculate the pH of the unknown acid solution.
- Answer
-
We can determine the overall reaction in two ways:
- From the cell notation, oxidation occurs at the left-hand electrode (\(\ce{Pt(s) ∣ H2 (g) ∣H+ (aq) }\)) and reduction occurs at the right-hand electrode (\(\ce{Ag+ (aq) ∣ Ag (s)}\)). This means hydrogen gas is oxidized and silver ions are reduced.
- From standard reduction potentials, \(\ce{Ag+ }\) has a higher reduction potential than \(\ce{H+}\), so silver ions will be reduced at the cathode, and hydrogen gas will be oxidized at the anode.
Therefore, the overall reaction is:
\(\ce{H2(g) + 2Ag+ (aq) \rightleftharpoons 2H+ (aq) + 2Ag(s)}\)
Calculate the standard cell potential:
\[ E^\circ_{\text{cell}} = E^\circ_{\text{ox}} + E^\circ_{\text{red}} = (0.00 \, \text{V}) + (0.80 \, \text{V}) = 0.80 \, \text{V} \nonumber\]
Apply the Nernst equation:
\[ E_{cell} = E^\circ_{cell} - \frac{RT}{nF} \ln Q \nonumber\]
\[1.01 \, \text{V} = 0.80 \, \text{V} - \frac{8.314 \frac{J}{mol \cdot K}(298 \, K)}{2(96485 \, C/mol)} \ln Q \nonumber\]
\[\ln Q = -16.35 \quad \Rightarrow \quad Q = 7.88 \times 10^{-8} \\
Q = \frac{[\ce{H+ }]^2}{[\ce{Ag+}]^2P_{\ce{H2}}}=\frac{[\ce{H+ }]^2}{(1.00)^2(1.00)}= 7.88 \times 10^{-8} \\
[\ce{H+}] = 2.81 \times 10^{-4} \, \text{M} \nonumber\]\[ \text{pH} = -\log (2.81 \times 10^{-4}) = 3.55 \nonumber\]
What is the minimum concentration of \(\ce{Ag+ }\) required for the reaction to be spontaneous in the forward direction when [\(\ce{Cu^2+ }\)]=1.00 M?
\[\ce{Cu(s) + 2Ag+ (aq) \rightleftharpoons Cu^2+ (aq) + 2Ag(s)} \nonumber\]
\[\begin{align*} \ce{Ag^+ (aq) + e^- &-> Ag(s)} \quad & E^\circ_{\text{red}} &= +0.80 \, \text{V} \\\\ \ce{Cu^{2+} (aq) + 2e^- &-> Cu(s)} \quad & E^\circ_{\text{red}} &= +0.34 \, \text{V} \end{align*}\]
- Answer
-
The reaction is spontaneous when \(E_{\text{cell}} > 0\).
Half-reactions:
- Anode (oxidation): \(\ce{Cu(s) -> Cu^{2+} (aq) + 2e^-}\) \(E^\circ_{\text{ox}} = -0.34 \, \text{V}\)
- Cathode (reduction): \(\ce{Ag^+ (aq) + e^- -> Ag(s)}\) \(E^\circ_{\text{red}} = +0.80 \, \text{V}\)
\[ E^\circ_{\text{cell}} = E^\circ_{\text{ox}} + E^\circ_{\text{red}} = (-0.34 \, \text{V}) + (+0.80 \, \text{V}) = +0.46 \, \text{V} \nonumber\]
Using the Nernst equation to find the minimum \([\ce{Ag^+}]\) for spontaneity. Set \(E_{\text{cell}} = 0\) to find the threshold for spontaneity:
\[ E_{cell} = E^\circ_{cell} - \frac{RT}{nF} \ln Q \nonumber\]
\[0 \, \text{V} = 0.46 \, \text{V} - \frac{8.314 \frac{J}{mol \cdot K}(298 \, K)}{2(96485 \, C/mol)} \ln Q \nonumber\]
\[\ln Q = 35.83 \quad \Rightarrow \quad Q = 3.6 \times 10^{15} \\
Q = \frac{[\ce{Cu^2+ }]}{[\ce{Ag+}]^2}=\frac{1.00}{[\ce{Ag+}]^2}= 3.6 \times 10^{15} \\
[\ce{Ag+}] = 1.7 \times 10^{-8} \, \text{M} \nonumber\]The minimum [\(\ce{Ag+}\)] required for the reaction to be spontaneous in the forward direction when [\(\ce{Cu^2+ }\)] = 1.00 M is
1.7 × 10−8 M.
Consider the galvanic cell at 25°C:
\[\text{Fe(s) | Fe}^{2+} \text{ (0.10 M) } || \text{Cd}^{2+} \text{ (1.00 M) | Cd(s)} \nonumber\]
Reduction half-reactions:
- \(\ce{Fe^{2+} (aq) + 2e^- -> Fe(s)} \quad E^\circ_{\text{red}} = -0.45 \, \text{V}\)
- \(\ce{Cd^{2+} (aq) + 2e^- -> Cd(s)} \quad E^\circ_{\text{red}} = -0.40 \, \text{V}\)
a) Calculate the standard cell potential, \(E^\circ_{\text{cell}}\).
b) Calculate the cell potential, \(E_{\text{cell}}\), under the given non-standard conditions.
c) Calculate the equilibrium constant \(K\) for the cell reaction.
d) Calculate the equilibrium concentrations of \(\ce{Fe^{2+}}\) and \(\ce{Cd^{2+}}\).
e) Determine the mass of cadmium deposited on the electrode, assuming a volume of 1.00 L, as the cell reaches equilibrium.
f) If a current of \(0.50 \, \text{A}\) is drawn from the cell, estimate how long it will take for equilibrium to be reached.
- Answer
-
a) From the cell notation, oxidation occurs at the left-hand electrode (\(\ce{Fe(s) ∣ Fe^2+ (aq) }\)) and reduction occurs at the right-hand electrode (\(\ce{Cd^2+ (aq) ∣ Cd(s)} \)). This means:
- Iron metal is oxidized to \(\ce{Fe^2+ }\)at the anode.
- Cadmium ions are reduced to cadmium metal at the cathode.
This also makes sense based on standard reduction potentials:
- \(\ce{Cd^2+ }\) has a higher (less negative) reduction potential than \(\ce{Fe^2+ }\), so cadmium ions are more easily reduced than iron ions.
Therefore, the overall reaction is:
Reaction: \(\ce{Fe(s) + Cd^{2+} (aq) \rightleftharpoons Fe^{2+} (aq) + Cd(s)}\)
\[ E^\circ_{\text{cell}} = E^\circ_{\text{ox}} + E^\circ_{\text{red}} = (+0.45 \, \text{V}) + (-0.40 \, \text{V}) = 0.05 \, \text{V} \nonumber \]
b) Cell potential under non-standard conditions:
Reaction: \(\ce{Fe(s) + Cd^{2+} (aq) \rightleftharpoons Fe^{2+} (aq) + Cd(s)}\)
\[ Q = \frac{[\ce{Fe^{2+}}]}{[\ce{Cd^{2+}}]} = \frac{0.10}{1.00} = 0.10 \nonumber\]
\[ E_{cell} = E^\circ_{cell} - \frac{RT}{nF} \ln Q = 0.05 \, \text{V} - \frac{8.314 \frac{J}{mol \cdot K}(298 \, K)}{2(96485 \, C/mol)} \ln (0.10) = 0.08 \, \text{V} \nonumber\]
c) Equilibrium constant \(K\):
At equilibrium, \(E_{\text{cell}} = 0\):
\[\begin{align*} \ln K &= \frac{nF}{RT} E^\circ_{\text{cell}}
\\ \ln K &= \frac{2(96485 \, C/mol)}{8.314 \frac{J}{mol \cdot K}(298 \, K)} (0.05 \, \text{J/C}) = 3.89 \\
K &= 49 \end{align*}\]d) Equilibrium concentrations:
Fe(s) +
Cd2+(aq) ⇌
Fe2+(aq)
+ Cd(s)
Initial
-
1.00 M
0.10 M
-
Change
-
-
+x
-
Equilibrium
-
1.00 - x
0.10 + x
-
\[ K = \frac{[\ce{Fe^{2+}}]}{[\ce{Cd^{2+}}]} = \frac{0.10 + x}{1.00 - x} = 49 \\
0.10 + x = 49 - 49 x \\ 50 x = 48.9 \\
x = 0.98 \, \text{M} \nonumber \][\(\ce{Cd^2+ }\)] = 0.02 M; [\(\ce{Fe^2+ }\)] = 1.08 M
e) For each moles of \(\ce{Cd^2+}\) that reacts, one mole of \(\ce{Cd(s)}\) is deposited on the electrode.
moles of \(\ce{Cd^2+}\) reacted: 0.98 mol/L (1.00 L) = 0.98 mol \(\ce{Cd^2+}\)
0.98 mol \(\ce{Cd}\) deposited \(\Rightarrow\) 0.98 mol (112.4 g/mol) = 110 g Cd
f) Equilibrium is reached when 0.98 mol of \(\ce{Cd^2+}\) reacts.
n = 2 mol electrons per mol \(\ce{Cd^2+}\).
Total charge required:
\[ Q = n F moles = 2 \times 96485 \, \text{C/mol} \times 0.98 \, \text{mol} = 189111 \, \text{C} \nonumber\]
We need to calculate time required with \(0.50 \, \text{A}\) current. Using \(I = Q/t\):
\[ t = \frac{Q}{I} = \frac{189111 \, \text{C}}{0.50 \, \text{C/s}} = 3.78 \times 10^5 \, \text{s} = 105 \, \text{hours} \nonumber\]
If a sample of iron and a sample of zinc come into contact, the zinc corrodes but the iron does not. If a sample of iron comes into contact with a sample of copper, the iron corrodes but the copper does not. Explain this phenomenon.
- Answer
-
When two different metals are in contact in the presence of an electrolyte (like water), they form a galvanic cell. The metal whose metal ion/metal half-reaction has the lower (more negative) standard reduction potential will oxidize (corrode) first, protecting the other metal, which acts as the cathode.
Relevant standard reduction potentials:
- Zinc (\(\ce{Zn^{2+}/Zn}\)): −0.76 V
- Iron (\(\ce{Fe^{2+}/Fe}\)): −0.45 V
- Copper (\(\ce{Cu^{2+}/Cu}\)): +0.34 V
Case 1: Iron and Zinc
Zinc oxidizes (corrodes) more easily than iron and acts as the anode, while iron is protected as the cathode.Case 2: Iron and Copper
Iron oxidizes (corrodes) more easily than copper and acts as the anode, while copper is protected as the cathode.This explains why zinc corrodes to protect iron (as in galvanized steel), while copper accelerates the corrosion of iron when in contact.
Consider the following electrolytic cell:
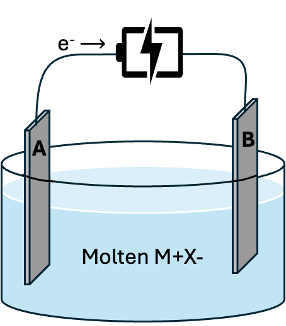
b) Write the half-reaction that occurs at the cathode.
- Answer
-
a) A is the anode where oxidation occurs (electrons are travelling away from A).
B is the cathode where reduction occurs (gaining electrons)
b) Cathode (reduction): \(\ce{M^+(l) + e^- \rightarrow M(l)}\)

