11.3: Cell Potentials
- Page ID
- 526880
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Use standard reduction potential tables to predict the direction of redox reactions, identify the anode and cathode in a galvanic cell, and calculate the standard cell potential (\( E_{cell}^{\circ} \)).
- Interpret the sign of \( E_{cell}^{\circ} \) in terms of spontaneity under standard conditions.
- Use standard reduction potential tables to compare the relative strength of oxidizing and reducing agents.
Cell Potentials
What drives a galvanic cell?
Consider the galvanic cell with the following overall reaction:
\[\ce{Zn (s) + Cu^{2+} (aq) \rightarrow Zn^{2+} (aq) + Cu(s)} \nonumber \]
In this cell, a current is produced when electrons flow externally from the \(\ce{Zn}\) anode to the \(\ce{Cu}\) cathode, where \(\ce{Cu^2+}\) is reduced. Why do electrons flow from zinc to copper in this cell?
We can think of the redox reaction as a competition for electrons. Since this reaction is spontaneous, \(\ce{Cu^2+}\) is better at gaining electrons than \(\ce{Zn^2+}\) and \(\ce{Zn}\) gives up electrons more readily than copper metal. The differing abilities of these metals to gain or lose electrons create a potential difference (cell potential) that pushes electrons through the external circuit. The more positive the cell potential, the greater the driving force for the redox reaction to occur spontaneously.
The cell potential (also called the electromotive force, EMF) measures the difference in electrical potential energy per unit charge between the two electrodes in a galvanic cell. Its units are volts (V), where 1 V = 1 J/C (joule per coulomb), indicating the amount of energy per unit of charge. A coulomb is a unit of electrical charge where one coulomb (C) is the charge of 6.242 x 1018 electrons. Just as water flows spontaneously downhill due to gravity, electrons flow “downhill” from higher to lower potential energy in a galvanic cell, allowing the cell to do electrical work.
A positive cell potential (Ecell > 0) indicates that the redox reaction is spontaneous, and electrons will flow through the external circuit from the anode to the cathode. A negative cell potential (Ecell < 0) indicates that the reaction is non-spontaneous under those conditions. When Ecell = 0, the system is at equilibrium, and no net reaction or electrical work occurs.
Different substances have different tendencies to lose or gain electrons, which affects the voltage measured in a galvanic cell.
For example, if we construct a galvanic cell similar to the \(\ce{Zn/Cu^2+}\) cell but replace copper with cobalt metal and 1 M \(\ce{Co^2+}\) in the cathode compartment, the measured voltage is not 1.10 V but only 0.51 V. This tells us that the difference in potential energy between the valence electrons of cobalt and zinc is smaller by 0.59 V than the difference between copper and zinc.
Standard Cell Potential
The measured cell potential also depends on the concentrations of the reacting species and the temperature of the system. To compare the abilities of different substances to gain or lose electrons, chemists need to measure cell potentials under comparable conditions. To do this, chemists define the standard cell potential (\( E_{cell}^{\circ} \)) as the potential of a cell measured under standard conditions:
- All solutions at 1 M concentration,
- All gases at 1 atm,
- Pure solids or liquids for other substances,
- At a fixed temperature, usually 25∘C.
By measuring cell potentials under these conditions, chemists can create a scale of relative potentials to predict both the direction of redox reactions and the magnitude of the driving force for those reactions.
Measuring Standard Cell Potentials
It is not possible to measure the potential of a single electrode in isolation. We can only measure the potential difference between two electrodes in a galvanic cell, similar to how we can only measure enthalpy changes or free energy changes, not their absolute values.
To establish a consistent reference point, chemists use the standard hydrogen electrode (SHE), which has a potential of exactly 0 volts under standard conditions. This allows the measurement of standard reduction potentials for other half-reactions relative to the SHE.
The standard hydrogen electrode (Figure \(\PageIndex{1}\)) consists of:
- A platinum electrode (inert and conductive),
- Immersed in a 1 M solution of \(\ce{H+}\),
- With \(\ce{H2(g)}\) bubbling over the electrode at 1 atm,
- At a temperature of 25 ∘C.
The half-reaction at the SHE is:
\[\ce{2H+ (aq) + 2e^{−} \rightarrow H2 (g)} \nonumber \]
The SHE can function as either the anode or cathode, depending on the other half-cell it is paired with in the galvanic cell, allowing measurement of the relative tendency of substances to gain or lose electrons.
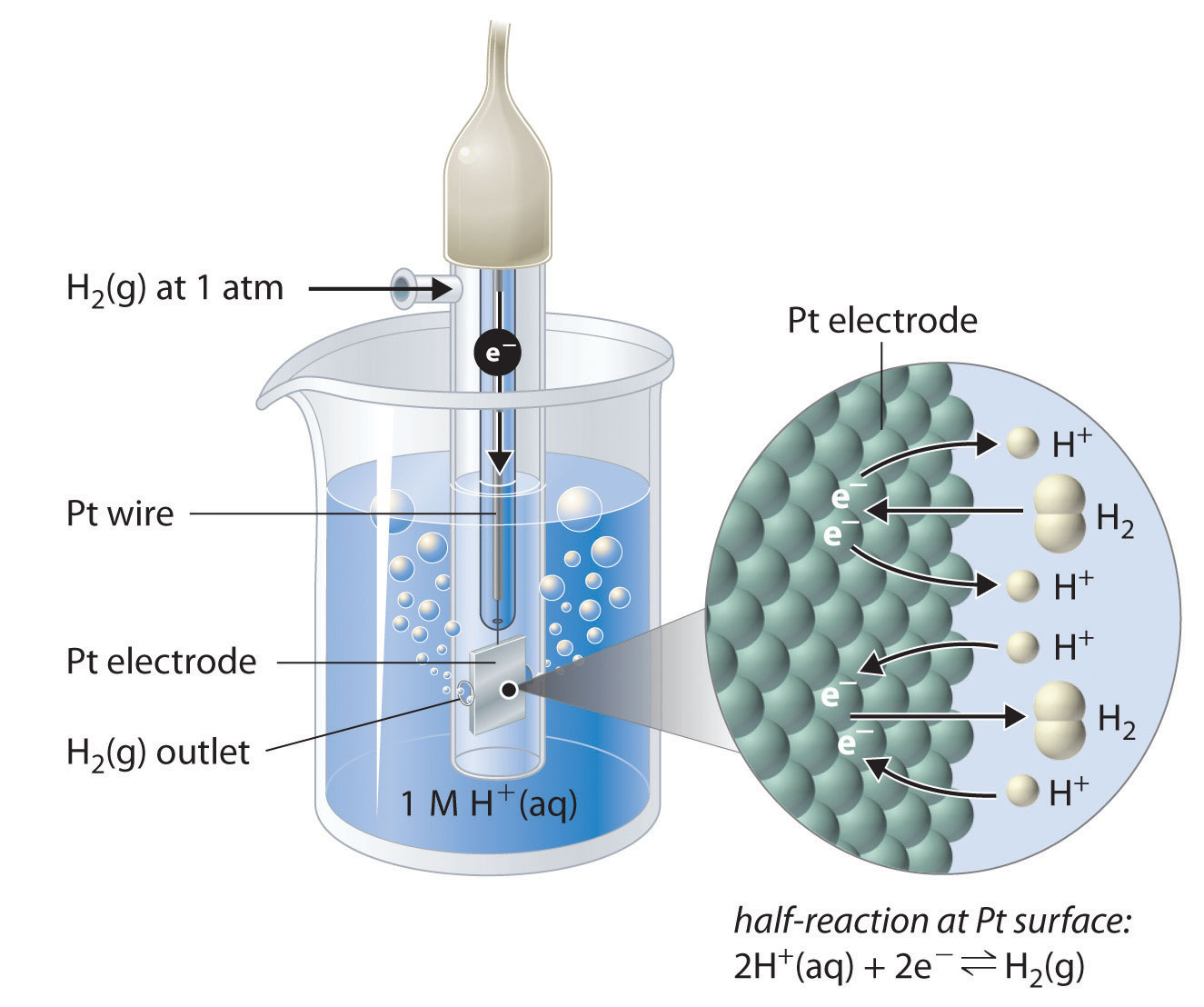
To measure the standard electrode potential of another half-reaction, we connect the electrode of interest to the SHE in a galvanic cell under standard conditions.
For example, to measure the standard reduction potential of zinc, we can construct the cell (Figure \(\PageIndex{2}\)):
\[\ce{Zn(s) | Zn^{2+} (aq,\, 1\, M) || H^{+}(aq,\, 1\, M) | H2(g,\, 1\, atm) | Pt(s)} \nonumber\]
In this setup:
- Zinc is oxidized at the anode: \(\ce{Zn(s) \rightarrow Zn^2+ (aq) + 2e^{-}}\)
- Hydrogen ions are reduced at the cathode: \(\ce{2H+ (aq) + 2e^{-} \rightarrow H2(g)}\)
- The voltmeter measures the cell potential of 0.76 V under standard conditions.

The standard cell potential can be calculated using:
\[E_{cell}^{\circ} = E_{red}^{\circ} + E_{ox}^{\circ} \nonumber \]
where:
- \(E_{red}^{\circ}\) is the standard reduction potential for the reduction half-reaction at the cathode
- \(E_{ox}^{\circ}\) is the standard oxidation potential for the oxidation half-reaction at the anode
In the zinc–SHE cell, we measure \(E_{cell}^{\circ}\) = 0.76 V.
We know that the SHE (cathode) reduction potential is \(E_{red}^{\circ}\)= 0.00 V. Zinc is oxidized at the anode, so:
\[\begin{align*} E_{cell}^{\circ} &= E_{red}^{\circ} + E_{ox}^{\circ} \\ 0.76\ \text{V} &= 0.00\ \text{V} + E_{ox}^{\circ} \\
E_{ox}^{\circ} &=0.76\ \text{V} \end{align*}\]
Because oxidation is the reverse of reduction, the standard reduction potential for the \(\ce{Zn^2+ /Zn}\) couple is the negative of its oxidation potential:
\[E_{red}^{\circ}=- E_{ox}^{\circ}= -0.76 V \nonumber\]
This process demonstrates how standard reduction potentials are experimentally determined using the SHE as a reference. Chemists have constructed tables of standard reduction potentials for many half-reactions. These values allow us to:
- Predict the direction of redox reactions, and
- Calculate the standard cell potential (\( E_{cell}^{\circ} \)) for many galvanic cells.
Interpreting Standard Reduction Potentials
The standard reduction potential of a half-reaction (\(E_{red}^{\circ}\)) measures how readily a species gains electrons under standard conditions, relative to SHE.
- A more positive \(E_{red}^{\circ}\) means the species is better at gaining electrons. It is more likely to be reduced, and thus acts as a stronger oxidizing agent.
- A more negative \(E_{red}^{\circ}\) means the species is less likely to gain electrons, and the reduced form of the species is a stronger reducing agent.
The standard oxidation potential (\(E_{ox}^{\circ}\)) for a half-reaction is the negative of the standard reduction potential for the reverse reaction:
\[E_{ox}^{\circ}=- E_{red}^{\circ} \nonumber\]
A species with a higher \(E_{ox}^{\circ}\) is a stronger reducing agent, because it more readily loses electrons.
For example, the standard reduction potential for the \(\ce{Cu^2+ /Cu}\) couple is +0.34 V, while for \(\ce{Zn^2+ / Zn}\) it is −0.76 V. Since +0.34 V > −0.76 V, \(\ce{Cu^2+ }\) is a stronger oxidizing agent than \(\ce{Zn^2+}\).
Understanding these values allows us to determine:
- Which half-reaction will occur at the cathode (the one with the more positive \(E_{red}^{\circ}\))
- Which will occur at the anode (the one with the less positive \(E_{red}^{\circ}\), written as an oxidation)
The values of standard reduction potentials also allow us to compare the relative strengths of oxidizing and reducing agents. The figure below summarizes these trends and helps visualize how standard reduction potentials guide predictions about electron flow and spontaneity in galvanic cells.
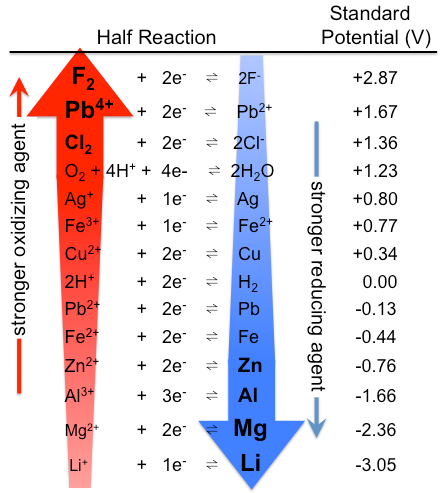
Compare \(\ce{Fe^{2+}}\) and \(\ce{Ag^{+}}\) as oxidizing agents, and \(\ce{Fe}\) and \(\ce{Ag}\) as reducing agents, using their standard reduction potentials.
Write the overall spontaneous reaction for a galvanic cell combining the \(\ce{Fe^{2+}/Fe}\) and \(\ce{Ag^{+}/Ag}\) half-cells under standard conditions, and calculate the standard cell potential, \(E_{cell}^{\circ}\).
Solution
From the standard reduction potential table:
\(\ce{Fe^{2+}(aq) + 2e^- \rightarrow Fe (s)} \quad E_{red}^{\circ} = -0.45 \, V\)
\(\ce{Ag^{+}(aq) + e^- \rightarrow Ag(s)} \quad E_{red}^{\circ} = +0.80 \, V\)
- Since \(\ce{Ag^{+}}\) has a higher \(E_{red}^{\circ}\) than \(\ce{Fe^{2+}}\), it is a stronger oxidizing agent.
When we reverse a half-reaction to write it as an oxidation, we change the sign of its \( E_{red}^{\circ} \) to get \(E_{ox}^{\circ}\). Looking at the oxidation half-reactions:
\(\ce{Fe (s) \rightarrow Fe^{2+}(aq) + 2e^- } \quad E_{ox}^{\circ} = 0.45 \, V\)
\(\ce{Ag(s) \rightarrow Ag^{+}(aq) + e^{-}} \quad E_{ox}^{\circ} = -0.80 \, V\)
- Since \(\ce{Fe}\) has a higher \(E_{ox}^{\circ}\) than \(\ce{Ag}\), it is a stronger reducing agent.
At the cathode (reduction): \(\ce{Ag^{+}(aq) + e^- \rightarrow Ag(s)}\)
At the anode (oxidation): \(\ce{Fe(s) \rightarrow Fe^{2+}(aq) + 2e^-}\)
To balance electrons, multiply the silver half-reaction by 2:
\(2 \times [\ce{Ag^{+}(aq) + e^- \rightarrow Ag(s)}]\)
Overall cell reaction:
\(\ce{Fe(s) + 2Ag^{+}(aq) \rightarrow Fe^{2+}(aq) + 2Ag(s)}\)
Calculating \(E_{cell}^{\circ}\):
\[ E_{cell}^{\circ} = E_{red}^{\circ} (\text{cathode}) + E_{ox}^{\circ} (\text{anode}) = 0.80 \, V + 0.45 \, V = 1.25 \, V \nonumber\]
Because \(E_{cell}^{\circ} > 0\), the reaction is spontaneous under standard conditions.
Compare \(\ce{Cu^{2+}}\) and \(\ce{Zn^{2+}}\) as oxidizing agents, and \(\ce{Cu}\) and \(\ce{Zn}\) as reducing agents, using standard reduction potentials. Write the overall reaction for a galvanic cell made with \(\ce{Cu^{2+}/Cu}\) and \(\ce{Zn^{2+}/Zn}\) half-cells under standard conditions and calculate the standard cell potential, \(E_{cell}^{\circ}\).
Given:
\(\ce{Cu^{2+}(aq) + 2e^- \rightarrow Cu(s)} \quad E_{red}^{\circ} = +0.34 \, V\)
\(\ce{Zn^{2+}(aq) + 2e^- \rightarrow Zn(s)} \quad E_{red}^{\circ} = -0.76 \, V\)
- Answer
-
\(\ce{Cu^{2+}}\) has a higher \(E_{red}^{\circ}\) than \(\ce{Zn^{2+}}\), so it is the stronger oxidizing agent.
\(\ce{Zn}\) has a higher \(E_{ox}^{\circ}\) (looking at the reverse reaction) than \(\ce{Cu}\), so it is the stronger reducing agent.
At the cathode (reduction):
\(\ce{Cu^{2+}(aq) + 2e^- \rightarrow Cu(s)} \quad E_{red}^{\circ} = +0.34 \, V\)
At the anode (oxidation):
\(\ce{Zn(s) \rightarrow Zn^{2+}(aq) + 2e^-} \quad E_{ox}^{\circ} = +0.76 \, V\)
Overall cell reaction:
\(\ce{Zn(s) + Cu^{2+}(aq) \rightarrow Zn^{2+}(aq) + Cu(s)}\)
Calculating the standard cell potential:
\[ E_{cell}^{\circ} = E_{red}^{\circ} (\text{cathode}) + E_{ox}^{\circ} (\text{anode}) = 0.34 \, V + 0.76 \, V = 1.10 \, V \nonumber\]
Since \(E_{cell}^{\circ} > 0\), the reaction is spontaneous under standard conditions.
Calculating Standard Cell Potentials
Once the anode and cathode are identified, the standard cell potential can be calculated:
\[E_{cell}^{\circ} = E_{red}^{\circ} + E_{ox}^{\circ} \nonumber \]
or equivalently:
\[E_{cell}^{\circ} = E_{red, cathode}^{\circ}-E_{red, anode}^{\circ} \nonumber\]
Both forms are valid; the first makes it explicit that one half-reaction is written as an oxidation, the other as a reduction.
Cell potential (voltage) is the potential energy per unit charge, so it is an intensive property. This means it does not depend on the amount of substance or the number of electrons transferred. As a result, \(E^{\circ}\) values are independent of the stoichiometric coefficients used in the half-reaction. The coefficients needed to balance the overall redox reaction do not affect the value of the cell potential, even though they determine the total charge and energy transferred during the reaction.
A positive standard cell potential (\(E_{cell}^{\circ}\) > 0) indicates that the redox reaction is spontaneous under standard conditions, and electrons will flow through the external circuit from the anode to the cathode. A negative cell potential (\(E_{cell}^{\circ}\) < 0) indicates that the redox reaction is non-spontaneous under those conditions.
Consider a galvanic cell that consists of Au3+/Au and Ni2+/Ni half-cells.
What is the standard cell potential for the galvanic cell?
What is the overall redox reaction that occurs in the cell?
Identify the oxidizing and reducing agents.
Solution
a) Using Table \(\PageIndex{1}\), the reactions involved in the galvanic cell, both written as reductions, are
\[\ce{Au^3+}(aq)+\ce{3e-}\rightarrow\ce{Au}(s) \hspace{20px} E^\circ_{red}=\mathrm{+1.50\: V} \nonumber \]
\[\ce{Ni^2+}(aq)+\ce{2e-}\rightarrow\ce{Ni}(s) \hspace{20px} E^\circ_{red}=\mathrm{−0.26\: V} \nonumber \]
Galvanic cells have positive cell potentials for spontaneous reactions. The half-reaction with the more positive standard reduction potential occurs at the cathode, while the one with the more negative potential occurs at the anode (as an oxidation).
Reverse the anode half-reaction and switch the sign of \(E_{red}^{\circ}\) to find \(E_{ox}^{\circ}\):
\[\begin{align*}
&\textrm{Anode (oxidation): }\ce{Ni}(s)\rightarrow\ce{Ni^2+}(aq)+\ce{2e-} \hspace{20px} E^\circ_\ce{ox}=-E^\circ_{\ce{red}}=\mathrm{+0.26\: V}\\
&\textrm{Cathode (reduction): }\ce{Au^3+}(aq)+\ce{3e-}\rightarrow\ce{Au}(s) \hspace{20px} E^\circ_{red}=\mathrm{+1.50\: V}
\end{align*} \nonumber \]
To balance the electrons, multiply the oxidation half-reaction by 3 and the reduction half-reaction by 2:
\[\begin{align*}
&\textrm{Anode (oxidation): }3\ce{Ni}(s)\rightarrow3\ce{Ni^2+}(aq)+\ce{6e-} \hspace{20px} &E^\circ_\ce{ox}=-E^\circ_{\ce{red}}=\mathrm{+0.26\: V}\\
&\textrm{Cathode (reduction): }2\ce{Au^3+}(aq)+\ce{6e-}\rightarrow3\ce{Au}(s) \hspace{20px} &E^\circ_{red}=\mathrm{+1.50\: V} \\
&\overline{ \textrm{Overall reaction: } \ce{3Ni}(s)+\ce{2Au^3+}(aq)\rightarrow\ce{3Ni^2+}(aq)+\ce{2Au}(s)} &\overline{\hspace{20px} E^\circ_{cell}=\mathrm{+1.76\: V}}
\end{align*} \nonumber \]
The reduction potentials are not scaled by the stoichiometric coefficients when calculating the standard cell potential:
\[E_{cell}^{\circ} = E_{red}^{\circ} + E_{ox}^{\circ}=\mathrm{1.50\: V + 0.26\: V=1.76\: V} \nonumber \]
From the half-reactions, nickel (Ni) is oxidized, so it is the reducing agent. Gold (III) ions (\(\ce{Au^3+}\)) are reduced, so they are the oxidizing agent.
A galvanic cell consists of an Mg electrode in 1 M Mg(NO3)2 solution and an Ag electrode in 1 M AgNO3 solution. Calculate the standard cell potential at 25 °C.
- Answer
-
\[\ce{Mg^2+}(aq)+\ce{2e-}\rightarrow\ce{Mg}(s) \hspace{20px} E^\circ_{red}=\mathrm{−2.37\: V} \nonumber \]
\[\ce{Ag+}(aq)+\ce{e-}\rightarrow\ce{Ag}(s) \hspace{20px} E^\circ_{red}=\mathrm{+0.80\: V} \nonumber \]
Since the cell is galvanic, the element with the more negative reduction potential will undergo oxidation at the anode. We reverse the anode half-reaction and switch the sign of \(E_{red}^{\circ}\) to find \(E_{ox}^{\circ}\):
\[\begin{align*}
&\textrm{Anode (oxidation): }\ce{Mg}(s)\rightarrow\ce{Mg^2+}(aq)+\ce{2e-} \hspace{20px} &E^\circ_\ce{ox}=-E^\circ_{\ce{red}}=\mathrm{+2.37\: V}\\
&\textrm{Cathode (reduction): }2\ce{Ag^+}(aq)+\ce{2e-}\rightarrow2\ce{Ag}(s) \hspace{20px} &E^\circ_{red}=\mathrm{+0.80\: V} \\
&\overline{ \textrm{Overall reaction: } \ce{Mg}(s)+\ce{2Ag^+}(aq)\rightarrow\ce{Mg^2+}(aq)+\ce{2Ag}(s)} &\overline{\hspace{20px} E^\circ_{cell}=\mathrm{+3.17\: V}}
\end{align*} \nonumber \]The standard cell potential is:
\[E_{cell}^{\circ} = E_{red}^{\circ} + E_{ox}^{\circ}=\mathrm{0.80\: V + 2.37\: V=3.17\: V} \nonumber \]
Example \(\PageIndex{3}\)
A galvanic cell with a measured standard cell potential of 0.27 V at 25 °C is constructed using two beakers connected by a salt bridge. One beaker contains a strip of gallium metal in 1 M \(\ce{GaCl3}\), and the other contains a piece of nickel in 1 M \(\ce{NiCl2}\). When connected:
- Gallium oxidizes at the anode:
\[\ce{Ga(s) \rightarrow Ga^{3+}(aq) + 3e^{-}} \nonumber\] - Nickel ions are reduced at the cathode:
\[\ce{Ni^{2+}(aq) + 2e^{-} \rightarrow Ni(s)} \nonumber\]
If the oxidation potential for gallium under standard conditions is +0.55 V, calculate the standard reduction potential for \(\ce{Ni^{2+}/Ni}\) under standard conditions.
Solution:
Given:
- \(E_{cell}^{\circ} = 0.27 \, \mathrm{V}\)
- \(E_{ox}^{\circ} = +0.55 \, \mathrm{V}\)
We use the relationship:
\[ E_{cell}^{\circ} = E_{red}^{\circ} + E_{ox}^{\circ} \nonumber\]
Solving for the unknown reduction potential:
\[ E_{red}^{\circ} = E_{cell}^{\circ} - E_{ox}^{\circ} = 0.27 \, \mathrm{V} - 0.55 \, \mathrm{V} = -0.28 \, \mathrm{V} \nonumber\]
Thus, the standard reduction potential for \(\ce{Ni^{2+}/Ni}\) is:
\[ E_{red}^{\circ} = -0.28 \, \mathrm{V} \nonumber\]
Exercise \(\PageIndex{3}\)
A galvanic cell is constructed with one compartment that contains a mercury electrode immersed in a 1 M aqueous solution of mercuric acetate \(\ce{Hg(CH3CO2)2}\) and one compartment that contains a strip of magnesium immersed in a 1 M aqueous solution of \(\ce{MgCl2}\). When the compartments are connected, a potential of 3.22 V is measured and the following half-reactions occur:
- cathode: \[\ce{Hg^{2+}(aq) + 2e^{−} \rightarrow Hg(l)} \nonumber\]
- anode: \[\ce{Mg(s) \rightarrow Mg^{2+}(aq) + 2e^{−}} \nonumber\]
If the potential for the oxidation of \(\ce{Mg}\) to \(\ce{Mg^{2+}}\) under standard conditions is 2.37 V, what is the standard reduction potential for the reaction that occurs at the cathode?
- Answer
-
\[\begin{align*} E_{cell}^{\circ} &= E_{red}^{\circ} + E_{ox}^{\circ} \\3.22 \, \mathrm{V} &= E_{red}^{\circ} + 2.37 \, \mathrm{V} \\E_{red}^{\circ} &= 0.85 \, \mathrm{V}\end{align*} \]
Summary
The cell potential (\(E_{cell}\)) is a measure of the driving force for the reaction. The voltage (cell potential) in a galvanic cell depends on the identity of the reacting substances, their concentrations, and the temperature. The cell potential under standard conditions (1 M for solutions, 1 atm for gases, pure solids or liquids for other substances) is called the standard cell potential (\(E_{cell}^{\circ}\)).
Because we can only measure potential differences between electrodes, chemists use the Standard Hydrogen Electrode (SHE) as a reference, assigning it a potential of 0 V. This allows the determination of standard reduction potentials (\(E_{red}^{\circ}\)) for many half-reactions.
The standard oxidation potential of a half-reaction is equal in magnitude and opposite in sign to its reduction potential. Importantly, because voltage is an intensive property, standard cell potentials do not depend on the stoichiometric coefficients used to balance the overall redox reaction.
The standard cell potential for a galvanic cell can be calculated using:
\[E_{cell}^{\circ} = E_{red}^{\circ} + E_{ox}^{\circ} \nonumber \]
A positive standard cell potential (\(E_{cell}^{\circ}\) > 0) indicates that the redox reaction is spontaneous under standard conditions, with electrons flowing through the external circuit from the anode to the cathode.
Standard reduction potentials can also be used to compare the relative strengths of oxidizing and reducing agents and to predict which redox reactions will be spontaneous under standard conditions.

