3.E: Solids, Liquids, and Phase Transitions (Exercises)
- Page ID
- 69604
These are homework exercises to accompany the Textmap created for "Principles of Modern Chemistry" by Oxtoby et al. Complementary General Chemistry question banks can be found for other Textmaps and can be accessed here.
Q.1
If a substance has relatively strong intermolecular forces, a high melting point, and is not easily compressed, will this substance be a solid, liquid, or gas?
- Solution
-
The substance is a solid because solids have relatively stronger intermolecular forces than liquids or gases. These strong intermolecular forces strongly hold the molecules in the solid together which makes it hard to compress a solid. Solids also have higher melting points because you need to put a lot more energy into solids to break apart the intermolecular forces to make the solid change phases.
Q.3
An unknown sample at \(25^oC\) had a volume of \(3.00\times 10^{14} \mu m^3\) and a mass of \(3.20\times 10^3\ g\).
- Is this sample most likely in a gaseous state or a condensed one? Why? (HINT: The density of water is \(1.000\frac{g}{mL})\).
- After completing mass spectroscopy the molar mass of the material was found to be 127 g mol-1, what is the molar volume at \(25^oC\) from using the answer in part (a).
- Solution
-
We need to compute the density of the liquid first:
\[\left(\dfrac{3.2 \times 10^3 g\;}{3.0 \times 10^{14} \cancel{µm^{3}}} \right)\left(\dfrac{1.0 \times 10^{12}\cancel{µm^{3}}\;}{\textrm{1} \textrm{ cm}^{3}\;}\right )=1.07 \times 10^{1}\textrm{g cm}^{-3}\nonumber \]
This material is known to be condensed because its density is higher than that of water.
Calculate the molar volume by:
\[\left(\dfrac{\textrm{1} \textrm{ cm}^{3}\;}{\textrm{10.7} \cancel{g}\;}\right)\left(\dfrac{127\cancel{g}\;}{\textrm{1} \textrm{ mol}\;}\right )=1.19\times10^{1}\textrm{cm}^{3} {mol}^{-1}\nonumber \]
Q.6A
If the volume of a substance changes from 300 \(cm^3\) to \(313\ cm^3\) when it is heated from \(25^oC\) to \(40^oC\), is the substance ideal gas, nearly ideal gas, or condensed?
- Solution
-
Temperature change = \(15^oC\)
\[\text{Volume change ratio:} \dfrac{(313-300)}{300} = \dfrac{13}{300} \nonumber\]
Hence, change percentage per \(^oC\) is
\[\dfrac{13}{300} \times \dfrac{1}{15} \times 100\%= \dfrac{13}{1500} \% = 0.288\%\nonumber\]
Since \(0.288\%\) is close to the ideal gas percentage of \(0.366\%\), it is a nearly ideal gas.
Q.6B
Cooling a sample of matter from 130° to 50° at a constant pressure causes its volume to increase from 769.1 to 930.1 cm3. Classify the material as nearly ideal gas, a non ideal gas, or condensed.
- Solution
-
Charles' Law - Ideal Gases
\[\dfrac{V_{1}}{T_{1}}=\dfrac{V_{2}}{T_{2}}\nonumber \]
\[0.00191 \dfrac{L}{K} = 0.00288 \dfrac{L}{K}\nonumber \]
The material is a non-ideal gas.
Q.7
The molar volume of a substance is the volume occupied by one mole of the substance. The molar volume of a typical solid or liquid is \(10\frac{cm^3}{mol}\) to \(100\frac{cm^3}{mol}\), while the molar volume of a gas under the same conditions is about \(24,000\frac{cm^3}{mol}\). What does the similarity of the molar volumes of solid and liquid forms of the same substance suggest? What does the great difference of the the molar volumes of solid/liquid and gas forms of the same substance suggest?
- Solution
-
The similarity of the molar volumes of solid and liquid forms of the same substance suggests that the distance between neighboring molecules of the substance in solid phase is approximately the same as the distance between neighboring molecules in liquid phase. The great difference of the molar volumes of solid/liquid and gas forms of the same substance suggests that the distance between neighboring molecules of the substance in gas phase is greater the distance between neighboring molecules in solid/liquid phase. This would explain why solids and liquids are called condensed states of matter, because the particles in these two phases are very close together, hence, solids and liquids have definite volumes. While the particles in the gas phase are so far away from each other that they can move freely at high speed, allowing the gas substance to assume the shape and volume of its container.
Q.9
Suppose you have to choose between solid \(\ce{I_2}\) and solid \(\ce{NH_4Cl}\) to fill your cushion and you prefer softer cushions, which one would you choose and why?
- Solution
-
Non-directional ion-ion interaction is the dominant intermolecular interaction solid \(\ce{NH_4Cl}\) has, and weaker London dispersion forces are the main intermolecular interaction \(\ce{I_2}\) has, while the feeling of softness (indentation that breaks bonds in the solid) of the two solids depends on their strength of intermolecular interactions; in this case \(\ce{I_2}\) has weaker intermolecular interactions and will feel softer.
Q.11
The diffusion constant is defined as the amount of substance that when diffusing from a region of high concentration to that of a low concentration goes through each unit of cross section per unit time. What happens to the diffusion constant, at constant temperature, as density of a liquid decreases, as the density of a solid increases, and as the density of a gas decreases? Explain the phenomena.
- Solution
-
As the density of a liquid decreases, the diffusion constant will increase. This is because as density of the liquid decreases, there is more space in between the liquid molecules, and hence more movement is possible for the liquid molecules.
As density of a solid increases, diffusion constant will decrease. Similarly, in concept for the liquid molecules, if the density of a solid increases, there is even less space between the solid molecules than there was before. This further restricts the movements of the solid molecules and decreases diffusion. Note: solids also undergo diffusion; however, it occurs at an extremely slow rate.
As the density of gas decreases, diffusion constant will increase. As the density of a gas decreases, collision between gas molecules will occur less frequently, thus increasing freedom of movement for gas molecules and increasing the diffusion constant.
Q.15
For the following chemicals list attractive intermolecular forces that you expect to see with each chemical. Of the forces you listed for each example, rank the intermolecular forces from strongest to weakest.
- \(\ce{He}\)
- \(\ce{H_2O}\)
- \(\ce{NaCl}\)
- \(\ce{CH_4}\)
- \(\ce{CO}\)
- \(\ce{O_2}\)
- Solution
-
- London dispersion forces
- Hydrogen bonding > dispersion forces
- Ionic bonding > dispersion forces
- London dispersion forces
- Dipole-dipole forces > dispersion forces
- London dispersion forces
Q.17
Which of the the following will be most strongly attracted to a lithium ion:
- fluoride ion
- a molecule of hydrogen fluoride
- atom of Argon
- Solution
-
A fluoride ion will be most strongly attracted to a lithium ion. The attraction between unlike charges such as lithium and fluoride are much stronger than the ion dipole attraction between \(\ce{Li^+}\) and \(\ce{HF}\) and the ion-induced dipole attraction between \(\ce{Li^+}\) and \(\ce{Ar}\).
Q.19
Estimate the bond length of \(\ce{He2}\), \(\ce{Ar2}\), and \(\ce{Xe2}\) from the potential energy curves below. For each interacting pair, identify the attractive and repulsive distances. What are the intermolecular forces exist in each of the pair of molecules? Order the potential interactions in term of strength of intermolecular forces.
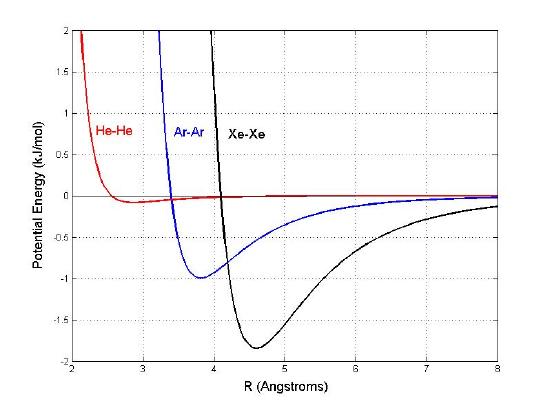
- Solution
-
- \(\ce{He2} \approx 2.7Å\)
- \(\ce{Ar2} \approx 3.8Å\)
- \(\ce{Xe2} \approx 4.5Å\)
Repulsion is when R less than R at equilibrium. Attraction is when R is bigger than R at equilibrium.
Increasing order of intermolecular forces: \(\ce{He2}\) < \(\ce{Ar2}\) < \(\ce{Xe2}\). The intermolecular force that the molecules have is London Dispersion Force (Van der Waals force). Larger molecules tend to have greater polarizability because they have more electrons and their electrons are further away from the nucleus. Therefore, LDF tend to get stronger when the molecule becomes larger. Based on the graph, the higher the potential energy, the stronger the interaction is.
Q.23
Arrange the following substances in order of decreasing normal boiling points and explain the rationale.
- \(\ce{CH_3CH_2CH_2CH_2CH_3}\)
- \(\ce{CH_3CH_2CH_2CH_2OH}\)
- \(\ce{CH_4}\)
- \(\ce{CH_3CH(CH_3)CH_2CH_3}\)
- Solution
-
\[\ce{CH_3CH_2CH_2CH_2OH > CH_3CH_2CH_2CH_2CH_3 > CH_3CH(CH_3)CH_2CH_3 > CH_4 }\nonumber \]
1-Butanol has the greatest boiling point due to strong hydrogen bonding with the alcohol group. Pentane has the second strongest boiling point due to its systematical structure and large London Dispersion force. Although 2-methylbutane has the same molecular mass as pentane, its geometrical structure hinders stacking which leads to lower intermolecular force. Therefore, 2-methylbutane has the lowest boiling point.
Q.24
You are given four beakers A, B, C, and D with four different chemicals. You forgot to label the beakers, so to identify them you boiled them to find their normal boiling points. The order of the boiling points came out to be B>D>A>C. If the chemicals in the beakers were \(\ce{HF}\) (Hydrogen Fluoride), \(\ce{Ar}\) (Argon), Cesium Chloride \(\ce{CsCl}\) and Hydrochloric Acid \(\ce{HCl}\), assign the chemicals to their respective beakers and give the reasoning behind your answer.
- Solution
-
The primary intermolecular forces in the compounds are
- \(\ce{HF}\) → Hydrogen Bonding
- \(\ce{Ar}\) → Dispersion Forces
- \(\ce{CsCl}\) → Ionic Bonding
- \(\ce{HCl}\) → Dipole-Dipole Interactions
Ionic Bonding > Hydrogen Bonding > Dipole-Dipole Interactions > Dispersion Forces
The stronger the intermolecular forces, the lower the vapor pressure, hence the boiling point would be higher.
Hence the beakers contain
- A = \(\ce{HCl}\)
- B = \(\ce{CsCl}\)
- C = \(\ce{Ar}\)
- D = \(\ce{HF}\)
Q.25
Like a normal human being, Kris enjoys breathing. But unfortunately for Kris, she is clinically paranoid, and feels as though she's breathing in a little too much ethanol. To calm Kris down, you say that as a vapor, ethanol exists, to an extent, as a dimer, (\(\ce{(CH3CH2OH)2}\)), in which two \(\ce{CH3CH2OH}\) molecules are held together by hydrogen bonds. Propose and draw a reasonable structure for this dimer to help Kris deal with her problems.
- Solution
-
Hydrogen bonds are a type of intermolecular forces. It is the bond between a hydrogen atom and a high electronegative atom such as N, O, and F. The only hydrogen bonding which can take place between the ethanol molecules is between one's oxygen and the other's hydrogen bonded onto the other's oxygen. So any two membered structure of two ethanol molecukes with this criteria indicated is acceptable.
Q.25
Acetic acid (\(\ce{CH3COOH}\)) forms a dimer in the gas phase, where two acetic acid molecules are held together by hydrogen bonds. Draw a reasonable structure for this dimer.
- Solution
-

The diagram above shows a reasonable structure of a acetic acid dimer, where the dash lines represent hydrogen bonds.
Q.26
Hypochlorous acid (\(\ce{HOCl}\)) is a similar compound to \(\ce{HOF}\), which is the simplest possible compound that allows comparison between fluoride and oxygen in their abilities to form hydrogen bonds. Although \(\ce{Cl}\) attracts electrons more strongly than \(\ce{O}\), solid \(\ce{HOCl}\) cannot form \(\ce{H-Cl}\) bonds. Draw the proposed structure for chains of \(\ce{HOCl}\) molecules in the crystalline state. The bond angle for \(\ce{HOCl}\) is \(103^o\).
- Solution
-

Q.27
How do the boiling points of hydrogen halides differ from that of hydrogen fluoride (\(\ce{HF}\)). Explain your reasoning. Answer: \(\ce{HF}\) has a much higher boiling point (\(20^oC\)) compared to the other hydrogen halides. This is because \(\ce{HF}\) is capable of forming hydrogen bonding within its compounds.
- Solution
-
Fluorine is capable of doing hydrogen bonding as opposed to the other halogens in the periodic table. Since fluorine is the element with the highest electronegativity, the hydrogen-fluorine bond in hydrogen fluoride is highly polarized, creating a partial positive charge (δ+) on the hydrogen and, a negative charge (δ-) on the fluorine atom. Furthermore, the lone pairs situated on the fluorine atom are in the second energy level, thus they are very close and the negative charge on the atom is very concentrated, thus it has a strong attraction force. Hydrogen bonds form between the positively charged H atoms and the lone pair of the F atom. The other halogens are not capable of hydrogen bonding because they are not as electronegative as fluorine and they are larger in size. Thus the bond within the molecule is not as polarized and the lone pairs on the halogen atom are not as concentrated. Thus, the stronger the intermolecular forcers of the liquid, the harder it is for a molecule to gain enough energy to overcome the intermolecular forces that bond it in a liquid. The more energy is required to enter the gas phase. The higher the boiling point. Fluorine has higher intermolecular forces, thus it has a higher boiling point compared to the other hydrogen halides.
Q.31
Oxygen is stored at a temperature of 105 K and a pressure of 3.356 atm. If the volume of the container is 2.5 L, calculate the number of moles of oxygen in the container. Compare this number of moles to the number of moles in the same container at standard pressure and 298 K. Is it fewer, more, or unchanged?
- Solution
-
This is an ideal gas law problem, so the formula \(PV=nRT\) should be used.
\(P=3.356 \, \text{atm}\) \(V=2.5 \, \text{L}\) \(n=?\) \(R=0.0821 \dfrac{\text{L} \ \text{atm}}{\text{mol} \ \text{K}}\) \(T=105 K\)
\[n= \dfrac{3.356 \times 2.5}{0.0821 \times 105} \, \text{mol} \nonumber \]
\[n= 0.9733 \, \text{mol} \nonumber \]
Standard pressure = 1 atm
\[n=\dfrac{1\times 2.5}{0.0821\times 298}\nonumber \]
\[n= 0.102 \, \text{mol} < 0.9733 \, \text{mol} \nonumber \]
Therefore, under standard conditions, there are fewer moles of oxygen in the container.
Q.35
Consider the reaction at 25ºC.
\[\ce{CaC2(s) + 2H2O(l) -> C2H2(g) + Ca(OH)2(s)} \nonumber \]
If the total pressure is 0.9124 atm and the vapor pressure of water at this temperature is 0.0313 atm. What is the mass of acetylene (\(\ce{C2H2}\)) per liter of "wet" acetylene collected by this reaction (i.e., collected over a pool of water)? Assume all gases behave ideally.
- Solution
-
Partial pressures in gases are additive via Dalton's Law.
- \(P_T= 0.9124 atm\)
- \(P_{\ce{H2O}}= 0.0313 atm\)
\[P_T-P_{\ce{H2O}}=P_{\ce{C2H2}} = 0.8811 atm \nonumber\]
Using the Ideal Gas Law, moles per liter of acetylene can be found by rearranging the equation:
\[\ce\dfrac{n}{V}=\dfrac{P_{\ce{C2H2}}}{RT}\nonumber \]
\[\dfrac {0.8811}{0.082057 \times 298.15} =\dfrac{0.036 mol}{1 L}\nonumber \]
The question asks for grams per liter, so:
\[\left (\dfrac{0.036 \: \cancel{mol \; C_2H_2}}{1 L} \right ) \left (\dfrac{26.036\; g C_2H_2}{1\: \cancel{mol\; C_2H_2}} \right ) = 0.9376\; \dfrac{g}{L}\nonumber \]
Q.39
The highest value of sea-level pressure on Earth occurs in Siberia where the Siberian High often allows water to boil at 80oC. Using chart 10.16 on page 431 of the text book, what can the fraction of pressure be in this location?
- Solution
-
According to the graph, a location where the boiling temperature is 80oC correlates approximately to a fraction of 0.5 atm pressure.
Q.41
Water (\(\ce{H2O}\)) has a melting point of \(0.00\text{°C}\) and a boiling point of \(100.0\text{°C}\). Benzene (\(\ce{C6H6}\)) has a melting point of \(5.5\text{°C}\) and a boiling point of \(80.1\text{°C}\). At \(20.0\text{°C}\), which of the two substances would be expected to have a greater surface tension? Explain?
- Solution
-
At \(20.0\text{°C}\), water \(\ce{H2O}\) has a greater surface tension (\(72.86\dfrac{mN}{m}\)) than benzene, (\(\ce{C6H6}\)), (\(28.88\dfrac{mN}{m}\)) because the intermolecular forces between water molecules are stronger than the intermolecular forces between benzene molecules. Water is capable of forming hydrogen-bonds, whereas the only forces that act in benzene are London dispersion forces.
Surface tension is the energy/work required to increase the surface area of a liquid. Molecules at the surface of a liquid do not experience any intermolecular interactions on one interface with air and therefore experience a net attractive force towards the center of the liquid. For surface molecules, the stronger the intermolecular forces between the molecules of the liquid, the stronger the net attractive force towards the center of the liquid will be. Compared to benzene, water possesses stronger intermolecular forces, therefore its surface molecules exhibit a stronger net attractive force towards the center of the liquid. As a result, more energy/work is required to counteract the net attractive force in order to increase the surface area. This indicates that for any liquid, stronger intermolecular forces allow for stronger surface tensions.
Q.43
At gallium’s melting point of \(302.91K\), its density is \(6.095\frac{g}{cm^3}\). The density of solid gallium under standard conditions is \(5.91\frac{g}{cm^3}\). When \(Ga\) is at \(301.91K\) and pressure is strongly increased, will \(Ga\) undergo a phase change?
- Solution
-
Compression favors the denser phase. Since \(Ga\) is a solid at \(301.9K\), then it will undergo a phase change to become a liquid.
Q.45
Given the information below, sketch the phase diagram of Nitrogen:
- Triple point: 0.1252 bar, -210°C
- Normal boiling point: 1 bar, -195.8°C
- Normal melting point: 1 bar, -210°C
- Solution
-
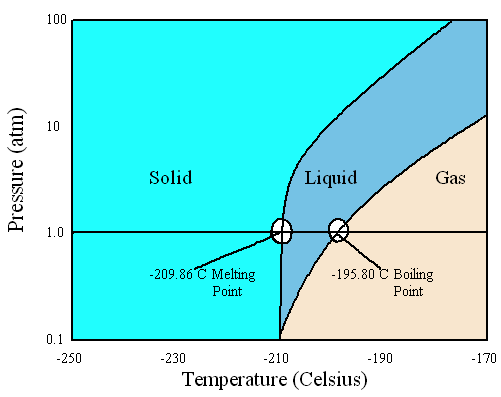
Normally, phase diagrams show pressures below that of the critical point.
Q.47
Use the phase diagram of water to determine whether water is a solid, a liquid, or a gas at each of the following combinations of temperature and pressure.
- \(1\ atm\) and \(20^oC\)
- \(0.006\ atm\) and \(100^oC\)
- \(210\ atm\) and \(100^oC\)
- \(10\ atm\) and \(50^oC\)
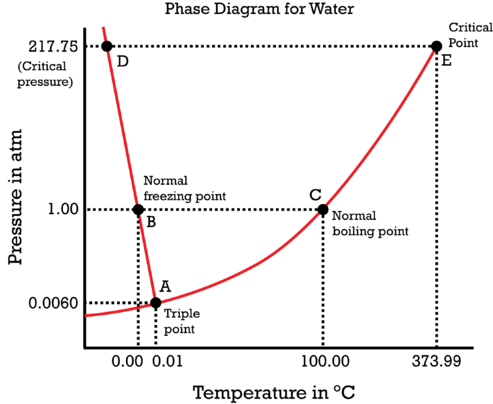
Figure used with permission (CK-12 Foundation – Christopher Auyeung)
- Solution
-
Using the phase diagram of water,
- Liquid
- Gaseous
- Liquid
- Liquid
Q.53
What phase does candle wax exist in? How about butter?
- Solution
-
Matter can exist in different phases depending on the temperature of the substance. For example, candle wax and butter can exist as a solid at room temperature, but when enough heat is applied to these substances, they can exist in a liquid or a gaseous phase.
Q.59
The equilibrium vapor pressure of water at \(19^oC\) is \(0.02168\,atm\). A humidifier is placed in a room with a volume of \(180m^3\) and operates until the the room becomes saturated with water vapor. Initially there is no water vapor in water vapor in the air. Assuming that the room is closed completely from the outside such that water vapor cannot escape, calculate the mass of water that has passed into the air.
- Solution
-
The air in the room becomes saturated once the vapor pressure of water in the room is equivalent to the equilibrium vapor pressure of water. Plug in given values into the ideal gas law to find the number of moles of water in the room when it is saturated, and then convert to grams.
\[PV=nRT\nonumber \]
\[(0.02168atm)(180m^{3})(\dfrac{1000L}{m^{3}})=(n)(0.08206\frac{L\ atm}{mol\ K})(292.15K)\nonumber \]
\[n=162.77mols\nonumber \]
\[m=162.77mols\times \dfrac{18.02g}{mol}=2930g\nonumber \]
Q.65
A cooling bath is a mixture that is primarily liquid which is kept at a constant, low temperature. While in the lab, Po’lah accidently severed its hand after trying to make some mac and cheese. As a result it had to immediately transfer its hand to a cooling bath to sufficiently preserve it but not so that it could be of some use later on. In order to achieve this, the cooling bath had to be kept at around \(0^{\circ}C\). The only liquids it had access to were water and methanol, both at room temperature, and the only cooling agents that it had were liquid nitrogen and dry ice (solid carbon dioxide). What combination did Po’lah use and why?
Relevant Information:
- Carbon Dioxide: sublimes at \(-78.5^{\circ}C\)
- Nitrogen: boils at \(-195.8^{\circ}C\)
- Water: freezes at \(0^{\circ}C\)
- Ethanol: freezes at \(-143.7^{\circ}C\)
- Solution
-
This question is a bit tricky. The coolants Liquid Nitrogen and Dry ice, (\(\ce{CO2 (s)}\)), both turn into gasses at very low temperatures. After they turn into gaseous, they are no longer “useful”, since they cannot be added into the bath. Therefore, after adding sufficient amounts of either of the coolants to either of the liquids, the temperature of the bath would decrease way past the freezing point of either liquid, resulting in a cooling “block” rather than a bath. So what is the deal? Is this problem unsolvable?
Fortunately, it isn’t. Think about a glass of ice water. If enough ice is put into the water, then eventually the water and ice would equilibrate at \(0^{\circ}C\) which is the equilibrium point of the water where both its solid and liquid states can exit. Unfortunately, while the ice is not available at this time, the same concept can be applied. Remember, if enough of either coolant is used, then the entire cup of water will freeze over. However, if just enough of either coolant is put in so that the cooling bath remains at \(0^{\circ}C\), a cooling bath that is somewhat solid and somewhat liquid will form, giving an adequate place for Po’lah to put its hand. Water is perfect for this because it remains a liquid at \(0^{\circ}C\), and cannot exist as such at any lower temperature. Since Ethanol freezes at \(-143.7^{\circ}C\), adding dry ice or liquid nitrogen would bring the cooling bath much lower than \(0^{\circ}C\), which would destroy Po’lah’s hand
Thus, it doesn’t matter what cooling agent is used, either can bring water down to \(0^{\circ}C\). However, methane cannot be used.
Abstract: Add a little of either coolant to bring the water down to \(0^{\circ}C\), and it will remain at both a liquid and a solid which creates a \(0^{\circ}C\) cooling bath. Methanol cannot be used.
Q.71
The melting points of the chlorides of third period elements are: \(\ce{NaCl} = 1074 \,K\), \(\ce{MgCl_2} = 987\,K\), \(\ce{AlCl_3} =465\,K\), \(\ce{SiCl_4} = 204.4\, K\), \(\ce{PCl_3} = 179\, K\). Based on the applicable intermolecular forces present in each compound, explain this trend in melting points.
- Solution
-
Experimentally, as the chloride compounds make their way across the third period elements, the melting points gradually decrease. This may appear an easy question to address since the melting points are a also measure of the magnitude of the intermolecular forces as play in the specific system, however it a quite complicated and to answer properly require knowledge of the chloride compounds.
Both (\(\ce{NaCl}\) and \(\ce{MgCl_2}\)) are both "ionic solids" with strong ion-ion bonding and hence have the highest melting temperatures in the comparative series. We would expect the \(\ce{Na+}\) ions in (\(\ce{NaCl}\) to have weaker Coulombic interactions than the \(\ce{Mg^{2+}}\) ions in \(\ce{MgCl_2}\) since the latter are smaller and double the charge (i.e., a higher charge density). That would make the lattice energy higher because it would generate stronger ionic bonds (lattice energy of \(\ce{NaCl}\) and \(\ce{MgCl2}\) are 876 and 2526 kJ/mol). However, this ionic perspective is insufficient to explain the observed melting points with (\(\ce{NaCl} > \ce{MgCl_2}\)), which we ascribe to bonding never being 100% ionic. As expected for teh difference in electronegativity of chlorine, magnesium, and sodium, the percent ionic character of the \(\ce{Na-Cl}\) bond is 71% and for \(\ce{Mg-Cl}\) is even lower, at 58%. Hence, the \(\ce{Na-Cl}\) bond is 29% covalent and the \(\ce{Mg-Cl}\) bond is 42% covalent. The covalent character reduces the melting point of \(\ce{MgCl2}\), even though \(\ce{Mg+}\) has a higher charge-to-size ratio than \(\ce{Na+}\).
\(\ce{AlCl_3}\) is a molecular framework solid which means the solid is an extended covalent molecule and not individual \(\ce{AlCl_3}\) molecules bound by intermolecular forces.

Both \(\ce{SiCl_4}\) and \(\ce{PCl_4}\) solids are molecular in nature. To understand the strength of intermolecular forces as play this properly, we need to apply basic VESPR rules to identify the structures of these molecules.
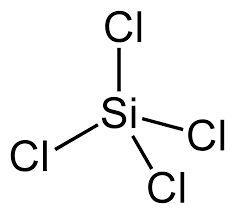
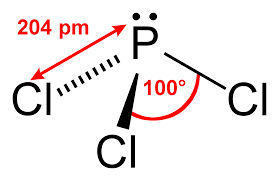
\(\ce{SiCl_4}\) is a tetrahedral molecule with no dipole moment (nor quadrupole moment either). \(\ce{PCl_4}\) is trigonal pyramidal and since \(\ce{P}\) has a different electronegativity than \(\ce{Cl}\), it has a dipole moment (0.97D). From this argument, we would think that \(\ce{PCl_4}\) would have a higher melting point, however both molecules have dispersive forces (London) too. Since the magnitude of dispersive forces increased wtih larger molecules (with more electrons to shift around), this is higher in \(\ce{PCl_4}\), which beats out the weak dipole-dipole interactions in \(\ce{PCl_4}\).
Q.71
Why are the melting points of \(\ce{NaCl}\) (801 °C) and \(\ce{MgCl_2}\) (714 °C) so much higher than the melting points of \(\ce{SCl_2}\) (-122 °C) and \(\ce{Cl_2}\) (-101.5 °C)? Explain answer in terms of intermolecular forces and identify any potential forces involved.
- Solution
-
As with all bulk properties, the melting points are a measure of the magnitude of the intermolecular forces as play in the specific system (geometric structures also affects bulk properties like the nature of the crystal lattice, but that is a secondary issue). From inspection, it is clear that the \(\ce{NaCl}\) and \(\ce{MgCl2}\) are ionic held together the strongest permanent electrostatic interaction (charge-charge or monopole-monopole); these are ionic solids. For \(\ce{SCl2}\) and \(\ce{Cl_2}\), the solid is a molecular solid wtih constituent molecules that lack charge and even dipole (easy to tell for \(\ce{Cl2}\) and requires a little VSEPR effort for \(\ce{SCl2}\). Hence, the next higher permanent electrostatic interactions are active in these molecules (i.e. quadrupole-quadrupole) along with dispersion and repulsive interactions; all of which are much weaker than the charge-charge interactions in \(\ce{NaCl}\) and \(\ce{MgCl2}\). The weaker the interactions, the lower the boiling point since less thermal energy is needed to break those interactions.
Now, a more advanced question is to explain the origin of the differences in the melting points of \(\ce{NaCl}\) vs. \(\ce{MgCl2}\). Also to explain the origin of the differences in the melting points of \(\ce{SCl2}\) vs. \(\ce{Cl2}\). No answer given.

