3.2: Intermolecular Forces - Origins in Molecular Structure
- Last updated
- Save as PDF
- Page ID
- 43104
Learning Objectives
- To describe the intermolecular forces in liquids.
The properties of liquids are intermediate between those of gases and solids, but are more similar to solids. In contrast to intramolecular forces, such as the covalent bonds that hold atoms together in molecules and polyatomic ions, intermolecular forces hold molecules together in a liquid or solid. Intermolecular forces are generally much weaker than covalent bonds. For example, it requires 927 kJ to overcome the intramolecular forces and break both O–H bonds in 1 mol of water, but it takes only about 41 kJ to overcome the intermolecular attractions and convert 1 mol of liquid water to water vapor at 100°C. (Despite this seemingly low value, the intermolecular forces in liquid water are among the strongest such forces known!) Given the large difference in the strengths of intra- and intermolecular forces, changes between the solid, liquid, and gaseous states almost invariably occur for molecular substances without breaking covalent bonds.
The properties of liquids are intermediate between those of gases and solids but are more similar to solids.
Intermolecular forces determine bulk properties such as the melting points of solids and the boiling points of liquids. Liquids boil when the molecules have enough thermal energy to overcome the intermolecular attractive forces that hold them together, thereby forming bubbles of vapor within the liquid. Similarly, solids melt when the molecules acquire enough thermal energy to overcome the intermolecular forces that lock them into place in the solid.
Coulombic Interactions
Through various experiments, Charles Augustin de Coulomb found a way to explain the interactions between charged particles, which in turn helped to explain where the stabilities and instabilities of various particles come from. While the entities that hold atoms together within a molecule can be attributed to bonds, the forces that create these bonds can be explained by Coulomb Forces. Thus, the physical basis behind the bonding of two atoms can be explained.
Coulomb’s findings indicate that like charges repel each other and unlike charges attract one another. Thus electrons, which are negatively charged, repel each other but attract protons. Likewise, protons repel each other.
Each atom is made up of a nucleus in the center, which consists of a number of protons and neutrons, depending upon the element in question. Surrounding the nucleus are electrons that float around the nucleus in what can be thought of as a cloud. As two atoms approach one another, the protons of one atom attract the electrons of the other atom. Similarly, the protons of the other atom attract the electrons of the first atom. As a result, the simultaneous attraction of the components from one atom to another create a bond. This interaction can be summarized mathematically and is known as Coulombic forces:
\[ F = k \dfrac{q_{1}q_{2}}{r^{2}} \label{C}\]
In this mathematical representation of Coulomb's observations,
- \(F\) is the electrical force acting between two atoms
- with \(q_1\) and \(q_2\) representing the magnitude of the charges of each atom,
- \(r\) is the distance between the two atoms.
- and \(k\) is a constant.
From Equation \ref{C}, the electrostatic force between two charges is inversely proportional to the square of the distance separating the two atoms.
Ion–Ion Interactions
The interactions between ions (ion - ion interactions or charge-charge interactions) are the easiest to understand since such interactions are just a simple application of Coulombic forces (Equation \ref{C}). This specific interaction operates over relatively long distances in the gas phase and is responsible for the attraction of opposite charge ions and the repulsion of like charged ions.
Coulombic forces are also involved in all forms of chemical bonding; when they act between separate charged particles they are especially strong. Thus the energy required to pull a mole of \(\ce{Na^{+}}\) and \(\ce{F^{–}}\) ions apart in the sodium fluoride crystal is greater than that needed to break the a covalent bonds of a mole of \(\ce{H2}\). The effects of ion-ion attraction are seen most directly in salts such as \(\ce{NaF}\) and \(\ce{NaCl}\) that consist of oppositely-charged ions arranged in inter-penetrating crystal lattices.
According to Coulomb's Law the force between two charged particles is given by
\[ \underbrace{F= \dfrac{q_1q_2}{4\pi\epsilon_0 r^2}}_{\text{ion-ion Force}} \label{7.2.1}\]
Instead of using SI units, chemists often prefer to express atomic-scale distances in picometers and charges as electron charge (±1, ±2, etc.) Using these units, the proportionality constant \(1/4\pi\epsilon\) works out to \(2.31 \times 10^{16}\; J\; pm\). The sign of \(F\) determines whether the force will be attractive (–) or repulsive (+); notice that the latter is the case whenever the two q's have the same sign. Two oppositely-charged particles flying about in a vacuum will be attracted toward each other, and the force becomes stronger and stronger as they approach until eventually they will stick together and a considerable amount of energy will be required to separate them.

They form an ion-pair, a new particle which has a positively-charged area and a negatively-charged area. There are fairly strong interactions between these ion pairs and free ions, so that these clusters tend to grow, and they will eventually fall out of the gas phase as a liquid or solid (depending on the temperature).
Equation \ref{7.2.1} is an example of an inverse square law; the force falls off as the square of the distance. A similar law governs the manner in which the illumination falls off as you move away from a point light source; recall this the next time you walk away from a street light at night, and you will have some feeling for what an inverse square law means.
The stronger the attractive force acting between two particles, the greater the amount of work required to separate them. Work represents a flow of energy, so the foregoing statement is another way of saying that when two particles move in response to a force, their potential energy is lowered. This work is found by integrating the negative of the force function with respect to distance over the distance moved. Thus the energy that must be supplied in order to completely separate two oppositely-charged particles initially at a distance \(r_0\) is given by
\[ w= - \int _{r_o} ^{\infty} \dfrac{q_1q_2}{4\pi\epsilon_0 r^2}dr = - \dfrac{q_1q_2}{4\pi\epsilon_0 r_o} \label{7.2.2}\]
hence, the potential (\(V_{ion-ion}\)) responsible for the ion-ion force is
\[ \underbrace{V_{ion-ion} = \dfrac{q_1q_2}{4\pi\epsilon_0 r} }_{\text{ion-ion potential}} \label{7.2.3}\]
Example \(\PageIndex{1}\)
When sodium chloride is melted, some of the ion pairs vaporize and form neutral \(\ce{NaCl}\) dimers. How much energy would be released when one mole of \(\ce{Na^{+}}\) and \(\ce{Cl^{–}}\) ions are brought together to generate dimers in this way? The bondlength of \(\ce{NaCl}\) is 237 pm.
Solution
The interactions involved in forming \(\ce{NaCl}\) dimers is the ion-ion forces with a potential energy given by Equation \ref{7.2.3}. However, this is the energy of interaction for one pair of \(\ce{Na^{+}}\) and \(\ce{Cl^{–}}\) ion and needs to be scaled by a mole. So the energy released will be
\[\begin{align*}E &= N_a V(\ce{NaCl}) \\[4pt] &= N_a\dfrac{q_1q_2}{4\pi\epsilon_0 r} \end{align*}\]
The \(r\) in this equation is the distance between the two ions, which is the bondlength of 237 pm (\(237 \times 10^{-12}m\)).
\[\begin{align*}E &= (6.022 \times 10^{23} ) \underbrace{(8.987 \times 10^9 N m^2/C^2 )}_{1/4\pi\epsilon_o} \dfrac{(+1.6 \times 10^{-19}C) (-1.6 \times 10^{-19}C) }{ 237 \times 10^{-12} m} \\[4pt] &= –584 \;kJ/mol \end{align*}\]
This is not the energy needed to separate one mole of NaCl since that is a lattice and has more than pairwise interactions and require addressing the geometric orientation of the lattice (see Madelung Constants for more details).
Intermolecular forces are electrostatic in nature; that is, they arise from the electrostatic interaction between positively and negatively charged species. Like covalent and ionic bonds, intermolecular interactions are the sum of both attractive and repulsive components. Because electrostatic interactions fall off rapidly with increasing distance between molecules, intermolecular interactions are most important for solids and liquids, where the molecules are close together. These interactions become important for gases only at very high pressures, where they are responsible for the observed deviations from the ideal gas law at high pressures (i.e., real gases).
Ion-Dipole Interactions
A dipole that is close to a positive or negative ion will orient itself so that the end whose partial charge is opposite to the ion charge will point toward the ion. This kind of interaction is very important in aqueous solutions of ionic substances; H2O is a highly polar molecule, so that in a solution of sodium chloride, for example, the Na+ ions will be enveloped by a shell of water molecules with their oxygen-ends pointing toward these ions, while H2O molecules surrounding the Cl– ions will have their hydrogen ends directed inward. As a consequence of ion-dipole interactions, all ionic species in aqueous solution are hydrated; this is what is denoted by the suffix in formulas such as K+(aq), etc.
The strength of ion-dipole attraction depends on the magnitude of the dipole moment and on the charge density of the ion. This latter quantity is just the charge of the ion divided by its volume. Owing to their smaller sizes, positive ions tend to have larger charge densities than negative ions, and they should be more strongly hydrated in aqueous solution. The hydrogen ion, being nothing more than a bare proton of extremely small volume, has the highest charge density of any ion; it is for this reason that it exists entirely in its hydrated form H3O+ in water.
Since there is now both attractive and repulsive interactions and they both get weaker as the ion and dipole distance increases while also approaching each other in strength, the net ion-dipole is an inverse square relationship as shown in Equation \ref{11.2.2}.
\[ \underbrace{ E\: \propto \: \dfrac{-|q_1|\mu_2}{r^2}}_{\text{ion-dipole potential}} \label{11.2.2}\]
- \(r\) is the distance of separation.
- \(q\) is the charge of the ion ( only the magnitude of the charge is shown here.)
- \(\mu\) is the permanent dipole moment of the polar molecule. \[ \vec{\mu} = q' \, \vec{d} \label{11.2.3}\] where \(q'\) is the partial charge of each end of the dipole and \(d\) is the separation between the charges within the dipole
Ion-Ion vs. Ion-Dipole potentials
There are several differences between ion-ion potential (Equation \ref{7.2.3}) and the ion-dipole potential (Equation \ref{11.2.2}) interactions.
- First, the potential of ion/dipole interactions are negative and net interaction will always be attractive, since the attraction of the opposite dipole to the ion will make it closer than the dipole with the like charge. By using the absolute value of the charge of the ion, and placing a negative sign in front of the equation, this results in a lowering of the potential energy (\(\mu\) is positive).
- Second, the potential drops off quicker in Equation \ref{11.2.2}, where it is an inverse square relationship to the radius (\(1/r^2\)), while a simple charge-charge interaction (Equation \ref{7.2.3}) has a linear inverse relationship (\(1/r\)). This means the ion-dipole are a shorter range interaction and diminish more rapidly the father the polar molecule is from the ion.
- Third, note that the units of the two equations are the same, as \(\mu\) has the units of charge X distance. However, the distance in \(\mu\) is the distance between the dipoles of the polar molecule, while the distance denoted by the "r" is the distance between the ion and the dipole.
It needs to be understood that the molecules in a solution are rotating and vibrating and actual systems are quite complicated (Figure \(\PageIndex{4}\)). What is important to realize is that these interactions are Coulombic in nature and how the mathematical equations describe this in terms of the magnitude of the charges and their distances from each other. In this course we will not be calculating dipole moments or the magnitudes of them, but understanding how to read the equations, and developing qualitative understandings that allow us to predict trends.

Dipole–Dipole Interactions
Polar covalent bonds behave as if the bonded atoms have localized fractional charges that are equal but opposite (i.e., the two bonded atoms generate a dipole). If the structure of a molecule is such that the individual bond dipoles do not cancel one another, then the molecule has a net dipole moment. Molecules with net dipole moments tend to align themselves so that the positive end of one dipole is near the negative end of another and vice versa, as shown in part (a) in Figure \(\PageIndex{1}\).
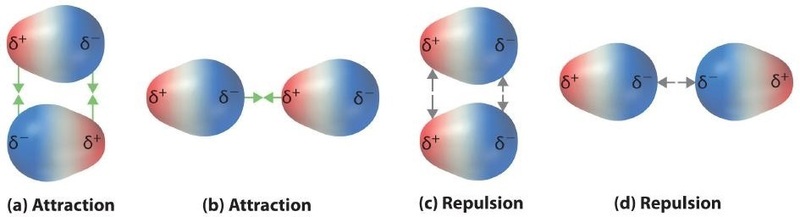
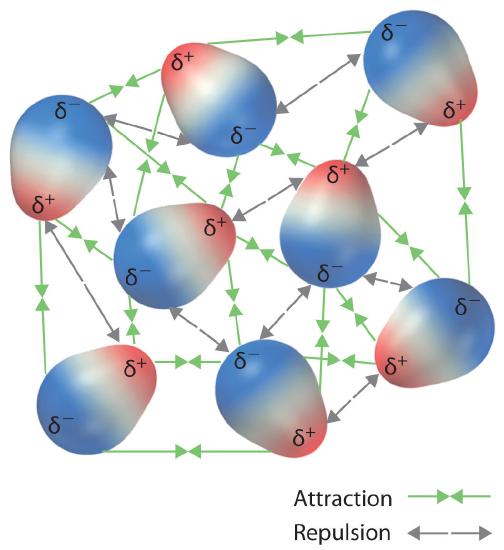
These arrangements are more stable than arrangements in which two positive or two negative ends are adjacent (Figure \(\PageIndex{1c}\)). Hence dipole–dipole interactions, such as those in Figure \(\PageIndex{5b}\), are attractive intermolecular interactions, whereas those in Figure \(\PageIndex{5d}\) are repulsive intermolecular interactions. Because molecules in a liquid move freely and continuously, molecules always experience both attractive and repulsive dipole–dipole interactions simultaneously, as shown in Figure \(\PageIndex{2}\). On average, however, the attractive interactions dominate.
Because each end of a dipole possesses only a fraction of the charge of an electron, dipole–dipole interactions are substantially weaker than the interactions between two ions, each of which has a charge of at least ±1, or between a dipole and an ion, in which one of the species has at least a full positive or negative charge. In addition, the attractive interaction between dipoles falls off much more rapidly with increasing distance than do the ion–ion interactions. Recall that the attractive energy between two ions is proportional to 1/r, where r is the distance between the ions. Doubling the distance (r → 2r) decreases the attractive energy by one-half.
In contrast, the energy of the interaction of two dipoles is proportional to 1/r6, so doubling the distance between the dipoles decreases the strength of the interaction by 26, or 64-fold:
\[V=-\dfrac{2\mu_{A}^2\mu_{B}^2}{3(4\pi\epsilon_{0})^2r^6}\dfrac{1}{k_{B}T} \label{5}\]
Thus a substance such as HCl, which is partially held together by dipole–dipole interactions, is a gas at room temperature and 1 atm pressure, whereas NaCl, which is held together by interionic interactions, is a high-melting-point solid. Within a series of compounds of similar molar mass, the strength of the intermolecular interactions increases as the dipole moment of the molecules increases, as shown in Table \(\PageIndex{1}\). Using what we learned about predicting relative bond polarities from the electronegativities of the bonded atoms, we can make educated guesses about the relative boiling points of similar molecules.
| Compound | Molar Mass (g/mol) | Dipole Moment (D) | Boiling Point (K) |
|---|---|---|---|
| C3H6 (cyclopropane) | 42 | 0 | 240 |
| CH3OCH3 (dimethyl ether) | 46 | 1.30 | 248 |
| CH3CN (acetonitrile) | 41 | 3.9 | 355 |
The attractive energy between two ions is proportional to 1/r, whereas the attractive energy between two dipoles is proportional to 1/r6.
Example \(\PageIndex{2}\)
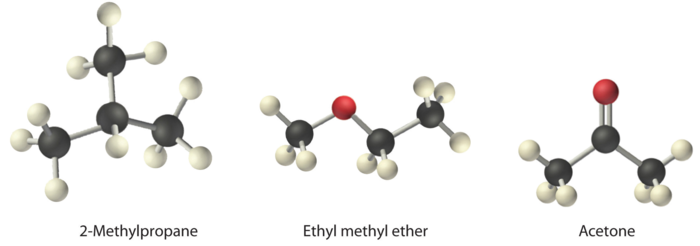
Arrange ethyl methyl ether (\(\ce{CH3OCH2CH3}\)), 2-methylpropane [isobutane, \(\ce{(CH3)2CHCH3}\)], and acetone (\(\ce{CH3COCH3}\)) in order of increasing boiling points. Their structures are as follows:
Given: compounds
Asked for: order of increasing boiling points
Strategy:
Compare the molar masses and the polarities of the compounds. Compounds with higher molar masses and that are polar will have the highest boiling points.
Solution:
The three compounds have essentially the same molar mass (58–60 g/mol), so we must look at differences in polarity to predict the strength of the intermolecular dipole–dipole interactions and thus the boiling points of the compounds. The first compound, 2-methylpropane, contains only C–H bonds, which are not very polar because C and H have similar electronegativities. It should therefore have a very small (but nonzero) dipole moment and a very low boiling point. Ethyl methyl ether has a structure similar to H2O; it contains two polar C–O single bonds oriented at about a 109° angle to each other, in addition to relatively nonpolar C–H bonds. As a result, the C–O bond dipoles partially reinforce one another and generate a significant dipole moment that should give a moderately high boiling point. Acetone contains a polar C=O double bond oriented at about 120° to two methyl groups with nonpolar C–H bonds. The C–O bond dipole therefore corresponds to the molecular dipole, which should result in both a rather large dipole moment and a high boiling point. Thus we predict the following order of boiling points: 2-methylpropane < ethyl methyl ether < acetone. This result is in good agreement with the actual data: 2-methylpropane, boiling point = −11.7°C, and the dipole moment (μ) = 0.13 D; methyl ethyl ether, boiling point = 7.4°C and μ = 1.17 D; acetone, boiling point = 56.1°C and μ = 2.88 D.
Exercise \(\PageIndex{1}\)
Arrange carbon tetrafluoride (CF4), ethyl methyl sulfide (CH3SC2H5), dimethyl sulfoxide [(CH3)2S=O], and 2-methylbutane [isopentane, (CH3)2CHCH2CH3] in order of decreasing boiling points.
- Answer
-
dimethyl sulfoxide (boiling point = 189.9°C) > ethyl methyl sulfide (boiling point = 67°C) > 2-methylbutane (boiling point = 27.8°C) > carbon tetrafluoride (boiling point = −128°C)
London Dispersion Forces
Thus far we have considered only interactions between polar molecules, but other factors must be considered to explain why many nonpolar molecules, such as bromine, benzene, and hexane, are liquids at room temperature, and others, such as iodine and naphthalene, are solids. Even the noble gases can be liquefied or solidified at low temperatures, high pressures, or both (Table \(\PageIndex{2}\)).
What kind of attractive forces can exist between nonpolar molecules or atoms? This question was answered by Fritz London (1900–1954), a German physicist who later worked in the United States. In 1930, London proposed that temporary fluctuations in the electron distributions within atoms and nonpolar molecules could result in the formation of short-lived instantaneous dipole moments, which produce attractive forces called London dispersion forces between otherwise nonpolar substances.
| Substance | Molar Mass (g/mol) | Melting Point (°C) | Boiling Point (°C) |
|---|---|---|---|
| Ar | 40 | −189.4 | −185.9 |
| Xe | 131 | −111.8 | −108.1 |
| N2 | 28 | −210 | −195.8 |
| O2 | 32 | −218.8 | −183.0 |
| F2 | 38 | −219.7 | −188.1 |
| I2 | 254 | 113.7 | 184.4 |
| CH4 | 16 | −182.5 | −161.5 |
Consider a pair of adjacent He atoms, for example. On average, the two electrons in each He atom are uniformly distributed around the nucleus. Because the electrons are in constant motion, however, their distribution in one atom is likely to be asymmetrical at any given instant, resulting in an instantaneous dipole moment. As shown in part (a) in Figure \(\PageIndex{3}\), the instantaneous dipole moment on one atom can interact with the electrons in an adjacent atom, pulling them toward the positive end of the instantaneous dipole or repelling them from the negative end. The net effect is that the first atom causes the temporary formation of a dipole, called an induced dipole, in the second. Interactions between these temporary dipoles cause atoms to be attracted to one another. These attractive interactions are weak and fall off rapidly with increasing distance. London was able to show with quantum mechanics that the attractive energy between molecules due to temporary dipole–induced dipole interactions falls off as 1/r6. Doubling the distance therefore decreases the attractive energy by 26, or 64-fold.
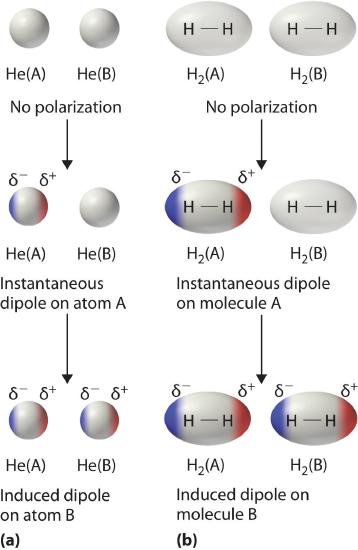
Instantaneous dipole–induced dipole interactions between nonpolar molecules can produce intermolecular attractions just as they produce interatomic attractions in monatomic substances like Xe. This effect, illustrated for two H2 molecules in part (b) in Figure \(\PageIndex{3}\), tends to become more pronounced as atomic and molecular masses increase (Table \(\PageIndex{2}\)). For example, Xe boils at −108.1°C, whereas He boils at −269°C. The reason for this trend is that the strength of London dispersion forces is related to the ease with which the electron distribution in a given atom can be perturbed. In small atoms such as He, the two 1s electrons are held close to the nucleus in a very small volume, and electron–electron repulsions are strong enough to prevent significant asymmetry in their distribution. In larger atoms such as Xe, however, the outer electrons are much less strongly attracted to the nucleus because of filled intervening shells. As a result, it is relatively easy to temporarily deform the electron distribution to generate an instantaneous or induced dipole. The ease of deformation of the electron distribution in an atom or molecule is called its polarizability. Because the electron distribution is more easily perturbed in large, heavy species than in small, light species, we say that heavier substances tend to be much more polarizable than lighter ones.
For similar substances, London dispersion forces get stronger with increasing molecular size.
The polarizability of a substance also determines how it interacts with ions and species that possess permanent dipoles. Thus London dispersion forces are responsible for the general trend toward higher boiling points with increased molecular mass and greater surface area in a homologous series of compounds, such as the alkanes (part (a) in Figure \(\PageIndex{4}\)). The strengths of London dispersion forces also depend significantly on molecular shape because shape determines how much of one molecule can interact with its neighboring molecules at any given time. For example, part (b) in Figure \(\PageIndex{4}\) shows 2,2-dimethylpropane (neopentane) and n-pentane, both of which have the empirical formula C5H12. Neopentane is almost spherical, with a small surface area for intermolecular interactions, whereas n-pentane has an extended conformation that enables it to come into close contact with other n-pentane molecules. As a result, the boiling point of neopentane (9.5°C) is more than 25°C lower than the boiling point of n-pentane (36.1°C).
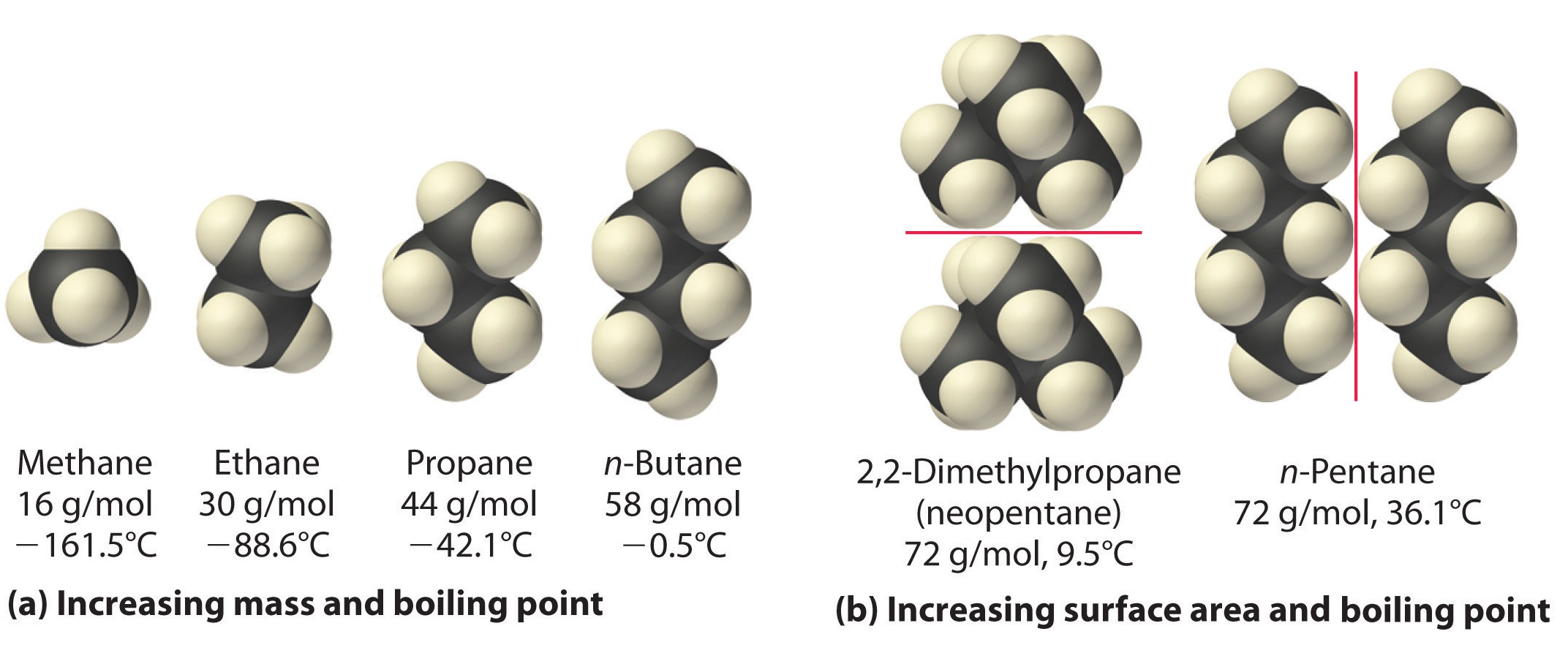
All molecules, whether polar or nonpolar, are attracted to one another by London dispersion forces in addition to any other attractive forces that may be present. In general, however, dipole–dipole interactions in small polar molecules are significantly stronger than London dispersion forces, so the former predominate.
Example \(\PageIndex{2}\)
Arrange n-butane, propane, 2-methylpropane [isobutene, (CH3)2CHCH3], and n-pentane in order of increasing boiling points.
Given: compounds
Asked for: order of increasing boiling points
Strategy:
Determine the intermolecular forces in the compounds and then arrange the compounds according to the strength of those forces. The substance with the weakest forces will have the lowest boiling point.
Solution:
The four compounds are alkanes and nonpolar, so London dispersion forces are the only important intermolecular forces. These forces are generally stronger with increasing molecular mass, so propane should have the lowest boiling point and n-pentane should have the highest, with the two butane isomers falling in between. Of the two butane isomers, 2-methylpropane is more compact, and n-butane has the more extended shape. Consequently, we expect intermolecular interactions for n-butane to be stronger due to its larger surface area, resulting in a higher boiling point. The overall order is thus as follows, with actual boiling points in parentheses: propane (−42.1°C) < 2-methylpropane (−11.7°C) < n-butane (−0.5°C) < n-pentane (36.1°C).
Exercise \(\PageIndex{2}\)
Arrange GeH4, SiCl4, SiH4, CH4, and GeCl4 in order of decreasing boiling points.
- Answer
-
GeCl4 (87°C) > SiCl4 (57.6°C) > GeH4 (−88.5°C) > SiH4 (−111.8°C) > CH4 (−161°C)
Summary
Intermolecular forces are electrostatic in nature and include van der Waals forces and hydrogen bonds. Molecules in liquids are held to other molecules by intermolecular interactions, which are weaker than the intramolecular interactions that hold the atoms together within molecules and polyatomic ions. Transitions between the solid and liquid or the liquid and gas phases are due to changes in intermolecular interactions but do not affect intramolecular interactions. The three major types of intermolecular interactions are dipole–dipole interactions, London dispersion forces (these two are often referred to collectively as van der Waals forces), and hydrogen bonds. Dipole–dipole interactions arise from the electrostatic interactions of the positive and negative ends of molecules with permanent dipole moments; their strength is proportional to the magnitude of the dipole moment and to 1/r6, where r is the distance between dipoles. London dispersion forces are due to the formation of instantaneous dipole moments in polar or nonpolar molecules as a result of short-lived fluctuations of electron charge distribution, which in turn cause the temporary formation of an induced dipole in adjacent molecules. Like dipole–dipole interactions, their energy falls off as 1/r6. Larger atoms tend to be more polarizable than smaller ones because their outer electrons are less tightly bound and are therefore more easily perturbed.

