2.7: The Third Law of Thermodynamics
- Last updated
- Save as PDF
- Page ID
- 46428
Learning Objectives
- The absolute entropy of a pure substance at a given temperature is the sum of all the entropy it would acquire on warming from absolute zero (where \(S=0\)) to the particular temperature.
- Calculate entropy changes for phase transitions and chemical reactions under standard conditions
The atoms, molecules, or ions that compose a chemical system can undergo several types of molecular motion, including translation, rotation, and vibration (Figure \(\PageIndex{1}\)). The greater the molecular motion of a system, the greater the number of possible microstates and the higher the entropy. A perfectly ordered system with only a single microstate available to it would have an entropy of zero. The only system that meets this criterion is a perfect crystal at a temperature of absolute zero (0 K), in which each component atom, molecule, or ion is fixed in place within a crystal lattice and exhibits no motion (ignoring quantum zero point motion).
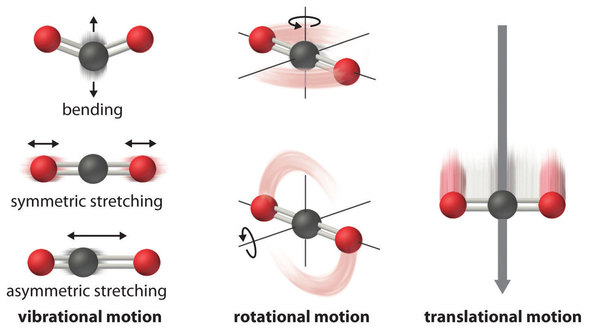
This system may be described by a single microstate, as its purity, perfect crystallinity and complete lack of motion (at least classically, quantum mechanics argues for constant motion) means there is but one possible location for each identical atom or molecule comprising the crystal (\(\Omega = 1\)). According to the Boltzmann equation, the entropy of this system is zero.
\[\begin{align*} S&=k\ln \Omega \\[4pt] &= k\ln(1) \\[4pt] &=0 \label{\(\PageIndex{5}\)} \end{align*}\]
In practice, absolute zero is an ideal temperature that is unobtainable, and a perfect single crystal is also an ideal that cannot be achieved. Nonetheless, the combination of these two ideals constitutes the basis for the third law of thermodynamics: the entropy of any perfectly ordered, crystalline substance at absolute zero is zero.
Definition: Third Law of Thermodynamics
The entropy of a pure, perfect crystalline substance at 0 K is zero.
The third law of thermodynamics has two important consequences: it defines the sign of the entropy of any substance at temperatures above absolute zero as positive, and it provides a fixed reference point that allows us to measure the absolute entropy of any substance at any temperature. In this section, we examine two different ways to calculate ΔS for a reaction or a physical change. The first, based on the definition of absolute entropy provided by the third law of thermodynamics, uses tabulated values of absolute entropies of substances. The second, based on the fact that entropy is a state function, uses a thermodynamic cycle similar to those discussed previously.
Standard-State Entropies
One way of calculating \(ΔS\) for a reaction is to use tabulated values of the standard molar entropy (\(S^o\)), which is the entropy of 1 mol of a substance under standard pressure (1 bar). Often the standard molar entropy is given at 298 K and is often demarked as \(ΔS^o_{298}\). The units of \(S^o\) are J/(mol•K). Unlike enthalpy or internal energy, it is possible to obtain absolute entropy values by measuring the entropy change that occurs between the reference point of 0 K (corresponding to \(S = 0\)) and 298 K (Tables T1 and T2).
As shown in Table \(\PageIndex{1}\), for substances with approximately the same molar mass and number of atoms, \(S^o\) values fall in the order
\[S^o(\text{gas}) \gg S^o(\text{liquid}) > S^o(\text{solid}).\]
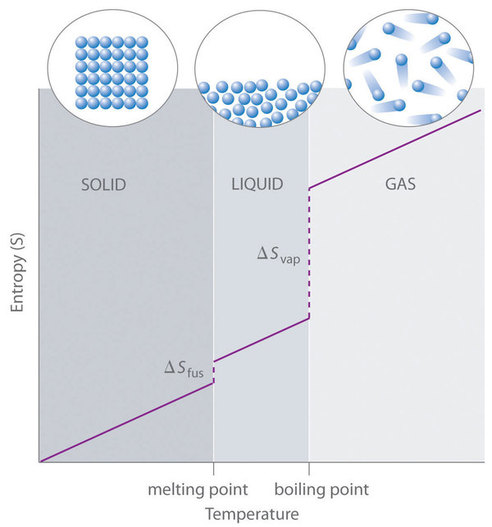
For instance, \(S^o\) for liquid water is 70.0 J/(mol•K), whereas \(S^o\) for water vapor is 188.8 J/(mol•K). Likewise, \(S^o\) is 260.7 J/(mol•K) for gaseous \(\ce{I2}\) and 116.1 J/(mol•K) for solid \(\ce{I2}\). This order makes qualitative sense based on the kinds and extents of motion available to atoms and molecules in the three phases (Figure \(\PageIndex{1}\)). The correlation between physical state and absolute entropy is illustrated in Figure \(\PageIndex{2}\), which is a generalized plot of the entropy of a substance versus temperature.
The Third Law Lets us Calculate Absolute Entropies
The absolute entropy of a substance at any temperature above 0 K must be determined by calculating the increments of heat \(q\) required to bring the substance from 0 K to the temperature of interest, and then summing the ratios \(q/T\). Two kinds of experimental measurements are needed:
- The enthalpies associated with any phase changes the substance may undergo within the temperature range of interest. Melting of a solid and vaporization of a liquid correspond to sizeable increases in the number of microstates available to accept thermal energy, so as these processes occur, energy will flow into a system, filling these new microstates to the extent required to maintain a constant temperature (the freezing or boiling point); these inflows of thermal energy correspond to the heats of fusion and vaporization. The entropy increase associated with transition at temperature \(T\) is \[ \dfrac{ΔH_{fusion}}{T}.\]
- The heat capacity \(C\) of a phase expresses the quantity of heat required to change the temperature by a small amount \(ΔT\), or more precisely, by an infinitesimal amount \(dT\). Thus the entropy increase brought about by warming a substance over a range of temperatures that does not encompass a phase transition is given by the sum of the quantities \(C \frac{dT}{T}\) for each increment of temperature \(dT\). This is of course just the integral
\[ S_{0 \rightarrow T} = \int _{0}^{T} \dfrac{C_p}{T} dt \label{eq20}\]
Because the heat capacity is itself slightly temperature dependent, the most precise determinations of absolute entropies require that the functional dependence of \(C\) on \(T\) be used in the integral in Equation \ref{eq20}, i.e.,:
\[ S_{0 \rightarrow T} = \int _{0}^{T} \dfrac{C_p(T)}{T} dt. \label{eq21}\]
When this is not known, one can take a series of heat capacity measurements over narrow temperature increments \(ΔT\) and measure the area under each section of the curve. The area under each section of the plot represents the entropy change associated with heating the substance through an interval \(ΔT\). To this must be added the enthalpies of melting, vaporization, and of any solid-solid phase changes.
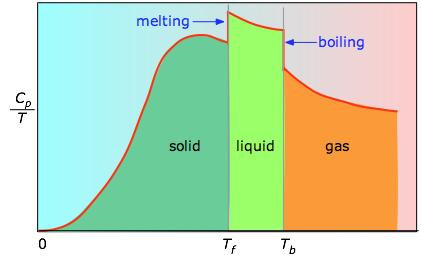
Values of \(C_p\) for temperatures near zero are not measured directly, but can be estimated from quantum theory. The cumulative areas from 0 K to any given temperature (Figure \(\PageIndex{3}\)) are then plotted as a function of \(T\), and any phase-change entropies such as
\[S_{vap} = \dfrac{H_{vap}}{T_b}\]
are added to obtain the absolute entropy at temperature \(T\). As shown in Figure \(\PageIndex{2}\) above, the entropy of a substance increases with temperature, and it does so for two reasons:
- As the temperature rises, more microstates become accessible, allowing thermal energy to be more widely dispersed. This is reflected in the gradual increase of entropy with temperature.
- The molecules of solids, liquids, and gases have increasingly greater freedom to move around, facilitating the spreading and sharing of thermal energy. Phase changes are therefore accompanied by massive and discontinuous increase in the entropy.
Calculating \(\Delta S_{sys}\)
We can make careful calorimetric measurements to determine the temperature dependence of a substance’s entropy and to derive absolute entropy values under specific conditions. Standard entropies are given the label \(S^o_{298}\) for values determined for one mole of substance at a pressure of 1 bar and a temperature of 298 K. The standard entropy change (\(ΔS^o\)) for any process may be computed from the standard entropies of its reactant and product species like the following:
\[ΔS^o=\sum νS^o_{298}(\ce{products})−\sum νS^o_{298}(\ce{reactants}) \label{\(\PageIndex{6}\)}\]
Here, \(ν\) represents stoichiometric coefficients in the balanced equation representing the process. For example, \(ΔS^o\) for the following reaction at room temperature
is computed as the following:
\[ΔS^o=[xS^o_{298}(\ce{C})+yS^o_{298}(\ce{D})]−[mS^o_{298}(\ce{A})+nS^o_{298}(\ce{B})] \label{\(\PageIndex{8}\)}\]
Table \(\PageIndex{1}\) lists some standard entropies at 298.15 K. You can find additional standard entropies in Tables T1 and T2
| Gases | Liquids | Solids | |||
|---|---|---|---|---|---|
| Substance | \(S^o\) [J/(mol•K)] | Substance | \(S^o\) [J/(mol•K)] | Substance | \(S^o\) [J/(mol•K)] |
| He | 126.2 | H2O | 70.0 | C (diamond) | 2.4 |
| H2 | 130.7 | CH3OH | 126.8 | C (graphite) | 5.7 |
| Ne | 146.3 | Br2 | 152.2 | LiF | 35.7 |
| Ar | 154.8 | CH3CH2OH | 160.7 | SiO2 (quartz) | 41.5 |
| Kr | 164.1 | C6H6 | 173.4 | Ca | 41.6 |
| Xe | 169.7 | CH3COCl | 200.8 | Na | 51.3 |
| H2O | 188.8 | C6H12 (cyclohexane) | 204.4 | MgF2 | 57.2 |
| N2 | 191.6 | C8H18 (isooctane) | 329.3 | K | 64.7 |
| O2 | 205.2 | NaCl | 72.1 | ||
| CO2 | 213.8 | KCl | 82.6 | ||
| I2 | 260.7 | I2 | 116.1 | ||
A closer examination of Table \(\PageIndex{1}\) also reveals that substances with similar molecular structures tend to have similar \(S^o\) values. Among crystalline materials, those with the lowest entropies tend to be rigid crystals composed of small atoms linked by strong, highly directional bonds, such as diamond (\(S^o = 2.4 \,J/(mol•K)\)). In contrast, graphite, the softer, less rigid allotrope of carbon, has a higher \(S^o\) (5.7 J/(mol•K)) due to more disorder (microstates) in the crystal. Soft crystalline substances and those with larger atoms tend to have higher entropies because of increased molecular motion and disorder. Similarly, the absolute entropy of a substance tends to increase with increasing molecular complexity because the number of available microstates increases with molecular complexity. For example, compare the \(S^o\) values for CH3OH(l) and CH3CH2OH(l). Finally, substances with strong hydrogen bonds have lower values of \(S^o\), which reflects a more ordered structure.
Entropy increases with softer, less rigid solids, solids that contain larger atoms, and solids with complex molecular structures.
To calculate \(ΔS^o\) for a chemical reaction from standard molar entropies, we use the familiar “products minus reactants” rule, in which the absolute entropy of each reactant and product is multiplied by its stoichiometric coefficient in the balanced chemical equation. Example \(\PageIndex{1}\) illustrates this procedure for the combustion of the liquid hydrocarbon isooctane (\(\ce{C8H18}\); 2,2,4-trimethylpentane).
Example \(\PageIndex{1}\)
Use the data in Table \(\PageIndex{1}\) to calculate \(ΔS^o\) for the reaction of liquid isooctane with \(\ce{O2(g)}\) to give \(\ce{CO2(g)}\) and \(\ce{H2O(g)}\) at 298 K.
Given: standard molar entropies, reactants, and products
Asked for: ΔS°
Strategy:
Write the balanced chemical equation for the reaction and identify the appropriate quantities in Table \(\PageIndex{1}\). Subtract the sum of the absolute entropies of the reactants from the sum of the absolute entropies of the products, each multiplied by their appropriate stoichiometric coefficients, to obtain \(ΔS^o\) for the reaction.
Solution:
The balanced chemical equation for the complete combustion of isooctane (\(\ce{C8H18}\)) is as follows:
\[\ce{C8H18(l) + 25/2 O2(g) -> 8CO2(g) + 9H2O(g)} \nonumber\]
We calculate \(ΔS^o\) for the reaction using the “products minus reactants” rule, where m and n are the stoichiometric coefficients of each product and each reactant:
\[\begin{align*}\Delta S^o_{\textrm{rxn}}&=\sum mS^o(\textrm{products})-\sum nS^o(\textrm{reactants})
\\[4pt] &=[8S^o(\mathrm{CO_2})+9S^o(\mathrm{H_2O})]-[S^o(\mathrm{C_8H_{18}})+\dfrac{25}{2}S^o(\mathrm{O_2})]
\\[4pt] &=\left \{ [8\textrm{ mol }\mathrm{CO_2}\times213.8\;\mathrm{J/(mol\cdot K)}]+[9\textrm{ mol }\mathrm{H_2O}\times188.8\;\mathrm{J/(mol\cdot K)}] \right \}
\\[4pt] & \,\,\, -\left \{[1\textrm{ mol }\mathrm{C_8H_{18}}\times329.3\;\mathrm{J/(mol\cdot K)}]+\left [\dfrac{25}{2}\textrm{ mol }\mathrm{O_2}\times205.2\textrm{ J}/(\mathrm{mol\cdot K})\right ] \right \}
\\[4pt] &=515.3\;\mathrm{J/K}\end{align*}\]
\(ΔS^o\) is positive, as expected for a combustion reaction in which one large hydrocarbon molecule is converted to many molecules of gaseous products.
Exercise \(\PageIndex{1}\)
Use the data in Table \(\PageIndex{1}\) to calculate \(ΔS^o\) for the reaction of \(\ce{H2(g)}\) with liquid benzene (\(\ce{C6H6}\)) to give cyclohexane (\(\ce{C6H12}\)) at 298 K.
- Answer
-
-361.1 J/K
Example \(\PageIndex{2}\): Determination of ΔS°
Calculate the standard entropy change for the following process at 298 K:
\[\ce{H2O}(g)⟶\ce{H2O}(l)\nonumber\]
Solution
The value of the standard entropy change at room temperature, \(ΔS^o_{298}\), is the difference between the standard entropy of the product, H2O(l), and the standard entropy of the reactant, H2O(g).
\[\begin{align*} ΔS^o_{298} &=S^o_{298}(\ce{H2O (l)})−S^o_{298}(\ce{H2O(g)})\nonumber \\[4pt] &= (70.0\: J\:mol^{−1}K^{−1})−(188.8\: Jmol^{−1}K^{−1})\nonumber \\[4pt] &=−118.8\:J\:mol^{−1}K^{−1} \end{align*}\]
The value for \(ΔS^o_{298}\) is negative, as expected for this phase transition (condensation), which the previous section discussed.
Exercise \(\PageIndex{2}\)
Calculate the standard entropy change for the following process at 298 K:
\[\ce{H2}(g)+\ce{C2H4}(g)⟶\ce{C2H6}(g)\nonumber\]
- Answer
-
−120.6 J mol−1 K−1
Example \(\PageIndex{3}\): Determination of ΔS°
Calculate the standard entropy change for the combustion of methanol, CH3OH at 298 K:
\[\ce{2CH3OH}(l)+\ce{3O2}(g)⟶\ce{2CO2}(g)+\ce{4H2O}(l)\nonumber\]
Solution
The value of the standard entropy change is equal to the difference between the standard entropies of the products and the entropies of the reactants scaled by their stoichiometric coefficients. The standard entropy of formations are found in Table \(\PageIndex{1}\).
\[\begin{align*} ΔS^o &=ΔS^o_{298} \\[4pt] &= ∑νS^o_{298}(\ce{products})−∑νS^o_{298} (\ce{reactants}) \\[4pt] & = 2S^o_{298}(\ce{CO2}(g))+4S^o_{298}(\ce{H2O}(l))]−[2S^o_{298}(\ce{CH3OH}(l))+3S^o_{298}(\ce{O2}(g))]\nonumber \\[4pt] &= [(2 \times 213.8) + (4×70.0)]−[ (2 \times 126.8) + (3 \times 205.03) ]\nonumber \\[4pt] &= −161.6 \:J/mol⋅K\nonumber \end{align*} \]
Exercise \(\PageIndex{3}\)
Calculate the standard entropy change for the following reaction at 298 K:
\[\ce{Ca(OH)2}(s)⟶\ce{CaO}(s)+\ce{H2O}(l)\nonumber\]
- Answer
-
24.7 J/mol•K
Summary
Energy values, as you know, are all relative, and must be defined on a scale that is completely arbitrary; there is no such thing as the absolute energy of a substance, so we can arbitrarily define the enthalpy or internal energy of an element in its most stable form at 298 K and 1 atm pressure as zero. The same is not true of the entropy; since entropy is a measure of the “dilution” of thermal energy, it follows that the less thermal energy available to spread through a system (that is, the lower the temperature), the smaller will be its entropy. In other words, as the absolute temperature of a substance approaches zero, so does its entropy. This principle is the basis of the Third law of thermodynamics, which states that the entropy of a perfectly-ordered solid at 0 K is zero.
In practice, chemists determine the absolute entropy of a substance by measuring the molar heat capacity (\(C_p\)) as a function of temperature and then plotting the quantity \(C_p/T\) versus \(T\). The area under the curve between 0 K and any temperature T is the absolute entropy of the substance at \(T\). In contrast, other thermodynamic properties, such as internal energy and enthalpy, can be evaluated in only relative terms, not absolute terms.
The second law of thermodynamics states that a spontaneous process increases the entropy of the universe, Suniv > 0. If ΔSuniv < 0, the process is nonspontaneous, and if ΔSuniv = 0, the system is at equilibrium. The third law of thermodynamics establishes the zero for entropy as that of a perfect, pure crystalline solid at 0 K. With only one possible microstate, the entropy is zero. We may compute the standard entropy change for a process by using standard entropy values for the reactants and products involved in the process.
Contributors and Attributions
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).
Stephen Lower, Professor Emeritus (Simon Fraser U.) Chem1 Virtual Textbook

