17.5: Precipitation Reactions

Introduction

Precipitation reactions

\[\underbrace{ Ag^+(aq) + Cl^-(aq) \leftrightharpoons AgCl(s)}_{\text{Precipitation of silver chloride}}\]

are the opposite of solubility expressions.

\[\underbrace{AgCl(s) \leftrightharpoons Ag^+(aq) + Cl^-(aq)}_{\text{Dissolution of silver chloride}} , \; \; K_{sp} =[Ag^+][Cl^-]\]

Therefore solubility constants can be used to determine if a precipitate will form. Although we could write these as precipitation reactions (in which case K_ppt = 1/K_sp ), we will use solubility expressions and state that a precipitate will form for a "Product Loaded System," (when reactants are formed), that is, when the back reaction occurs. Review section 15.2.5, the Reaction Quotient.

K_sp and Q

Q, the reaction quotient is the equilibrium constant expression at any condition, and a review of 15.2.5, shows there are three possibilities.

• Q=K, No reaction, system is at equilibrium
• Q>K, Product loaded, reactants are produced until Q=K
• Q<K, Reactant loaded, products are produced until Q=K

A precipitate forms if Q>K_sp .

Exercise \(\PageIndex{1}\)

The solubility product of calcium fluoride (CaF₂) is 3.45 × 10⁻¹¹. If 2.0 mL of a 0.10 M solution of NaF is added to 128 mL of a 2.0 × 10⁻⁵M solution of Ca(NO₃)₂, will CaF₂ precipitate?

Answer

\(Q=[Ca^{+2}][F^-]^2 \)

\[[Ca^{+2}]=\frac{n_{Ca^{+2}}}{V_T}=\frac{0.128L\left ( 2.0x10^{-5}M \right )}{0.128L+.002L}=1.97x10^{-5}M\]

\[[F^{-}]=\frac{n_{F^{-}}}{V_T}=\frac{0.002L\left ( 0.10M \right )}{0.128L+.002L}=1.54x10^{-3}M\]

\[Q=[1.97x10^{-5}][1.54x10^{-3}]^2=4.7x10^{-11}\]

Yes because Q>K_sp , but not much, as it is very close.

 

.

Fractional Precipitation 

Two dissolved ions can be separated out if they form salts of different solubilities with the same counter ion.  Consider the separation of Ag⁺(aq) from Pb⁺²(aq), both of which form insoluble salts with chloride

\[K_{sp}(PbCl_2) \; = \; 1.6x10^{-5} \\ K_{sp}(AgCl )\; = \; 1.8x10^{-10}\]

There are three possibilities

1. Both are Product loaded  (Q>K for both salts) and reactants are formed, making precipitates (remember, precipitates are the reactants not the products).

salt(s)  ->  cations(aq) + anions(aq)

\[AgCl(s) \leftrightharpoons Ag^+(aq)+Cl^-(aq) \\ PbCl_2(s) \leftrightharpoons Pb^{+2}(aq)+2Cl^-(aq) \]

2. Both are Reactant loaded (Q<K for both salts) and products are formed and both dissolve
3. One is product loaded (Q>K) and the other is reactant loaded (Q<K). The first forms a precipitate and the second dissolves.  

 

 

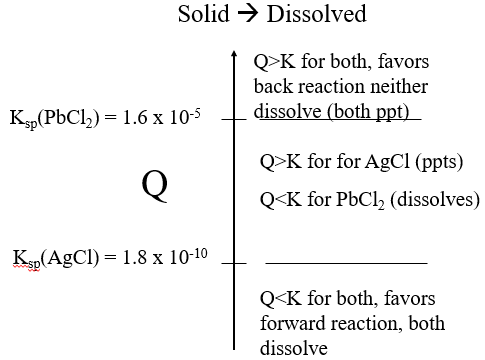
Figure \(\PageIndex{1}\): When Q>1.6x10^-5 both silver and lead(II) chloride precipitate.  When Q< 1.8x10^-10 they both dissolve, and if Q is between those values only the silver chloride precipitates . (Copyright; Bob Belford CC.0)

 

Example \(\PageIndex{1}\)

Consider a solution containing 0.1M silver nitrate and 0.1 M lead(II) nitrate that you wish to separate by adding chloride.  Over what range of chloride will one precipitate and the other not, and which one will precipitate.

\[K_{sp}(PbCl_2 \; = \; 1.6x10^{-5} \\ K_{sp}(AgCl \; = \; 1.8x10^{-10}\]

Solution

Step 1: Find the chloride concentration for each equilibria where Q=K

\[K_{PbCl_2}=[Pb^{+2}][Cl^-]^2 = 1.6x10^{-5}\;\;  \therefore \; \; [Cl^-]=\sqrt{\frac{K_{PbCl_2}}{[Pb^{+2}]}}=\sqrt{\frac{1.6x10^{-5}}{0.1}}=0.00158 \\ 
K_{AgCl}=[Ag^+][Cl^-]\;=\;1.8x10^{-10} \; \; \; \therefore \; \; \; [Cl^-]=\frac{K_{AgCl}}{[Ag^+]}=\frac{1.8x10^{-10}}{0.1}= 1.8x10^{-9}\]

Step 2: Find range where Q>K for only one reactant (anything above that they both precipitate) and for which Q<K for only one reactant (below which they both dissolve).  So if [Cl^-]> 0.00158 than Q is greater than both Ks and a precipitate forms, if  [Cl^-]< 1.8x10^-9 than Q is less that both Ks and they both dissolve, and for the range \[1.8x10^{-9} <[Cl^-]<0.00158\] only AgCl will precipitate

 

Contributors and Attributions

Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, [e-mail]. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to: