15.2: Equilibrium Constant and Reaction Quotient
- Page ID
- 60734
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
In this section we will mathematically describe the concentrations of products and reactants for a system that has reached equilibrium in terms of an Equilibrium constant. We use K (capital K) for the equilibrium constant and it is unitless, and we use small k for rate constants, and it has units.
\[\begin{align}aA+bB &\rightleftharpoons cC+dD \nonumber \\ \nonumber \\ K & =\dfrac{[C]^c[D]^d}{[A]^a[B]^b} \end{align}\]
Where a, b, c & d are the stoichiometric coefficients of the chemical species A,B,C & D respectively.
NOTE: K is unitless and we use [A] to represent the concentration of "A", but this is really a simplification, and equilibrium constants are calculated using “effective concentrations,” or activities, of reactants and products, which are the ratios of the measured concentrations to a standard state of 1 M. As shown in Equation 15.2.2, the units of concentration cancel, which makes \(K\) unitless as well:
\[ \dfrac{[A]_{measured}}{[A]_{standard\; state}}=\dfrac{[A]\cancel{M}}{[1]\cancel{M}} = [A]\dfrac{\cancel{\frac{mol}{L}}}{\cancel{\frac{mol}{L}}} =[A](unitless)\]
Equilbrium and Rate Constants
Capital K = Equilibrium constant and is unitless
Small k = Rate constant and has units
(which depend on overall order of reaction)
Equilibrium Constant and Kinetics
Consider the general equation
\[\large aA+bB \underset{k_{r}} {\overset{k_f} {\rightleftharpoons}} cC+dD \nonumber \]
At equilibrium, the rate of the foward reaction equals the rate of the reverse (or back reaction).
\[\begin{align} Rate_{forward} & = Rate_{reverse} \nonumber \\ \nonumber \\ k_{f}[A]^{m}[B]^{n} & = k_{r}[C]^{p}[D]^{q} \end{align}\]
Rearranging
\[K =\frac{k_{f}}{k_{r}} = \frac{[C]^p[D]^q}{[A]^m[B]^n} = \frac{[C]^c[D]^d}{[A]^a[B]^b} \label{15.2.4}\]
To understand why the stoichiometric coefficients are the exponents in the equilibrium constant while the rate law has experimentally determined orders of reaction, you need to take into account that the actual stoichiometric equation is the result of a series of coupled mechanistic equations, and for each elementary mechanistic step the order of reaction is the coefficient. This will be revisited later when equilibrium constants of coupled equations are covered, and right now this can be considered to be a consequence of the conservation of mass.
There is also a sleight of hand in Equation \ref{15.2.4}, in that small \(k\)'s have units and capital \(K\)'s do not, that is the rate is not really of the concentration, but the "effective concentration" or activity. In this class we will ignore this, and treat rate constants as having units, and equilibrium constants as not having units.
Magnitude of K
The magnitude of K tells you if you have a Products, Reactants or a mixture of products and reactants once a reaction is over and equilibrium is reached. The Rule of thumb is that products are favored for K>1000, reactants are favored if K<0.001 and a mixture if 0.001<K<1000.

Figure\(\PageIndex{1}\): Composition of equilibrium mixtures as a function of K
| Reaction | Temperature (K) | Equilibrium Constant (K) |
|---|---|---|
| *Equilibrium constants vary with temperature. The K values shown are for systems at the indicated temperatures. | ||
| \(S_{(s)}+O_{2(g)} \rightleftharpoons SO_{2(g)}\) | 300 | \(4.4 \times 10^{53}\) |
| \(2H_{2(g)}+O_{2(g)} \rightleftharpoons 2H_2O{(g)}\) | 500 | \(2.4 \times 10^{47}\) |
| \(H_{2(g)}+Cl_{2(g)} \rightleftharpoons 2HCl_{(g)}\) | 300 | \(1.6 \times 10^{33}\) |
| \(H_{2(g)}+Br_{2(g)} \rightleftharpoons 2HBr_{(g)}\) | 300 | \(4.1 \times 10^{18}\) |
| \(2NO_{(g)}+O_{2(g)} \rightleftharpoons 2NO_{2(g)}\) | 300 | \(4.2 \times 10^{13}\) |
| \(3H_{2(g)}+N_{2(g)} \rightleftharpoons 2NH_{3(g)}\) | 300 | \(2.7 \times 10^{8}\) |
| \(H_{2(g)}+D_{2(g)} \rightleftharpoons 2HD_{(g)}\) | 100 | \(1.92\) |
| \(H_{2(g)}+I_{2(g)} \rightleftharpoons 2HI_{(g)}\) | 300 | \(2.9 \times 10^{−1}\) |
| \(I_{2(g)} \rightleftharpoons 2I_{(g)}\) | 800 | \(4.6 \times10^{−7}\) |
| \(Br_{2(g)} \rightleftharpoons 2Br_{(g)}\) | 1000 | \(4.0 \times 10^{−7}\) |
| \(Cl_{2(g)} \rightleftharpoons 2Cl_{(g)}\) | 1000 | \(1.8 \times 10^{−9}\) |
| \(F_{2(g)} \rightleftharpoons 2F_{(g)}\) | 500 | \(7.4 \times 10^{−13}\) |
Notice in Table \(\PageIndex{1}\) that equilibrium constants decrease going down the table from very large numbers \(10^{53}\) to very small fractions, \(10^{-13}\). The reactions on the top essentially go to completion and are called "product favored reactions" because they favor the production of products at equilibrium, and the ones at the bottom are often called "reactant favored reactions", because as written, they favor reactants, and essentially do not make any products. Also note that the equilbrium constant is a function of temperature and thus the temperature is also given in the table.
Product Favored Reactions
K>>1: The reaction essentially goes to completion. These are essentially irreversible in the sense that reactants form products, but products do not form reactants.
Consider the simple reaction
\[aA \rightleftharpoons B \\ K =\frac{[B]^b}{[A]^a} \]
for K>>1
the numerator must be much greater than the denominator, so [B] > [A] at equilibrium.
Figure\(\PageIndex{2}\): The flat part of this curve shows when equilibrium is reached and the reaction is over and essentially all of the reactant (A) has converted to product (B). The above curve has a 1:1 ratio, and so the final [B] is roughly equal to the initial [A].
If the reaction in figure 15.2.2 was A \(\rightarrow\) 2B, the final B concentration would approach double the original A concentration.
Combustion of a hydrocarbon to carbon dioxide and water is a product favored reaction, and once the reaction is over all of the reactant will be converted to carbon dioxide and water.
Reactant Favored Reactions
K<<1 (a very small fraction), essentially nothing happens. These are essentially irreversible in the sense that products would form reactants, and reactants do nothing.
Consider the simple reaction
\[aA \rightleftharpoons B \\ K =\frac{[B]^b}{[A]^a} \]
for K<<1
the numerator must be much smaller than the denominator,
so [B] < [A] at equilibrium.
Figure\(\PageIndex{3}\): Shows that for a reactant favored reaction, essentially nothing happens. In general chemistry 1 you learned that silver chloride is an insoluble salt, and very little would dissolve if you added it to water. This would be reflected by it having a very small equilibrium constant. In fact, K for silver chloride dissolving in water is 1.8x10-10.
Reaction Mixtures
Reactions that result in a mixture of products and reactants have \(K\) around one, and as a rule of thumb we say if K is between and thousand and a thousandth, (1,000>K>1/1000), both reactants and products exist once the reaction is over.
Consider the gas phase formation of sulfur trioxide from sulfur dioxide and water which has a \(K\) near 1.
\[\large 2SO_{2} + O_{2}\rightleftharpoons 2SO_{3}\nonumber \]
In Figure\(\PageIndex{4}\), you have two kinetics plots for the above reaction. In (a) you start with O2 & SO2 with no SO3 and so the reaction must go in the forward direction and make SO3, which it does until you reach equilibrium (realize the flat part of each reaction curve means the change in concentration of that species is zero, so it is not being consumed or produced). In (b) you start with SO3 and no O2 or SO2 and so the back reaction must occur forming the "reactants" O2 and SO2.
Figure\(\PageIndex{4}\): Kinetics curves showing forward and back reactions for the following reaction \(2SO_{2} + O_{2}\rightleftharpoons2SO_{3}\), (a) is forward, (b) is backwards. Note in (b) that SO2 and O2 both start at zero concentration and that from the balanced equation, the rate of SO2 production is twice that of O2 and so at any point in time, the SO2 concentration is twice thed O2 concentration. Image used with permission (CC BY-3.0; OpenStax)
It should be noted that once equilibrium is reached, the equilibrium constant expression for the above two curves must equal, as expressed in Equation \ref{15.2.7}.
\[\left ( \frac{[SO_{3}]^{2}}{[O_{2}][SO_{2}]^{2}} \right )_{(a)}=\left ( \frac{[SO_{3}]^{2}}{[O_{2}][SO_{2}]^{2}} \right )_{(b)} \label{15.2.7}\]
Note, the above graph may be misleading, the above concentrations for each species do not need to be equal, but their values as expressed in the equilibrium constant expressions (Equation \ref{15.2.7}) do need to be equal.
Write the equilibrium constant for each reaction.
- \(N_{2(g)}+3H_{2(g)} \rightleftharpoons 2NH_{3(g)}\)
- \(CO_{(g)}+\frac{1}{2}O_{2(g)} \rightleftharpoons CO_{2(g)}\)
- \(2CO_{2(g)} \rightleftharpoons 2CO_{(g)}+O_{2(g)}\)
Given: balanced chemical equations
Asked for: equilibrium constant expressions
Strategy:
Refer to Equation 15.2.1. Place the arithmetic product of the concentrations of the products (raised to their stoichiometric coefficients) in the numerator and the product of the concentrations of the reactants (raised to their stoichiometric coefficients) in the denominator.
Solution:
The only product is ammonia, which has a coefficient of 2. For the reactants, \(N_2\) has a coefficient of 1 and \(\ce{H2}\) has a coefficient of 3. The equilibrium constant expression is as follows:
\[\dfrac{[NH_3]^2}{[N_2][H_2]^3}\]
The only product is carbon dioxide, which has a coefficient of 1. The reactants are \(CO\), with a coefficient of 1, and \(O_2\), with a coefficient of \(\frac{1}{2}\). Thus the equilibrium constant expression is as follows:
\[\dfrac{[CO_2]}{[CO][O_2]^{1/2}}\]
This reaction is the reverse of the reaction in part b, with all coefficients multiplied by 2 to remove the fractional coefficient for \(O_2\). The equilibrium constant expression is therefore the inverse of the expression in part b, with all exponents multiplied by 2
\[\dfrac{[CO]^2[O_2]}{[CO_2]^2}\]
Exercise \(\PageIndex{1}\)
Write the equilibrium constant expression for each reaction.
- \(N_2O_{(g)} \rightleftharpoons N_{2(g)}+\frac{1}{2}O_{2(g)}\)
- \(2C_8H_{18(g)}+25O_{2(g)} \rightleftharpoons 16CO_{2(g)}+18H_2O_{(g)}\)
- \(H_{2(g)}+I_{2(g)} \rightleftharpoons 2HI_{(g)}\)
- Answer a
-
\(K=\dfrac{[N_2][O_2]^{1/2}}{[N_2O]}\)
- Answer b
-
\(K=\dfrac{[CO_2]^{16}[H_2O]^{18}}{[C_8H_{18}]^2[O_2]^{25}}\)
- Answer c
-
\(K=\dfrac{[HI]^2}{[H_2][I_2]}\)
Example \(\PageIndex{2}\)
Predict which systems at equilibrium will (a) contain essentially only products, (b) contain essentially only reactants, and (c) contain appreciable amounts of both products and reactants.
- \(H_{2(g)}+I_{2(g)} \rightleftharpoons 2HI_{(g)}\;\;\; K_{(700K)}=54\)
- \(2CO_{2(g)} \rightleftharpoons 2CO_{(g)}+O_{2(g)}\;\;\; K_{(1200K)}=3.1 \times 10^{−18}\)
- \(PCl_{5(g)} \rightleftharpoons PCl_{3(g)}+Cl_{2(g)}\;\;\; K_{(613K)}=97\)
- \(2O_{3(g)} \rightleftharpoons 3O_{2(g)} \;\;\; K_{(298 K)}=5.9 \times 10^{55}\)
Given: systems and values of \(K\)
Asked for: composition of systems at equilibrium
Strategy:
Use the value of the equilibrium constant to determine whether the equilibrium mixture will contain essentially only products, essentially only reactants, or significant amounts of both.
Solution:
- Only system 4 has \(K \gg 10^3\), so at equilibrium it will consist of essentially only products.
- System 2 has \(K \ll 10^{−3}\), so the reactants have little tendency to form products under the conditions specified; thus, at equilibrium the system will contain essentially only reactants.
- Both systems 1 and 3 have equilibrium constants in the range \(10^3 \ge K \ge 10^{−3}\), indicating that the equilibrium mixtures will contain appreciable amounts of both products and reactants.
Exercise \(\PageIndex{2}\)
Hydrogen and nitrogen react to form ammonia according to the following balanced chemical equation:
\[3H_{2(g)}+N_{2(g)} \rightleftharpoons 2NH_{3(g)}\]
Values of the equilibrium constant at various temperatures were reported as
- \(K_{25°C} = 3.3 \times 10^8\),
- \(K_{177°C} = 2.6 \times 10^3\), and
- \(K_{327°C} = 4.1\).
- At which temperature would you expect to find the highest proportion of \(H_2\) and \(N_2\) in the equilibrium mixture?
- Assuming that the reaction rates are fast enough so that equilibrium is reached quickly, at what temperature would you design a commercial reactor to operate to maximize the yield of ammonia?
- Answer a
-
327°C, where \(K\) is smallest
- Answer b
-
25°C
K for Reverse Reactions
If you write a reaction backward K is the reciprocal
Forward Reaction
\[a[A] + b[B] \rightleftharpoons c[C] + d[D] \; \\ \; K_{forward}=\frac{[C]^c[D]^d}{[A]^a[B]^b}\]
Reaction written backwards
\[ c[C] + d[D] \rightleftharpoons a[A] + b[B] \; \\ \; K_{backward}=\frac{[A]^a[B]^b}{[C]^c[D]^d}\]
Therefore
\[K_{forward} = \frac{1}{K_{backward}}\]
Heterogeneous Equilibria
Solid and pure liquids (not solutions) have constant densities and therefore their concentrations are constant and do not change as a reaction proceeds and thus they are not kept in the equilibrium constant. In the following reaction the iron and iron (II) oxide have constant densities, which don't change as they get consumed or produced, and thus they can be omitted in the equilibrium calculations. Note, they need to be present, but their concentrations are always the same.
\[Fe(s) + CO_2(g) \rightleftharpoons FeO(s) + CO(g) \\ \; \\ K=\frac{[CO]}{[CO_2]} \]
Solubility of salts is a common heterogeneous equilibria and will be studied in depth in chapter 17.
Exercise \(\PageIndex{1}\)
Write the equilibrium constant expression for the solubility of lead(II) iodide.
- Answer
-
The reaction is \[PbI_2(s) \rightleftharpoons Pb^{+2}(aq) + 2I^- \\ \; \\ K=[Pb^{+2}][I^-]^2] \nonumber \]
Excess Reagents
If a chemical species involved in a reaction is in great excess compared to the other species, its concentration remains constant and so like solids and pure substances, its concentration does not effectively change. This typically happens when a reaction involves a solvent, such as in the case of aqueous acid base reactions involving the protonation or deprotonation of water.
\[HA(aq)+H_2O(l)⇌H_3O^+(aq)+A^-(aq)\]
At first glance this gives an equilibrium constant of
\[K=\frac{[H_{3}O^{+}][A^{-}]}{[HA][H_{2}O]}\]
But lets look at a dilute solution at say pH = 2, where [H3O+] = 10-pH = 0.01M and [H2O] = 55.56M
\[[H_2O]=\frac{1000g\;H_2O}{L} \left ( \frac{mol H_2O}{18g} \right )=55.5\bar{5}M\]
and so the water concentration is of the order of 10,000 more concentrated the the acid, and its concentration essentially stays constant. This results in an acid dissociation constant where the water is absorbed into Ka ( a constant divided by a constant is a constant) and we will cover this in great detail in chapter 16.
\[K_a= \frac{K}{[H_2O]}=\frac{[H_{3}O^{+}][A^{-}]}{[HA]}\]
So if one reagent is of orders magnitude greater than the others, as if often the case when a solvent is involved in a reaction, its concentration is effectively constant and you can remove it from the equilibrium constant
Gas Phase Equilibria
For the generic equation, \[aA + bB \rightleftharpoons cC + dD\]
The equilibrium constant for a gas is Kp:
\[K_p = \dfrac{P_C^c P_D^d}{P_A^aP_B^b}\]
This can be related to the concentration based equilibrium constant, \(K_c\).
\[K_c = \dfrac{[C]^c[D]^d}{[A]^a[B]^b} \label{15.2.10}\]
By the relationship
\[K_{p}=K_{c}(RT)^{\Delta n} \\ \text{where,} \\ \Delta n=\sum \text{Product Stoichiometric Coef }-\sum \text{Reactant Stoichiometric Coef} \label{15.2.11}\]
Note, Equation \ref{15.2.11} can be derived from the Ideal gas equation of state
\[P_{A}V=n_{A}RT \\ \therefore \\ [A]=\frac{n_{A}}{V}=\frac{P_{A}}{RT} \label{15.2.12}\]
In video 15.2.1, Equation \ref{15.2.11} is derived by substituting Equation \ref{15.2.12} into Equation \ref{15.2.10}.
Video\(\PageIndex{1}\): 5.06 min YouTube showing derivation of eq. 15.2.15
Example \(\PageIndex{3}\): The Haber Process for making ammonia
The equilibrium constant for the reaction of nitrogen and hydrogen to give ammonia is 0.118 at 745 K. The balanced equilibrium equation is as follows:
\[N_{2(g)}+3H_{2(g)} \rightleftharpoons 2NH_{3(g)}\]
What is \(K_p\) for this reaction at the same temperature?
Given: equilibrium equation, equilibrium constant, and temperature
Asked for: \(K_p\)
Strategy:
Use the coefficients in the balanced chemical equation to calculate \(Δn\). Then use Equation \(\ref{Eq18}\) to calculate \(K\) from \(K_p\).
Solution:
This reaction has 2 mol of gaseous product and 4 mol of gaseous reactants, so \(\Delta{n} = (2 − 4) = −2\). We know \(K\), and \(T = 745\; K\). Thus, from Equation \(\ref{Eq15}\), we have the following:
\[ \begin{align*} K_p &=K(RT)^{−2} \\[5pt] &=\dfrac{K}{(RT)^2} \\[5pt] &=\dfrac{0.118}{\{ [0.08206(L \cdot atm)/(mol \cdot K)][745\; K]\}^2} \\[5pt] &=3.16 \times 10^{−5} \end{align*}\]
Because \(K_p\) is a unitless quantity, the answer is \( K_p = 3.16 \times 10^{−5}\).
Exercise \(\PageIndex{3}\)
Calculate \(K_p\) for the reaction
\[\ce{2SO2(g) + O2(g) \rightleftharpoons 2SO3(g)} \nonumber\]
at 527°C, if \(K = 7.9 \times 10^4\) at this temperature.
- Answer
-
\(K_p = 1.2 \times 10^3\)
Note: A deeper dive
The above derivation works and is taught in most freshmen chemistry courses, but note, as derived, the \(K_p\) would have units of (RT)\(^{\Delta n}\). Just as the concentration is really a relative concentration (activity), we need to realize the pressure terms are also relative, and a more formal approach would be to treat the pressure as
\[P_{A}^{a}=\left ( \frac{P_{A}}{P^{0}} \right )^{0}, \text{where} P^{a} \text{is the standard pressure (1 bar=0.987 atm)}\]
Lets look at \[aA\rightleftharpoons bB\]
now
\[\begin{align} \large{K_{P}} & \large{=\frac{\left (\frac{P_{B}}{P^{0}} \right )^{b}}{\left (\frac{P_{A}}{P^{0}} \right )^{a}}} \nonumber \\ \nonumber \\ \text{which is unitless,} & \text{ noting for gas Z} \nonumber \\ \nonumber \\ P_{Z} =\frac{n_{Z}}{V}RT & =[Z]RT(atm) \nonumber \\ \nonumber \\ \text{substituting for} \; & P_{A} \; and \; P_{B} \; gives \nonumber \\ \nonumber \\ \large{K_{P}} & =\large{\frac{\left (\frac{[B]RT\textcolor{\red}{\cancel{(atm)}}}{P^{0}(\textcolor{red}{\cancel{atm}})} \right )^{b}}{\left (\frac{[A]RT\textcolor{red}{\cancel{(atm)}}}{P^{0}(\textcolor{red}{\cancel{atm}})} \right )^{a}}} \\ \nonumber \\ & =\frac{[B]^{b}}{[A]^a}\left ( \frac{(RT)^{b}}{(RT)^{a}} \right )\left ( \frac{(P^{0})^{a}}{(P^{0})^{b}} \right ) \nonumber \\ noting \; P^{0} = \text{1 atm, so last term of above eq. is 1} \nonumber \\ \nonumber \\ K_{P} & =K_{C}(RT)^{b-a}, or \nonumber \\ K_{P} & =K_{C}(RT)^{\Delta n} \; where \nonumber \\ \Delta n & = b-a \text{(products minus reactants)} \end{align} \nonumber \]
Equation 15.2.15 of above derivation shows why the eq \(K_{p}=K_{c}(RT)^{\Delta n}\) has no units, even though it looks like RT has units (they canceled out in step 15.2.15).
Note the following problem involves three phases
Exercise \(\PageIndex{1}\)
Write the equilbrium constant expression for the following reaction
\[Mg(s) + 2HCl(aq) \rightleftharpoons MgCl_2(aq) + H_2(g)\]
- Answer
-
\[K= \frac{[MgCl_2][P_{H_2}]}{[HCl]^2} \]
Reaction Quotient
The reaction quotient (Q) describes the state of a system with respect to equilibrium, and tells you if a chemical reaction will proceed, and if so, in what direction. Mathematically, it is the equlibrium constant expression, but using the concentrations of any system, whether it is at equilibrium, or not. For a chemical reaction to occur, Q \(\neq\) K. There are three possiblities.
- Q=K, No reaction, system is at equilbrium
- Q>K, Product loaded, reactants are produced until Q=K
- Q<K, Reactant loaded, products are produced until Q=K
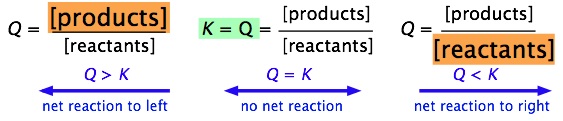
Product Loaded Systems
For a product loaded system, Q>K.
What does this mean? It means the reaction will not proceed as written, in fact the opposite will happen, and you will make reactants.
The concept is simple, and you have "loaded" your system with products it will make reactants. That is, what you call reactants (the species on the left hand side of the equation) are not reactants, but products, and you make them.
Reactant Loaded Systems
For a reactant loaded system, Q<K.
What does this mean? It means the reaction will proceed as written, and reactants will form products.
Reaction Quotient Calculations
Catalysts
Catalysts do not change the value of the equilibrium constant, they speed up the rate at which a reaction reaches equilibrium. That is, they speed up both the forward and the reverse reactions. Lets go back to eq. 15.2.4, where kFor is the forward rate constant, and kRev is the reverse rate constant. General chemistry students need to know that catalysts do not effect the equilibrium constant, but they do not need to derive this equation.
\[K =\frac{k_{For}}{k_{Rev}} =\frac{Ae^{-\frac{E_{a,For}}{RT}}}{Ae^{-\frac{E_{a,Rev}}{RT}}}=e^{\frac{E_{a,Rev}-E_{a,For}}{RT}}\]
We know that catalysts change the rate constant by lowering the activation energy. Lets say D is the amount the activation energy is lowered, so the catalyzed activation energy, Ea-CAT = Ea -D, and:
\[E_{a-CAT,For}= E_{a,For}-D \;\; and \;\; E_{a-CAT,Rev}= E_{a,Rev}-D\]
substituting for Kcat:
\[K_{CAT}=e^{\frac{E_{a-CAT,Rev}-E_{a-CAT,For}}{RT}}= e^{\frac{E_{a,Rev}-D-(E_{a,For}-D)}{RT}}=e^{\frac{E_{a,Rev}-E_{a,For}}{RT}}=K\]
Worksheets:
Equilibrium Constant Worksheet 1:
Equilibrium Constant Worksheet 1 Key:
Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:


