17.6: Equilibria Involving Complex Ions

Last updated
Save as PDF

Page ID: 60766

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Introduction

Metal cations can function as Lewis acids (review section 16.7.2.3) and form what are called coordination complexes. This is a type of Lewis acid/base reaction where the metal is the Lewis acid and the electron donor (lewis base) is called a ligand. Coordination complexes may be neutral or charged and if it is charged it is called a complex ion.

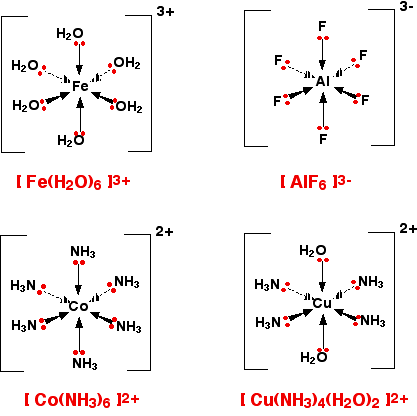
Figure 17.6.1 shows several complex ions and the formation of complexes can complicate other equilibria and influence the solubility of salts.

Video \(\PageIndex{1}\): Youtube video by Chemistry Channel visualizing how complex ions are formed (https://youtu.be/eLO0orGka8c)

Formation Constants

The following is a table of formation constants. An updated table (table E4) can always be found on LibreText by using the link at the header of each page, Reference Tales/Equilibrium Constants/E4: Complex Ion Formation Constants

Formation Constants for Complex Ions
Equilibrium	K_f
\(\ce{Al^3+ + 6F- ⇌ [AlF6]^3-}\)	7 × 10¹⁹
\(\ce{Cd^2+ + 4NH3 ⇌ [Cd(NH3)4]^2+}\)	1.3 × 10⁷
\(\ce{Cd^2+ + 4CN- ⇌ [Cd(CN)4]^2-}\)	3 × 10¹⁸
\(\ce{Co^2+ + 6NH3 ⇌ [Co(NH3)6]^2+}\)	1.3 × 10⁵
\(\ce{Co^3+ + 6NH3 ⇌ [Co(NH3)6]^3+}\)	2.3 × 10³³
\(\ce{Cu+ + 2CN ⇌ [Cu(CN)2]-}\)	1.0 × 10¹⁶
\(\ce{Cu^2+ + 4NH3⇌[Cu(NH3)4]^2+}\)	1.7 × 10¹³
\(\ce{Fe^2+ + 6CN- ⇌[Fe(CN)6]^4-}\)	1.5 × 10³⁵
\(\ce{Fe^3+ + 6CN- ⇌[Fe(CN)6]^3-}\)	2 × 10⁴³
\(\ce{Fe^3+ + 6SCN- ⇌[Fe(SCN)6]^3-}\)	3.2 × 10³
\(\ce{Hg^2+ + 4Cl- ⇌[HgCl4]^2-}\)	1.1 × 10¹⁶
\(\ce{Ni^2+ + 6NH3⇌[Ni(NH3)6]^2+}\)	2.0 × 10⁸
\(\ce{Ag+ + 2Cl- ⇌[AgCl2]-}\)	1.8 × 10⁵
\(\ce{Ag+ + 2CN- ⇌[Ag(CN)2]-}\)	1 × 10²¹
\(\ce{Ag+ + 2NH3⇌[Ag(NH3)2]+}\)	1.7 × 10⁷
\(\ce{Zn^2+ + 4CN- ⇌[Zn(CN)4]^2-}\)	2.1 × 10¹⁹
\(\ce{Zn^2+ + 4OH- ⇌[Zn(OH)4]^2-}\)	2 × 10¹⁵
\(\ce{Fe^3+ + SCN- ⇌[Fe(SCN)]^2+}\)	8.9 × 10²
\(\ce{Ag+ + 4SCN- ⇌[Ag(SCN)4]^3-}\)	1.2 × 10¹⁰
\(\ce{Pb^2+ + 4I- ⇌[PbI4]^2-}\)	3.0 × 10⁴
\(\ce{Pt^2+ + 4Cl- ⇌[PtCl4]^2-}\)	1 × 10¹⁶
\(\ce{Cu^2+ + 4CN⇌[Cu(CN)4]^2-}\)	1.0 × 10²⁵
\(\ce{Co^2+ + 4SCN- ⇌[Co(SCN)4]^2-}\)	1 × 10³

Complex Ion Formation

This section is under construction

Consider the formation of the complex ion [Cu(CN)₄]^-2(aq),

Cu⁺²(aq) + 4CN^-(aq) \(\leftrightharpoons\) [Cu(CN)₄]^-2(aq)

\(K_f=\frac{[Cu(CN)_4]^{-2}}{[Cu^{+2}][CN^{-}]^4} \) K_f=1.0x10²⁵.

What is the copper(II) ion concentration for 0.10M Cu(NO₃)₂?

Exercise \(\PageIndex{1}\)

What is the copper(II) ion concentration for 0.10M Cu(NO₃)₂?

Answer: Since it is a soluble nitrate salt it all dissociates, and the concentration is 0.10M.

Exercise \(\PageIndex{2}\)

What is the copper(II) ion concentration for 0.10M Cu(NO₃)₂if you add 1 mol of sodium cyanide to a liter of the 0.10M copper(II)nitrate solution? (K_f for [Cu(CN)₄]^-2(aq) = 1.0x10²⁵)

Answer

Since K_f=1x10^{25} >>1000 (very large) you assume the following equation goes to the right and all the cyanide becomes complexes

\[Cu^{+2}(aq) + 4CN^- (aq)\leftrightharpoons [Cu(CN)_4]^{-2} \nonumber\]

\[Cu(CN)_4^{-2}(aq) = \frac{CN^-}{4} =\frac{1}{4}=0.25M = f\nonumber\]

K_f=1x10²⁵, which is very very large, so assume almost all the copper is converted to the complex, also note,

\[K_{f}=\frac{\left [ Cu(CN)_{4}^{2+} \right ]}{\left [ Cu^{2+} \right ]\left [CN^-] \right ]^{4}}\nonumber\]

\[\left [ Cu^{2+} \right ]=\frac{ [ Cu(CN)_{4}^{2+} ]}{K_{f}[CN^-]^{4}}\nonumber\]

\[\left [ Cu^{2+} \right ]=\frac{\left [ 0.25 \right ]}{1*10^{25} [ 0.10 ]^{4}}=1.2*10^{-8}\nonumber\]

so \( [Cu[CN]₄]^{-2}=\frac{CN^-}{4}=0.25M \)

and what is it if you add 1 mol of sodium cyanide to a liter of the 0.10M copper(II)nitrate solution? (K_f for [Cu[CN)₄]^-2(aq) = 1.0x10²⁵)

Contributors and Attributions

Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to: