14.6: Energetics and Reaction Rates
- Page ID
- 60729
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
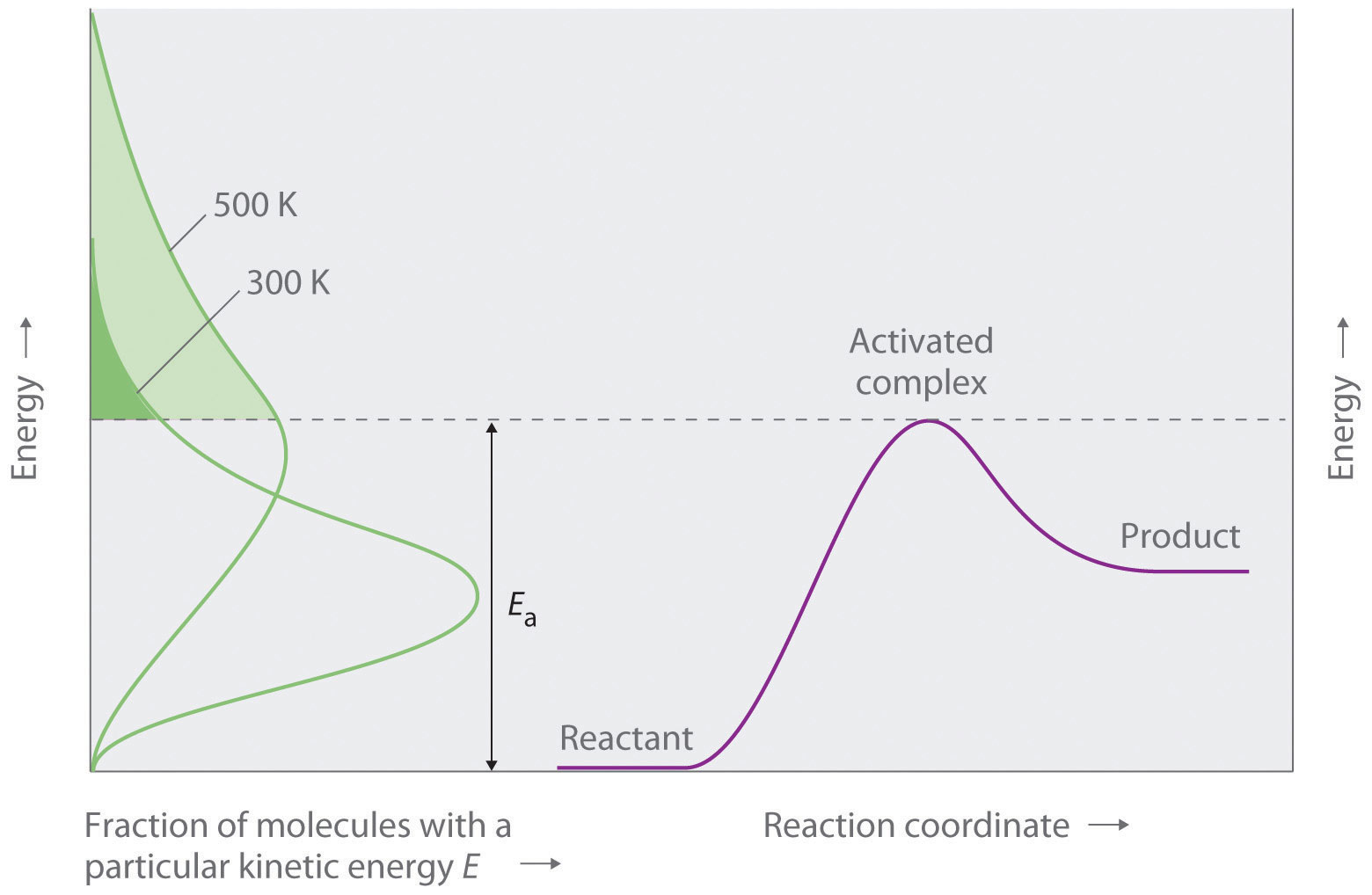
In this section we will look at the temperature dependence of the rate law, and the effect of catalysts. Lets start with a simple energetic perspective. We know that the energy change of a reaction can be endothermic or exothermic. We know that enthalpy and internal energy are state functions, and the energy difference between the two state is independent of the path, that is, how the atoms rearranged and what intermediates were formed as they transformed from reactants to products. But there was an actual path, or mechanism by which the connectivity of the atoms of the reactants rearranged to produce the products. What we now want to do is look at the actual path that atoms took, and what we discover is that the rate of reaction is a function of the path, or mechanism. That is, the energy difference is independent of the path, but the rate does depend on the path. Figure 14.5.1 is an energy plot for a reaction as reactants become products that we commonly call an Arrhenius diagram.
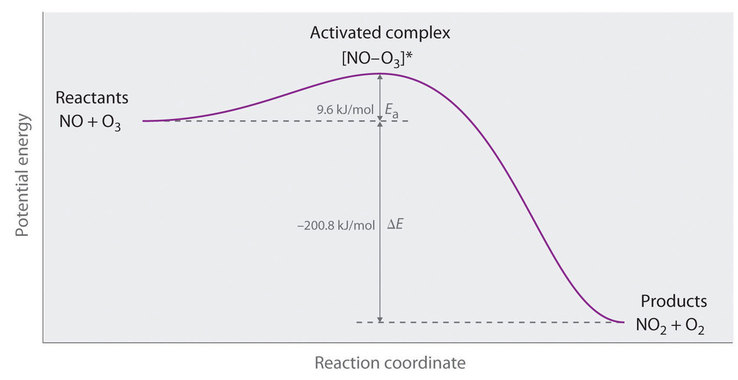
Figure \(\PageIndex{1}\) is a very important diagram to understand, and it is also a major simplification of what is really happening, but it is very useful. We know from the first law of thermodynamics that energy is conserved and that the energy difference between the final state (products) and the initial state (reactants) is independent of the path. It is also intuitive that energy is added to start breaking bonds (or intermolecular forces) and so a reaction starts with an endothermic step, which will be followed by an exothermic step as products are formed. But what were the states in between? The truth is, reactions can simultaneously proceed along many paths, and in the Arrhenius diagram we have simplified this to just one path, the lowest energy path, which we shall call the reaction coordinate. That is, in reality reactions involve many molecules and they do not all use the same path, but most use the path of lowest energy, which is the one described in the Arrhenius diagram.
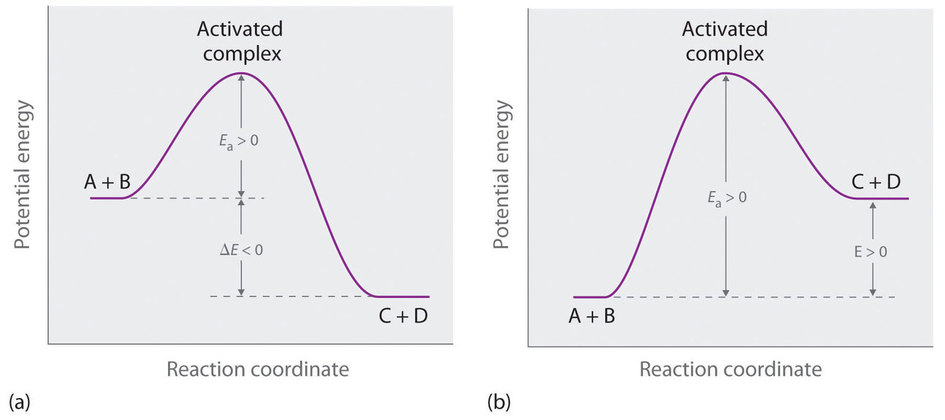
This process involves an activated complex, also called the transition state, which is not a stable molecule that you can put in a jar, but a transient structure that exists as atoms rearrange during the transition from reactants to products. In figure \(\PageIndex{2}\) the transition state shows a 5 bonded carbon which is clearly not a real molecule, but representative of this sort of transient pseudo-molecule that exists between reactants and products, as the reaction proceeds from reactants to products.
It may be worth taking a moment to reflect on what are reactants and products. That is, although they are different chemical species, the atoms are the same atoms, it is just the connectivity of their bonds that changes, but the atoms do not change.
Note, if the energy of activation of an exothermic reaction is less than the energy of reaction, the reaction is self perpetuating. This is the case in figure \(\PageIndex{1}\), where the energy released (-200.8kJ/mol) by some molecules as they react provides the Ea (9.6kJ/mol) others need to react. This is why a piece of paper is stable until it is ignited, when the energy relesed in combustion causes more paper molecules to ignite until it as turned to ashes. The following YouTube video does a good job of describing Arrhenius plots.
Rate Constant and Arrhenius Equation
The rate law for a reaction between two substances, A and B, is the following:
\[\text{rate}=k[A]^m[B]^n\]
Actually, the rate constant is not a constant, but a function of temperature, which is mathematically described by the Arrhenius equation, where R has units of 8.314J/mol-K
\[\large k=Ae^{-\frac{E_{a}}{RT}}\]
Note that the rate constant has two components, the pre-exponential "A" and the exponential \(e^{-\frac{E_{a}}{RT}}\). So the rate law also has a temperature component, which shows up when the Arrhenius equation is substituted for the rate constant in the rate law.
\[\text{rate}=Ae^{-\frac{E_{a}}{RT}}[A]^m[B]^n\]
Note, in the above equation, A is the pre-exponential of the Arrhenius equation and [A] is the concentration of reactant A.
Since this is an exponential equation, there are two ways of expressing it.
\[ k=Ae^{-\frac{E_{a}}{RT}}\] and \[ln k = ln A - \frac{E_a}{RT} \]
which is usually written in the form of a straight line
\[\ln k =- \dfrac{E_a}{R}\left ( \dfrac{1}{T} \right ) + \ln A \]
where ln k is a linear function of the reciprocal temperature \(\dfrac{1}{T}\).
You would use the exponential form if you are solving for k or "A", and the ln form if you are solving for Ea or T.
Pre-exponential
The pre-exponential "A" is a function of two factors, the frequency factor (z) and the steric factor (\(\rho\))
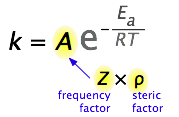
The pre-exponential "A" defines the largest possible value of the rate constant, assuming all collisions have enough energy to overcome the activation barrier. For reactions that involve two or more molecules interacting there are two factors involved in the pre-exponential, the frequency factor and the steric factor.
- The frequency factor determines the maximum rate of collisions, is a function of particle size, concentration and the rate of diffusion.
- The steric factor accounts for orientation, in that not all collisions have the correct orientation to result in a reaction, (see video \(\PageIndex{2}\)). The rule of thumb is that the more symmetric a molecule the larger the steric factor (a value of 1 means there is no effect, and the pre-exponential is determined by the collision frequency) and the more complicated a molecule, the smaller the steric factor (which is less than one), because only a fraction of the collisions have the correct orientation.
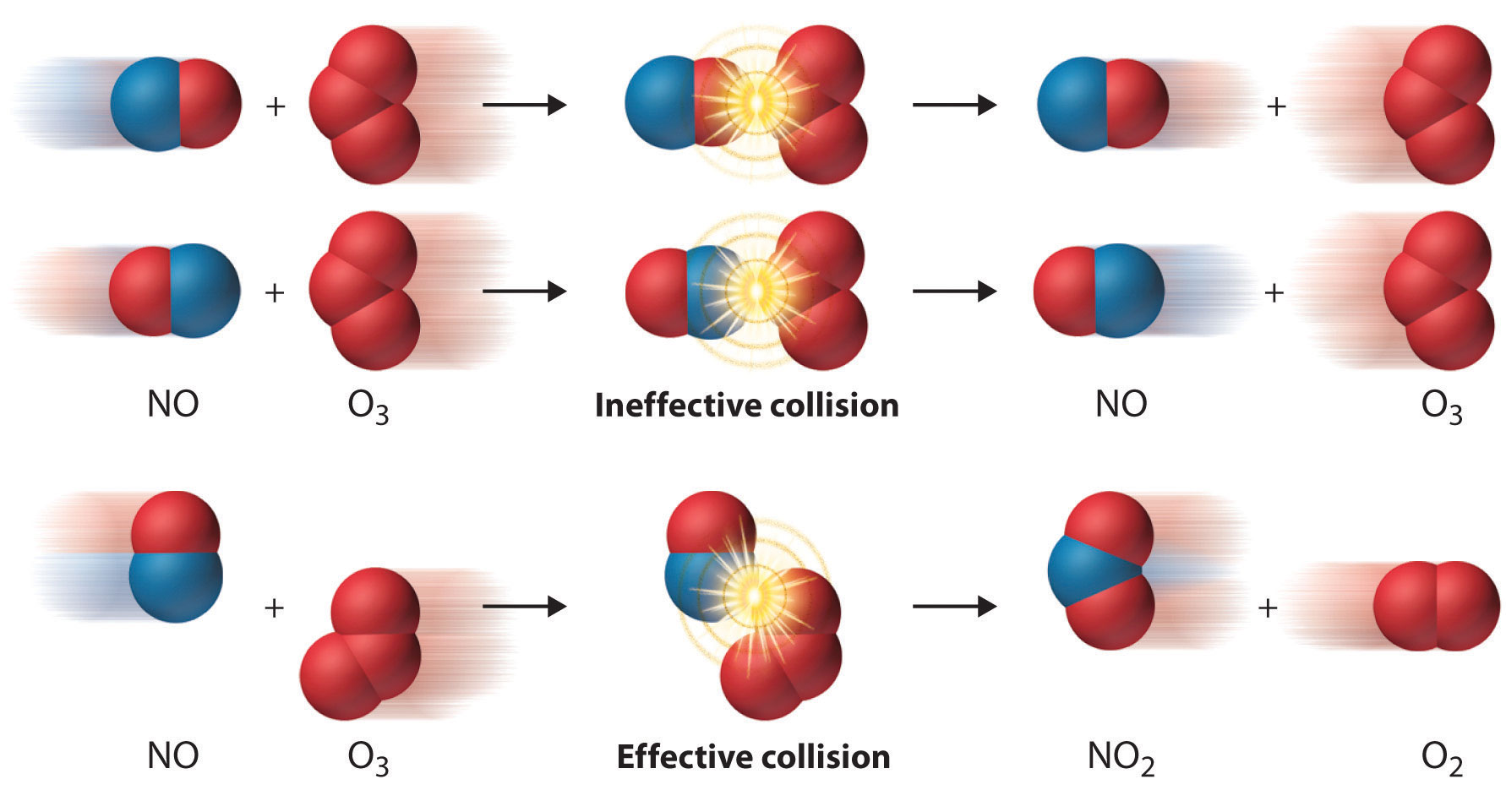
The following YouTube animation also shows the orientational dependence.
Exponential
Even if a collision is of the correct orientation it must also have enough energy to overcome the activation barrier, and the fraction of molecules with enough energy is described by the exponential of the arrhenius equation: The second term ( \(e^{-\frac{E_{a}}{RT}}\)) has a value between 0 and 1 and accounts for the fraction of molecules that have enough energy to overcome the activation barrier.
\[ \large e^{-\frac{E_a}{RT}}=\frac{1}{e^{\frac{E_a}{RT}}}\]
R=8.314J/mol-K, and that Energies of activation are often recorded in kJ/mol, and so care must be taken in calculations to convert these to the same value. Since Ea is positive (the energy of activation is endothermic, the energy added to the system to reach the transition state) and K is positive (absolute zero is the coldest temperature possible), the value of \(e^{-(E_a/RT)}\) is between 0 and 1
- At extreme high T or Low Ea: \(e^{-(E_a/RT)}\) approaches e0 = 1
- At extreme low T or High Ea: \(e^{-(E_a/RT)}\) approaches e-\(\infty\) = 0
Figure 14.5.5 provides a visualization on how this represents the fraction of collisions with enough energy to overcome the activation barrier. The y-axis represents the energy, and the horizontal line Ea represents the energy of activation. The green curves are the energy distribution profiles for a system of particles (say a mol) and at high T (500K) there are more molecules with higher kinetic energy than at low T (300K), and the fraction is the quantity above Ea divided by the entire area under the curve.
Arrhenius Eq. Calculations
Calculate the energy of activation if raising the temperature from 30oC to 40oC doubles the rate when all concentrations are maintained constant. You may want to review the material on the Clausius-Claperyon equation in chapter 11 (sec. 11.6.3) describing the vapor pressure above a liquid, as these equations model similiar processes.
Catalysts
Catalysts speed up the rate of reaction by changing the mechanism by which the reaction occurs. They are involved in multistep processes where they are consumed like a reactant in an early step to create an intermediate, and then are regenerated as a product in a subsequent step. The net effect is that the catalyst is regenerated after it is consumed, and thus can be used over and over. Catalysts also speed up the rate by lowering the activation energy. To indicate the presence of a catalyst they are written over the arrow as in equation 14.5.5, which describes the catalyzed production of B from A, where "Catalyst" is the identity of the catalyst
\[A\overset{Catalyst}{\rightarrow}B\]
Catalysts:
- Speed up the Rate of Reaction
- Change the mechanism of reaction
- Are not consumed by net reaction
- Consumed in early steps as intermediate species are formed
- Regenerated in later steps as intermediate species react
- Lower the Energy of Activation by forming intermediates with lower activation energy
All catalytic processes require the formation of one or more intermediates, which through subsequent steps reproduce the catalyst. Lets look at the simplest possible process, a two step reaction involving a single intermediate (A-CAT), where species A and B react to form C in the presence of a catalyst, CAT
\[A+B\overset{CAT}{\rightarrow}C\]
This can occur in a two step process where an intermediate A-CAT is formed.
\[\begin{align}\underbrace{A}_{reactant}+\underbrace{CAT}_{catalyst} & \rightarrow \underbrace{\text{A-CAT}}_{intermediate} \\ \underbrace{\text{A-CAT}}_{intermediate}+\underbrace{B}_{reactant} & \rightarrow \underbrace{C}_{product} +\underbrace{CAT}_{catalyst} \end{align}\]
When you add the above two equations you get the net reaction
\[A+B \rightarrow C\]
NOTE that in the coupled equations neither the catalyst or the intermediate show up in the net equation
- Catalyst: Consumed in Early Step and Produced in Later Step
- Intermediate: Produced in Early Step and Consumed in Later Step
Catalysts and the Arrhenius Equation
Figure \(\PageIndex{6}\) shows an Arrhenius diagram for both a catalyzed reaction (in blue) and a noncatalyzed reactions (in red). What is important to note is that the catalyzed path shows the formation of an intermediate. This is a real molecule and the deeper its well the more stable it is. Since forming the intermediate has a lower activation than the uncatalyzed path, the fraction of collisions with enough energy to overcome the activation barrier is higher, and so the rate is higher.
Lets revisit the Arrhenius Eq (14.5.2)
\[\large k=Ae^{-\frac{E_{a}}{RT}} \nonumber \]
We see there are two ways to increase the fraction of molecules that have enough energy to overcome the activation barrier \(e^{-\frac{E_{a}}{RT}}\), by raising the temperature or by lowering the activation energy, which is what a catalyst does. What needs to be understood is that in a real system, there are often competing reactions that can occur, and raising the temperature increases the rate of all of them, indiscriminately. While a catalyst can be very selective, and lower the activation energy of a specific reaction and thus allow you to increase the rate of a specific process, without increasing the rate of other processes.
It should also be noted that in real reactions there can be many intermediates, as illustrated by the Arrhenius diagram in figure 14.5.7
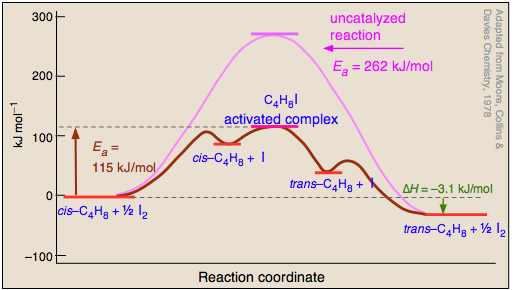
Another advantage of catalysts is that since they are regenerated, they quantity of reagents are decreased, and this fits in with one of the paradigms for green chemistry, which seeks to develop chemical chemical processes that use minimal resources and generate minimal waste.
Two basic types of catalysts
- Homogenous Catalysts
- Same phase as reactants
- Typically have a concentration dependence in the rate law
- Heterogeneous Catalysts
- Different phase than reactants
- efficiency influenced by surface area between phases.
Homogenous Catalysts
Oxides of nitrogen are byproducts of combustion and are produced by high flying aircraft in the upper atmosphere. The catalytic depletion of Ozone by Nitric Oxide (NO) in the stratosphere can have profound environmental effects because each NO molecule can destroys multiple ozone molecules.
The equation below describes the catalytic destruction of ozone by nitric oxide (NO). Note that NO is the catalyst and NO2 is the intermediate
\[\begin{align} NO + O_{3} & \rightarrow NO_{2} + O_{2} \nonumber\\ NO_{2} + O & \rightarrow NO + O_{2} \end{align}\]
Note that NO is the catalyst and NO2 is the intermediate, and that the net equation is
\[O_{3} + O \overset{NO}{\rightarrow } 2O_{2}\]
Homgenous catalysts are included in the concentration dependence of the rate law
\[R=k[O_3]^m[O]^n[NO]^p\]
Exercise \(\PageIndex{1}\)
Write the follow rate law for the decomposition of hydrogen peroxide by the homogenous catalysts bromine
\[2H_2O_2 \overset{Br_2}{\rightarrow} 2H_2O + O_2 \nonumber\]
- Answer
-
\[R=k[Br_2]^m(H_2O_2]^n \nonumber\]
Note that in a homogenous system, the catalyst concentration affects the rate of reaction, and so it is in the reaction law expression, like any other reactant. But it is a catalyts, because it is regenerated in a subsequent step.
Heterogeneous Catalysts
Heterogeneous catalyst involve more than one phase, and so the surface area between the phases influences the rate. Typical heterogeneous catalysts are solids that react with reactants that are in the liquid of gaseous phase, and since the catalyst is a solid, its concentration is constant and it does not appear in the rate equation.
The nickel catalyzed hydrogenation of ethylene (H2C=CH2) to ethane (H3CCH3) is an example of a heterogeneous catalyst,
Note, ethylene is stable in the presence of hydrogen and this makes sense, as there is no way the small diatomic hydrogen can approach both carbons in a single collision, split apart and form a bond with each. But by adsorbing into the catalytic surface they can then split apart and approach the carbons. It should be noted that the process of a gas reacting with a solid catalyst can be viewed to take place in three generic process, although as the video above shows, step 2, the actual reaction can be viewed to take place in multiple steps. But all heterogeneous catalysts must undergo the following 3 processes.
Process 1: Adsorption - reactants adsorb onto surface of heterogeneous catalyst
Process 2: Reactants interact and form products (which can involve multiple steps)
Process 3: Desorption - products leave catalytic surface, rejuvenating the catalyst so it can repeat the process and adsorb more reactants.
Poisoning a Catalyst occurs when a compound irreversibly adsorbs onto the surface and thus reduces the amount of active surface area. Many catalysts have active sites, which are specific regions of a molecule that has catalytic action. Enzymes are biological catalysts, most of which are made of proteins.
Enzymes
Enzymes are biological protein based catalysts. The following video shows an enzyme catalyzed reaction. Although many of the details in this video are advanced for this class, it gives you a good feel for the specificity of catalysts, and how catalytic reactions can involve multiple steps.
Test Yourself
Homework: Section 14.5
WorkSheets and Keys:
Query \(\PageIndex{1}\)
Query \(\PageIndex{2}\)
Query \(\PageIndex{3}\)
Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:
- Liliane Poirot


