14.7: Reaction Mechanisms
- Page ID
- 60730
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
Reaction Mechanism describe how a reaction actually proceeds, that is, what molecules colloid or spontaneously react. Most reactions are multistep, consisting of a series of coupled elementary reactions or steps, with each step typically involving one or two reactants.
An elementary reaction is a single step reaction involving 1 species decaying, or 2 or 3 molecules simultaneously colliding.
Molecularity
For an elementary step, the molecularly describes the number of particles involved in that step, and the order of reaction for each species is the stoichiometric coeficient of that species in the actual elementary step. The molecularity is the number of species involved with an elementary reaction. Molecularity can be described as unimolecular, bimolecular, or termolecular. Termolecular reactions are very rare as they require 3 particles colloiding with the correct orientation at the exact same time. Most reactions are unimolecular or bimolecular.
Unimolecular Elementary Reactions
These involve one species that spontaneously reacts, like the radioactive decay of an unstable radioisotope. The rate is proportional to the concentration
\[\begin{align} A & \rightarrow Products \nonumber \\ R & =k[A] \end{align}\]
That is, the coeficient of a unimolecular elementary reaction is its coeficient, and if we integrated the above equation we would have an exponential decay.
Bimolecular Elementary Reactions
A bimolecular collision requires two chemicals to colloid and from collision theory the rate is proportional to the concentration of each colliding chemical with an overall order of reaction equal to two. That is, if the colliding molecules are the same species, the order of reaction is 2 for that species.
\[\begin{align} 2A & \rightarrow Products \nonumber \\ R & =k[A]^{2} \end{align}\]
\[\begin{align} A + B & \rightarrow Products \nonumber \\ R & =k[A][B] \end{align}\]
Termolecular Elementary Reactions
A termolecular elementary reaction requires 3 species to colloid at the same time with the proper orientation and energy, and is thus very rare. But they can occur, especially under conditions of high pressure and high temperature where there is a high collision frequency and a lot of energy in collisions. From collision theory the overall molecularity is three, with the order of reaction for each species being the number of colliding particles of that species in the termolecular collision.
\[\begin{align} 3A & \rightarrow Products \nonumber \\ R & =k[A]^{3} \end{align}\]
\[\begin{align} 2A + B & \rightarrow Products \nonumber \\ R & =k[A]^{2}[B] \end{align}\]
\[\begin{align} A + B + C & \rightarrow Products \nonumber \\ R & =k[A][B][C] \end{align}\]
Higher order reactions do not occur, and it should be emphasized the termolecular elementary reactions are rare. Table 14.6.1 summarizes the molecularity of elementary reactions.
Table 14.6.1 Common Types of Elementary Reactions and Their Rate Laws
| Elementary Reaction | Molecularity | Rate Law | Reaction Order |
|---|---|---|---|
| A → products | unimolecular | rate = k[A] | first |
| 2A → products | bimolecular | rate = k[A]2 | second |
| A + B → products | bimolecular | rate = k[A][B] | second |
| 2A + B → products | termolecular | rate = k[A]2[B] | third |
| A + B + C → products | termolecular | rate = k[A][B][C] | third |
Multistep Reactions
Most reactions occur in two or more coupled steps,
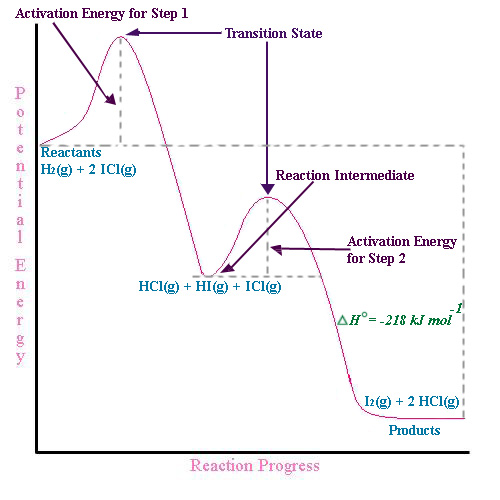
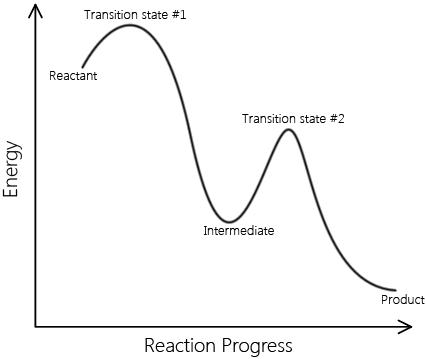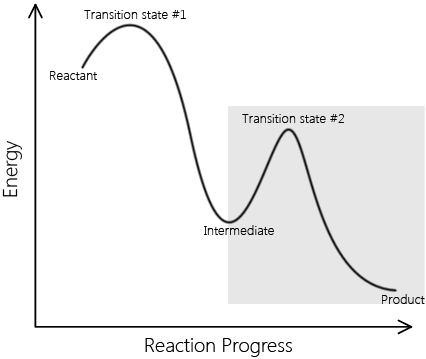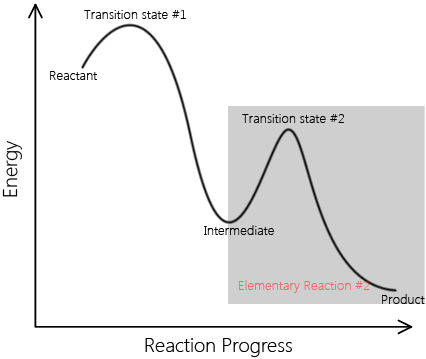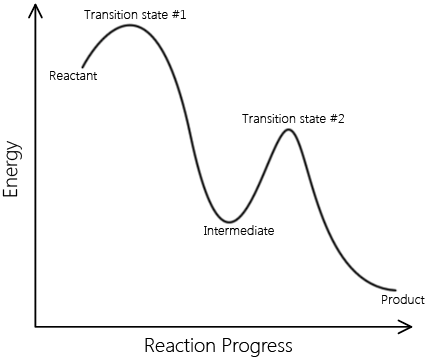
In real mechanisms there can be many intermediates, but to illustrate this we will look at a two step mechanism for the formation of Iodine and Hydrogen chloride gas.
\[H_{2}(g) + 2ICl(g) \rightarrow I_{2}(g) + 2HCl{g} \]
This process occurs in two bimolecular mechanistic (elementary) steps:
\[\begin{align} H_{2} + ICl & \rightarrow HCl + \textcolor{red}{HI} \\ \textcolor{red}{HI} + ICl & \rightarrow HCl + I_{2} \end{align}\]
In the first step HCl and the intermediate HI are formed from the bimolecular reaction of H2 and ICl. In the second elementary step, the HI (intermediate) collides with another ICl in a second bimolecular collision to form HCl and I2. The net result is the reaction
\[H_{2}(g) + 2ICl(g) \rightarrow I_{2}(g) + 2HCl{g}\]
The first two equations (14.6.7 & 14.6.8) are elementary steps of a reaction mechanism and you can determine the rate equation for each step from the stoichiometric coefficients of the elementary steps
R1 = k1[H2][ICl]
R2 = k2[HI][ICl]
Where, k1 & k2 are the rate constants for the first and second steps respectively, and note that the rate equation for the second step has HI in it, which is not a reactant, but an intermediate.
NOTE: Equation 14.6.9 is a balanced chemical equation and not an elementary step of a mechanism, so you can not calculate the order of reactions from its coeficients. What you need to do is run experiments like in section 14.3 of this chapter where you hold hydrogen constant and change the ICl concentration to determine the order of reaction with respect to ICl, and then hold the ICl constant and change the hydrogen concentration to determine the order of reaction with respect to hydrogen.
In the next section we will see that the slow step is the rate determining step, and by comparing the results of experiments on eq. 14.6.9 to the predicted results of 14.6.7 and 14.6.8, we can identify the real mechanism
Mechanisms Based on Rate Determining Step
The observed rate of reaction for a serious of sequentially coupled elementary steps is based on the slow step, otherwise known as the Rate Determining Step.

Rule: In Multi-step Mechanisms the Rate Law is Based on the Elementary Reactions of the Slow Step.
1. First Step Slow Step
When the first step is the slow step the rate law is simple based on the first step, and the subsequent steps (however many) have no effect. Consider a two step mechanism for the following reaction
\[\large NO_{2}+CO \rightarrow NO + CO_{2}\]
Step 1 (Slow): \[\mathrm{NO_2}+\mathrm{NO_2}\xrightarrow{\mathrm{k_1}}\mathrm{NO_3}+\textrm{NO}\]
Step 2 (fast): \[\mathrm{NO_3}+\mathrm{CO}\xrightarrow{k_2}\mathrm{NO_2}+\mathrm{CO_2}\]
The above mechansim would result in an observed rate law based on the slow step:
\[\textrm{rate}_{observed}=k_1[\mathrm{NO_2}]^2\]
Note, the rate law can not be determined from the balanced equation (14.6.10)
2. Second Step Slow Step
Consider the equation
\[\large 2NO + 2H_{2} \rightarrow N_{2} + 2H_{2}O\]
Step 1 (Fast):
\[\mathrm{NO}+\mathrm{NO}\xrightarrow{k_1} \textcolor{red}{\mathrm{N_2O_2}}\]
Step 2 (Slow)
\[\textcolor{red}{\mathrm{N_2O_2}}+\mathrm{H_2}\xrightarrow{k_2} \textcolor{orange}{\mathrm{N_2O}}+\mathrm{H_2O}\]
Step 3 (Fast)
\[\textcolor{orange}{\mathrm{N_2O}}+\mathrm{H_2}\xrightarrow{k_3}\mathrm{N_2}+\mathrm{H_2O}\]
The Rate Law is
\[Rate = k_{2}[\textcolor{red}{N_{2}O_{2}}][H_{2}]\]
But N2O2 is an intermediate!
To solve this problem we are going to assume that the products in the first step can form reactants and reach a psuedostate of equilibrium, that is, their rate of formation equals their rate of dissociation, which is also known as the steady state approximation. So eq14.6.15 can be rewritten as
\[\mathrm{NO}+\mathrm{NO}\underset{k_{-1}}{\stackrel{k_1}{\rightleftharpoons}} \textcolor{red}{\mathrm{N_2O_2}}\]
where k1 is the forward rate constant of the first step, and k-1 is the backward (reverse) rate constant of the first step. The steady state or psuedoequilbrium approximation says that since the second step is so slow, the forward and reverse rate of the first step become equal
\[\begin{align}Rate_{Forward} & =Rate_{Backward} \nonumber \\ \nonumber \\ k_{1}[NO]^{2} & = k_{-1}[\textcolor{red}{N_{2}O_{2}}]\end{align}\]
Solving equation 14.6.20 for N2O2 gives:
\[\textcolor{red}{ [N_{2}O_{2}]}=\frac{k_{1}}{k_{-1}}[NO]^{2}\]
Substituting N2O2 from equation 14.6.21 into equation 14.6.18 gives
\[\begin{align}Rate & = \frac{k_{1}k_{2}}{k_{-1}}[NO]^{2}[H_{2}] \nonumber \\ \nonumber \\ &=k_{obs}[NO]^{2}[H_{2}]\end{align} \]
Note, since the third step was fast, it did not influence the observed rate constant. What the steady state approximation is saying is that the first step rapidly comes to a steady concentration, and we can treat the forward and backward reactions of the first step as if they are at equilibrium. In the next chapter we will look at the behavior of reactions at equilibrium.
In-Class Activity
ADAPT \(\PageIndex{1}\)
Test Yourself
Homework: Section 14.6
Query \(\PageIndex{1}\)
Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:
- Liliane Poirot