11.3: Dipole-Dipole Forces
- Page ID
- 42003
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Dipole–Dipole Interactions
Dipole-Dipole interactions occur between polar molecules. In section 8.8 we learned that polar covalent bonds occur between atoms of different electronegativity (section 8.7), where the more electronegative atom attracts the electrons more than the electropositive atom, and based on the geometry, this may or may not result in a polar molecule. If the center of positive charge (defined by the nuclei) does not coincide with the center of negative charge (defined by the electron orbitals), the molecule is polar, which is easiest to visualize for nonsymmetric orientations of bonds between atoms of different electronegativities. That is, a polar molecule with a permanent dipole results if all the bond dipole vectors add to a net dipole. In this case the molecule's center of positive charge (denoted by δ+) does not coincide with the center of negative charge (denoted by δ-) and the molecular dipole moment (\(\mu\)) is this partial charge times the distance between them. Please review sections 8.7 and 8.8 if needed, and remember that if bond dipoles are of symmetric orientation, like in the linear carbon dioxide, they cancel each other and the molecule is non-polar. So polar bonds can result in non-polar molecules! You should also note that the center of positive charge need not be where there is a nucleus. For example, in water, the center of positive charge is half way between the two hydrogens.
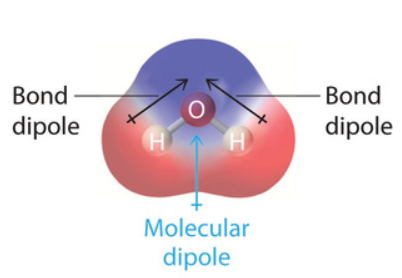
Figure \(\PageIndex{1}\): Water's dipole moment has a positive center between the two nuclei of the hydrogens.
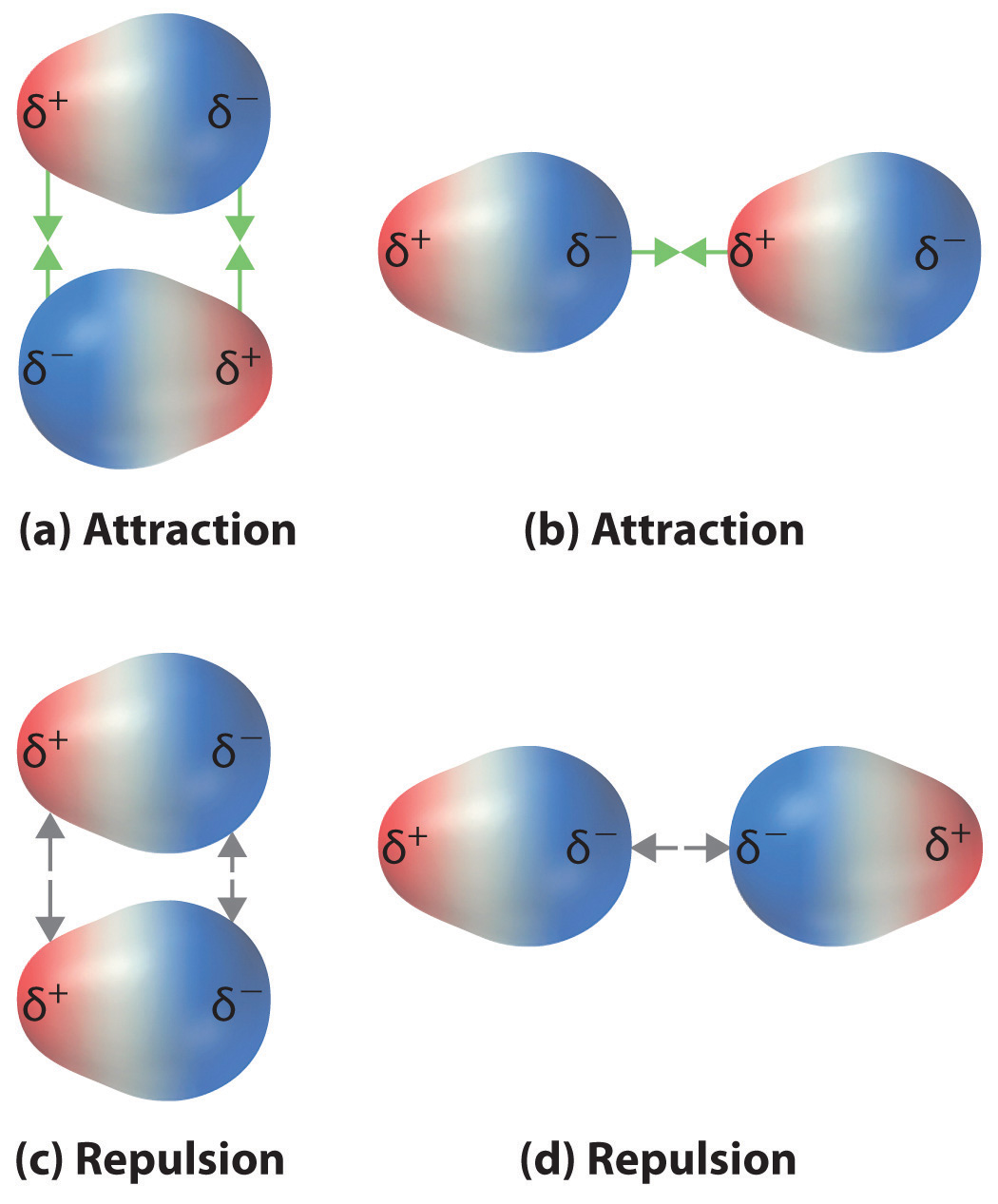
Although molecules in a liquid are in constant motion, they tend to align in the lowest energy orientation, which would be to maximize attractions (parts a & b of fig. 11.3.1) and minimize repulsion (parts c & d of fig. 11.3.1). This follows the same logic we used for ion-dipole interactions, in that the attractive interactions cause dipoles of opposite charge to be closer, resulting in stronger interactions, while dipoles of like charge tend to be farther apart, resulting in reduced interactions. Therefore, unlike ion-ion interactions, but like ion-dipole interactions, dipole-dipole are always attractive.
Exercise \(\PageIndex{1}\)
Why are the attractive forces greater than the repulsive?
- Answer
-
Molecules in a liquid are in constant motion and experience both attractive and repulsive dipole–dipole interactions, as shown in Figure 11.3.2. For reasons similar to those outlined in the section on ion-dipole forces (11.2), the attractive interactions dominate the repulsive because the attraction causes them to be closer together, which increases the Coulombic interactions. Likewise, the repulsions mean they move farther away, which reduces the Coulombic interactions.
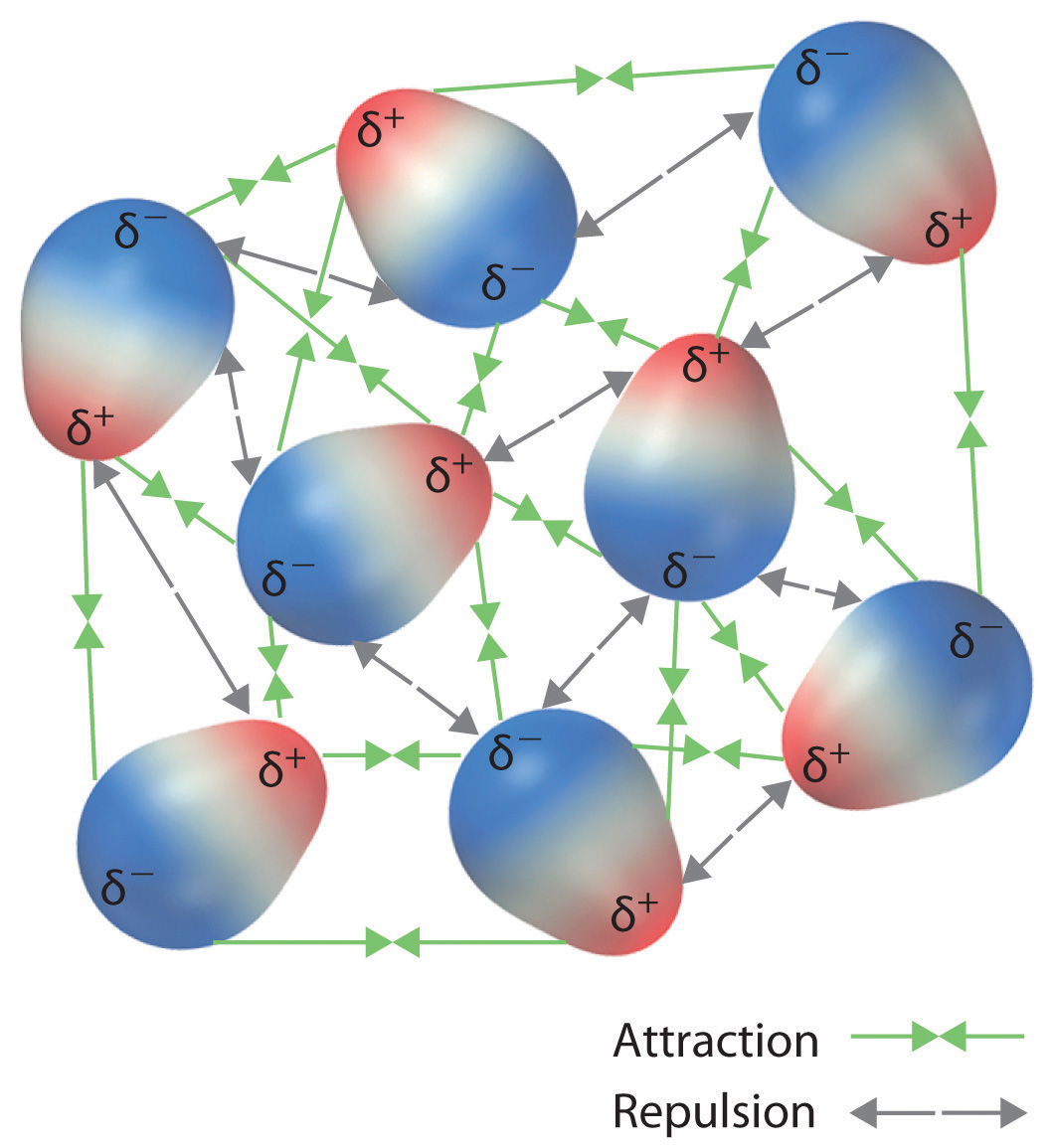
Figure 11.2.2: Both Attractive and Repulsive Dipole–Dipole Interactions Occur in a Liquid Sample with Many Molecules
The equation for dipole-dipole potential energy is
\[\underbrace{E\: \alpha \: \dfrac{-\mu_1\mu_2}{r^3}\\
or \\
E=-k\dfrac{\mu_1\mu_2}{r^3}}_ {\text{ dipole-dipole potential }} \]
This can be compared to eq. 11.2.1 (ion/ion) and 11.2.2 (ion-dipole), and it becomes clear that the dipole-dipole forces are even shorter range. (remember \(\mu\) =qd, where q is the |(δ+/-)| of the dipole, and d is the distance between δ+ and δ−. This is further weaker because the magnitude in the charge is a partial charge and less than 1, while the charge in an ion is +/- 1, 2,3...(an integer multiple of 1).
Note that R is an inverse cube power, and so doubling the distance reduces the energy by a factor of 8. Also note that this is consistent with eq.'s 11.2.2 and 11.2.4 because the term \(mu\) has distance built into it.
Because each end of a dipole possesses only a fraction of the charge of an electron, dipole–dipole interactions are substantially weaker than the interactions between two ions, each of which has a charge of at least ±1, or between a dipole and an ion, in which one of the species has at least a full positive or negative charge.
Exercise \(\PageIndex{2}\)
Show how \(\dfrac{-\mu_1\mu_2}{r^3}\), \(\dfrac{-|q_1|\mu_2}{r^2}\) and \(\dfrac{q_1q_2}{r}\) are dimensionally equivalent?
- Answer
-
\(\dfrac{-\mu_1\mu_2}{r^3}\)=\(\dfrac{(dq_1)(dq_2)}{r^3}\), which has units of \(\dfrac{charge^2}{length}\)
\(\dfrac{-\mu_1|q_2|}{r^2}\)=\(\dfrac{(dq_1)(q_2)}{r^2}\), which has units of \(\dfrac{charge^2}{length)}\)
\(\dfrac{q_1q_2}{r}\), has units of \(\dfrac{charge^2}{length)}\)
In summary, the above relationships show that the attractive interaction between dipoles falls off much more rapidly with increasing distance than do the ion–dipole interactions, which in turn fall off quicker than ion-ion interactions. Doubling the distance (r → 2r) decreases the attractive energy between ions (which is proportional to 1/r) by one-half, which increases ion-dipole by 1/4, that is (1/22), while dipole-dipole interactions decrease to 1/8 (1/23).
Boiling Point Trends
Within a series of compounds of similar molar mass, the strength of the intermolecular interactions increases as the dipole moment of the molecules increases. Using what we learned about predicting relative bond polarities from the electronegativities of the bonded atoms, we can make educated guesses about physical properties that depend on intermolecular forces, like the relative boiling points of similar molecules.
Exercise \(\PageIndex{3}\)
Given the following information:
| Compound | C3H6 (cyclopropane) | CH3OCH3 (dimethyl ether) | CH3CN (acetonitrile) |
|---|---|---|---|
| Structure | |||
| Molar Mass (g/mol) | 42 | 46 | 41 |
(a) Associate the following Dipole Moments with the above compounds: Zero D, 1.30 D and 3.9 D. (Hint: rank in order of increasing polarity)
- Answer
-
Cyclopropane is nonpolar and is zero, dimethyl either is 1.30 and acetonitrile is 3.9. The cyclopropane was a gift, but differentiating the second two is tougher, as oxygen is more electronegative (\(\chi\) = 3.5) then nitrogen (\(\chi\)=3.0), but acetonitrile is linear while dimethyle ether is bent, and part of the two bond dipoles cancel, and the later has a far greater effect (both oxygen and nitrogen are highly electronegative). That is, the dipole for dimethyl ether goes straight up from the oxygen to in between the two carbons, and the horizontal components cancel out. In acetonitrile there is no such cancellation.
(b) Associate the following boiling points with the above compounds: Rank in order of increasing boiling point. 240K, 248K & 355K
- Answer
-
The boiling points follow the trends in the strength of the intermolecular forces, so cyclopropane is 240K, dimethyl ether is 248 and acetonitrile is 355.


